stats + mechanics

P (A / B)

• P (A ∩ B) / P (B)

• [P (B / A) x P (A)] / P (B)

• P (A) , if independent

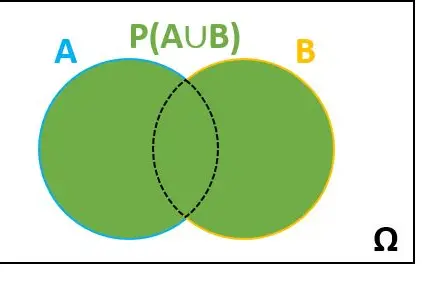
P (A ∪ B)

all of it

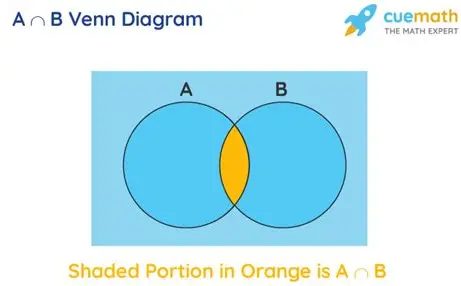
P (A ∩ B)

intersection

mutually exclusive

P (A ∩ B) = 0

independent

P (A) x P (B)

addition law

P (A ∪ B) = [P (A) + P (B)] - P (A ∩ B)

census

measures every member of a population

• + accurate result

• - expensive, testing may destroy

sampling units

individuals of a population

sampling frame

list of sample units

random sampling

1. simple random sampling

   equal change of being selected. uses a random number / lottery system

   • + bias free

   • - needs sampling frame

2. systematic sampling

   take every k^th unit, where k = population / sample. pick a random number between 1 and k to start

   • + quick to start

   • - needs sampling frame

3. stratified sampling

   sample represents groups (strata) of a population. (sample / population) x strata for each strata, and picked randomly

   • + reflects population

   • - population must be classified in strata

non random sampling

1. quota sampling

   like stratified, but strata filled up by interviews / researcher

   • + no sampling frame

   • - non random so potential bias

2. opportunity sampling

   quota filled by who is available at the time

   • + cheap and easy

   • - unlikely to be representative, researcher bias

types of data

qualitive - non numerical

quantitative - numerical

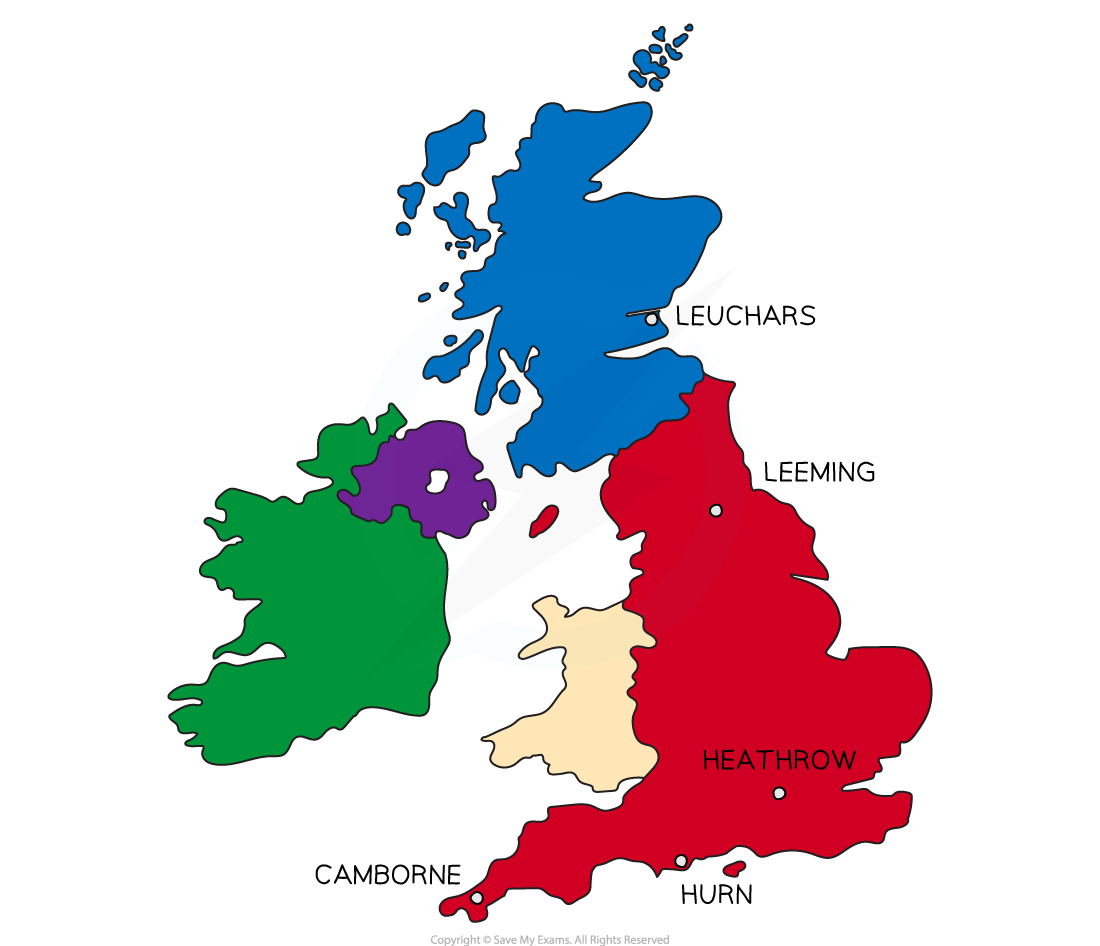
large data set - stations in UK

1. cambourne (coast, south)

2. hurn (coast, south)

3. heathrow (south)

4. leeming (north)

5. leuchars (coast, north)

coastal stations = windy, rainy

south = warmer, more hours in the day

recorded for 6 months only, may - october 1987 - 2015

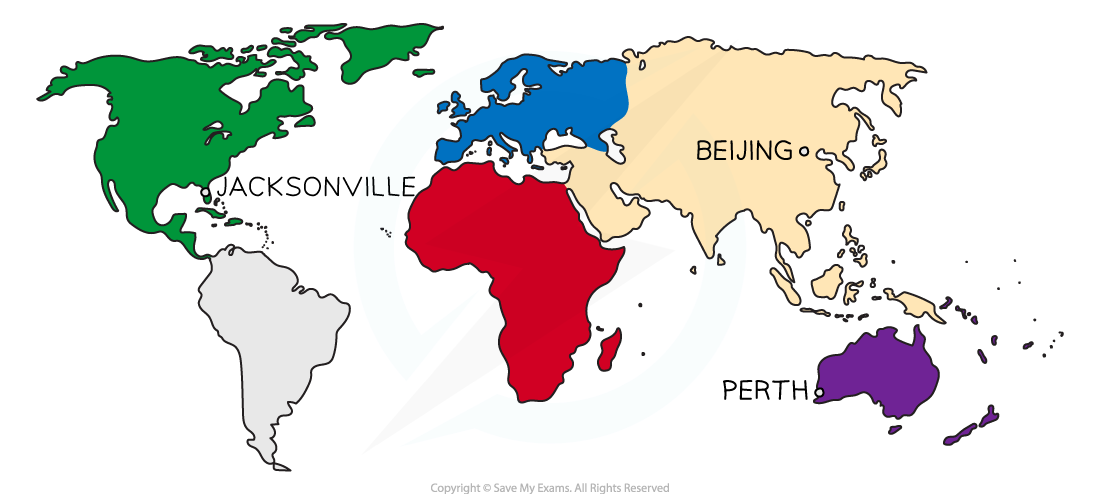
large data set - international stations

1. perth (australia)

   southern hemisphere so seasons switched

   very hot in summer

2. beijing (china)

   really hot and rainy in summer

   really cold in winter

3. jacksonville (florida, usa)

   very warm

   prone to hurricanes

large data set - data

• rainfall

  ‘tr’ means trace, treat it as 0 in calculations

• n/a

  not available, so can’t be used in a sample

• cloud cover

  oktas, discrete values of 0 - 8. measures how many 1/8 of the sky is covered

• max gust

  knots, 1 kn = 1.15 mph

Σ

sum of

measures of location, learn how to do on calc come back

1. measure of central tendency

   • mean

     ^-x = Σx / n

     ^-x of grouped data = Σfx / Σf

   • mode

   • median

2. quartiles

   • for listed data -

     Q₁ = n / 4

     Q₂ = n / 2

     Q₃ = 3n / 4

     where n is the number of sampling units

     if a decimal, round up

     if whole, find midpoint with next number

   • for grouped data -

     Q₁ = n / 4

     Q₂ = n / 2

     Q₃ = 3n / 4

     percentiles , e.g., 57_th = 0.57 x n

     deciles , 10% chunks , e.g., D₃ = P₃₀ = 0.3 x n

     do not round. use linear interpolation

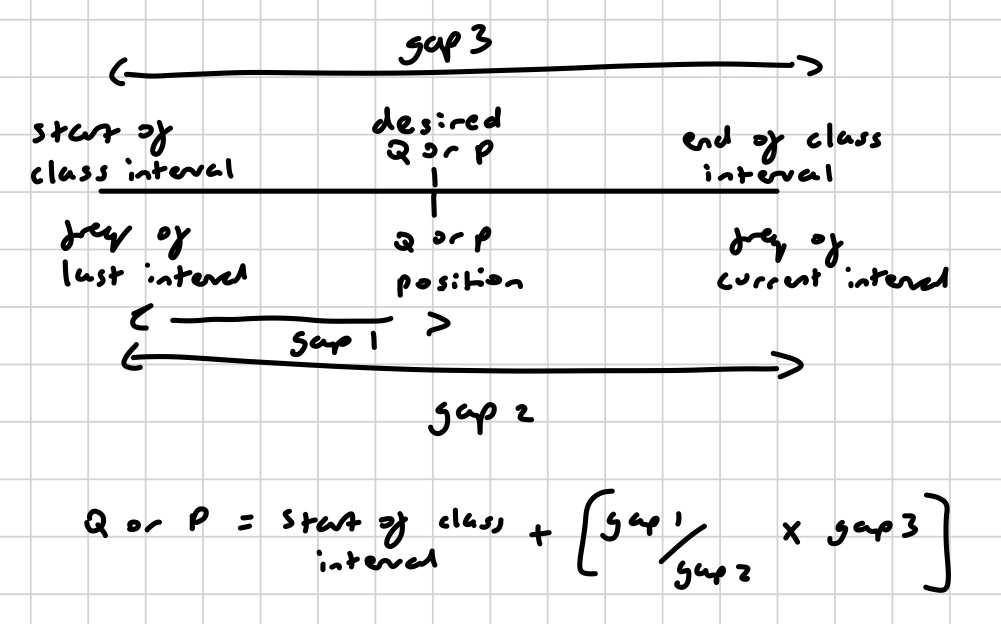
linear interpolation

for grouped data

1. cumulative frequency for quartiles or percentiles

2. find the class interval

measures of spread learn how to do on calc come baxj

1. interquartile range

   IQR = Q₃ - Q₁

   + ignores extremes

2. interpercentile range

   IPR = P_n2 - P_n1

3. variance

σ² = Σ (x - x-)2 / n

or, the mean of the squares [(sum of x2) / n] - square of the mean [x-2]

if it’s frequency data, then σ² = [(sum of fx2) / total frequency] - [fx-2] where fx is data class x frequency. midpoints if continuous

on calc, stats, put into list, calc, 1 var

4. standard deviation

   how much data scatters around the mean on average

   root of the sum of the squared deviations divided by number of values

   σ = _/ (1 / n) x (x1 - x-)2 +(x2 - x-)2 + … + (xn - x-)2

   negative if below the mean, positive if above the mean

   square root of variance equation

coding

if y = ax + b,

then always y^- = ax^- + b

representations of data

1. cumulative frequency

   mark the quartiles on the y-axis and find the corresponding value on the x-axis

2. box plots

   median, LQ, UQ, highest and lowest values, and outliers marked

   can be used to compare location and spread of different data sets

   can be made from a cumulative frequency graph

3. histograms

   for continuous data

   no gaps

   frequency density = freq / class width

   area = freq x k

compare = 1 measure of location, 1 measure of spread

regression and correlation

• product moment correlation coefficient (PMCC)

  -1 ≤ r ≤ 1

  measures strength and + / - of correlation

• regression line

  line of best fit, y = a + b x

  a = y when x = 0

  b = how much y changes when x increases by 1

• interpolation = estimating inside the data range

  more reliable

• extrapolation = estimating outside the data range

  not reliable

• if y = ab^x , exponential

  log y = log a + x log b

  y = c + m x

  (m = log b, x = x)

• if y = axⁿ , polynomial

  log y = log a + n log x

  y = c + m x

  (m = n, x = log x)

discrete uniform distribution

probabilities of outcomes are all equal

mean is in the middle, and is the same as the median, = (a + b) / 2

all value add up to 1

standard deviation = _/ (b - a)2 / 12

probability questions usually finding an interval. all probability the same, so find as ratio (d - c) / (b - a)

hypothesis testing

binomial distribution

normal distribution

outliers

> Q₃ + k IQR

< Q₁ - k IQR

measures of central tendency on grouped data

mean

1. midpoints of class

2. [sum of midpoints x frequency of class] / total frequency

median

1. total frequency (n) / 2

2. cumulative frequency to find which class the n / 2 is in

3. linear interpolation

mode

1. class with the highest frequency