COMP306 #13 Tree Based Indexing

example ISAM Tree

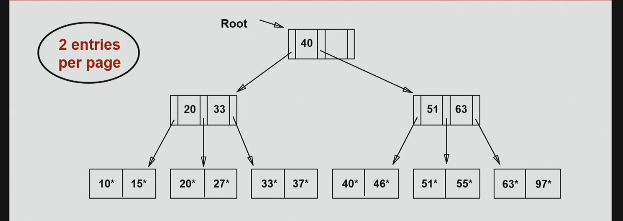
structure of leag pages

only store data entries

structure of non-leaf pages:

pointers and keys.

non-leaf pages are

static

two types of leaf pages

primary pages and overflow pages

non-leaf pages act as

guides

leaf pages store

actual data entires

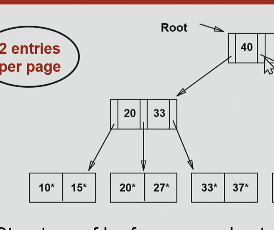
40 pointer meaning here

everything will be less than 40.

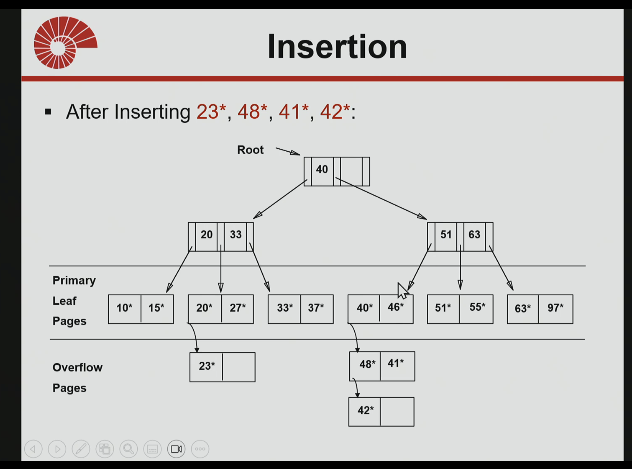
insertion into an isam tree

find where 23 belongs, start at the node, then 23 is between 20 and 33, then follow that pointer, but guess what the page is full, so create an overflow page,

deletion example

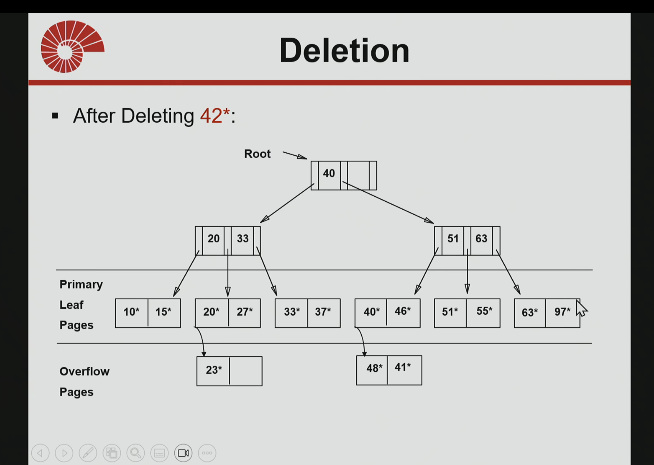
find 42 in the tree, delete it

why isam tree a static data strucutre?

because non-leaf pages don’t change (leaf pages and overflow pages might change).

what is the problem with static isam trees

the complexity is dependent on the insertion deletion order, initally it can be quite balanced but later on it might get shitty. long overflow chains (straight up linked list mate)

best case worst case complexities in an ISAM tree

O(logN), N.

B+ tree

self-balancing tree data strucutre that keeps data sorted and allows search sequential access, insertion and deletion in O(logN) time. commonly used in today’s DBMS

properties of B+ trees

perfectly height balanced at all timese
every node other than the root must be atleast half full
order = m means nodes have at most m children (thus each node holds at most m-1 data entrires)

example b+ tree

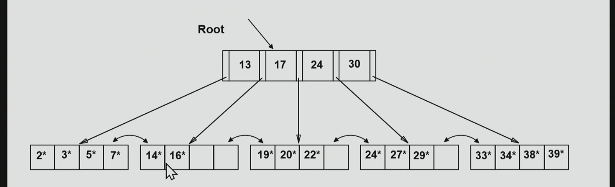
notice that there are pointers between leaf nodes.

the benefit of having pointers between leaf nodes

sequential thing:

i.e. we want to look at 24 first, then we scan to the right.

insertion in B+ trees

find the leaf node L to insert to

if L has enogh space: insert into L, ensure the leaf is sorted done! (since we can serach in the leaf nodes thats why they should be sorted.)

otherwise:
must split L into two nodes
redistribute entries evenly, copy up the middle key. this split may cause recurisve splits in the upper levels

to handle splits in the upper levels: redistribute entries evenly, push up the middle key
always check if the push up causes further splits.

inserting 8 into this tree

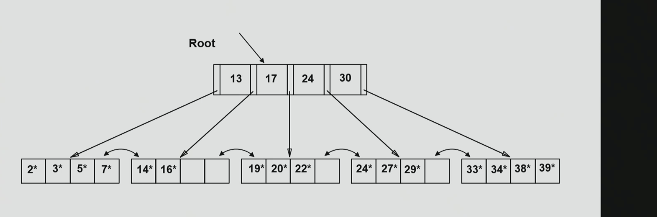
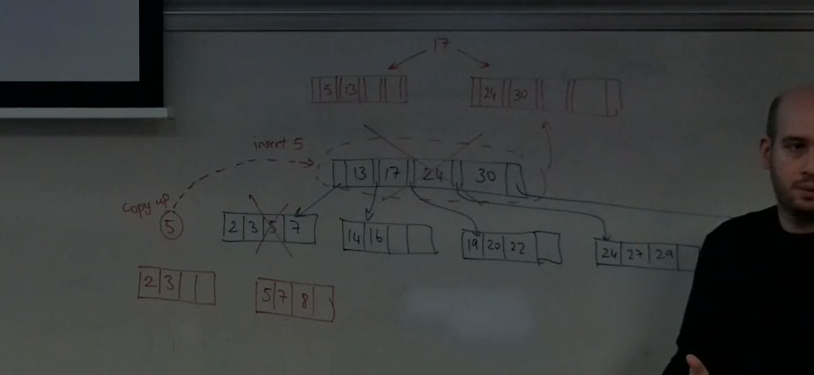
don’t forget the importance of pushing up vs copying up.

deletion in a B+ tree

start at the root, find leaf L where entry resides.

remove the entry from L

after remove if L is at least half full, done!

otherwise, try to redistribute by borrwon from L’s right sibling adjacent node with same parent as L
if re-distribution fails, merge L and its sibling

if merge occurs, we must delete the entry seperating L and its sibling from L’s parent

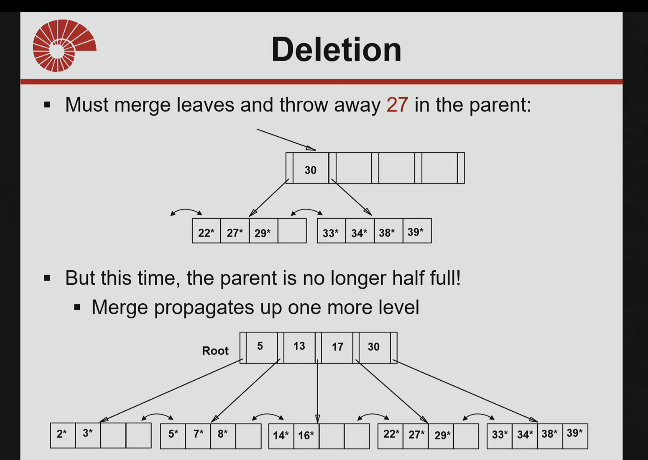
merge could propogate all the way up to the root and cause decreased tree height.

deletion example

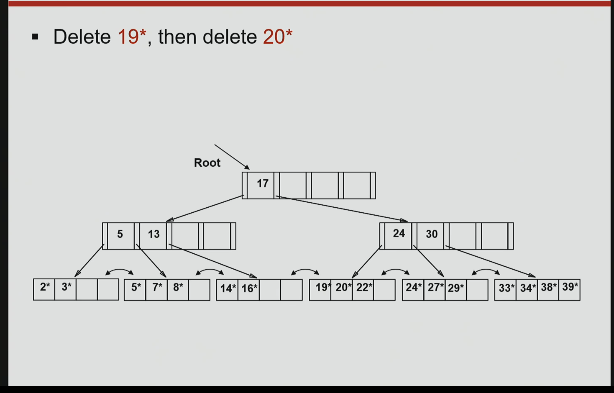
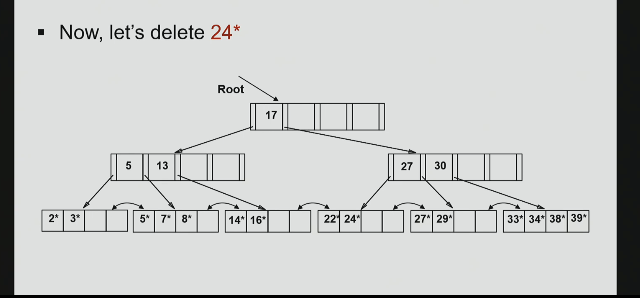
should merge these cunts now.

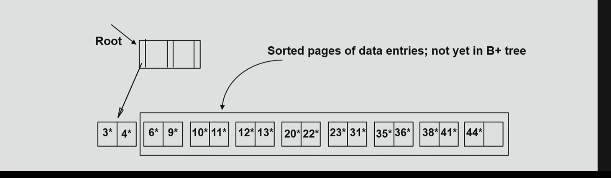
bulk loading

if we have a large collection of records and we want to create a B+ tree with them, doing so by repeatedly inserting records in random order can be slow

can be solved by bulk loading of the B+ tree

sort all records, initalize empty root and start adding.

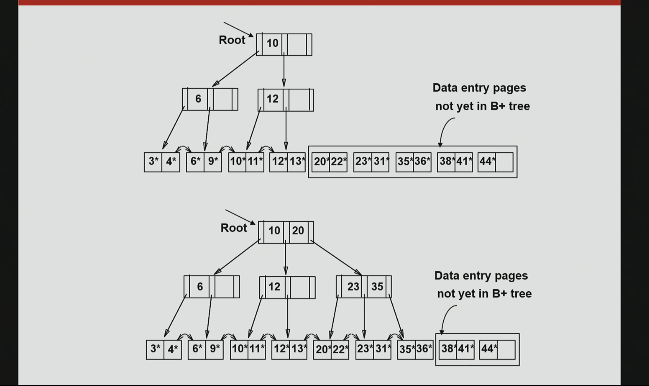
why: the left part of the B+ tree is not changing whatsoever (,ajority of the tree never changes).