Week 3 Lecture 2 - Do Regular Expressions describe the same language as Finite Automata?

What are regular expressions?

Patterns which describe languages. They are commonly found in string processing systems, where they may be thought as patterns or shorthands

What are regular expressions built from?

1. Constants describing simple languages

2. Language operations (combinators) to build up more complicated language.

Given an alphabet Σ, how are the regular expressions Σ inductively defined?

1. ∅, λ and, for each a ∈ Σ, a are regular expressions

2. If E and F are regular expressions then so are E + F , EF , E* and (E )

Given a regular expression E over Σ, the language L(E ) denoted by E is inductively defined as follows (write the equivalence):
L(∅)
L(λ)
For each a ∈ Σ, L(a)
L((E))
L(EF)
L(E*)
L(E + F)

L(∅) = ∅
L(λ) = {λ}
For each a ∈ Σ, L(a) = {a}
L((E)) = L(E)
L(EF) = L(E)L(F)
L(E*) = (L(E))*
L(E + F) = L(E) ∪ L(F)

Precedence in regular expressions:

1. Brackets have the highest precedence

2. The star operator has the second highest precedence

3. Concatenation has the third highest precedence

4. Union (+) has the lowest precedence

5. Consecutive concatenation or unions are grouped from the left (left-associative)

Using precedence, what do each of these regular expressions stand for?

1+01*

010

0+1+0

1+01* → 1+(0(1*))

010 → (01)0

0+1+0 → (0+1)+0

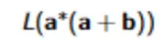
Convert this regular expression to a regular language

The language consists of all strings with 0 or more symbols, followed by either an a or a b

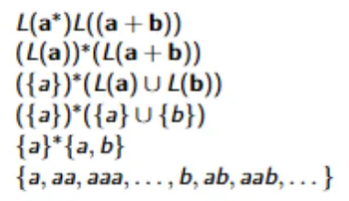
Convert all of these regular languages to regular expressions

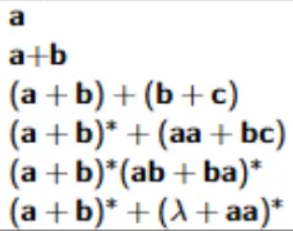
Consider L = {w ∈ {0, 1}∗ | w has no pair of consecutive 0s}.

Convert this to a regular expression, with all of the steps and other ways it can be denoted

In other words whenever 0 occurs it must immediately be followed by at least one 1. Part of this can be achieved by the regular expression (011)**.

But more is needed: there may be a 0 at the end, and the string could start with 1 or more 1s.

We need 1(011)*(0 + λ)**

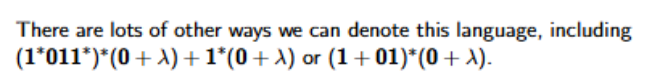
How can

→ 1 or more (a)

→ n or more (a)

→ 0 or 1 (a)

Be written as in regular expressions

→ 1 or more (a) can be written as aa*

→ n or more (a) can be written as aaaaaaaa* (for 7 or more)

→ 0 or 1 (a) can be written as a + λ

Prove the claim: the set of languages that can be denoted by regular expressions is exactly the same as the set of regular languages

By definition, a language is regular if and only if it is accepted by some FSA.

Therefore, the claim is true if and only if the set of languages that can be denoted by regular expressions is exactly the same as the set of languages that can be accepted by FSAs.

Prove: Every regular expression denotes a language that can be accepted by some FSA.

Prove: Every language that is accepted by an FSA can be denoted by some regular expression

What is a Generalised Non-Deterministic Finite State Automata (GNFAs)

Transition diagrams have arcs labelled with regular expressions. A path from the initial state to an accepting state represents the language obtained by concatenating the languages of the expressions along the path. The language accepted by a GNFA is the union of the languages represented by all paths from the initial state to an accepting state.

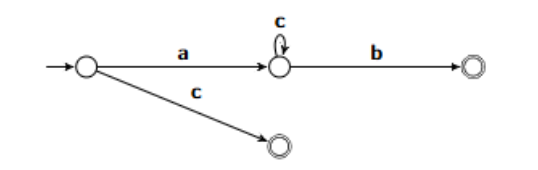
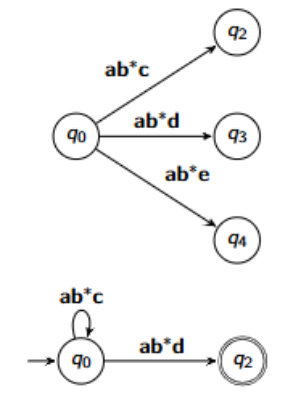
What is the GNFA for this NDFA?

a → b = ab
a → c (self loop) → b = ac*b
adding on the a → c:
ac*b + c

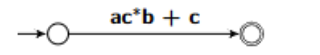
How do you convert any NDFA to an equivalent GNFA?

→ Turn each symbol a into a regular expression a.
→ Turn each λ-transition into a transition labelled with the regular expression λ. Without the loss of generality, we can assume that GNFAs have a single final state. → Otherwise, change each final state into a non-final state.
→ Create a transition labelled with λ from each original final state to a new unique final state.

Without loss of generality, we can also assume that GNFAs have at most one transition from any state q to any other state p, and at most one transition from q to itself.

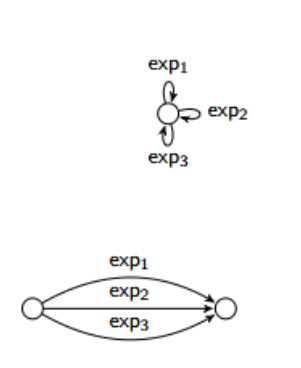
What are the reduction rules for removing parallel arcs in an GNFA?

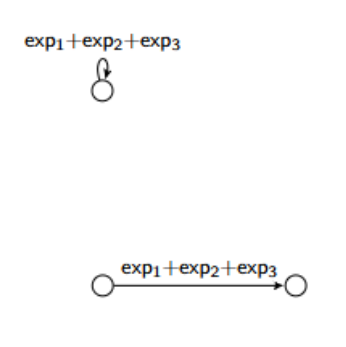
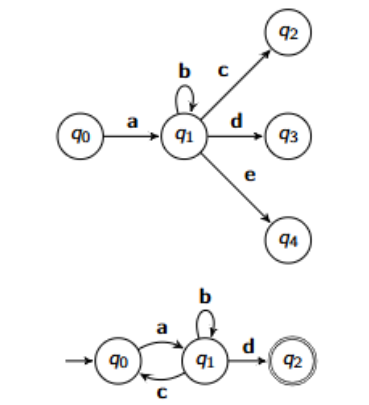
Give the reduction for this NDFAs: