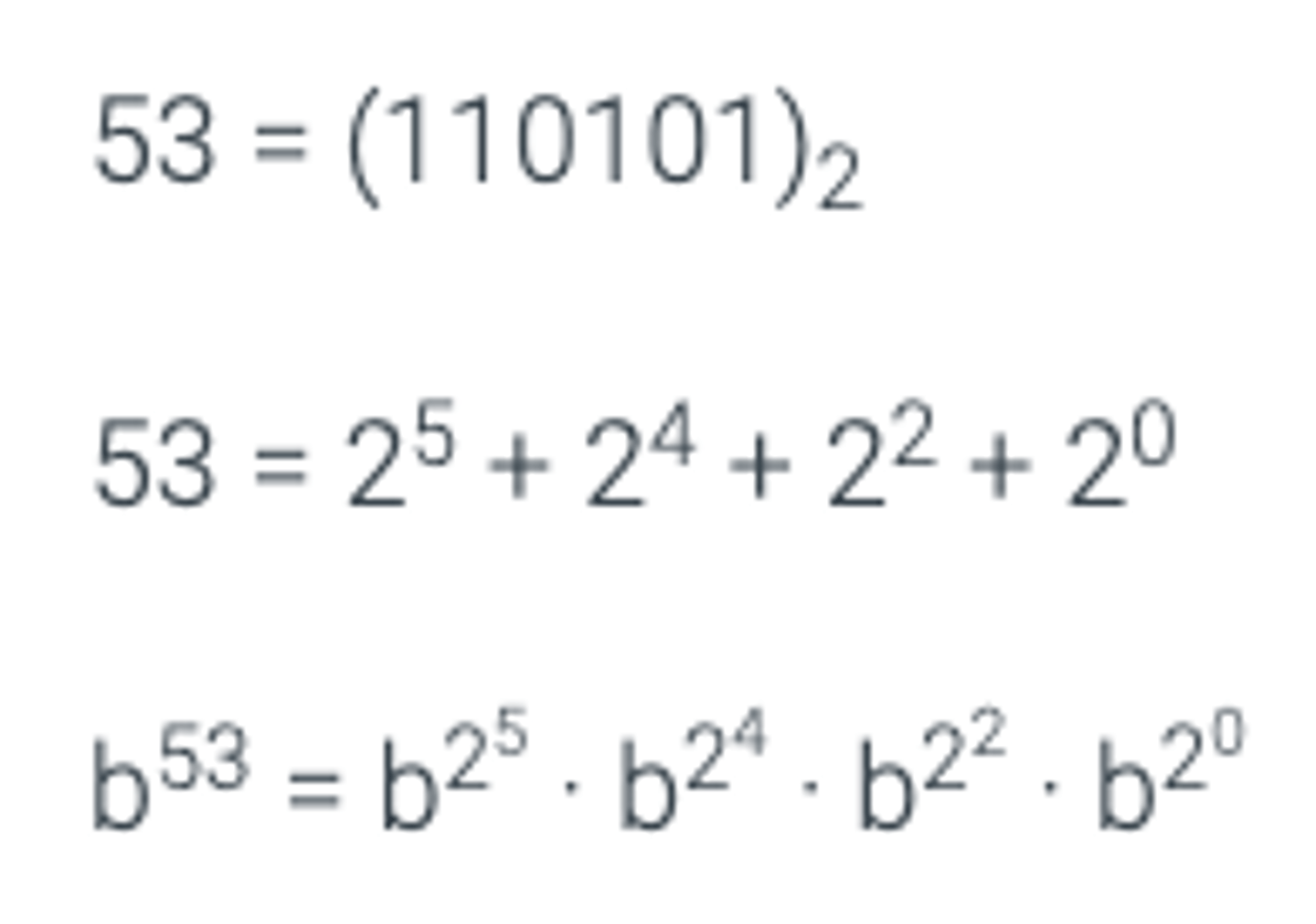C960 Discrete Math 2

1.4.3: If-else-statement

1)

What is the value of abs after the following lines of code are run?

x := 2

If ( x > 0 )

abs := x

Else abs := -x

End-if

2

The condition ( x > 0 ) evaluates to true because the value of x is 2. The line abs := x is executed and the line abs := -x is skipped. Therefore the final value of abs is 2.

1.4.3: If-else-statement

2)

What is the value of abs after the following lines of code are run?

x := -2

If ( x > 0 )

abs := x

Else

abs := -x

End-if

2

The condition ( x > 0 ) evaluates to false because the value of x is -2. The line abs := x is skipped and the line abs := -x is executed. Therefore the final value of abs is -x, which is -(-2) = 2.

1.5.2: For-loops

Consider the following pseudocode fragment:

sum := 0

For i = 2 to 5

sum := sum + i

End-for

1) What is the value of sum after the second iteration?

2) How many iterations will the for-loop execute?

3) What is the final value for sum after executing the for-loop?

1) 5

In the first iteration, i = 2. In the second iteration, i = 3. 2 + 3 = 5

2) 4

i = 2, 3, 4, 5. Four iterations

3) 14

i = 2, 3, 4, 5. sum = 2 + 3 + 4 + 5

1.6.2: While-loops

product := 1

count := 5

While ( count > 0 )

product := product⋅count

count := count - 2

End-while

1) What is the value of product after the second iteration?

2) How many iterations will the while-loop execute?

3) What is the final value for product?

1) 15

In the first iteration, count = 5. In the second iteration, count = 3. 5⋅3 = 15

2) 3

count = 5, 3, 1. Three iterations

3) 15

product = 5⋅3⋅1 = 15

1.7.2: Nested loops - example 1

count := 0

For i = 1 to 3

For j = 1 to 4

count := count + i ⋅ j

End-for

End-for

1) How many times is the variable count increased?

2) What is the final value of count?

1) 12

For each iteration of the outer loop, the inner loop iterates 4 times. The outer loop iterates 3 times. 3 × 4 = 12

2) 60

1·(1 + 2 + 3 + 4) + 2(1 + 2 + 3 + 4) + 3(1 + 2 + 3 + 4) = 60

1.7.3: Nested loops - example 2

Consider the following pseudocode fragment:

count := 0

For i = 1 to 3

For j = i+1 to 4

count := count + i ⋅ j

End-for

End-for

1) When i = 2, how many times does the inner loop iterate?

2) How many times is the variable count increased?

3) What is the final value of count?

1) 2

The initial value of j is i + 1. The final value of j is 4. j = 3, 4. 2 iterations.

2) 6

When i = 1, j = 2, 3, 4. When i = 2, j = 3, 4. When i = 3, j = 4. A total of 6 iterations.

3) 35

1·(2 + 3 + 4) + 2·(3 + 4) + 3·(4) = 35

Exercise 1.7.1: Writing algorithms in pseudocode.

Write an algorithm in pseudocode for each description of the input and output.

(a)

Input: a1, a2,...,an, a sequence of numbers, where n ≥ 1n, the length of the sequence.Output: "True" if the sequence is non-decreasing and "False" otherwise.

A sequence of numbers is non-decreasing if each number is at least as large as the one before.

Exercise 1.7.1: Writing algorithms in pseudocode.

Write an algorithm in pseudocode for each description of the input and output.

b)

Input: a1, a2,...,an, a sequence of numbers, where n ≥ 1 n, the length of the sequence.

Output: "True" if there are two consecutive numbers in the sequence that are the same and "False" otherwise.

Exercise 1.7.1: Writing algorithms in pseudocode.

Write an algorithm in pseudocode for each description of the input and output.

c)

Input: a1, a2,...,an, a sequence of numbers, where n ≥ 1 n, the length of the sequence.

Output: "True" if there are any two numbers in the sequence whose sum is 0 and "False" otherwise.

Exercise 1.7.1: Writing algorithms in pseudocode.

Write an algorithm in pseudocode for each description of the input and output.

d)

Input: a1, a2,...,an, a sequence of numbers, where n ≥ 1n, the length of the sequence.

Output: "True" if there are any three numbers in the sequence that form a Pythagorean triple.

The numbers x, y, and z are a Pythagorean triple if x2 + y2 = z2.

Exercise 1.7.1: Writing algorithms in pseudocode.

Write an algorithm in pseudocode for each description of the input and output.

e)

Input: a1, a2,...,an, a sequence of distinct numbers, where n ≥ 2 n, the length of the sequence.

Output: The second smallest number in the sequence.

1.13.1: Asymptotic growth

Find the asymptotic behavior for the given functions by dropping the constant factors and by keeping the terms that grow the fastest. Type exponents as: ^# Ex: n^2

1) f(n) = 5n + 12

n

Drop the term 12 and the constant multiplier 5.

1.13.1: Asymptotic growth

Find the asymptotic behavior for the given functions by dropping the constant factors and by keeping the terms that grow the fastest. Type exponents as: ^# Ex: n^2

2) f(n) = 109

1

In this example 109 is the constant multiplier of 1. Drop the multiplier 109, but keep the 1 to indicate that this function has a non-zero value.

1.13.1: Asymptotic growth

Find the asymptotic behavior for the given functions by dropping the constant factors and by keeping the terms that grow the fastest. Type exponents as: ^# Ex: n^2

3) f(n) = n^2 + 3n + 112

n^2

In this example n^2 grows larger than 3n for sufficiently large n, so the n^2 term impacts the growth of the function the most as n grows.

1.13.1: Asymptotic growth

Find the asymptotic behavior for the given functions by dropping the constant factors and by keeping the terms that grow the fastest. Type exponents as: ^# Ex: n^2

4) f(n) = n^3 + 1999n + 1337

n^3

Even though the constant factor in front of n(1999) is quite large, you can still find a large enough n so that n^3 is bigger than 1999n. As you are interested in the behavior for very large values of n, you only keep n^3.

Tip: If you cannot readily decide which one of the terms grows faster, plug in several large values for n and compare.

1.13.1: Asymptotic growth

Find the asymptotic behavior for the given functions by dropping the constant factors and by keeping the terms that grow the fastest. Type exponents as: ^# Ex: n^2

5) f(n) = n + squareroot(n)

n

In this example, n grows faster than \sqrt{n} as n increases.

Exercise 1.13.1: Asymptotic function

a) f(n) = n^6 + 3n

n^6

Exercise 1.13.1: Asymptotic function

b) f(n) = 2^n + 12

2^n

Exercise 1.13.1: Asymptotic function

c) f(n) = 3^n + 2^n

3^n

Exercise 1.13.1: Asymptotic function

d) f(n) = n^n + n

n^n

1.14.1: Big-O

True or False

1) A Θ (n) algorithm is O (n)

True

This is as true as our original program was theta (n). You can achieve big O (n) without altering your program at all.

1.14.1: Big-O

True or False

2) A Θ (n) algorithm is O (n^2).

True

As n^2 is worse than n, this is true.

1.14.1: Big-O

True or False

3) A Θ (n^2) algorithm is O (n^3).

True

As n^3 is worse than n^2, this is true.

1.14.1: Big-O

True or False

4) A Θ (n) algorithm is O (1).

False

As 1 is not worse than n, this is false. If a program takes n instructions asymptotically (a linear number of instructions), you cannot make it worse and have it take only 1 instruction asymptotically (a constant number of instructions).

1.14.1: Big-O

True or False

5) A O (1) algorithm is Θ (1).

True

This is as true as the two complexities are the same.

1.14.1: Big-O

True or False

6) A O (n) algorithm is Θ (1).

This may or may not be true depending on the algorithm. In the general case it is false. If an algorithm is Θ(1), then it certainly is O(n). But if it is O(n) then it may not be Θ(1). For example, a Θ(n) algorithm is O(n) but not Θ(1).

2.3.1: Integer divisibility

Yes or No

1) Does 7 divide 56?

Yes

56 = 7·8. 56 is an integer multiple of 7.

2.3.1: Integer divisibility

Yes or No

2) 7·18 + 14·17 = 364.

Does 7 divide 364?

Yes

364 is a linear combination of 7 and 14. 7 divides both 7 and 14.

2.3.1: Integer divisibility

Yes or No

3) Does 8 divide 99?

No

There is no integer k such that 99 = 8k

2.3.3: Computing div and mod

Compute the following value:

1) 17 mod 6

5

The answer is the remainder of 17 divided by 6.

17 = 2 · 6 + 5

2.3.3: Computing div and mod

Compute the following value:

2) 23 div 5

4

Starting with 23, 5 can be subtracted 4 times until the result yields a number in the range from 0 through 4.

23 - 4 · 5 = 3

23 = 4 · 5 + 3

2.3.3: Computing div and mod

Compute the following value:

3) -10 mod 5

0

Starting with -10, when 5 is added 2 times to -10, the result is 0, which is in the range from 0 through 4.

-10 + 2 · 5 = 0

-10 = -2 · 5 + 0

2.3.3: Computing div and mod

Compute the following value:

4) -13 div 6

5

Starting with -13, when 6 is added 3 times to -13, the result is 5, which is in the range from 0 through 5.

-13 + 3 · 6 = 5

-13 = -3 · 6 + 5

2.3.3: Computing div and mod

Compute the following value:

5) -13 div 6

-3

Starting with -13, 6 is added 3 times until the result yields a number in the range from 0 through 5.

-13 + 3 · 6 = 5

-13 = -3 · 6 + 5

Exercise 2.3.1: Computing div and mod

Compute the value of the following expressions:

a) 344 mod 5

344 = 68·5 + 4, so 344 mod 5 = 4.

Exercise 2.3.1: Computing div and mod

Compute the value of the following expressions:

b) 344 div 5

344 = 68·5 + 4, so 344 div 5 = 68

Exercise 2.3.1: Computing div and mod

Compute the value of the following expressions:

c) -344 mod 5

(−344) = (−69)·5 + 1, so (−344) mod 5 = 1.

Exercise 2.3.1: Computing div and mod

Compute the value of the following expressions:

d) -344 div 5

(−344) = (−69)·5 + 1, so (−344) div 5 = −69.

Exercise 2.3.1: Computing div and mod

Compute the value of the following expressions:

e) 215 mod 7

215 = 30·7 + 5, so 215 mod 7 = 5.

Exercise 2.3.1: Computing div and mod

Compute the value of the following expressions:

f) 215 div 7

215 = 30·7 + 5, so 215 div 7 = 30.

Exercise 2.3.1: Computing div and mod

Compute the value of the following expressions:

g) -215 mod 7

(−215) = (−31)·7 + 2, so (−215) mod 7 = 2.

Exercise 2.3.1: Computing div and mod

Compute the value of the following expressions:

h) -215 div 7

(−215) = (−31)·7 + 2, so (−215) div 7 = −31.

2.4.1: Arithmetic for integers modulo n

1) What is the value of (6 + 8) mod 4?

2

(6 + 8) mod 4 = 14 mod 4 = 2

2.4.1: Arithmetic for integers modulo n

2) What is the value of 5 * 7 mod 9?

8

5·7 mod 9 = 35 mod 9 = 8

2.4.1: Arithmetic for integers modulo n

3) What is the value of 4 * 9 mod 6?

0

4·9 mod 6 = 36 mod 6 = 0

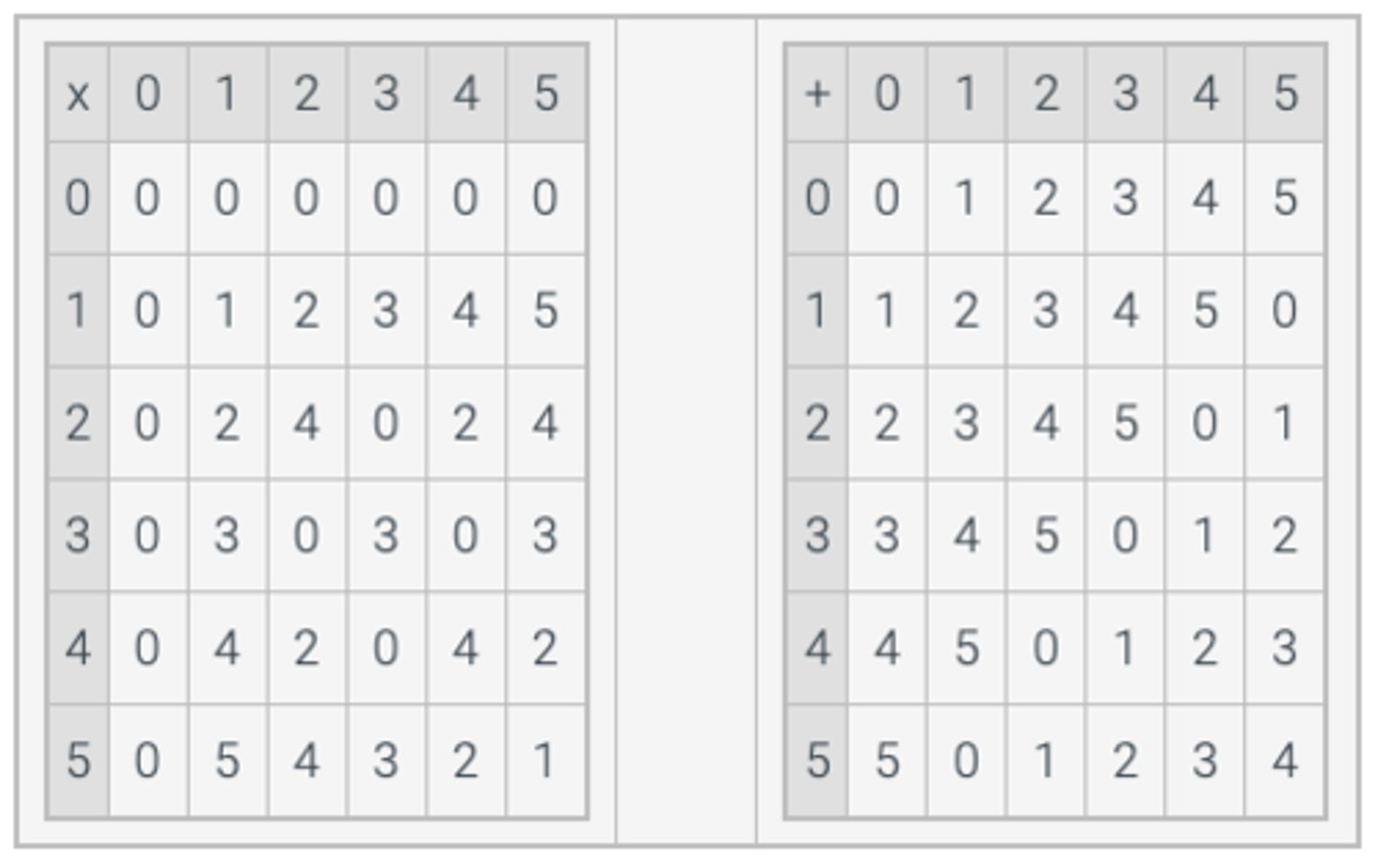
Exercise 2.4.1: Tables for multiplication and addition modulo 6.

(a) Give the tables for multiplication and addition modulo 6.

2.5.3: Computing arithmetic expressions modulo n.

Give an integer value for the following expressions. You should not need a calculator.

1) (651^23 + 17) mod 10

Exercise 2.5.1: Computing using modular arithmetic.

Compute the value of the following expression:

a) 38^7 mod 3

38^7 mod 3 = (38 mod 3)^7 mod 3 = (2^7) mod 3 = 128 mod 3 = 2

Exercise 2.5.1: Computing using modular arithmetic.

Compute the value of the following expression:

b) (72 · (−65) + 211) mod 7

(72 · (−65) + 211) mod 7 = ((72 mod 7) · (−65 mod 7) + (211 mod 7)) mod 7 =

(2 · 5 + 1) mod 7 = 11 mod 7 = 4

Exercise 2.5.1: Computing using modular arithmetic.

Compute the value of the following expression:

c) (77 · (−65) + 147) mod 7

(77 · (−65) + 147) mod 7 = ((77 mod 7) · (−65) + (147 mod 7)) mod 7 =

(0 · (−65) + 0) mod 7 = 0

Exercise 2.5.1: Computing using modular arithmetic.

Compute the value of the following expression:

d) 44^12 mod 6

44^12 mod 6 = (44 mod 6)^12 mod 6 = 2^12 mod 6 = (2^6 mod 6)(2^6 mod 6) mod 6 =

(64 mod 6)(64 mod 6) mod 6 = 4 · 4 mod 6 = 16 mod 6 = 4

Exercise 2.5.1: Computing using modular arithmetic.

Compute the value of the following expression:

e) 17^12 mod 3

17^12 mod 3 = (17 mod 3)^12 mod 3 = 2^12 mod 3 = (2^6 mod 3)(2^6 mod 3) mod 3 =

(64 mod 3)(64 mod 3) mod 3 = 1 · 1 mod 3 = 1

Exercise 2.5.2: Congruence modulo n

a) Group the numbers from the given set into classes of congruence. That is, put two numbers in the same group if they are equivalent modulo 11.

{−57, 17, 108, 0, −110, −93, 1111, 130, 232}

Congruent to 0 modulo 11: 0, -110, 1111

Congruent to 1 modulo 11: 232

Congruent to 6 modulo 11: 17, -93

Congruent to 9 modulo 11: -57, 108, 130

Exercise 2.5.2: Congruence modulo n

b) Group the numbers from the given set into classes of congruence. That is, put two numbers in the same group if they are equivalent modulo 13.

{−63, -54, -41, 11, 13, 76, 80, 130, 132, 137}

Congruent to 0 modulo 13: 13, 130

Congruent to 2 modulo 13: -63, 80, 132

Congruent to 7 modulo 13: 137

Congruent to 11 modulo 13: -54, -41, 11, 76

2.7.1: Prime factorizations

Select the correct choice

1) Which of the following is the prime factorization for 48?

- 3 * 4^2

- 2^4 * 3

- 2 * 3^2

2^4 * 3 = 48. Also, 2 and 3 are both prime numbers.

2.7.1: Prime factorizations

Select the correct choice

2) What is the prime factorization for 31?

- 31

- 1 * 31

- 3 * 13

31 is a prime number, so its prime factorization is itself.

2.7.1: Prime factorizations

Select the correct choice

3) In which prime factorization are the prime factors listed in non-decreasing order?

- 2 7 13 * 11

- 2 7 11 * 13

- 7 2 11 * 13

Each prime factor is greater than or equal to the one that precedes it.

Exercise 2.8.1: Computing using prime factorizations.

Some numbers and their prime factorizations are given below.

140 = 2^2 · 5 · 7

175 = 5^2 · 7

532 = 2^2 · 7 · 19

648 = 2^3 · 3^4

1078 = 2 · 7^2 · 11

1083 = 3 · 19^2

15435 = 3^2 · 5 · 7^3

25480 = 2^3 · 5 · 7^2 ·13

Use these prime factorizations to compute the following quantities.

a) gcd(1078, 25480)

2 * 7^2 = 98

Exercise 2.8.1: Computing using prime factorizations.

Some numbers and their prime factorizations are given below.

140 = 2^2 · 5 · 7

175 = 5^2 · 7

532 = 2^2 · 7 · 19

648 = 2^3 · 3^4

1078 = 2 · 7^2 · 11

1083 = 3 · 19^2

15435 = 3^2 · 5 · 7^3

25480 = 2^3 · 5 · 7^2 ·13

Use these prime factorizations to compute the following quantities.

b) lcm(175, 25480)

2^3 5^2 7^2 * 13 = 127400

Exercise 2.8.1: Computing using prime factorizations.

Some numbers and their prime factorizations are given below.

140 = 2^2 · 5 · 7

175 = 5^2 · 7

532 = 2^2 · 7 · 19

648 = 2^3 · 3^4

1078 = 2 · 7^2 · 11

1083 = 3 · 19^2

15435 = 3^2 · 5 · 7^3

25480 = 2^3 · 5 · 7^2 ·13

Use these prime factorizations to compute the following quantities.

c) 175 * 25480

2^3 5^3 7^3 * 13 = 4459000

Exercise 2.8.1: Computing using prime factorizations.

Some numbers and their prime factorizations are given below.

140 = 2^2 · 5 · 7

175 = 5^2 · 7

532 = 2^2 · 7 · 19

648 = 2^3 · 3^4

1078 = 2 · 7^2 · 11

1083 = 3 · 19^2

15435 = 3^2 · 5 · 7^3

25480 = 2^3 · 5 · 7^2 ·13

Use these prime factorizations to compute the following quantities.

d) 25480/140

2 7 13 = 182

2.9.1: Brute force factoring.

1) Suppose that the slightly better brute force algorithm for factoring is given the number 653117 as input. How many numbers would the algorithm have to check to either find a factor or determine that the input is prime? (653117 happens to be a prime number).

808

234497

19

808

The algorithm can stop checking numbers when it reaches x=⌊squareroot (653117)⌋= 808. Since 653117 is prime, the algorithm will not find a factor before reaching x = 808.

2.9.2: Finding a random number

Use a calculator for this question if needed.

1) Consider a random integer selected from the range from 2 to 1,000,000,000,000. Approximately, what are the chances that the selected number is prime?

0.0032

0.312

0.036

The chances the selected number is prime is 1/ln(1,000,000,000,000) which is approximately 0.036.

Exercise 2.9.1: Estimating the number of primes.

(a) Use the prime number theorem to give an approximation for the number of prime numbers in the range 2 through 10,000,000.

10,000,000 = 10^7

The number of prime numbers in the range 2 through 10^7 is approximately 10^7/ln(10^7) ≈ 620421

2.10.2: Euclid's Algorithm.

Consider an Euclid's algorithm with input integers y = 156 and x = 54.

1) What is the value of r at the beginning of the first iteration of the loop in Euclid's algorithm?

2) What is the value of r at the beginning of the second iteration of the loop in Euclid's algorithm?

3) What is the value of r after the second iteration of the loop in Euclid's algorithm?

4) How many times does the loop in Euclid's algorithm execute on input 156 and 54?

5) What is the gcd of 156 and 54?

1) 48

r = 156 mod 54 = 48

2) 6

x = 54, y = 48, r = 54 mod 48 = 6

3) 0

x = 48, y = 6, r = 48 mod 6 = 0

4) 2

After the second iteration of the loop, r = 0, so the loop executes two times.

5) 6

After the last iteration of the loop, y = 54, x = 6, and r = 0. Therefore the gcd is x = 6.

2.11.2: Extended Euclidean Algorithm

The image below shows the sequence of numbers generated by Euclid's algorithm on inputs 225 and 60 as well as partial results for the extended algorithm.

225 60 45 15

15 = 60 - (A * 45)

45 = 225 - (B * 60)

1) What is the correct value for the variable A?

2) What is the correct value for the variable B?

3) The two linear equations above can be used to express gcd(225, 60) as a linear combination of 225 and 60: 15 = C 225 + D 60. What is the correct value for C?

4) The two linear equations above can be used to express gcd(225, 60) as a linear combination of 225 and 60: 15 = C 225 + D 60 What is the correct value for D?

1) 1

A = 60 div 45 = 1

2) 3

B = 225 div 60 = 3

3) -1

15 = 60 - 45

45 = 225 - (3 · 60)

The second equation replaces 45 in the first equation with a linear combination of 225 and 60.

15 = 60 - (225 - 3 · 60) = 4·60 - 225

The coefficient of 225 is -1.

4) 4

15 = 60 - 45

45 = 225 - (3 · 60)

The second equation replaces 45 in the first equation with a linear combination of 225 and 60.

15 = 60 - (225 - 3·60) = 4·60 - 225.

The coefficient of 60 is 4.

Exercise 2.11.1: Applying the Euclidean Algorithm and the Extended Euclidean Algorithm

For each of the following pairs of numbers, find the gcd of the two numbers, and express the gcd as a linear combination of the two numbers.

a) 56 and 42

Exercise 2.11.1: Applying the Euclidean Algorithm and the Extended Euclidean Algorithm

For each of the following pairs of numbers, find the gcd of the two numbers, and express the gcd as a linear combination of the two numbers.

b) 81 and 60

2.12.2: Find the multiplicative inverse using the results of the Extended Euclidean Algorithm

1) Euclid's algorithm returns gcd(61, 54) = 1 = 26 · 54 - 23 · 61

What is the multiplicative inverse of 54 mod 61?

26

26 is the coefficient of 54 in the equation:1 = 26 · 54 - 23 · 61

The inverse of 54 mod 61 is (c mod 61), where c is the coefficient of 54:

26 mod 61 = 26

2.12.2: Find the multiplicative inverse using the results of the Extended Euclidean Algorithm

2) Euclid's algorithm returns gcd(14, 33) = 1 = 3 · 33 - 7 · 14.

What is the multiplicative inverse of 14 in Z33? (the 33 is subscript)

26

-7 is the coefficient of 14 in the equation:1 = 3 · 33 - 7 · 14

The inverse of 14 in Z33 is (c mod 33), where c is the coefficient of 14:

-7 mod 33 = 26

Exercise 2.12.1: Computing a multiplicative inverse

For each x and n, find the multiplicative inverse mod n of x. Your answer should be an integer s in the range 0 through n - 1. Check your solution by verifying that sx mod n = 1.

a) x = 52, n = 77

Exercise 2.12.1: Computing a multiplicative inverse

For each x and n, find the multiplicative inverse mod n of x. Your answer should be an integer s in the range 0 through n - 1. Check your solution by verifying that sx mod n = 1.

b) x = 77, n = 52

From the solution to the previous problem:

gcd(77, 52) = 1 = 25·77 - 37·52

The coefficient of 77 in the equation above is 25. The multiplicative inverse of 77 mod 52 is (25 mod 52) = 25.

Check: 77·25 mod 52 = 1925 mod 52 = 1

Exercise 2.12.1: Computing a multiplicative inverse

For each x and n, find the multiplicative inverse mod n of x. Your answer should be an integer s in the range 0 through n - 1. Check your solution by verifying that sx mod n = 1.

c) x = 53, n = 71

Exercise 2.14.1: Converting from non-decimal bases to decimal.

Compute the decimal representation for each of the following numbers.

a) (1100110)2 (2 is subtext)

2^6 + 2^5 + 2^2 + 2^1 = 64 + 32 + 4 + 2 = 102

Exercise 2.14.1: Converting from non-decimal bases to decimal.

Compute the decimal representation for each of the following numbers.

b) (346)7 (7 is subtext)

3·7^2 + 4·7^1 + 6·7^0 = 3·49 + 4·7 + 6 = 181

Exercise 2.14.1: Converting from non-decimal bases to decimal.

Compute the decimal representation for each of the following numbers.

c) (120121)3 (3 is subtext)

1·3^5 + 2·3^4 + 1·3^2 + 2·3^1 + 1·3^0 = 243 + 2·81 + 9 + 2·3 + 1 = 421

Exercise 2.14.1: Converting from non-decimal bases to decimal.

Compute the decimal representation for each of the following numbers.

d) (50020)8 (8 is subtext)

5·8^4 + 2·8^1 = 5·4096 + 2·8 = 20496

2.15.1: Hexadecimal expansions

1) What is the decimal expansion of (2F)16? (16 is subtext)

47

2 is in the 16's place and F (which corresponds to 15) is in the 1's place. Therefore, (2F)16 = 2 · 16^1 + 15 · 16^0= 47

2.15.1: Hexadecimal expansions

2) What is the binary expansion of (2F)16? Omit the leading zeroes in your answer. (16 is subtext)

101111

0010 corresponds to 2 and 1111 corresponds to F. Put 0010 and 1111 together to get 00101111 and drop the leading zeroes to get 101111.

2.15.1: Hexadecimal expansions

3) What is the hexadecimal number that corresponds to 1011101?

5D

The rightmost four bits, 1101, corresponds to D. The remaining bits on the left are 101. Add a leading zero to 101 on the left to get 0101 which corresponds to 5. Therefore 1011101 corresponds to a hexadecimal expansion of 5D.

Exercise 2.15.1: Converting from hex to binary.

Give a binary representation for each number given below in hex. Drop the leading zeroes in your binary representation.

a) (A3)16 (16 is subtext)

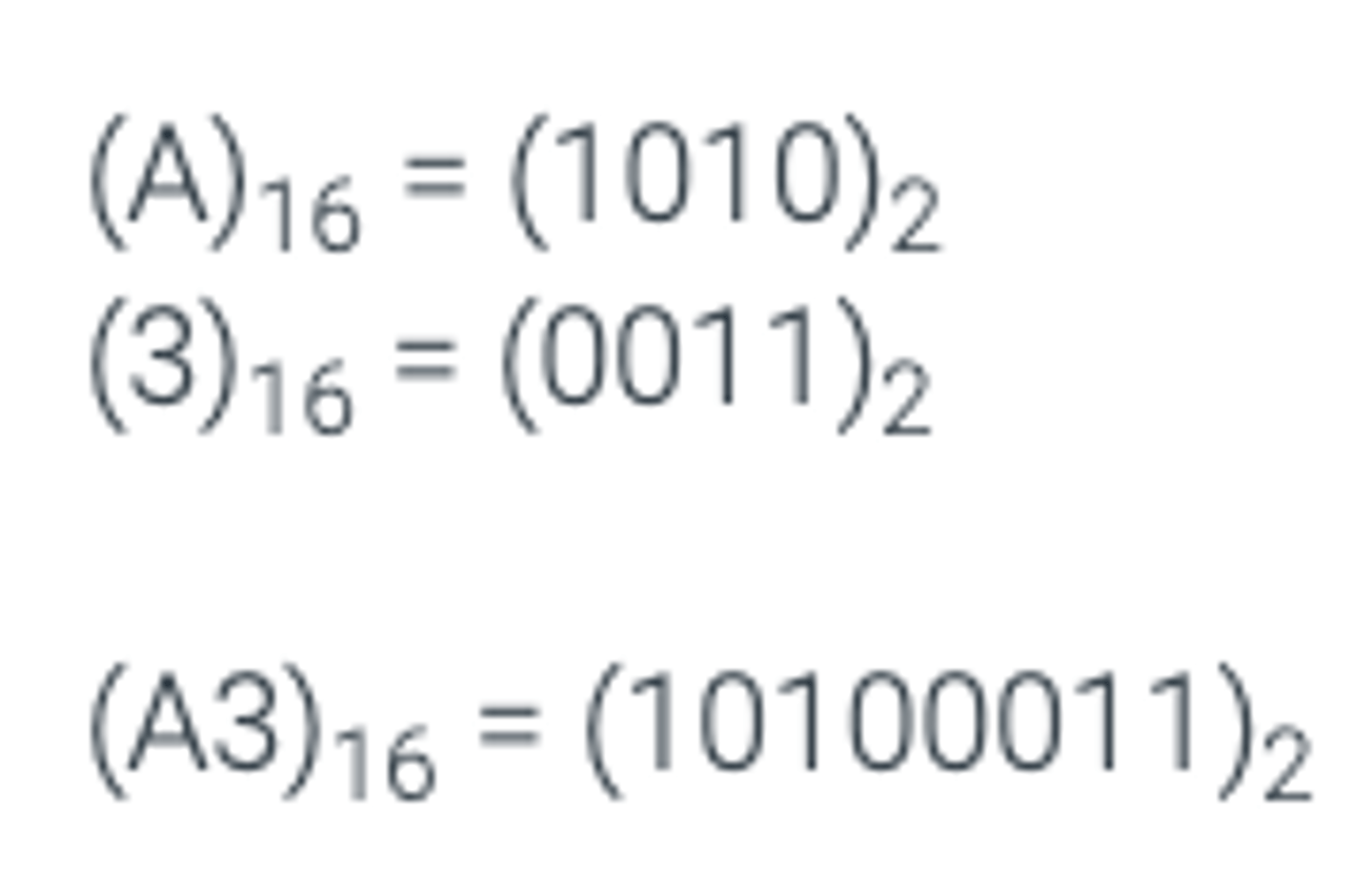
Exercise 2.15.1: Converting from hex to binary.

Give a binary representation for each number given below in hex. Drop the leading zeroes in your binary representation.

b) (1FC)16 (16 is subtext)

Exercise 2.15.1: Converting from hex to binary.

Give a binary representation for each number given below in hex. Drop the leading zeroes in your binary representation.

c) (2A0B)16 (16 is subtext)

Exercise 2.15.2: Converting from binary to hex.

Give a hexadecimal representation for each number given below in binary.

a) 101

Exercise 2.15.2: Converting from binary to hex.

Give a hexadecimal representation for each number given below in binary.

b) 11101

Exercise 2.15.2: Converting from binary to hex.

Give a hexadecimal representation for each number given below in binary.

c) 101101101000010101

2.16.2: Conversion to expansion base b

1) Find the expansion base 5 of 57.

212

57 mod 5 = 2; Rightmost digit is 2.

57 div 5 = 11

11 mod 5 = 1; Next digit to the left is 1.

11 div 5 = 2

2 mod 5 = 2; Next digit to the left is 2.

2 div 5 = 0

2.16.2: Conversion to expansion base b

2) Find the expansion base 7 of 52.

103

52 mod 7 = 3; Rightmost digit is 3.

52 div 7 = 7

7 mod 7 = 0; Next digit to the left is 0.

7 div 7 = 1

1 mod 7 = 1; Next digit to the left is 1.

1 div 7 = 0

2.16.2: Conversion to expansion base b

3) Find the binary of 21.

10101

21 mod 2 = 1; Rightmost bit is 1.

21 div 2 = 10

10 mod 2 = 0; Next bit to the left is 0.

10 div 2 = 5

5 mod 2 = 1; Next bit to the left is 1.

5 div 2 = 2

2 mod 2 = 0; Next bit to the left is 0.

2 div 2 = 1

1 mod 2 = 1; Next bit to the left is 1.

1 div 2 = 0

2.16.3: Number of digits base b

In the questions below, assume that numbers are expressed without any leading zeroes.

1) How many digits are required to express the base 7 expansion of 2401?

⌈log7⁡ 2402⌉

⌈log7⁡ 2401⌉

(7 is subtext)

2.16.3: Number of digits base b

In the questions below, assume that numbers are expressed without any leading zeroes.

2) How many digits are required to express the base 8 expansion of 9?

⌈log9⁡ 9⌉

⌈log8⁡ 10⌉

(the 9 and 8 after log are subtext)

2.16.3: Number of digits base b

In the questions below, assume that numbers are expressed without any leading zeroes.

3) How many digits are required to express the binary expansion of 2^55?

56

55

The binary expansion of 2^55 is a 1 followed by 55 0's.

2.16.3: Number of digits base b

In the questions below, assume that numbers are expressed without any leading zeroes.

4) How many digits are required to express the base 8 expansion of 87 - 1?

7

8

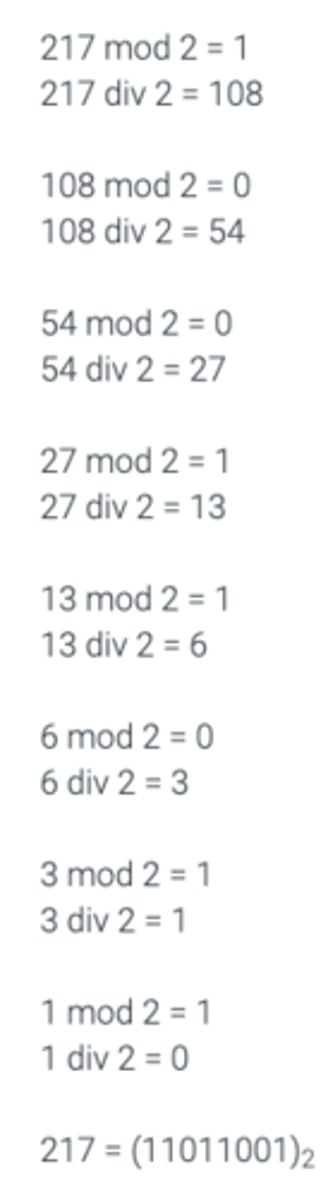
Exercise 2.16.1: Converting from decimal to non-decimal bases.

A number N is given below in decimal format. Compute the representation of N in the indicated base.

a) N = 217, binary

Exercise 2.16.1: Converting from decimal to non-decimal bases.

A number N is given below in decimal format. Compute the representation of N in the indicated base.

b) N = 344, hex

Exercise 2.16.1: Converting from decimal to non-decimal bases.

A number N is given below in decimal format. Compute the representation of N in the indicated base.

c) N =136, base 7

2.18.2: Expressing exponents as products of terms whose exponents are powers of 2

1) 7 = 22 + 21 + 20

Which expression is equivalent to 57?

5^2^2⋅5^2^0

5^2^2⋅5^2^1⋅5^2^0

5^2^3⋅5^2^2⋅5^2^0

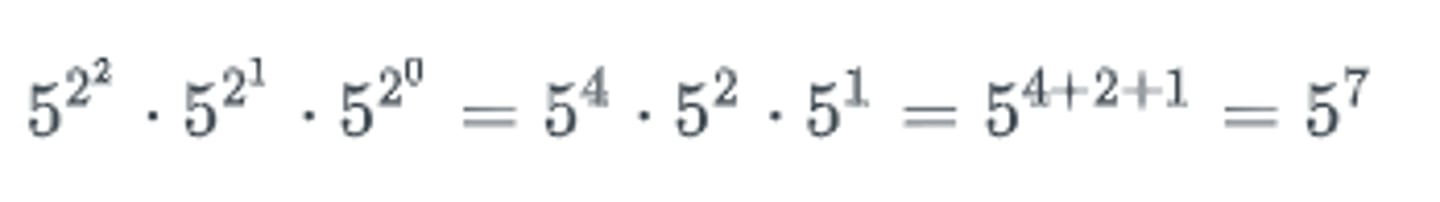
2.18.2: Expressing exponents as products of terms whose exponents are powers of 2

2) The binary representation of 25 is 11001. Which expression is equivalent to b^25?

b^2^5⋅b^2^4⋅b^2^1

b^2^2⋅b^2^1

b^2^4⋅b^2^3⋅b^2^0

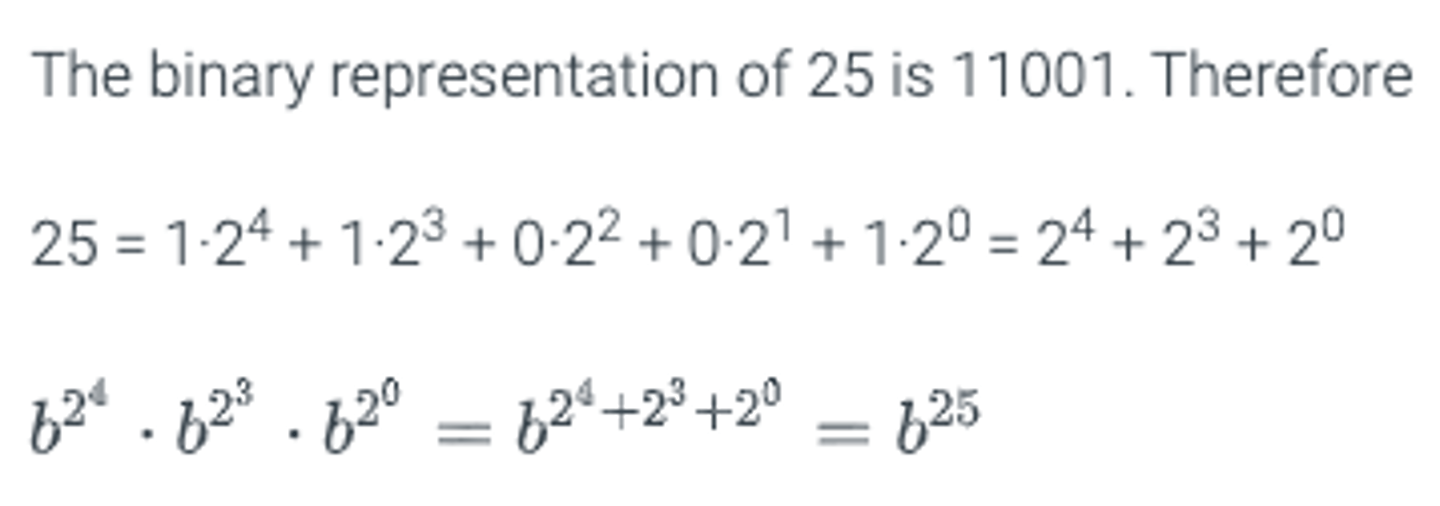
2.18.2: Expressing exponents as products of terms whose exponents are powers of 2

3) The binary representation of 18 is 10010. Which expression is equivalent to b^18?

b^2^5⋅b^2^2

b^2^4⋅b^2^1

b^2^3⋅b^2^0

Exercise 2.18.1: Expressing exponents as a product of terms whose exponents are powers of 2

For each value of y, express by as a product of terms of the form b^2^j, where j is a non-negative integer.

a) y = 53