Arithmetic and Geometric Sequences

The arithmetic sequence is numbers moving with _____ or _____.

Addition or subtraction

The geometric sequence is numbers moving with _____ or _____.

Multiplication or division

What is the pattern in this set of numbers and which type of sequence is it?

8, 4, 0, -4, …

It is being subtracted by 4, so the pattern is -4

It is being subtracted so it is arithmetic

What is the pattern in this set of numbers and which type of sequence is it?

3, -9, 27, -81

It is geometric because it is being multiplied by -3. Check calc for understanding.

What is a sequence?

A list of numbers.

a_n is the same as…

f(n)

f_n is the same as…

a_n

What does the n in a_n represent?

The term number you are looking for. Most likely it will be a₁ since that what most problems start with.

For example if you was looking for the 50th term, that would be a₅₀ = ….

What does the a represent in a_n ?

It is a placeholder for that number term. For example, lets say you have the sequence: 2,6,10,14,18. If you had a₁ then it would be equal to 2, then a₂ = 6, and so forth.

What is a₃ in this sequence?

2,6,10,14,18

a₃ = 10

How would you find the previous term?

a_{n - 1}

a_{n - 1} is how you find…

the previous term in a sequence.

How would you find the next term in a sequence?

a_{n + 1}

a_{n + 1} is how you find…

the next term in a sequence

a_n would represent the ___ term in a sequence

current

If you can not find the r in a geometric sequences, you have to ____ for r.

solve

r represents the…

common ratio

The common ratio is represented by…

r

n = ?

the term number

a₁ is the ___ term.

first

a₄ is the ___ term.

fourth

a₃ is the ___ term.

third

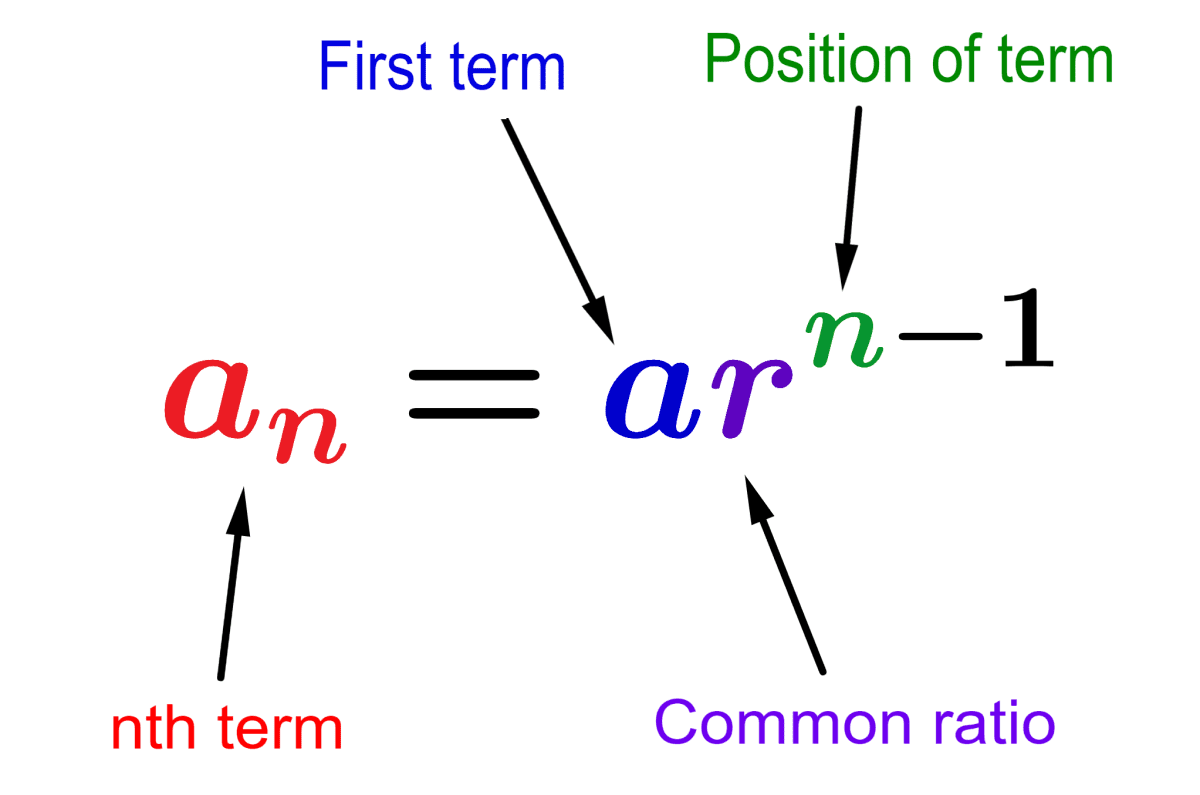
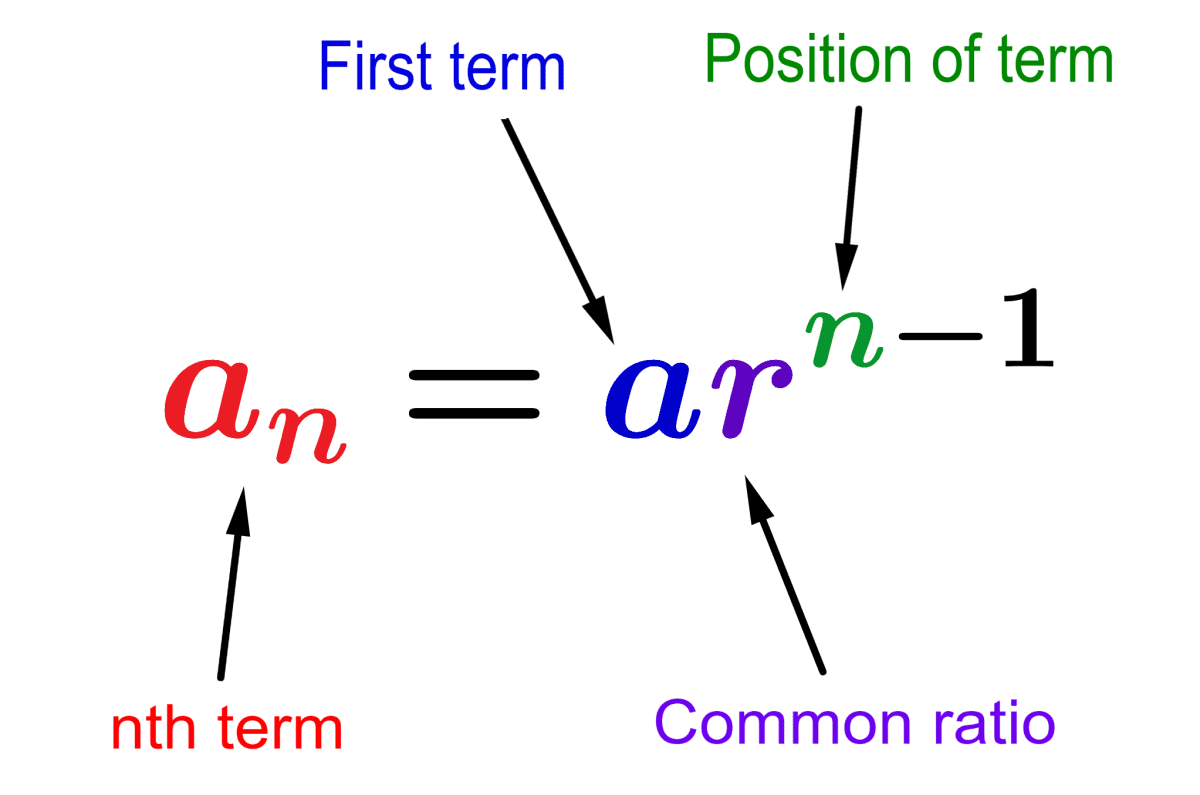
What is the formula for finding a geometric term ( finding a term in the geometric sequence?)

a_n= a₁ (r)^{n - 1}

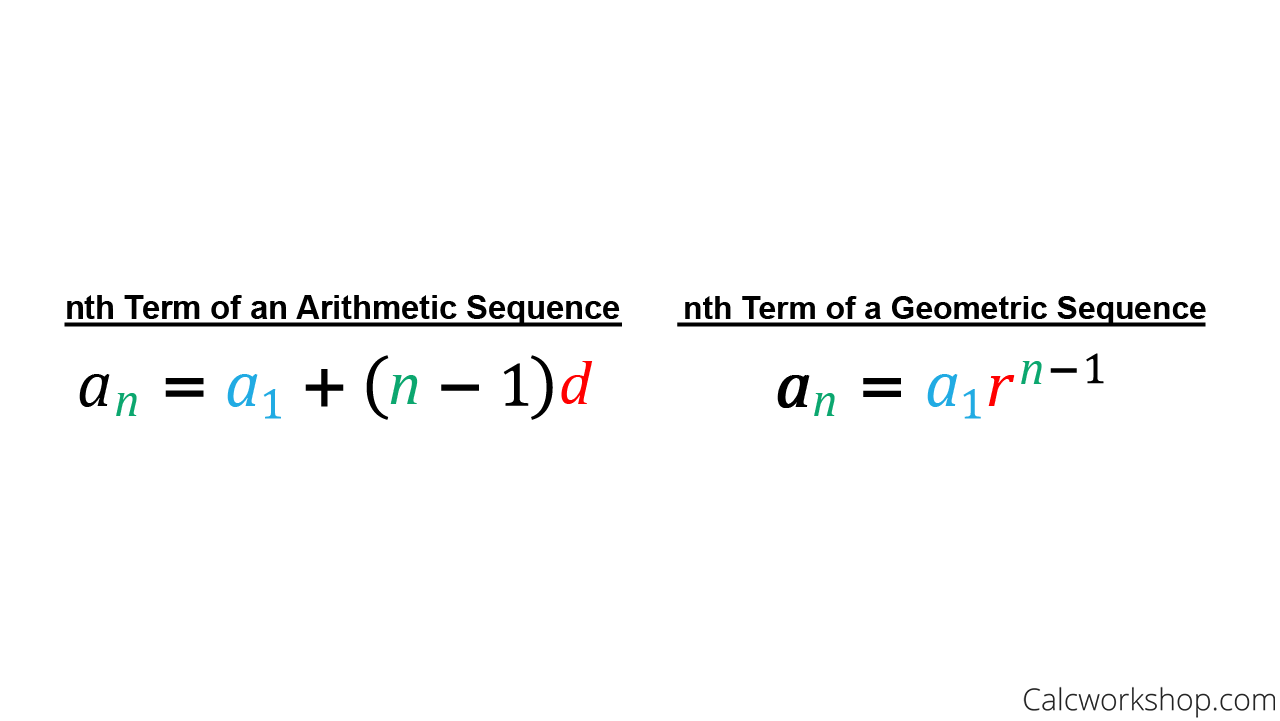
If you need to find the third or fourth term in a geometric system, but you only have the first term, what do you do?

Use the geometric sequence formula:

a_n= a₁ (r)^{n - 1}

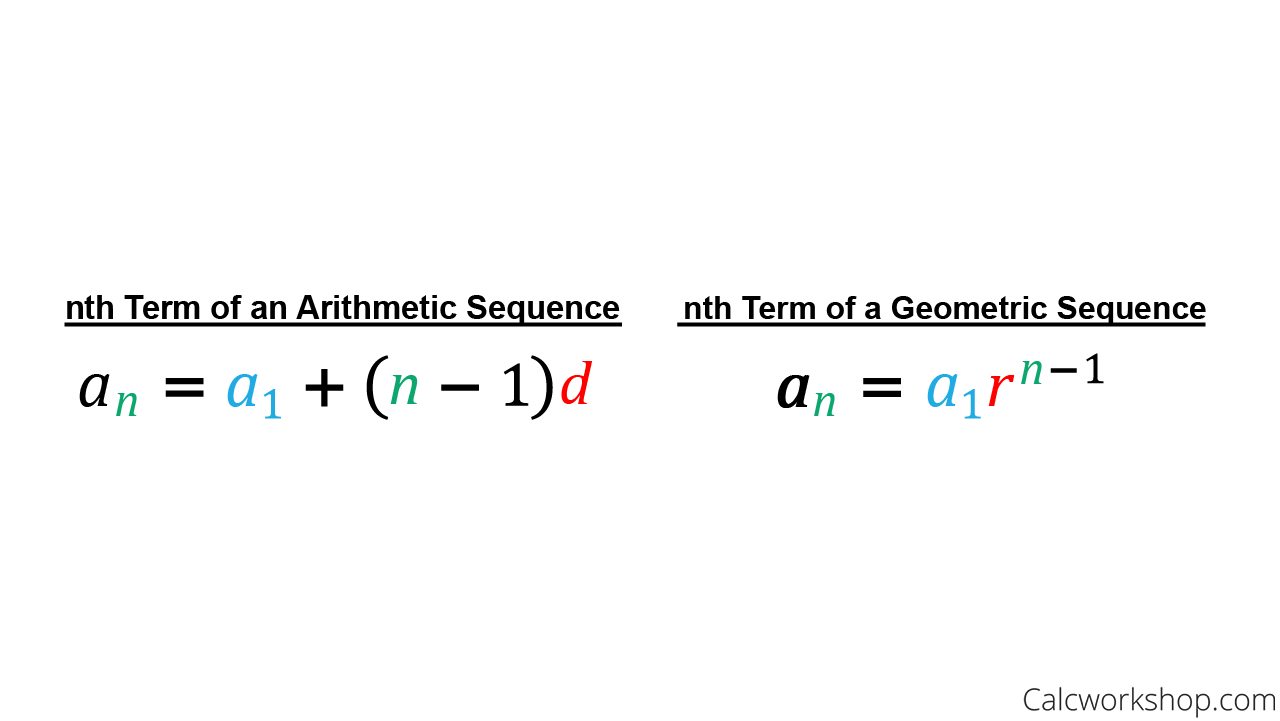
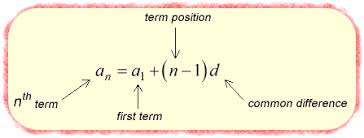
What is the formula for finding a arithmetic term ( finding a term in the arithmetic sequence?)

a_n = a₁ + (n - 1)d

If you need to find the n^th term (any term) of an arithmetic sequence, what do you do?

Use the arithmetic formula:

a_n = a₁ + (n - 1)d

What does d represent in the arithmetic formula?

d represents the common difference between consecutive terms in the arithmetic sequence. but practically its the; 2nd term - 1st term.

What is a common formula for finding d ?

d = a_n - a_n-1

a₂ - a₁ would be a possible formula for finding…

the common difference “d” in an arithmetic sequence.

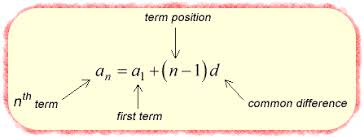
Find the 50th term of the sequence:

3,5,7,9,11,…

a₁ = 3. n = 50. 5-3 = 2 = d

a₅₀ = 3 + (50 - 1)2. Input into calc.

a₅₀ = 100

Find the first four terms of the recursive formula (n - 1) below:

a₁ = 5.

a_n = 3 + 2a_{n - 1}

a₁ = 5, a₂ = 13, a₃ = 29, a₄ = 61

What does r represent in the geometric sequence?

The common ratio, what you’re multiplying or dividing by

How do you find the common ratio, or r of a geometric sequence?

To find the common ratio r of a geometric sequence, divide any term by its preceding term (a_n / a_n-1), which remains constant throughout the sequence. Most likely it’ll by a₂ / a₁

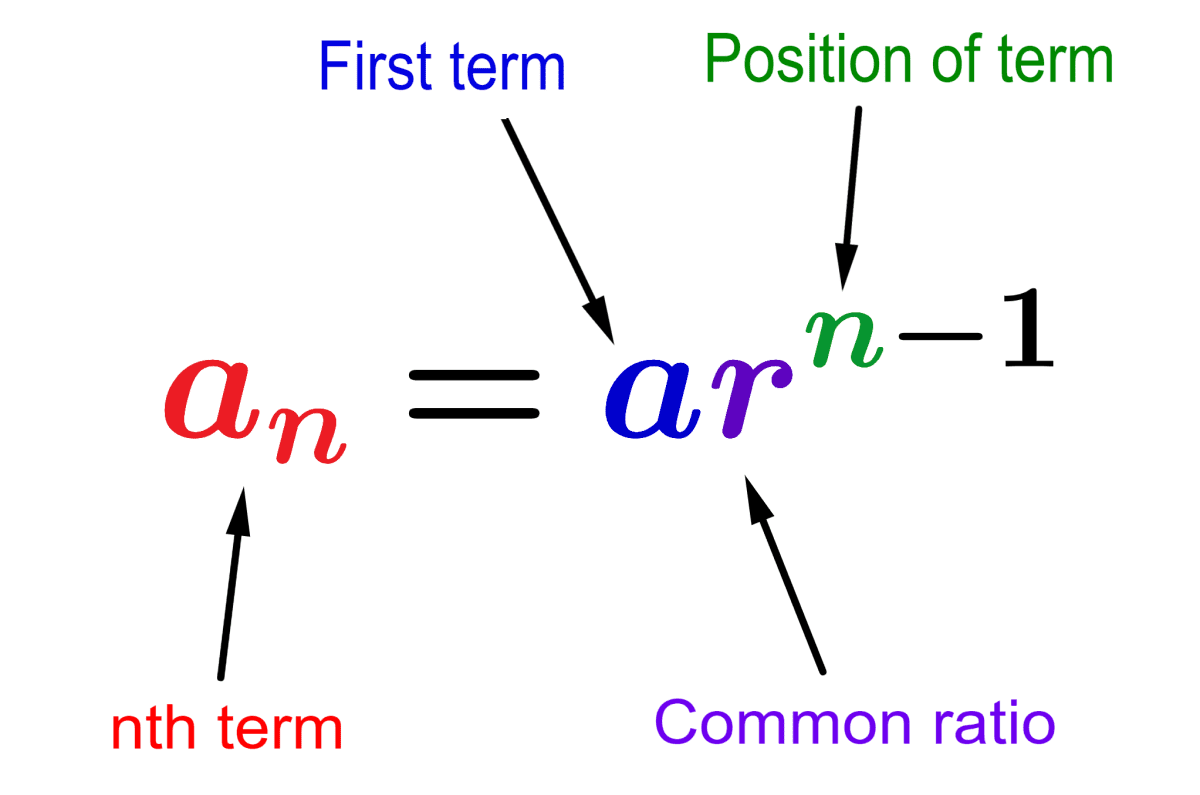
Find the 7^th term of the sequence:

2,6,18,54

r = 6/2 = 3

a₇ = 2(3)^{7 - 1}

= 2(3)⁶ = 1458

a₇ = 1458

What is the common difference of the arithmetic sequence 5,8,11,14?

d = a_n - a_{n - 1} or a₂ - a₁. 8 - 5 = 3

d = 3

The common difference is represent by…

d

How would you find the previous term or next term if you only have one term and d?

a_n = a_n-1 + d or for example if you wanted to find a₃ you would use a₃ = a₂ + d

In arithmetic sequence, each term is found by adding the ____ _____ to the previous term.

common difference. Which can be represented by: a_{n + 1} = a_n + d

In an arithmetic sequence, the first term is 4 and the third term is -2. What is the common difference.

The common difference can be calculated by subtracting the first term from the third term and then dividing by the number of terms between them. In this case, the common difference is -2 - 4, divided by 2, which equals -3.

The common difference is calculated as (-2 - 4) / 2 = -3.

When finding the common difference between terms that are far apart (ex: a₁ and a₄), what do you do?

Divide d by the number of terms between them.

remember d = a_n - a_{n - 1}. But in this case they are far apart, so you have to divide by the amount of steps between them. So in this case, you would divide a₄ - a₁ by 3, or d/3.

Which one has a geometric sequence with a common ratio of -3?

1) -10, -7, -4,1,…

2) 14,11,8,5,…

3) -2,-6,-18,-54,…

4) 4,-12,36,-108,…

r = a₂ / a₁. -12/4 = -3, thus the answer is 4.

Determine the common difference of the arithmetic sequence in which

a₁ = 3 and a₄ = 15.

The common difference can be found by subtracting the first term from the fourth term and dividing by the number of intervals between them. Here, the common difference is (15 - 3) / 3 = 4.

Or just use basic addition. 3 + 4 + 4 + 4 = 15.

What is the common ratio of this geometric sequence?

1/2, 2, 8, 32, ….

r = a₂ / a₁. 2/ (1/2) = 4.

r = 4

What is the common ratio of the geometric sequence whose first term is 27 and fourth term is 64?

r = 4/3

What is the common ratio of the geometric sequence whose first term is 5 and third term is 245?

r = 7

Just use process of elimination here

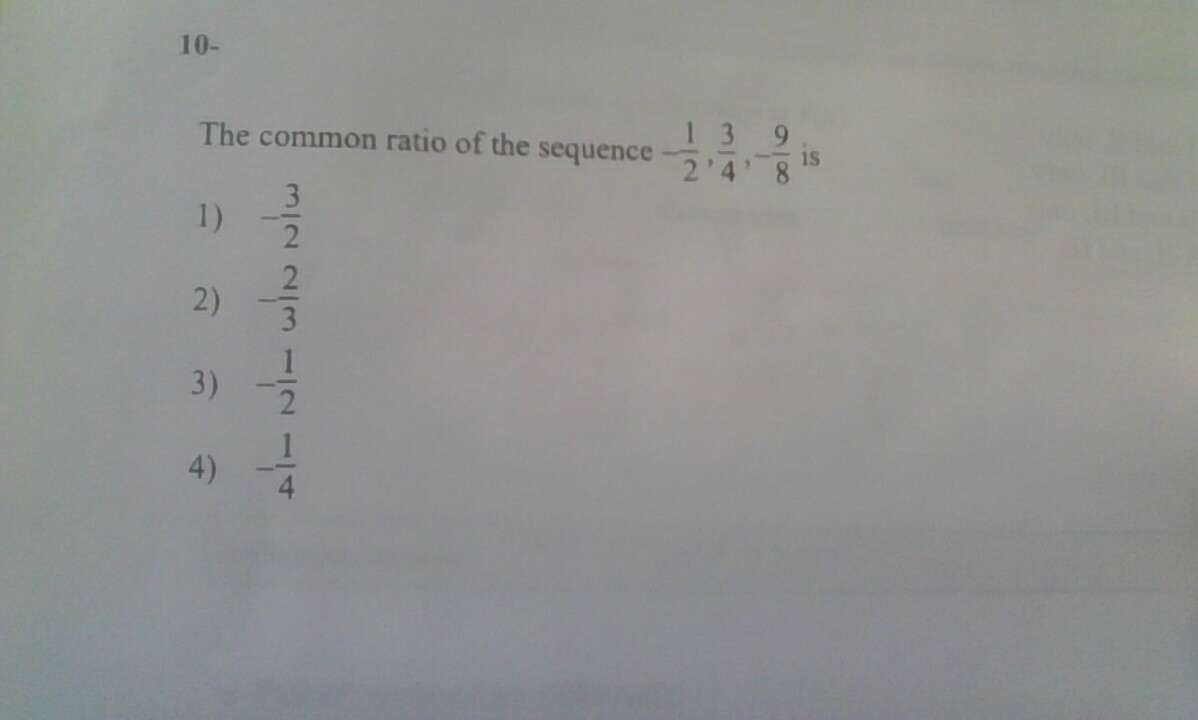
Pick options one through four.

Remember r = a₂ / a₁. Dividing fractions can be a bit tricky, so its best to use a calculator for this.

3/2 / (-1/2) = -3/2. This means r = -3/2

Remeber, when trying to find the ratio between the first two terms, the rule: _______ can be applied

r = a₂/a₁

Given the following three sequences:

1): 2,4,6,8,10….

2): 2,4,8,16,32….

3): a, a + 2, a + 4, a + 6, a + 8….

Which ones are arithmetic sequences?

1 and 3, only.

Find the 7th term of this sequence:

2,3, 9/2,…

The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary).

a₇ = 22.781

Note: when using calculator if get a fraction and you want it in decimal form use the / button instead of the actual fraction.

Find the 9th term of this sequence:

3,6,12…

The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary).

a₉ = 768

Find the 46th term of this sequence:

9,16,23,...

The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary).

a₄₆ = 324

Find the 7th term of this sequence:

5,30,180…

The first three terms of a sequence are given. Write your answer as a decimal or whole number. Round to the nearest thousandth (if necessary).

a₇ = 233280

The geometric series is used to find the _____ of all the numbers in a sequence

sum/total

What does the S represent in the geometric series?

The sum.

What is the geometric series formula?

S_n = a₁ - a₁rⁿ / 1 - r

where Sn is the sum of the first n terms, a1 is the first term, r is the common ratio, and n is the number of terms.

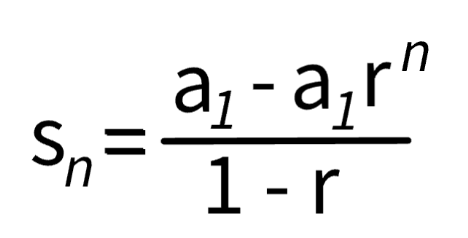
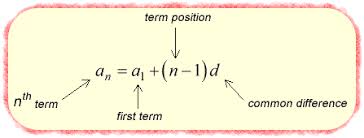
Find the 60th term of the arithmetic sequence:

-27,-24, -21,…

a₆₀ = 150

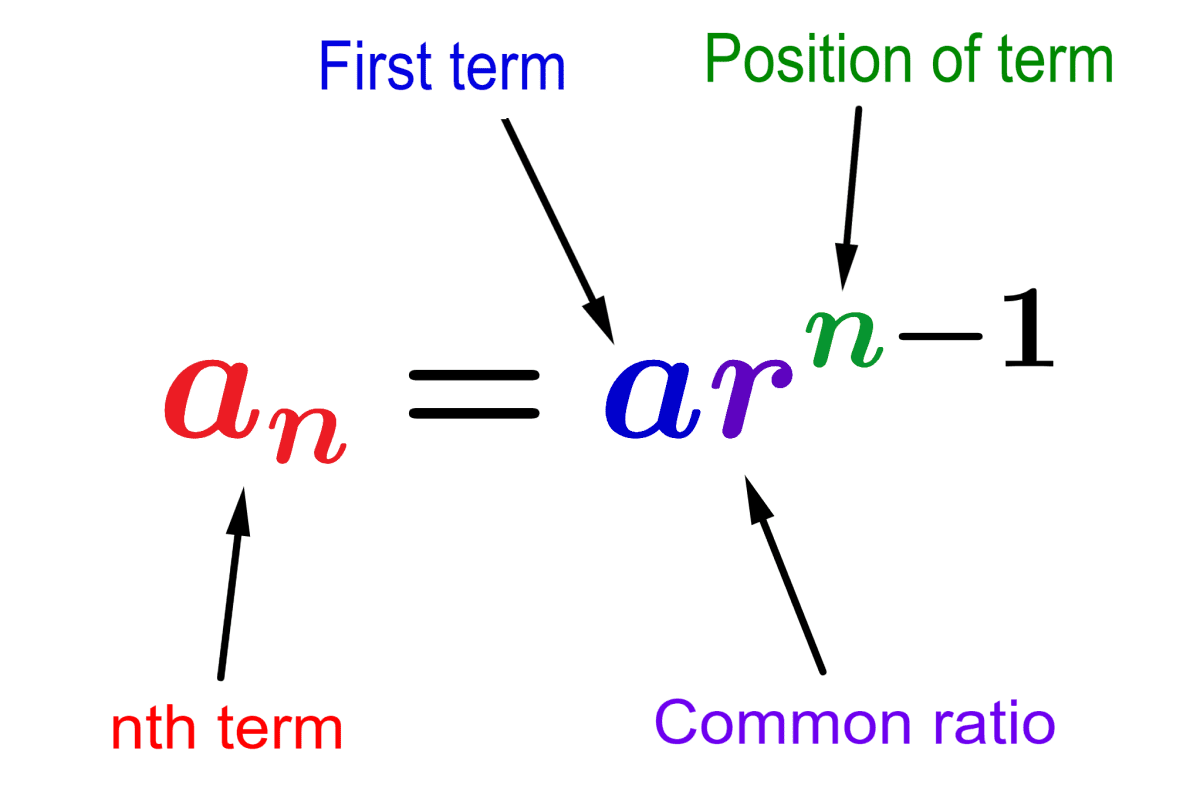
Find the 11th term of the geometric sequence:

1,3,9…

a₁₁ = 59049

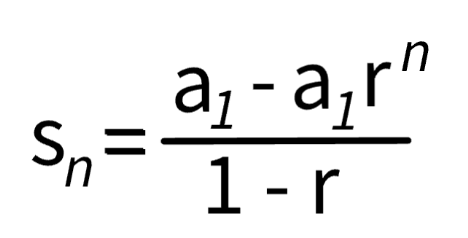
Find the sum of the first 9 terms of the following sequence:

3, -15, 7,…

Round to the nearest hundredth if necessary.

1. Identify the type of sequence: Determine if the sequence is arithmetic or geometric by checking for a common difference or a common ratio.

* Check for common difference: -15 - 3 = -18, 75 - (-15) = 90 (Not arithmetic)

* Check for common ratio: -15 / 3 = -5, 75 / -15 = -5 (Geometric)

2. Identify the first term (a₁): The first term is 3.

3. Identify the common ratio (r): The common ratio is -5.

4. Identify the number of terms (n): We want the sum of the first 9 terms, so n = 9.

5. Use the formula for the sum of the first n terms of a geometric sequence:

6. Substitute the values into the formula: S₉ = 3 * (1 - (-5)⁹) / (1 - (-5)).

7. Calculate the result following the order of operations:

* Calculate the exponent: (-5)⁹ = -1953125.

* Calculate the numerator: 1 - (-1953125) = 1 + 1953125 = 1953126.

* Calculate the denominator: 1 - (-5) = 1 + 5 = 6.

Substitute back into the formula: S₉ = 3 (1953126) / 6.

* Perform the multiplication and division: S₉ = 5859378 / 6 = 976563.

Result: The sum of the first 9 terms is 976563.

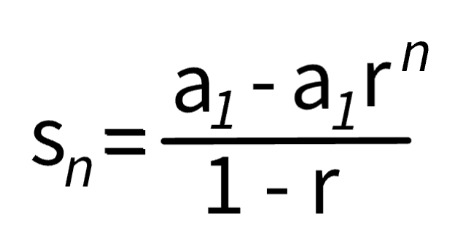
Find the sum of the first 10 terms of the following series, to the nearest integer.

8, 20/3, 50/9,…

Summary of Steps:

1. Identify the type of series: Determine if the series is arithmetic or geometric by checking for a common difference or a common ratio.

2. Identify the first term (a₁): The first term is 8.

3. Identify the common ratio (r): The common ratio is 5/6.

4. Identify the number of terms (n): We want the sum of the first 10 terms, so n = 10.

5. Use the formula for the sum of the first n terms of a geometric series: S_n = a₁ * (1 - r^n) / (1 - r).

6. Substitute the values into the formula: S₁₀ = 8 * (1 - (5/6)¹⁰) / (1 - 5/6).

7. Calculate the components of the formula

8. Substitute the calculated components back into the formula for S₁₀: S₁₀ = 8 * (50,700,551 / 60,466,176) / (1/6).

9. Simplify and calculate the result:

10. Round to the nearest integer: Round 40.2478... to the nearest integer, which is 40.

Result: The sum of the first 10 terms, rounded to the nearest integer, is 40.

When doing the recursive formula, always put _ as the ____ term.

n as the next term. so if you have a₁, start with a₂

If a₁ = 5 and a_n = a_{n - 1} - 4 then find the value of a₆.

Remember a_n always represent a number, so you have to replace it with that number to continue.

Starting with a₁ = 5, apply the recursive formula to find subsequent terms:

a₂ = 5 - 4 = 1, a₃ = 1 - 4 = -3, a₄ = -3 - 4 = -7, a₅ = -7 - 4 = -11, a₆ = -11 - 4 = -15. Thus, a₆ = -15.

If a₁ = 8 and a_n = -3a_{n - 1} then find the value of a₄.

Starting with a₁ = 8, apply the recursive formula:

a₂ = -3(8) = -24, a₃ = -3(-24) = 72, a₄ = -3(72) = -216. Thus, a₄ = -216.

If a₁ = 9 and a_n =-3a_{n - 1} - 5 then find the value of a₅.

Starting with a₁ = 9, apply the recursive formula:

a₂ = -3(9) - 5 = -32, a₃ = -3(-32) - 5 = 91, a₄ = -3(91) - 5 = -278, a₅ = -3(-278) - 5 = 829. Thus, a₅ = 829.

If a₁ = 2 and a_n = (a_{n - 1})² + 5 the find the value of a₄.

Starting with a1 = 2, apply the recursive formula: a2 = (2)² + 5 = 9, a3 = (9)² + 5 = 86, a4 = (86)² + 5 = 7401. Thus, a4 = 7401.

If a₁ = 1 and a_n = -5(a_n-1) + 2 then find the value of a₃.

Starting with a₁ = 1, apply the recursive formula: a₂ = -5(1) + 2 = -3, a₃ = -5(-3) + 2 = 17. Thus, a₃ = 17.

Find the 9th term in this arithmetic sequence:

4x - 4, -x - 1, -6x + 2,…

a₉ = -36x + 20