Quantum Mechanics term 1

What is Compton Scattering?

The scattering of high-energy photons on free electrons, where the photon loses energy (wavelength increases) and the electron gains kinetic energy. This effect provides further evidence for the particle-like nature of light.

What is the equation for the change in wavelength after Compton scattering?

λ′−λ=2πℏ​(1−cosθ)/Mc

where λ′ and λ are photon wavelengths after and before scattering, M is electron mass, and θ is the scattering angle.

What is the equation for the energy levels of a hydrogen atom according to the Bohr model?

E_{n}=-\frac{2\pi\hbar cR_0}{n^2}

​ where R₀​ is the Rydberg constant and n is an integer.

What is the Time-Dependent Schrödinger Equation (1D)?

i\hbar\partial\psi(x,t)/\partial t=-\frac{\hbar^2}{2M}\frac{\partial^2\psi(x,t)}{\partial x^2}+V(x,t)\psi(x,t)

where M is particle mass, V(x,t) is potential, and ψ(x,t) is the wave function.

What is the Wave Function (ψ(x,t))?

A mathematical function that describes the quantum state of a particle or system. It can be complex and its magnitude squared gives the probability of finding the particle at a given location.

What is the Born Postulate?

The postulate that the probability of finding a particle in a given interval is proportional to the square of the magnitude of its wave function:

P(x,t)dx=\vert\psi(x,t)\vert^2dx

What are the general boundary conditions for a valid wave function?

It must be continuous, single-valued, and normalizable (integral of squared modulus is finite). Its first derivative must be continuous, except where the potential is infinite.

What is the Time-Independent Schrödinger Equation?

-\frac{\hbar^2}{2M}\frac{d^2\phi\left(x\right)}{\differentialD x^2}\left.+V(x\right)\phi(x)=E\phi(x), used for systems where the potential V(x) does not change with time.

What is a Particle in an Infinite Square Well, and what is its key quantum mechanical phenomenon?

A particle confined to a region of zero potential, with infinite potential walls. The key phenomenon is energy quantization, meaning the particle can only exist at specific, discrete energy levels.

What is the equation for the quantized energy levels of a particle in an infinite square well of width 2a?

En=\frac{\hbar^2\pi^2}{8Ma^2}n^2

where n is a positive integer (quantum number).

What is Quantum Tunneling?

A quantum mechanical phenomenon where a particle can pass through a potential barrier, even if its energy is less than the barrier height. Classically, this would be impossible.

What is the potential for a One-Dimensional Harmonic Oscillator?

V(x)=kx^2/2

where k is the effective spring constant.

How are dynamical variables represented in Quantum Mechanics?

Dynamical variables (like position, momentum, energy) are represented by operators.

What is the Momentum Operator in 3D?

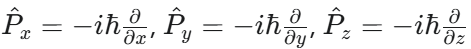
If a system is in a superposition of states, how do you determine the probability of measuring a specific eigenvalue?

If the wave function is \psi=∑_{n}a_{n}\phi_{n} ,the probability of obtaining the eigenvalue corresponding to ϕ_n​ is

\left\vert a_{n}\right\vert^2

What is the significance of the commutation relation between two operators?

If two operators A^ and B^ commute ([A^,B^]=0), then measuring the corresponding dynamical variables in succession yields results independent of the measurement order. If they do not commute, the order of measurement matters.

What are the eigenvalues of the angular momentum operator

The eigenvalues are ℏm, where m is an integer

What are the eigenvalues of the squared angular momentum operator?

\lambda=\hbar^2l\left(l+1\right)

where l is a non-negative integer (l=0,1,2,...).

What are the eigenfunctions for angular momentum (simultaneous eigenfunctions of L^(^2) and L^_z​)?

Spherical Harmonics, denoted as Y_{lm}\left(\theta,\varphi\right)

What is the equation for the quantized energy levels of a particle in a 3D infinite potential well (box with dimensions a,b,c)?

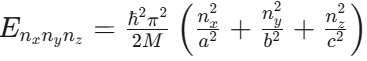
What is Degeneracy in the context of quantum energy levels?

When multiple distinct quantum states (different combinations of quantum numbers) have the same energy.

What is the equation for the energy levels of a 3D Harmonic Oscillator?

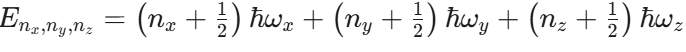
What is the equation for the energy levels of hydrogen-like atoms?

where Z is the atomic number

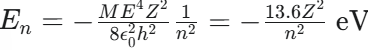
What does the Stern-Gerlach experiment demonstrate?

It demonstrates space quantization and the existence of spin angular momentum, an intrinsic angular momentum of particles not associated with orbital motion

What are the Pauli Spin Matrices (for spin-1/2 particles)?

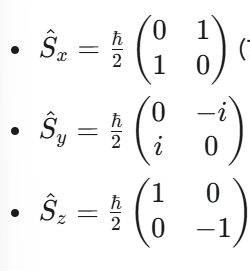
What is the Pauli Exclusion Principle?

The principle that states each quantum state (defined by the quantum numbers n,l,m_l​,m_s​) can hold only one electron. This principle is crucial for explaining the periodic table.

What is Spin-Orbit Coupling?

The interaction between an electron's spin angular momentum and its orbital angular momentum, leading to fine structure in atomic spectra.

What is the Weak-Field Zeeman Effect?

The splitting of atomic energy levels when an atom is placed in a weak external magnetic field.

What are Selection Rules in photon emission from atoms?

Rules that govern which transitions between energy levels are allowed or forbidden, based on changes in quantum numbers. For example, electric dipole transitions typically allow changes in the orbital quantum number by Δl=±1.