Math - TEAS, TEAS- Math

Order of Operations (PEMDAS)

Parenthesis

Exponents

Multiplication

Division

Addition

Subtraction

Whole Numbers

1,2,3,4, etc..

Steps for Solving Word Problems

1. Read Problem Carefully

2. Determine whats being asked

3. Underline the Important information

4. Set up Problem

5. Solve Problem

6. Check Answer

Mixed Numbers

Number that represents the sum of a whole number and a proper fraction

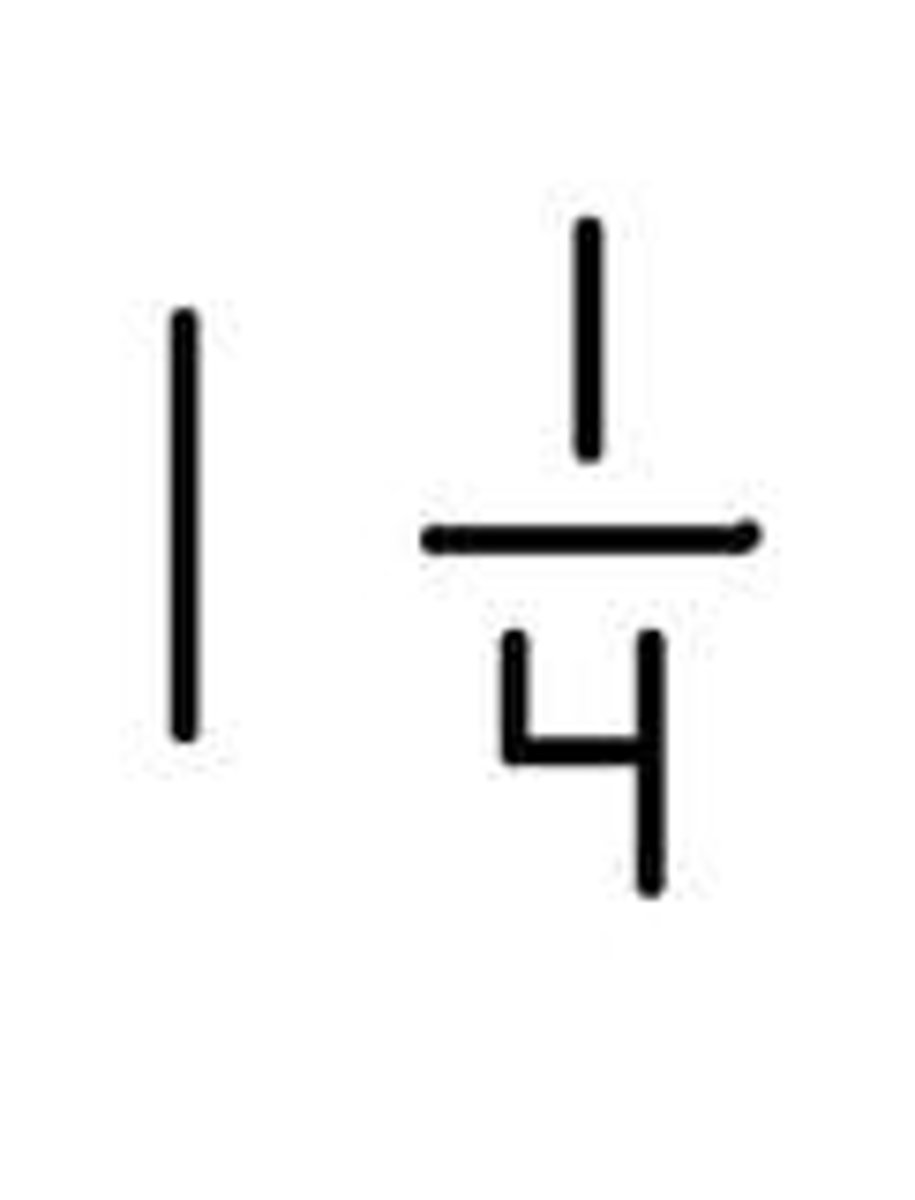
Improper Fraction

fraction whose numerator is larger than its denominator

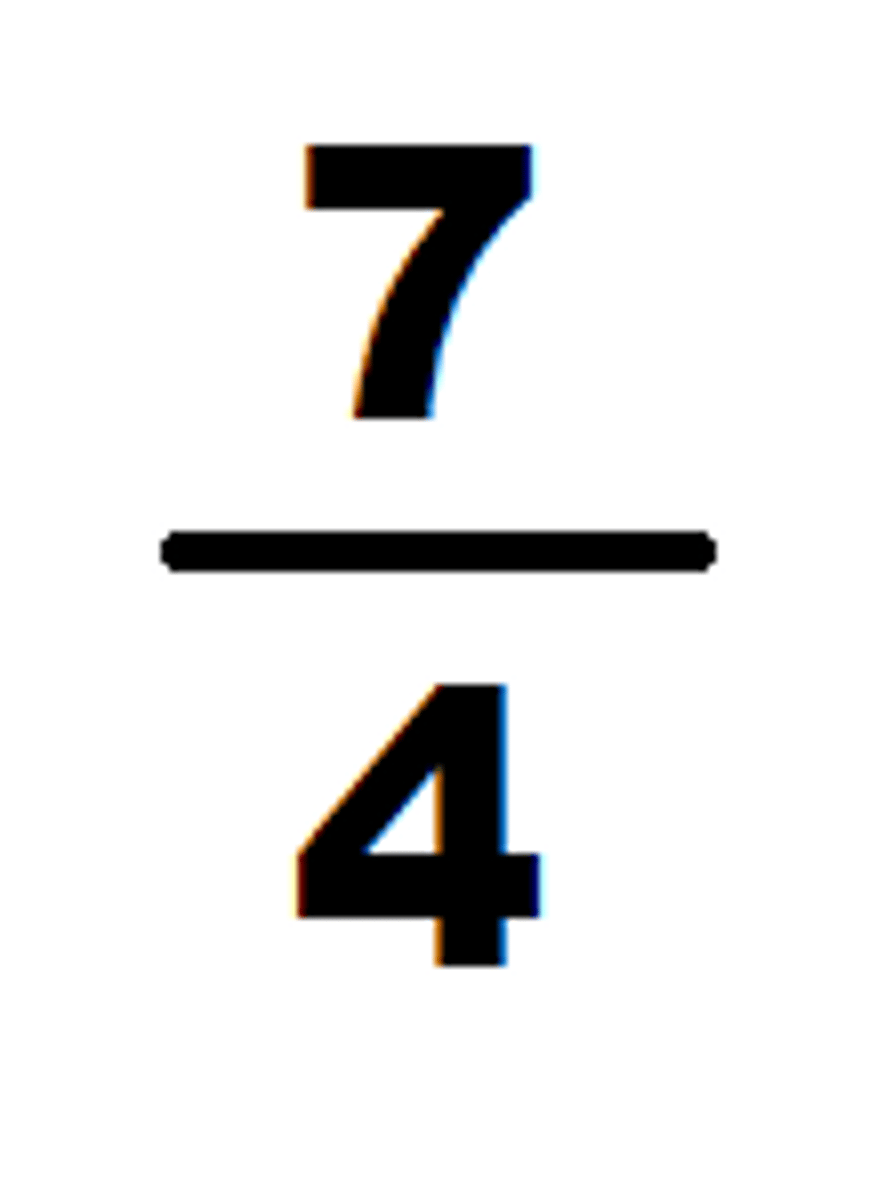
Proper Fraction

fraction whose numerator is less than its denominator

Least Common Denominator (LCD)

smallest common multiple of the denominators; the least number that both denominators divide into evenly

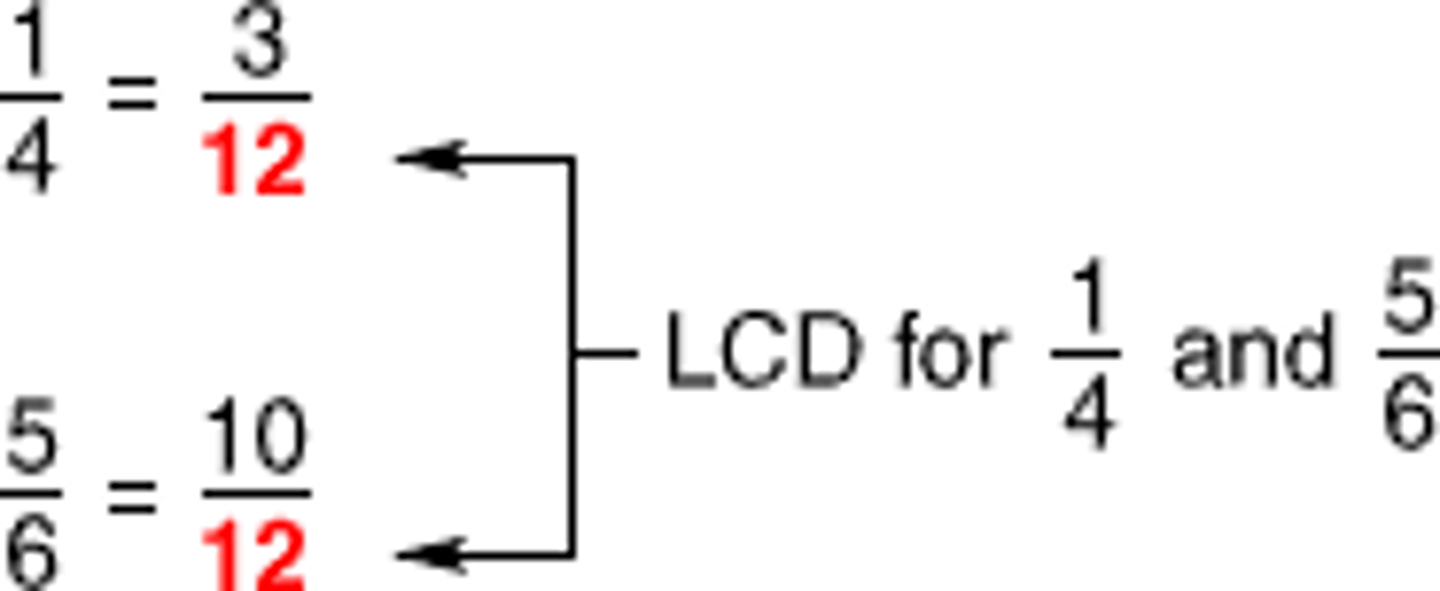
Simplified Fraction

fraction in its simplest form

Steps for Multiplying decimals

1. Set up numbers as if they were whole numbers

2. multiply the numbers

3. count the number of decimal places in the factors

4. start from the right and move the decimal the number of decimal places you counted in step 3

5. place the decimal

Steps for Dividing Decimals

1. set up the problem to be an equivalent in which the divisor is a whole number by moving the decimal in the dividend the same number of places that you moved the decimal in the divisor

2. when doing long division place the decimal in the quotient directly above the decimal point in the dividend

3. divide as if it were a whole number

Real Number

number that appears on the number line as either a rational number or an irrational number

Rational Number

any real number that can be written as a fraction, terminating decimal, or repeating decimal

Irrational Number

numbers that can be written as fractions, square roots, cube roots, and pi *not all roots are irrational

Calculating Percents

1. change written statement into a math equation

2. solve for the unknown quantity

3. rewrite the statement and makes sure that the answer is reasonable

Percent increase/decrease

Percent Increase = original value-new value/original value x 100

Percent Decrease = new value-original value/original value x 100

Fractions to Decimals

divide numerator by denominator

Decimals to Fractions

1. write the digits of the decimal number in the numerator of the fraction

2. write a number that is the power of 10 as the denominator, the number should have as many zeroes as there are decimal places to the right of the decimal

3. write the decimal fraction in simplest form

Fraction to Percent

convert fraction to decimal then multiply by 100

Percent to Fractions

1. remove %

2. write the number from step 1 in the numerator and write 100 as the denominator

3. simplify

Percent to Decimal

divide by 100 or just move decimal to the left 2 places

Decimals to Percent

multiply by 100 or just move the decimal to the right 2 places

Estimation/Approximate Values

round the numbers so that there is only on nonzero digit in each number

Reconciliation of a Checking/Savings Account

1. add up all the deposits

2. add up all the checks

3. add the total deposits amount to the previous balance

4. subtract the total checks amount from the current balance

5. add the interest amount

Calculation of Take-home Pay

add all the deductions together and subtract that amount from the beginning salary

Cost of given set of items

select items to be purchased and add the costs together

Materials & Costs of Planning an Event

1. multiply the number of people attending by each of the items they will be receiving and add those results together

2. if all the guest are receiving the same things add all the items together and multiply by the number of people

One or 2 step Word Problems with Fractions/Decimals

-when add/sub fractions remember to use common denominator

-when add/sub decimals remember to line-up decimals

Word Problems involving Percents

1. write the question as a "what part of a whole is the part?" statement

2. Then follow these steps:

-change statement to math equation (of=x, is=equals, use decimal form of %)

-solve for unknown quantity

-rewrite statement and make sure answer is reasonable

Ratios

express the relationship between two quantities, written as fractions, with an colon, or words

Proportion

states that two ratios are equal; numerators must be in the same units and the denominators must be in the same units

units of an item/units of a different item = units of an item/units of a different item *cross multiply

Rate of change

use proportions to determine the difference in completion times for a given task

Roman Numeral system

system of writing numbers using a combination of M, D, C, L, X, V, and I

Arabic Numeral System

system of writing numbers using a combination of 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Changing Roman Numerals to Arabic

1. write from left to right as a sum

2. begin with largest possible value: M=1,000, D=500, C=100, L=50, X=10, V=5, I=1

3. when I, X, or C is used to the left of a larger value, subtract its value from the larger value

Changing Arabic Numerals to Roman

1. write from left to right

2. take each place value and change to a Roman Numeral

3. I, X, and C may be written two or three times to indicate subtraction from the larger values

4. Use I, X, or C to the left of larger values to indicate subtraction from the larger values

5. V, L, and D are never used to the left of a larger value

6. V, L, and D are never used more than one time

Metric System

system of measurement based on prefixes, and every prefix responds to a power of 10; every unit has a root word

Units of the Metric System

Length - Meter (m)

Volume- Liter (L)

Weight - Gram (g)

Common Metric Prefixes

Kilo (k) - 1,000

Hecto (h) - 100

Deka (da) - 10

Deci (d) - 1/10

Centi (c) - 1/100

Milli (m) - 1/1000

Conversions between English & Metric Measurements

Length-

1 in = 2.54 cm

1 km = 1,000 m = 0.62 miles

1 m = 39.37 in

1 cm = 0.394 in

1 mile = 1,609 m

1 yard = 0.914 m

Weight-

1 kg = 2.2 lbs

1 oz = 28 g

1 lb = 0.45 kg

Volume-

1 L = 1.06 qts

1 oz = 30 mL

1 teaspoon = 5 mL

1 qt = 0.95 L

1 gal = 3.785 L

English Measurement

Length-

1 ft = 12 in

1 yd = 3 ft

1 mile = 5,280 ft

Volume-

1 cup = 8 oz

1 pint = 2 cups

1 qt = 2 pints

1 gal = 4 qts

Weight-

1 lb = 16 oz

1 ton = 2,000 lbs

Metric Measurement

Length-

1 millimeter - 0.001 meters

1 Centimeter - 0.01 meters

1 decimeter - 0.1 meters

1 meter - 1 meter

1 dekameter - 10 meters

1 hectometer - 100 meters

1 kilometer - 1,000 meters

Volume- same as length just in liters

Weight- same as length just in grams

Independent Variable

variable put into the set of data (input)

Dependent Variable

the output based on the input

Line graphs

shows changes over a period of time or compares the relationship between two quantities

Circle Graph (pie graphs)

circular graph divided into sections representing the frequency of an event

Bar graphs & histograms

used to compare frequencies of an event; histogram bars touch and bargraphs do not

Tables

useful for organizing data

Constant

quantity that does not change

Coefficient

numerical part of a term; the number that is being multiplied to the variable

Expression

one or more terms consisting of any combination of constants and/or variables

Variable

an unknown quantity in an expression, usually in the form of a letter

Like Terms

terms that have the same variable and with the same exponent

Degree

the exponent or sum of exponents of the variable of a term

Divisor

the denominator in a division problem

Dividend

the numeral in a division problem

Quotient

the answer to the division problem

Symbols & their Meanings

= - is, was, measures, becomes

< - less than, no greater than

< with line under it - less than or equal to, is at most

> - greater than, is more than

> with line under it - greater than or equal to, is at least

- - less than

+ - more than

2 - twice

Addition Principle

rule that makes it possible to move terms from one side of the equation to the other by adding opposites to each expression

Multiplication Principle

rule that makes it possible to isolate the variable in an equation by multiplying both expressions by the reciprocal of the variables coefficient

Steps to Solve Equations

1. use distributive property to get rid of any parenthesis

2. if there are fractions get rid of them by multiplying by the LCD

3. use the addition principle to move like terms together on both sides of the equation

4. use the multiplication principle to isolate the variable by multiplying both sides of the equation by the reciprocal of the coefficient of the variable

5. Check solution

Absolute Value

a numbers distance from zero on a number line

denominator

the number on the bottom of a fraction

numerator

the number on the top of a fraction

integer

a whole number

order of operations

1. parenthesis

2.multiplications and divisions

3. additions and subtractions

common denominator

a denominator that all fractions in a set can be made equivalent to so you can add and subtract

irrational number

A number whose decimal form is nonterminating and nonrepeating. Irrational numbers can't be expressed as fractions.

rational number

a number that can be expressed as a fraction

erroneous

incorrect

extraneouss

irrelevant

cartesian coordinate

a set of two or three numbers used to specify a point on a plane or space

Mean

average

median

middle value

mode

most frequent

unimodal

a symmetrical distribution with a single clear peak

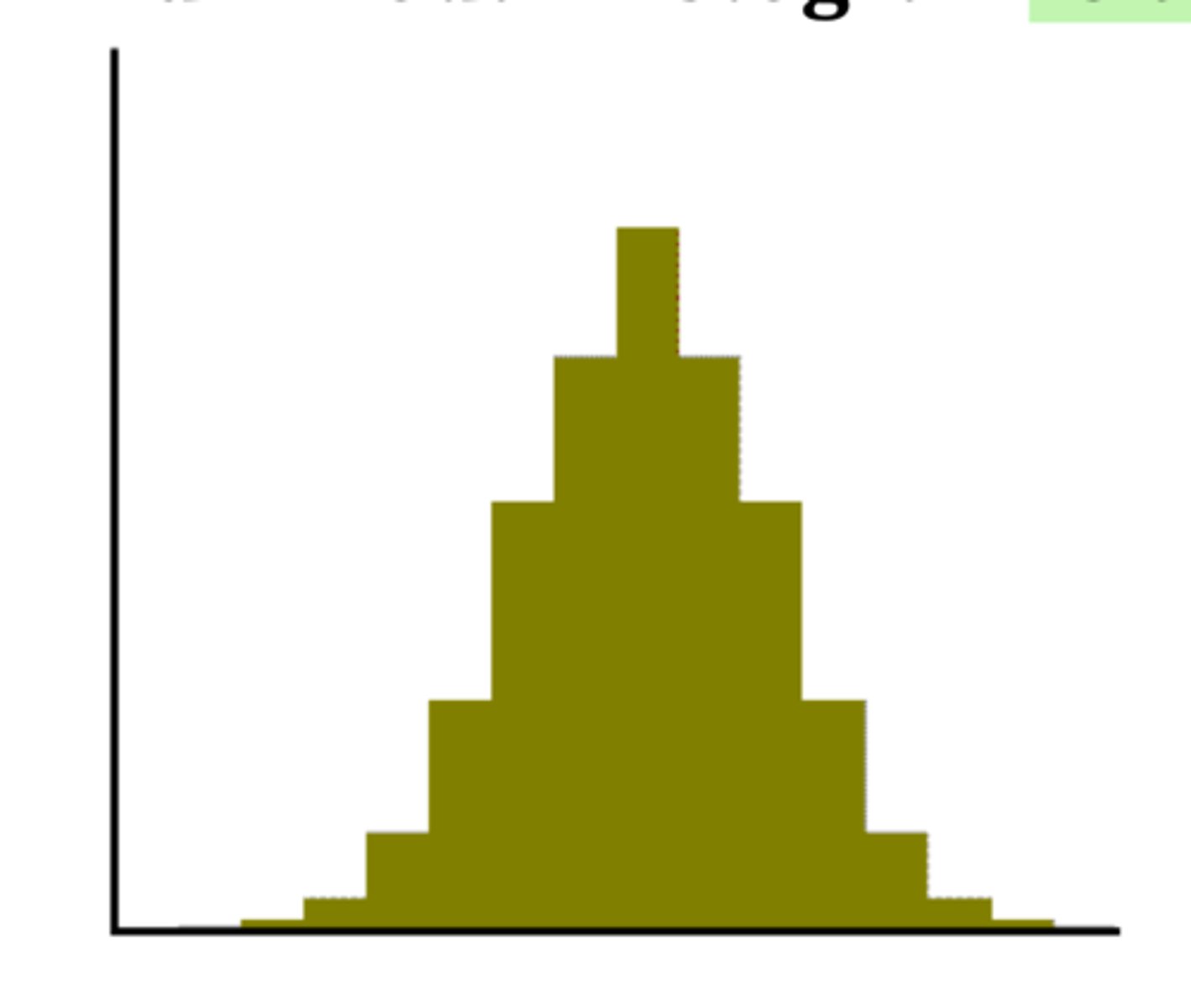
bimodal

a symmetrical distribution with two clear peaks

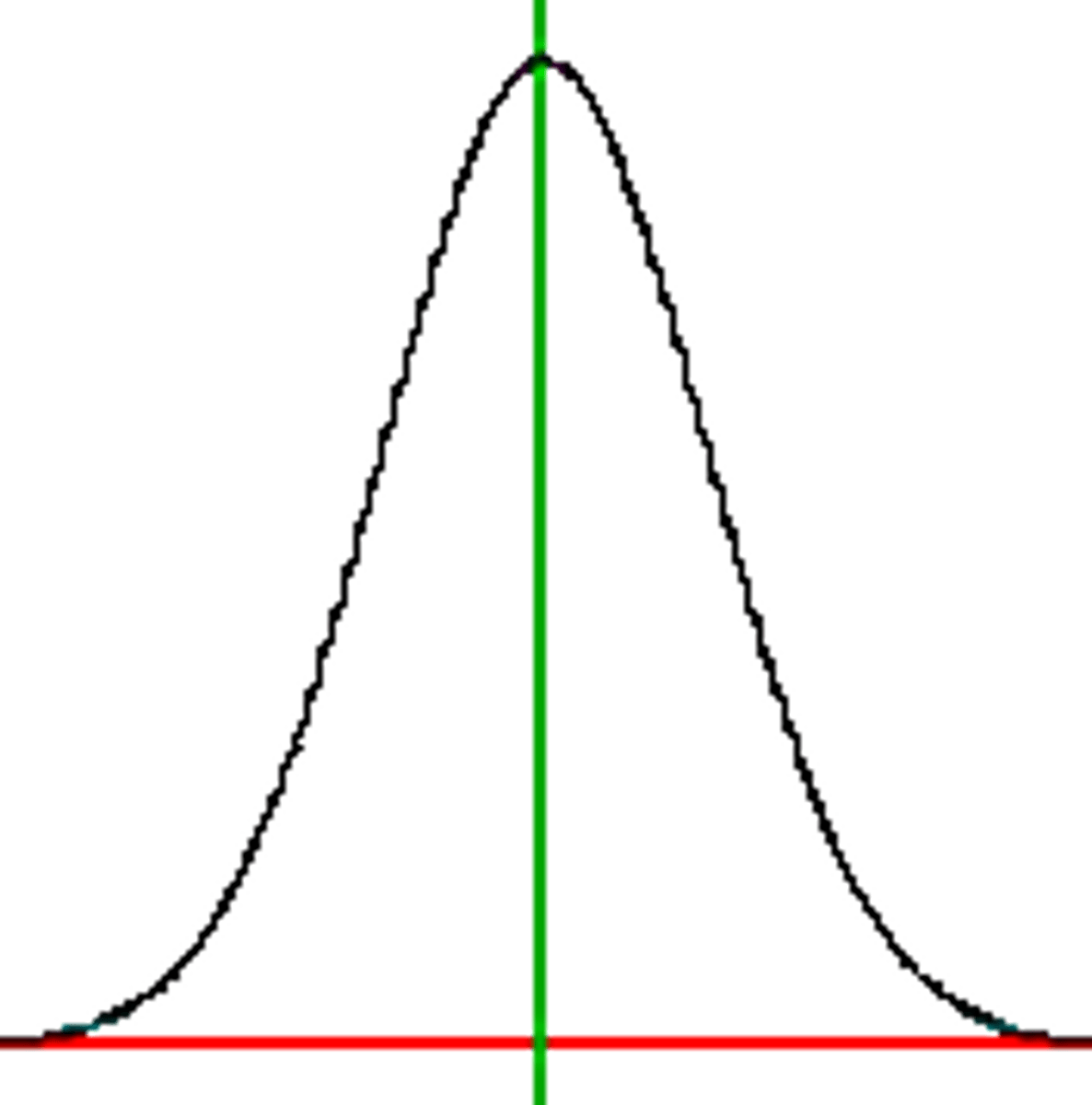
Bell shaped- normal graph

symmetrical distribution that has a singe peak at the center

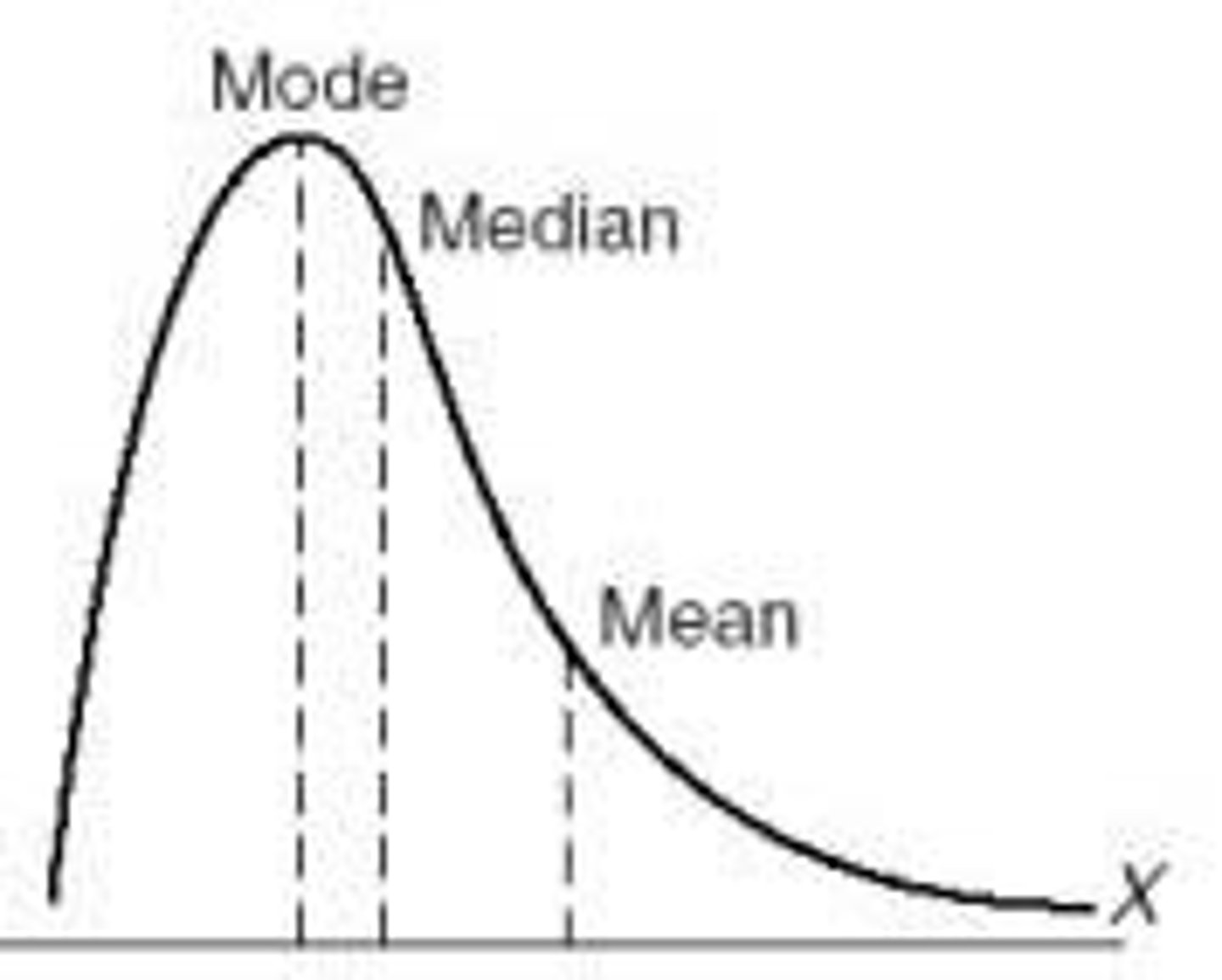
skewed right

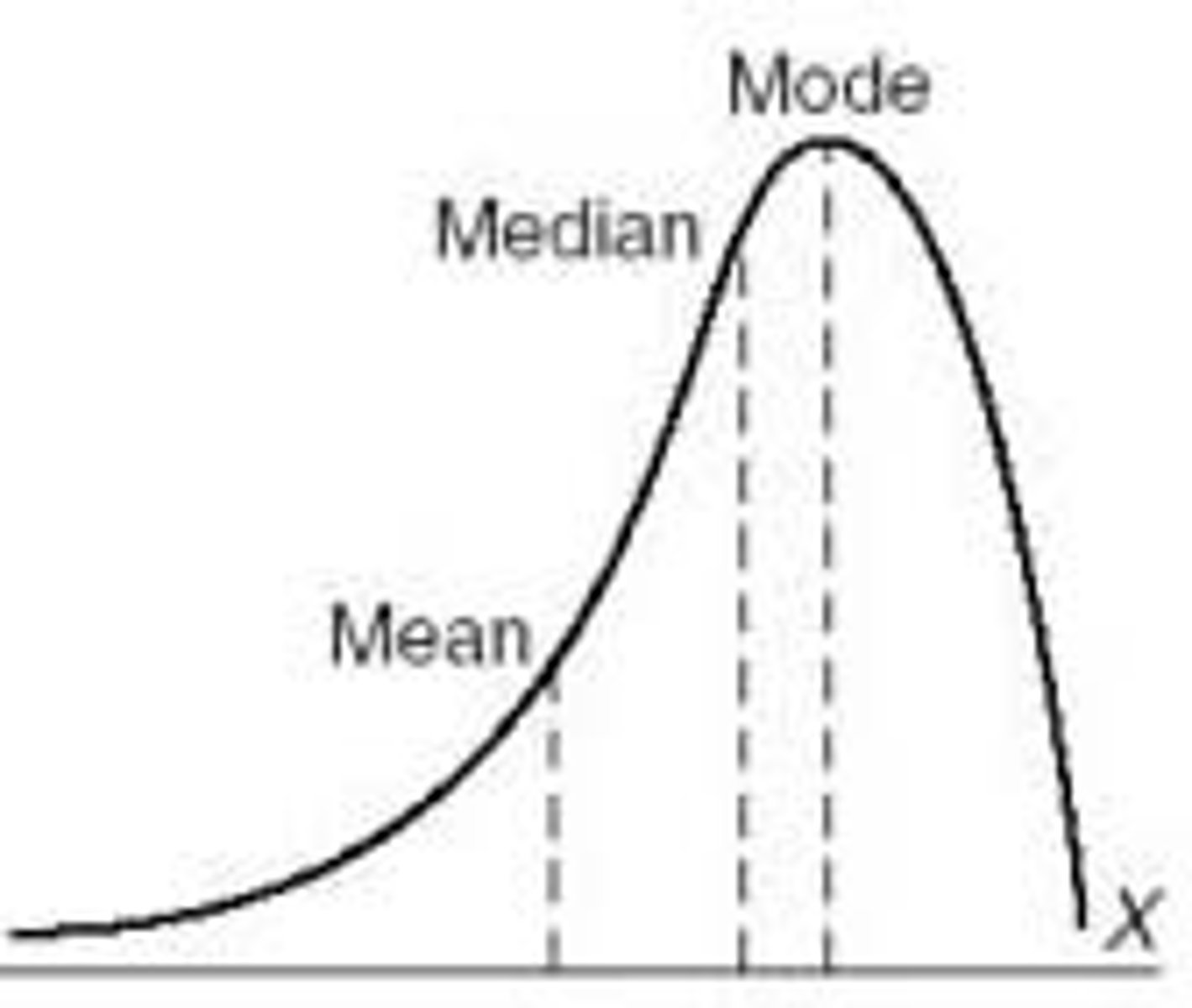
skewed left

square formula

A= l*l

rectangle formula

A= l*w

triangle formula

A= .5 baseheight

parallelogram formula

A=height*base

trapezoid formula

A= .5height (base 1+ base 2)

circle formula

A= pi* radius^2

rhombus formula

A= .5 diagonal 1 diagonal 2

perimeter

distance around a two dimensional shape

subtend

form an angel at a particular point on an arc

surface area

the total area that covers a 3D object