maths + further maths : gcse

SINE RULE (length)

a/sinA = b/sinB

SINE RULE (angle)

sinA/a = sinB/b

COSINE RULE (length)

a^2 = b^2 + c^2 - 2bcCosA

COSINE RULE (angle)

CosA = b^2 + c^2 - a^2 / 2bc

COSINE RULE:
in order to find an angle using cosine rule you need ...

all 3 lengths

COSINE RULE:
in order to find a length using cosine rule you need ...

the other two lengths and the opposite angle

SINE RULE:
in order to find an angle using sine rule you need ...

the opposite angle and another length and angle

SINE RULE:
in order to find a length using sine rule you need ...

the opposite length and another length and angle

AREA OF A TRIANGLE

1/2abSinC

SINE RULE:
ambiguos case for sine rule

sin x = sin (180 - x)

DIFFERENCE OF TWO SQAURES (D.O.T.S.)

(a + b)(a - b) = a^2 - b^2

QUADRATIC FORMULA

x = -b +- √(b^2 - 4ac)/2a

COMPLETING THE SQUARE

(x +- b/2)^2 - (b/2)^2 +- c

QUADRATIC

ax^2 + bx + c

CIRCLE THEOREM:
a + b = 180

angles in the same segment are equal

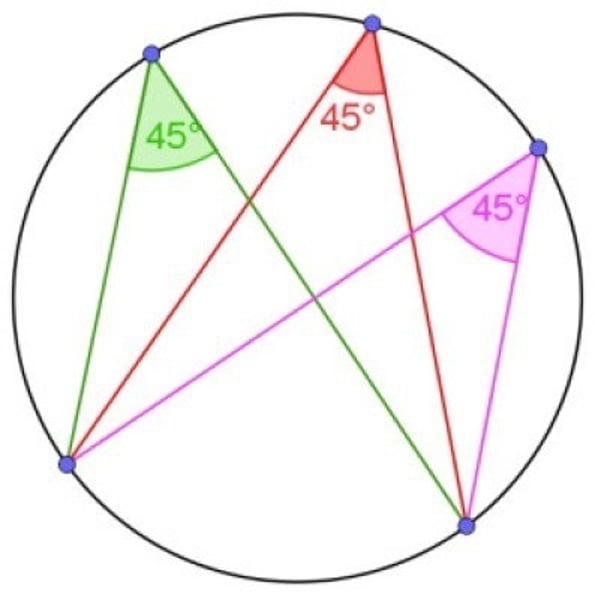
CIRCLE THEOREM:
circumference = a
centre = 2a

angle at the centre is twice the angle at the circumference

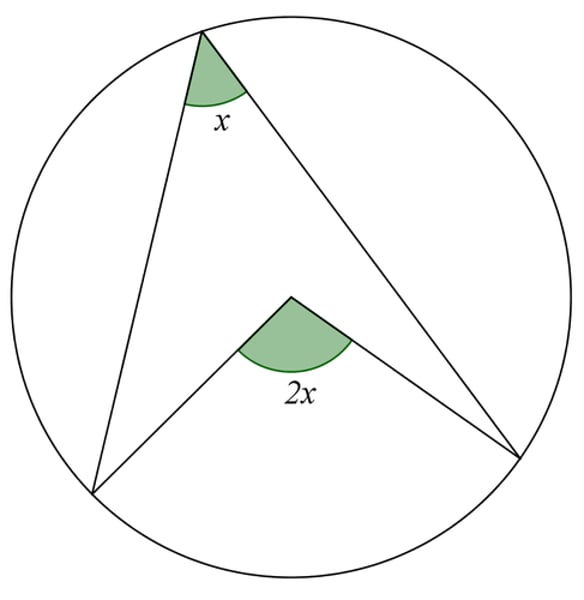
CIRCLE THEOREM:
a + c = 180
b + d = 180

opposite angles of a cyclic quadrilateral add up to 180

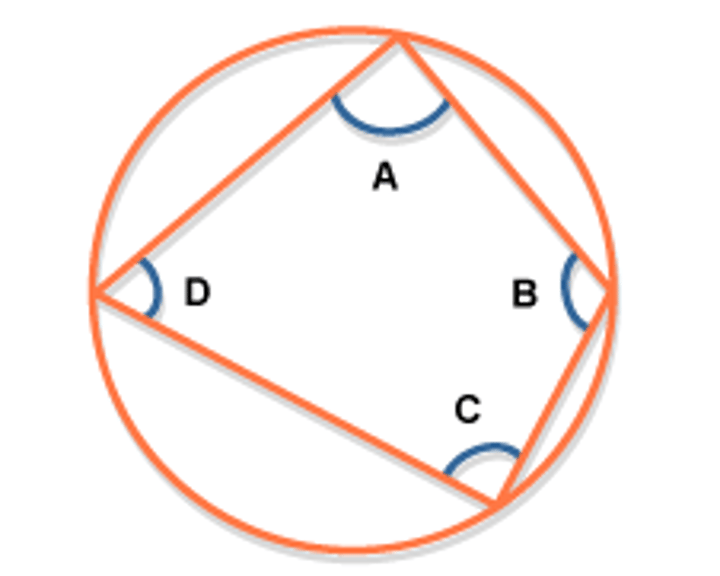
CIRCLE THEOREM:
diameter = 90

angles in a semi-circle = 90

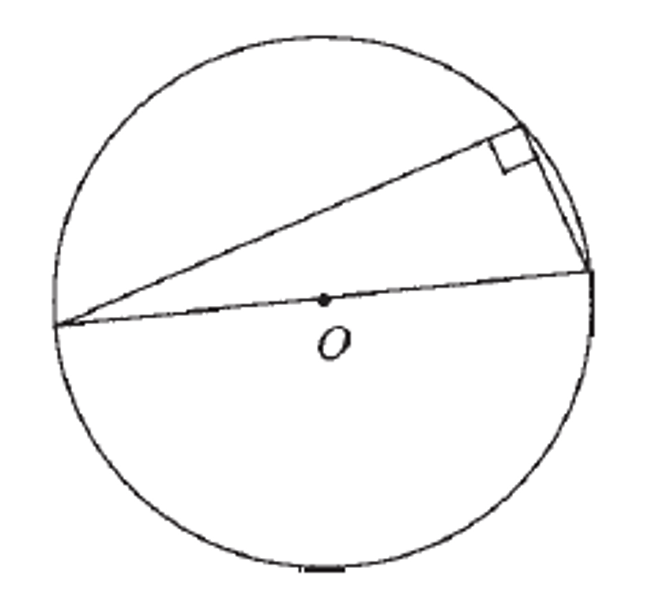
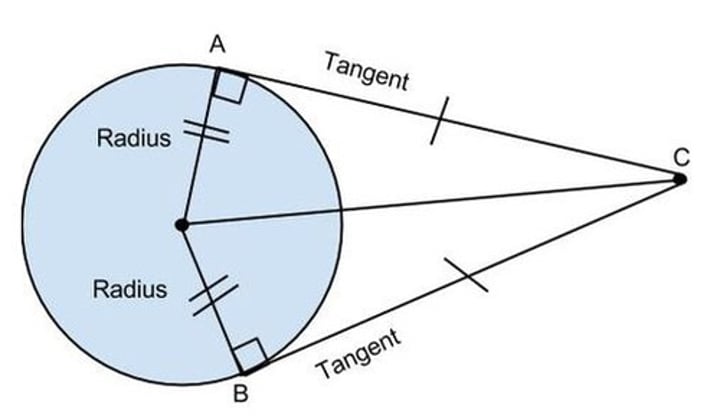
CIRCLE THEOREM:
tangent + radius = 90

a tangents meets a radius at 90

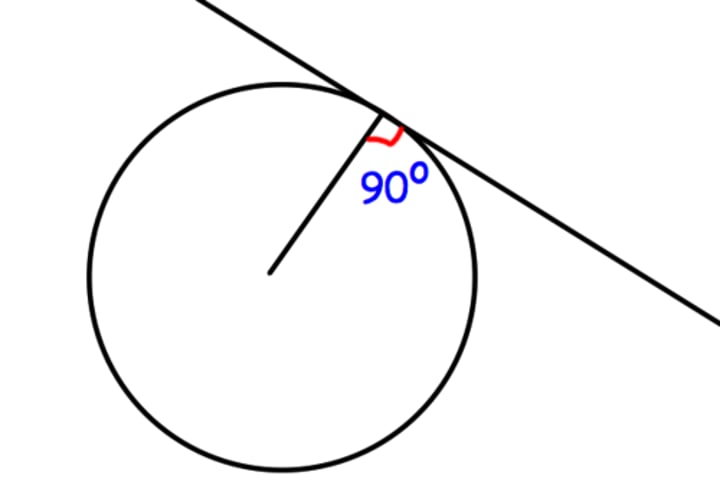
CIRCLE THEOREM:
tangent = tangent

two tangents to a circle from the same point will be equal in length

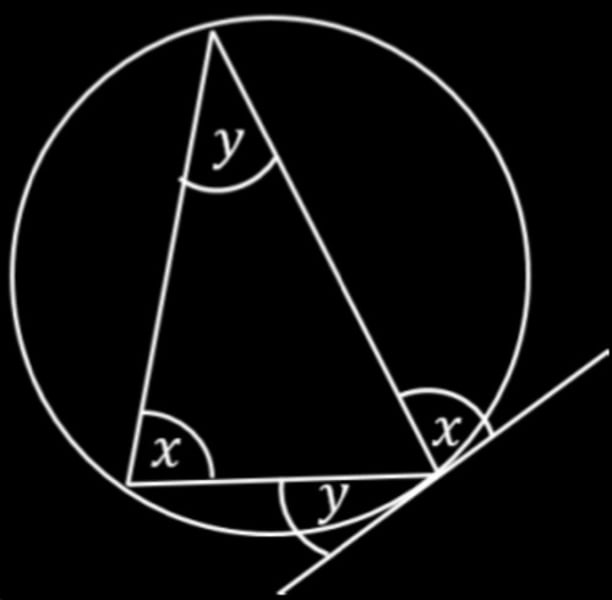
CIRCLE THEOREM:
x = x
y = y

alternate segment theorem

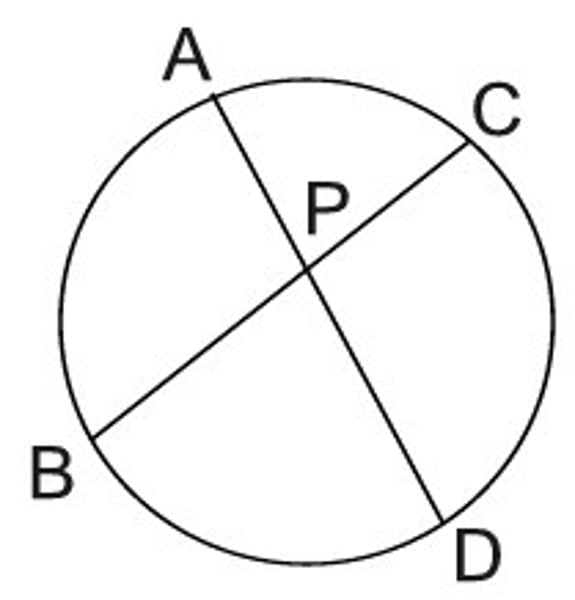
CIRCLE THEOREM:
AP x PB = CP x PD

two chords intersecting inside the circle
(P = point of intersection)

CIRCLE THEOREM:
AP x BP = CP x DP

two chords that intersect outside the circle
(P = point of intersection)

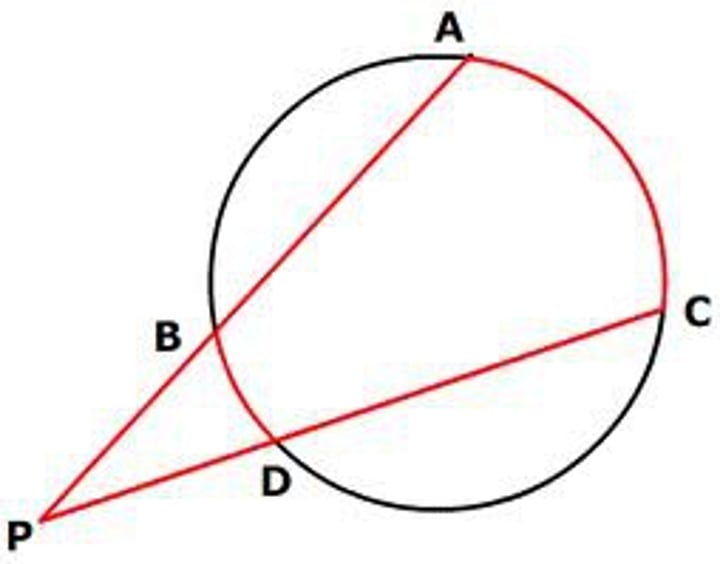
CIRCLE THEOREM:
AP^2 = CP x DP

special case for intersecting chords

BINOMIAL EXPANSION:
(x + y)^0

1

BINOMIAL EXPANSION:
(x + y)^1

1x + 1y

BINOMIAL EXPANSION:
(x + y)^2

1x^2 + 2xy + 1y^2

BINOMIAL EXPANSION:
(x + y)^3

1x^3 + 3x^2y + 3xy^2 + 1y^2

BINOMIAL EXPANSION:
(x + y)^4

1x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + 1y^4

BINOMIAL EXPANSION:
(x + y)^5

1x^5 + 5x^4y + 10x^3y^2 + 10x^2y^3 + 5xy^4 + 1y^5

BINOMIAL EXPANSION:
the sum of the powers of each term ...

add to the initial power the expression was raised to

BINOMIAL EXPANSION:
the coefficients are ...

pascal's triangle

QUARTILES:
lower quartile -LQ (Q1)

1/4n

QUARTILES:
median (Q2)

2/4n

QUARTILES:
upper quartile - UQ (Q3)

3/4n

QUARTILES:
total (Q4)

4/4n

QUARTILES:
n

the total number of values/data

CUMULATIVE FREQUENCY:
cumulative frequency

add together all the prior frequencies

CUMULATIVE FREQUENCY:
graph

class = x axis
cumulative frequency = y axis

CUMULATIVE FREQUENCY:
median on a graph

- total number of values/2
- find on y axis and find the corresponding value on the x axis

CUMULATIVE FREQUENCY:
range

IQR = Q3 -Q1

DIRECT PROPORTION

y = kx

INDIRECT PROPORTION

y = k/x

SIMILAR SHAPES:
length scale factor

k

SIMILAR SHAPES:
area scale factor

k^2

SIMILAR SHAPES:
volume scale factor

k^3

INDICIES:
law 1: a^b x a^c

a^b+c

INDICIES:
law 2: a^b / a^c

a^b-c

INDICIES:
law 3: (a^b)^C

a^bxc

INDICIES:
law 4: a^-b

1/a^b

INDICIES:
law 5: (a/b)^-c

b^c/a^c

INDICIES:
law 6: a^0

1

INDICIES:
law 7: a^1

a

INDICIES:
law 8: a^1/b

b√a

INDICIES:
law 9: a^b/c

(a^1/c)^b = (c√a)^b

INDICIES:
law 10: (ab)^c

a^c x b^c

SURDS:
law 1: √a x √b

√axb

SURDS:
law 2: √a / √b

√a/b

SURDS:
law 3: √a x √a

a

SURDS:
rationalising: 1/√a x √a/√a

√a/ a

SURDS:
rationalising: 1/√a + √b x √a-√b/√a-√b

√a-√b / a-b
D.O.T.S.

INEQUALITIES:
x < y

y is greater than x

INEQUALITIES:
x > y

y is less than x

INEQUALITIES:
x ≤ y

y is greater thinner equal to x

INEQUALITIES:
x ≥ y

y is less than or equal to x

INEQUALITIES:
≥ or ≤ on a number line

solid dot

INEQUALITIES:
< or > on a number line

open dot

PRODUCT RULE FOR COUNTING:
¡

factorial

HISTOGRAMS:
frequency (f) , class width (cw) , frequency density (fd)

fd = f / cw

HISTOGRAMS:
graph

x axis = class
y axis = frequency density

TRIGONOMETRY

SoH CaH ToA

3D TRIGONOMETRY

a = √x^2+y^2+z^2

EQUATION OF A CIRCLE:
to find the midpoint

(x1 + x2 / 2 , y1 + y2 / 2 )

EQUATION OF A CIRCLE:
distance between two points

√(y2-y1)^2 + (x2-x1)^2

EQUATION OF A CIRCLE:
with the centre (0 , 0)

x^2 + y^2 = r^2

EQUATION OF A CIRCLE:
with the centre NOT at (0 , 0)

(x-a)^2 + (y-b)^2 = r^2

CIRCLE:
area

pi r^2

CIRCLE:
circumference

2 pi r

CIRCLE:
length of arc

x/360 x 2 pi r

CIRCLE:
area of sector

x/360 x pi r^2

CIRCLE:
area of segment

area of sector - area of triangle
(x/360 x pi r^2) - 1/2r^2Sinx

PROBABILITY:
the "and" rule

p(A , B) = p(A) x p(B)

PROBABILITY:
the "or" rule

p(A or B) = p(A) + p(B)

BOUNDS:
upper bound , addition

UB + UB

BOUNDS:
upper bound , subtraction

UB - LB

BOUNDS:
upper bound , multiplication

UB x UB

BOUNDS:
upper bound , division

UB / LB

BOUNDS:
lower bound , addition

LB + LB

BOUNDS:
lower bound , subtraction

LB - UB

BOUNDS:
lower bound , multiplication

LB x LB

BOUNDS:
lower bound , division

LB / UB

PERCENTAGES:
general formula (simple interest)

oa x m = na

PERCENTAGES:
compound interest

oa x m^n

PERCENTAGES:
percentage change

na-oa / oa x 100

TRANSFORMATIONS:
rotation

- centre point
- direction of rotation
- angle of rotation

TRANSFORMATIONS:
refelction

- line of reflection

TRANSFORMATIONS:
translation

- vector

TRANSFORMATIONS:
enlargement

- centre of enlargement
- scale factor

EQUATIONS OF LINES:
general equation

y = mx + c

EQUATIONS OF LINES:
gradient

(y2 - y1) / (x2 - x1)