2.1 data structures and abstract data types

data structures

“containers” to store information in of which there are many different types

static vs dynamic data structures

static structures are fixed in size, while dynamic structures can change in size

static and dynamic structures and memory

static structures have a fixed amount of memory allocated to them at compile time while dynamic data structures will have memory allocated and de-allocated as the program executes

if values are added to full static structures, an overflow error will occur

static structures pros and cons

pros:

-adding data won’t cause an overflow error unless they’re full as data is already allocated to them

-faster to access as they are usually allocated one continuous block of memory

cons:

-less memory efficient as they are usually allocated a lot of unused memory

-adding data causes an overflow error if they’re full

dynamic structures pros and cons

pros:

-more memory efficient as all memory allocated to them will be in use

-no limit to their size apart from the computer’s processing power

cons:

-slower to access as they are often allocated many small blocks of memory that must be kept track of and switched between

-can overflow if an excessive amount of data is added

arrays

an indexed set of elements of the same data type

lists are used as arrays in python

single vs multi-dimensional arrays

single-dimensional arrays contain a set of singular elements, multidimensional arrays contain a set of arrays

field

a single unit of data storage in a computer file

record

a row of fields in a data storage file

files

collections of data and instructions stored as one item in a computer

abstract data structures

data structure types that don’t exist in their own right but can be created using data structures (and possibly code to process them) to store information in a way that might be more useful to the program

queues

an abstract data type- a FIFO structure like a real life queue. can be linear, circular or priority

have front and rear pointers

linear queues

elements can only be inserted at the rear, and cannot be moved down the list to make space for more elements. pointers move down the list as elements are added and removed

pointers cannot move back to the front of the queue, meaning once the last space is filled no new elements can be added even if there is free space

less memory efficient than circular queues

circular queues

elements can only be inserted at the rear, and cannot be moved down the list to make space for new elements. pointers move down the list as elements are added and removed

pointers can move from the back of the queue to the front so that elements can always be inserted as long as there is free space

more memory efficient than linear queues

priority queues

queues where items are assigned a priority level, and each priority is essentially its own queue. items with higher priorities are always removed before items with lower priorities

stacks

an abstract data type- an LIFO structure much like a real life stack

have only top pointers

lists

a list of values

in python:

list = [ val1, val2, val3 ]

graphs

an abstract data structure used to represent complex relationships between elements, much like a real life graph with elements connected by lines

graphs consist of nodes(vertices) joined by edges(arcs) which may be directional or weighted(given a value)

adjacency matrices

a matrix showing relationships between nodes in a graph. to check for an edge between two nodes, the point on the row and column corresponding to the two nodes is checked

these matrices can either include 0s(no edge) and 1s(edge) or values(the weight of the edge) and arbitrarily large values(no edge)

undirected adjacency matrices will have diagonal symmetry, and all adjacency matrices will have a row of 0s or ALVs running diagonally where the row and column correspond to the same node

adjacency lists

a list showing the relationships between nodes in a graph. each index represents one node and contains a list of other nodes it is connected to

adjacency matrices vs lists

-adjacency lists take up less memory as they only record where an edge exists, while matrices must specify if an edge exists or not

-adjacency matrices are quicker to search as the indices correspond to both nodes, while adjacency lists are slower to search as one node must be searched for the presence or absence of the other node

trees

connected, undirected graphs with no cycles

root nodes are (optional) nodes that all other nodes stem from, and nodes with no children are called leaf nodes

binary trees

rooted trees where each node has no more than two child nodes and no more than one parent node

uses for rooted trees

-to represent family trees

-to represent a file system

-used by AI to make decisions

hash tables

store key-value pairs based off of a hashing algorithm. the values are stored in the position corresponding to their hash

very efficient but two values can have the same hash causing a collision. rehashing solves this problem

rehashing

a procedure is used to find an available position for an item in a hash table if the position for its hash is already taken to avoid collision

this procedure can be anything- for example moving it to the next unoccupied position

hashing

a hashing algorithm takes an input and returns a hash, it cannot be done in reverse to figure out the input value

dictionaries

a collection of key-value pairs, values can be accessed using the associated key

ex in python

dict = { key1:val1, key2:val2, key3:val3 }

vectors

a way of representing something’s position in space

representing vectors

as a list of numbers e.x. [2, 3, 4]

as a point in space e.x. (2,3,4)

as an n vector over ℝ written as ℝ^n e.x. ℝ³ (R being real numbers, n being the number of dimensions represented)

as a function that maps indices to the corresponding value e.x. a dictionary dict = { 0:2, 1:3, 2:4 }

vector mathematics

vector + vector = add each coord

vector x scalar = multiply every coord by the scalar

dot prod. of 2 vectors = multiply each coord and add them to create a scalar. this can be used to find the angle between two vectors

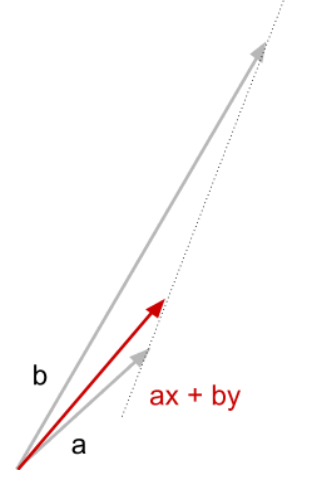
convex combination of 2 vectors

the convex combination of vectors a and b is ax + by, where x and y are decimal numbers that add to one

the convex combination ends on the line that joins the ends of a and b, the point where it ends splits the line proportionally to x and y

(i.e. if x is 0.25 and y is 0.75, the CC ends 75% of the way along the line from x to y)