stats - exam 3

repeated measures design

evaluates the mean difference between two measurements taken from a single sample

repeated measures qualities

• each participant completes both the congruent and incongruent condition

• no control group

• two scores per individual

• different scores are used to determine the effects of the conditions

in a repeated measures experiment, each participant completes _____

the congruent and incongruent condition

in a repeated measures experiment, the control group is _____

non-existent

repeated measures alternate terms

within-subject, related samples, or dependent samples designs

in repeated measures, a hypothesis is tested about the _____ between two measurements using a single sample

population mean difference

in repeated measures, a hypothesis is tested about the population mean difference between _____

two measurements in a single sample

in repeated measures, a _____ must be computed

difference score for each individual

equation for difference score for each individual

D = X2 - X1

X1

the subject’s score at the first measurement

X2

the subject’s score at the second measurement

repeated measures requires _____ subjects than an independent measures design

less

in repeated measures, individual differences in performance from one participant to another are _____

eliminated

repeated measures designs reduces the _____ (2)

variance between subjects + estimated standard error 

since repeated measures reduces the variance between subjects and estimated standard error, _____ is ultimately increased

power

repeated measuresis well suited for examining _____

changes that occur over time

disadvantages of using repeated measures

testing effects, floor / ceiling effects

testing effect

exposure to the first condition may influence scores in the second condition

floor effect

when an individual’s score is at a minimum in the first score, meaning they can only improve in the second

ceiling effect

when an individual’s score is at a maximum in the first score, meaning they can only worsen in the second condition

repeated measures hypothesis testing step 1

state the hypothesis and select the a level

to measure effect size in repeated measures, _____ can be used

cohen’s d + r²

in repeated measures, the _____ of difference scores is used to test hypotheses about the _____ of different scores

sample + population

null hypothesis in repeated measures (two tailed)

there is no consistent or systematic difference between the two conditions

in a repeated measures null that is non-directional / two tailed,

some participants may show a positive or negative difference

but on average, _____

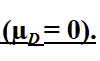
alt hypothesis in repmes (two tailed)

there is a systematic difference between conditions that produces a non-zero mean difference 

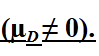
the alternative hypothesis is that the _____ represents a true population mean difference

sample mean difference

the alternative hypothesis is that the sample mean difference represents a _____

true population mean difference 

the alternative hypothesis is that the _____ represents a _____

sample mean difference + true population mean difference

in repmes, all calculations are done with the sample of difference scores

obtained difference / estimated standard error of

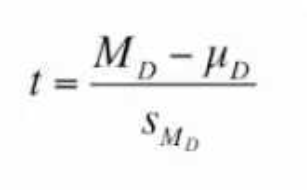
in repmes, all calculations are done with the sample of difference scores

theoretical numerator of repmes

md-ud

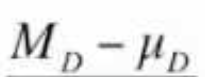
hypothesized population difference

mu_d

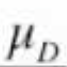
since the repmes null is that μ=0, the numerator would be equivalent to _____

M_D

the estimated standard error for the M_D

S_MD

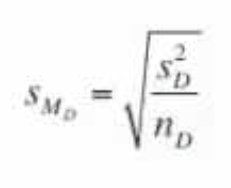
repmes is used when _____ (3)

μ and σ are unknown + μ cannot be estimated + one sample is being examined

in repmes, the sample of difference scores is used to _____

test hypotheses about the population of difference scores

repeated measures designs _____ power

increases

repeated measures designs increase power, which _____ the standard error

decreases

M_D equation

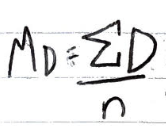
S_MD equation

S_MD

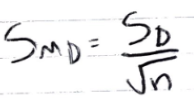
cohen’s d

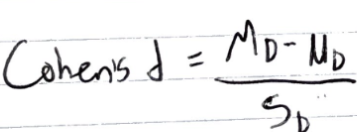
r² equation

r²

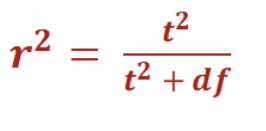
repeated measures - hypothesis testing -  step 2 

locate the critical region

degrees of freedom for the repeated measures t-test 

n-1

repeated measures - hypothesis testing -  step 3

compute the test statistic

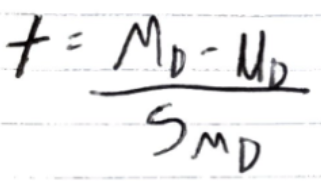
calculations go in order of _____ (4)

M_D → S_D → S_MD → t

repeated measures t-test looks at the _____.

mean difference between two measurements

repeated measures - hypothesis testing -  step 4

make a decision after comparing t-value to critical value

SPSS output: M

mean

SPSS output: N

sample size

SPSS output: s

standard deviation

SPSS outputs for upper table

M (mean), N (sample size), s (standard deviation)

SPSS output (lower table)

mean = M_D

S_D = std. deviation

SMD = std error mean

t stat = t

df = df

p value = sig 2 tailed

ANOVA

analysis of variance

ANOVA is a hypothesis testing procedure used to evaluate _____

mean differences between 2 or more populations

the purpose of ANOVA is similar to _____

t-tests and they would yield the same results.

ANOVA can examine ______

more than 2 groups simultaneously

ANOVA helps prevent _____ when comparing two or more population means 

type I error

ANOVA automatically adjusts for the _____

effect that testing multiple hypothesis has on type I errors

in ANOVA, the IV that splits participants into groups is called a _____

factor

in ANOVA, the individual conditions or values that make up a factor are called _____

levels

the # of levels are indicated by the symbol __

k

ANOVA can be used with multiple factors at the same time

different groups of people that can be put into , control, one treatent type, another treatment type > these three are different groups that are grouped into one treatment types meaning it is one level

the test statistic for ANOVA

F-ratio

F-ratio is a sample’s ____:_____

systematic variance : random variance

in ANOVA, sample variances are equivalent to _____

mean squares

in ANOVA, mean squares are referred to as _____

MS values

MS_between is displayed at the _____

top of the F-ratio

MS_between refers to _____

the signal / systemic variability

MS_between measures _____

the size of the difference between each level’s sample mean

MS_within is displayed at _____

the bottom of the F-ratio

MS_within refers to _____

the noise / random variability

MS_within measures _____

the magnitude of differences expected without any effects of the IV

MS_within measures the variability that exists _____

inside each of the treatment levels

the F-ratio has the same basic structure as the _____

the independent measures t-statistic

F-ratio

F = MS_between / MS_within

MS_between

obtained mean differences, including treatment effect

MS_within

differences expected by change without treatment effects

example: what equations must be used?

suppose a factor has three levels, each with n=25. the level means are M₁=1 M₂=2 M₃=3. the three level means are different / variable. by computing the variance of the means (MS_between), we can test the size of the difference. 

MS_between=SS_between / df_between

SS_between= n(SS_means)

df_between= k-1

MS_between can be caused by two sources:

effects of the IV & chance of sampling error

chance of sampling error in terms of MS_between

if there is no effect of the IV at all we would still expect some differences in the DV values between levels due to random, unsystematic sampling error

effects of the IV in terms of MS_between

could cause the mean for one level to be higher or lower than that for another

in an F-ratio, the signal represents the _____

magnitude of the difference between means

in an F-ratio, the noise represents the _____

magnitude of the random differences expected without any of the effects of the IV

MS_between represents the variability caused _____

by the IV

MS_between can be understood as the signal because it _____

reflects the systematic differences between group means.

MS_within represents the variability ______

within groups due to random error or individual differences

MS_within can be understood as the noise because it _____

reflects the expected variation that would occur by chance, even without an effect from the IV

if the MS_within is smaller than the MS_between, the f value will be _____

greater

the greater the f value, the realer the _____

difference

if the f-value is greater, this mean the calculation is _____ due to chance.

not

ANOVA null

all μ’s are equal

ANOVA alt

there is at least one mean difference

all hypotheses in ANOVA are _____

non-directional

F is a ratio of ______

variances

since F is a ratio of variances, we can never have a _____

negative F

variances cannot be _____

negative

all hypothesis in ANOVA are non-directional because variances _____

cannot be negative 

in the ANOVA distribution, there is / are _____ tail(s)

one