Matrices 2.a et 2.b

Definition of Linear Independence

A set of vectors X1,X2,...,XkX_1, X_2, \dots, X_kX1​,X2​,...,Xk​ is said to be linearly independent if none of the vectors can be written as a linear combination of the others.

ex: V= 2K + 3W

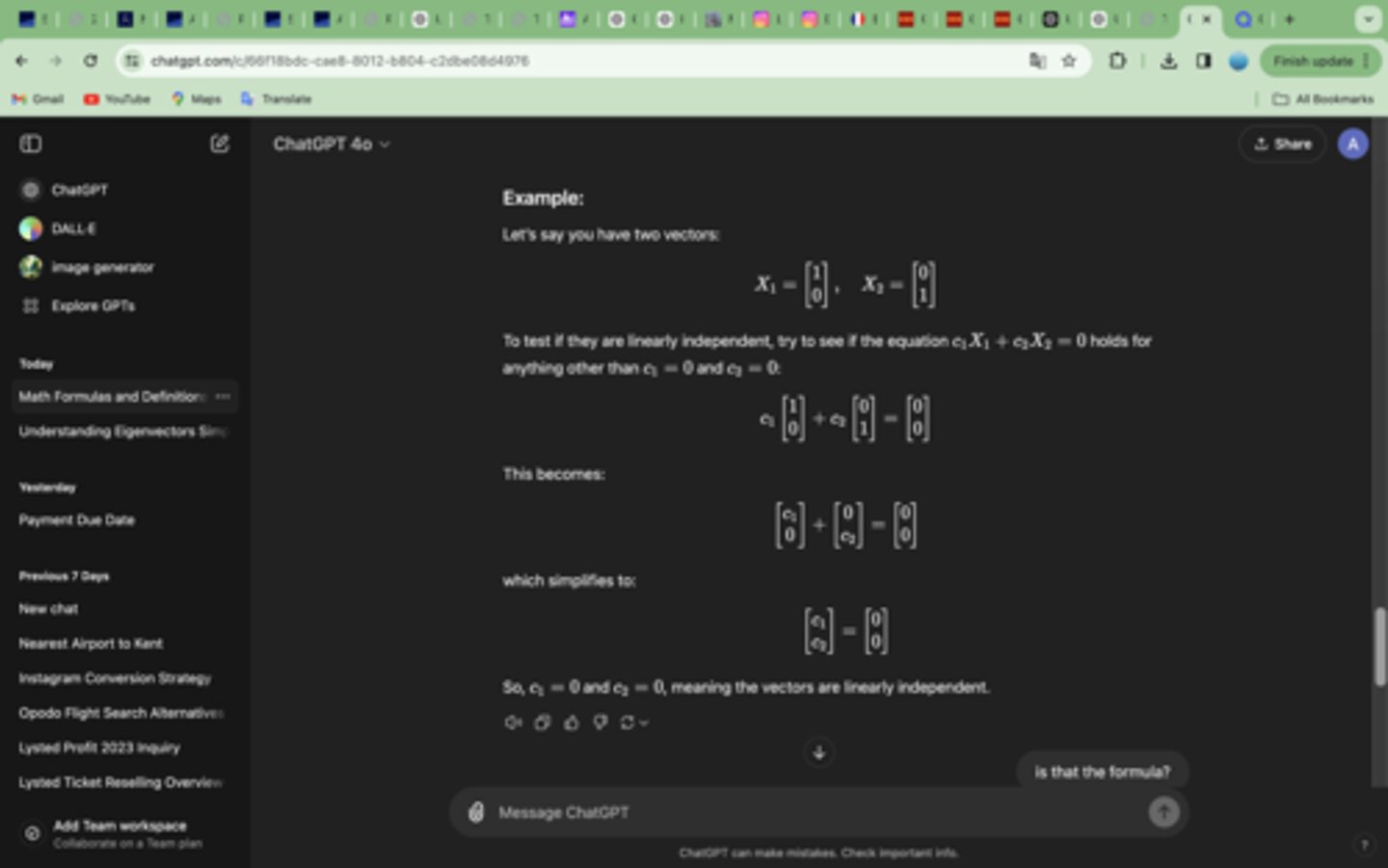
Formula to test Linear Independencebetween 2 vectors

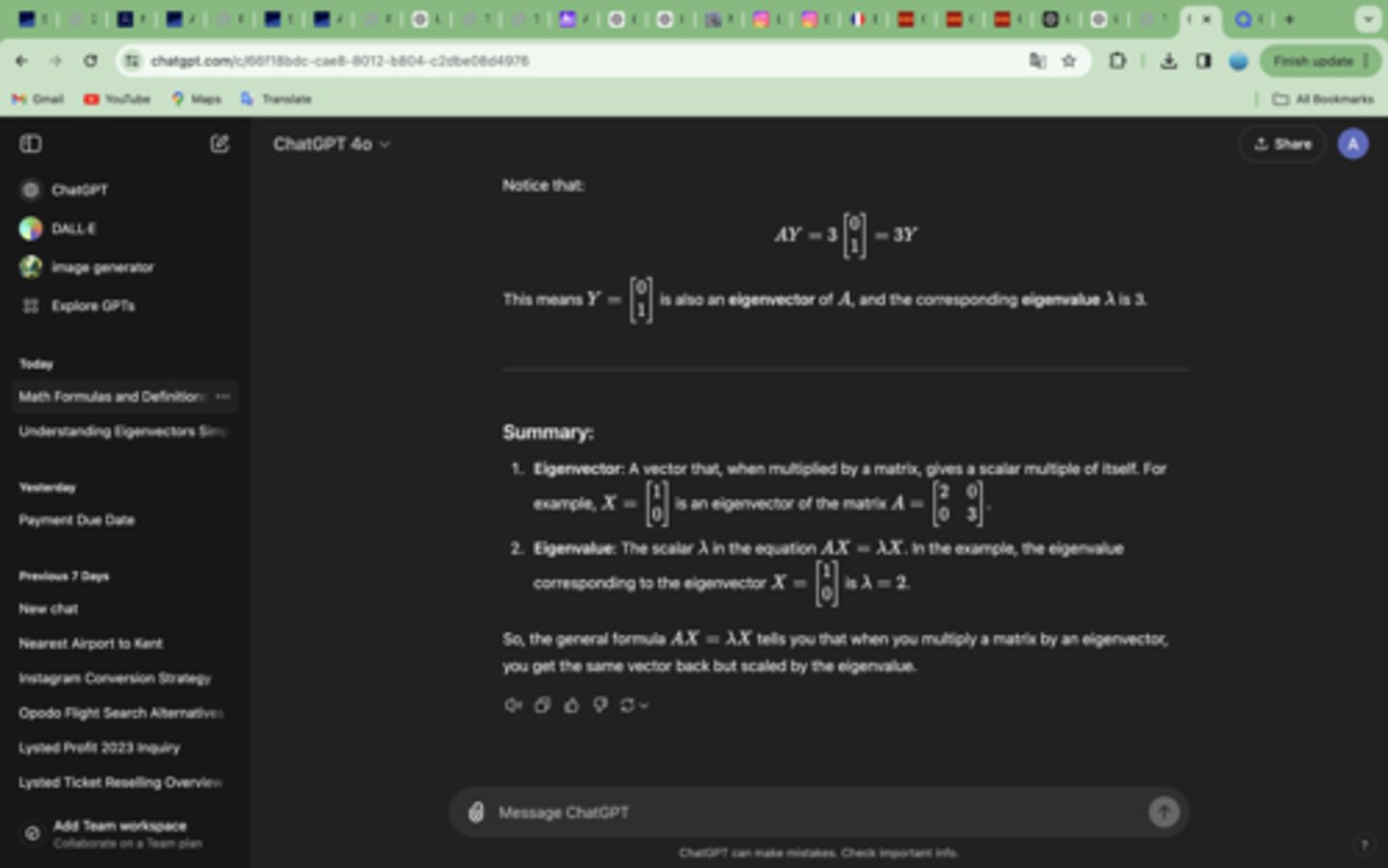
Definition of Eigenvector and Eigenvalue

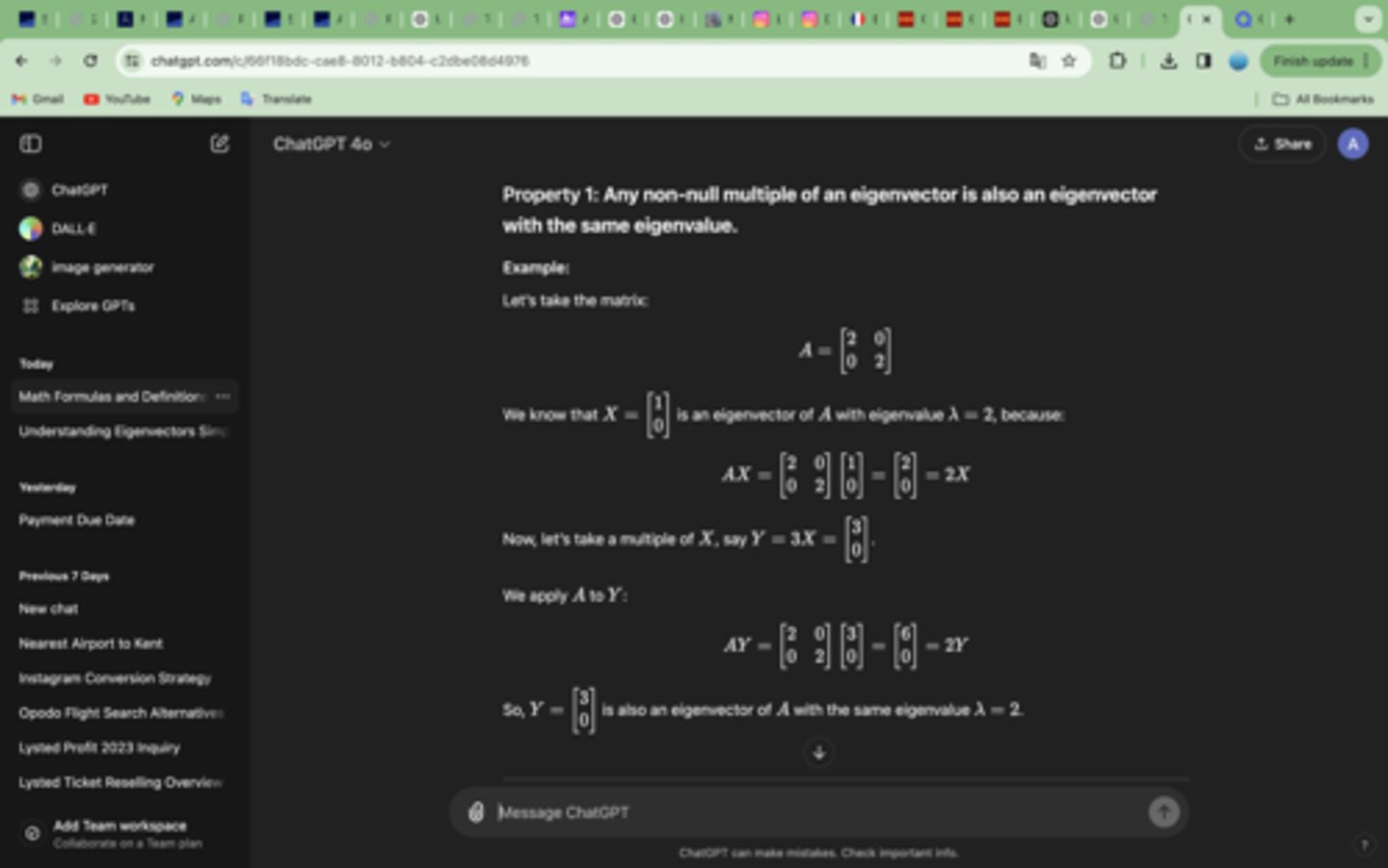
1. Any non-null multiple of an eigenvector is also an eigenvector with the same eigenvalue.

2. Eigenvectors corresponding to distinct eigenvalues are linearly independent.

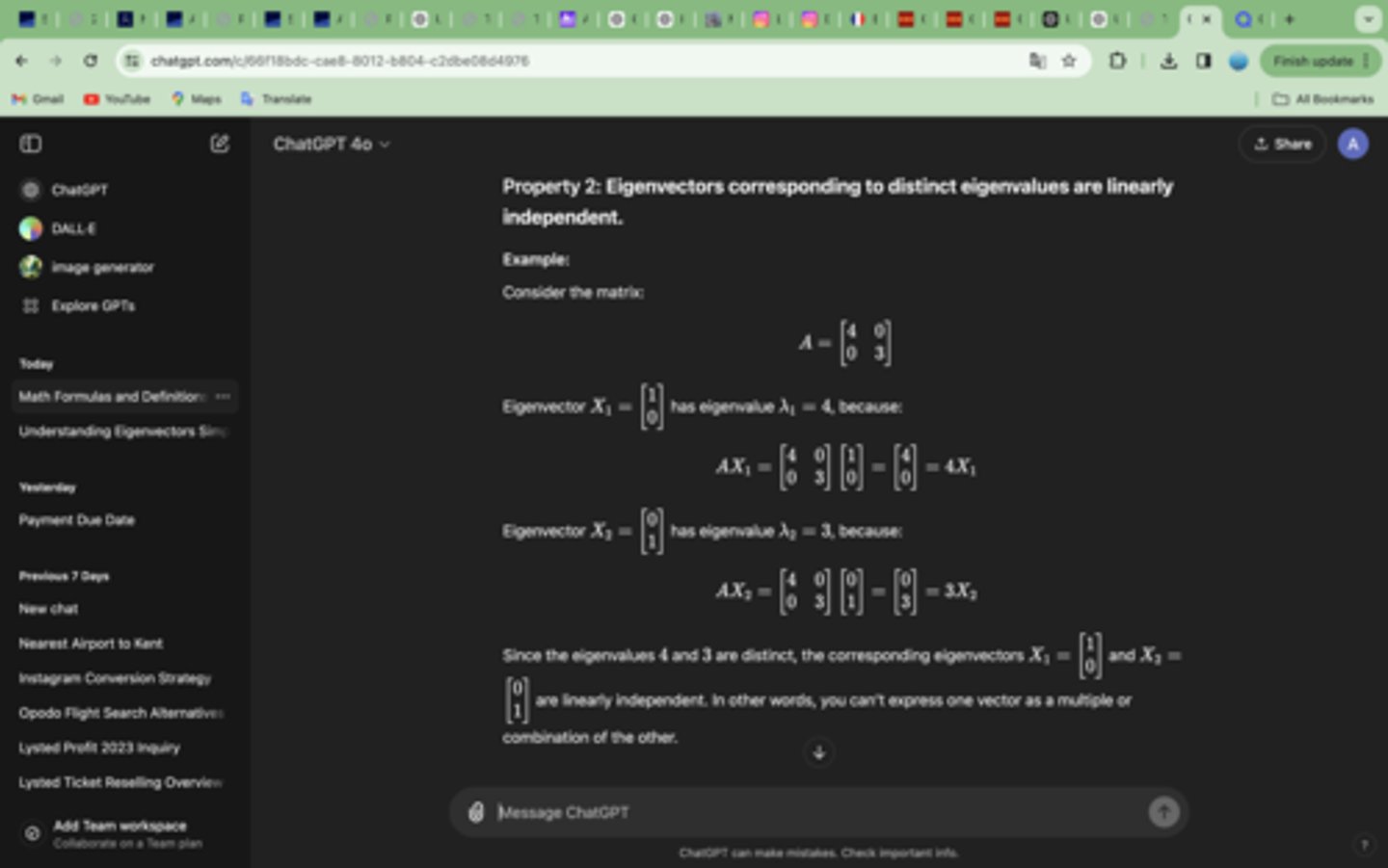
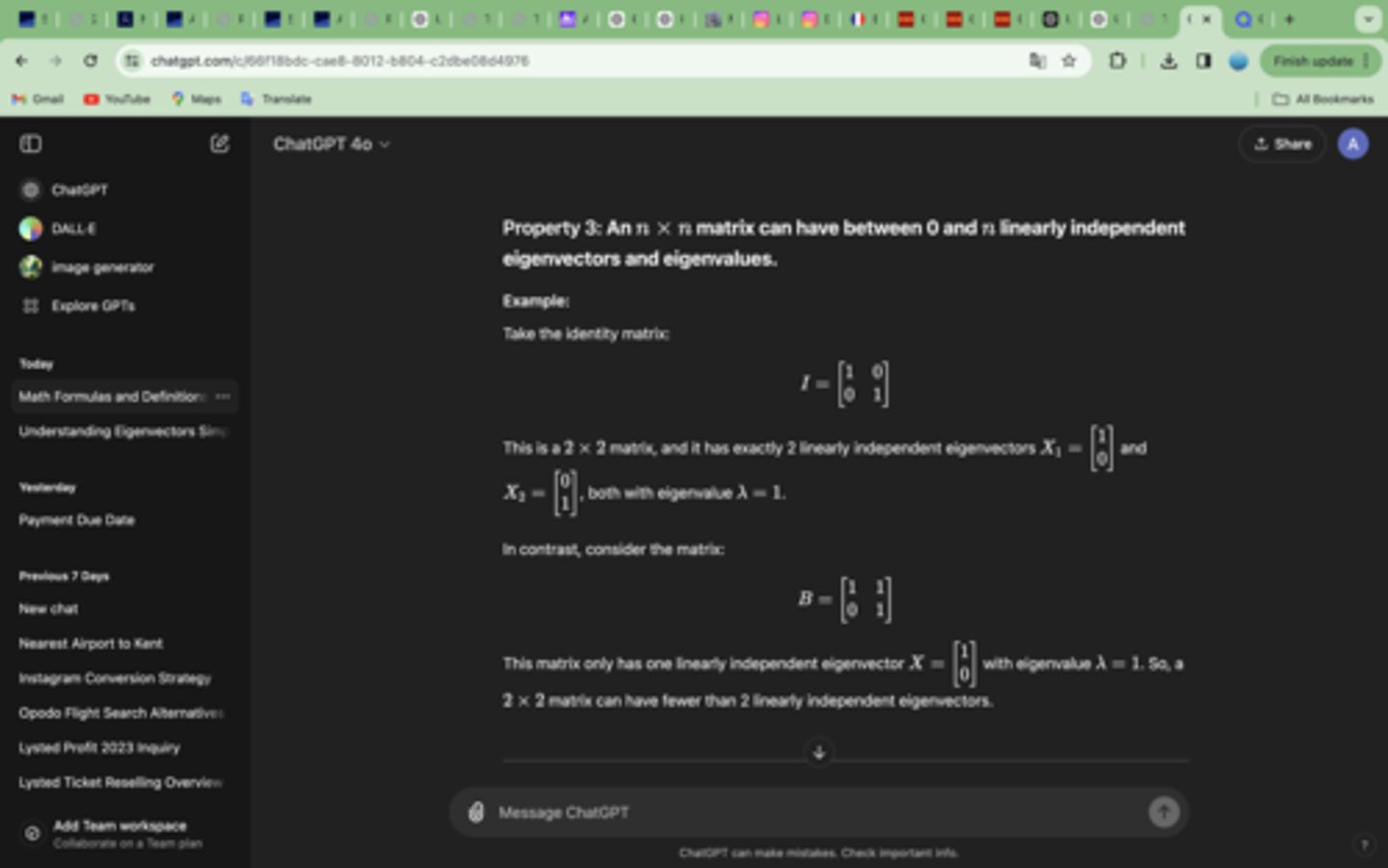
An n×n matrix can have between 0 and n linearly independent eigenvectors and eigenvalues.

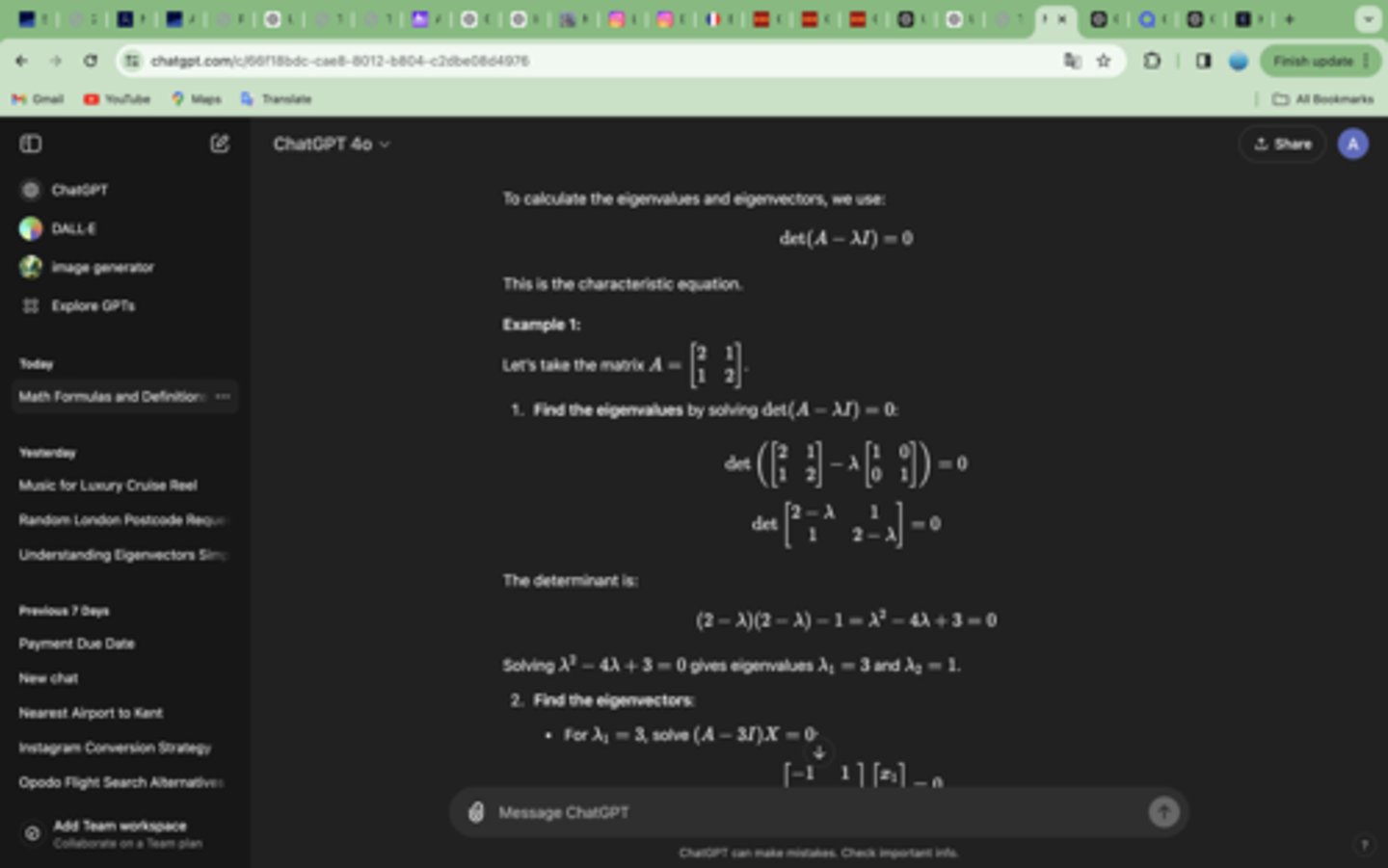
To calculate the eigenvalues and eigenvectors, we use:

det(A−λI)=0

This is the characteristic equation.

Answer to this: Find the eigenvalues by solving det(A−λI)=0

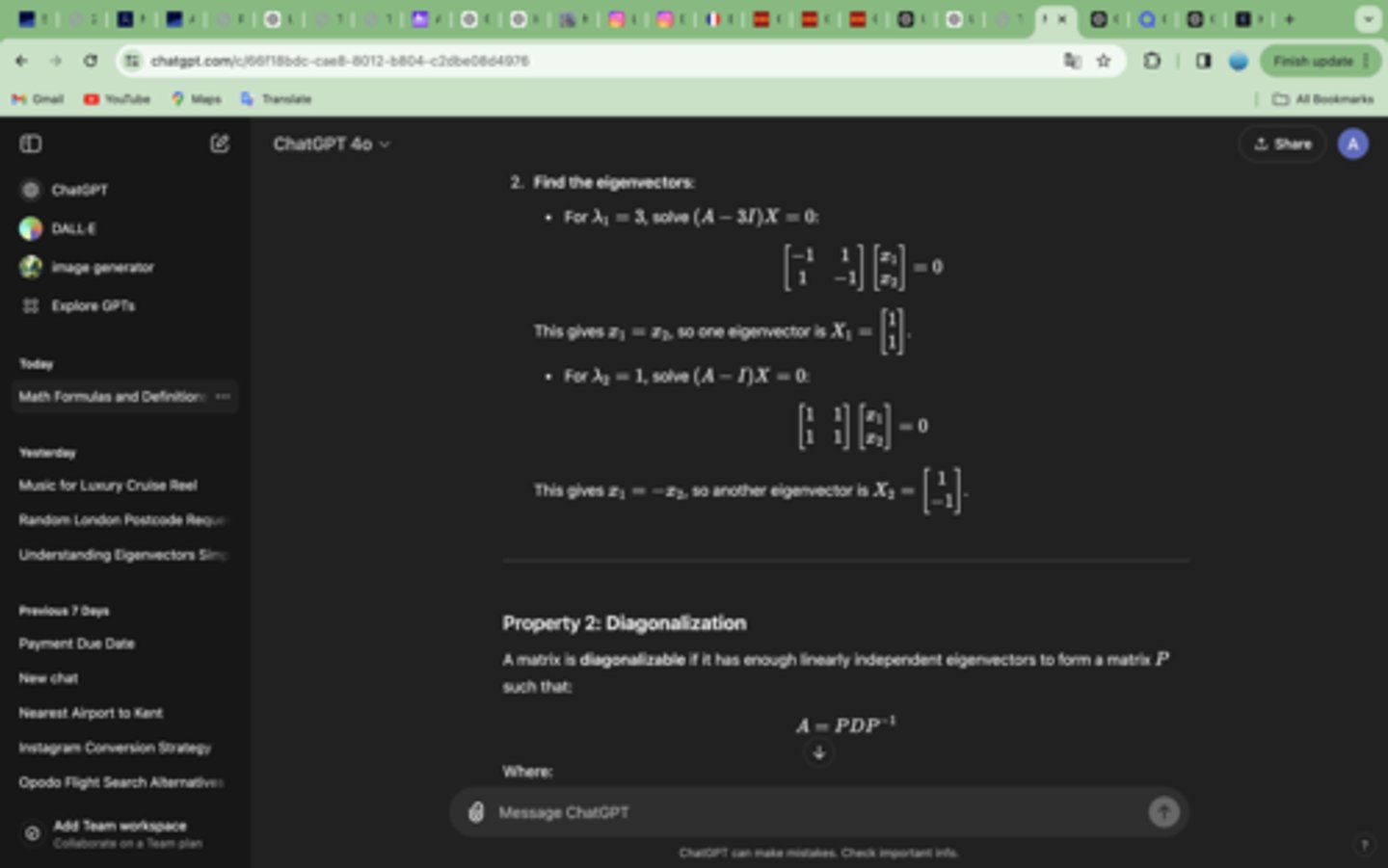
Find the eigenvectors by solving (A−λI)X=0

AX=λX and (A-λI)X is the same

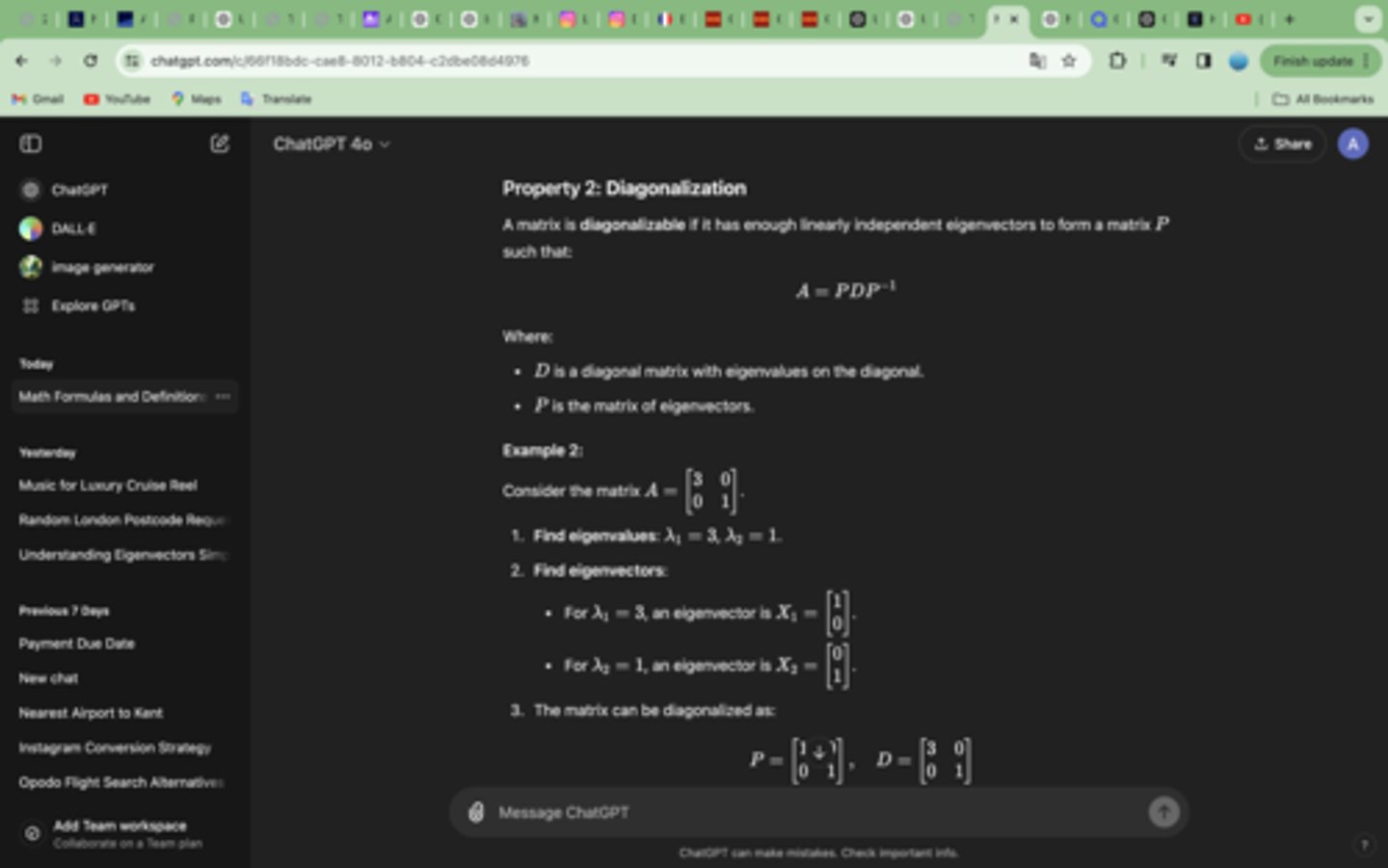
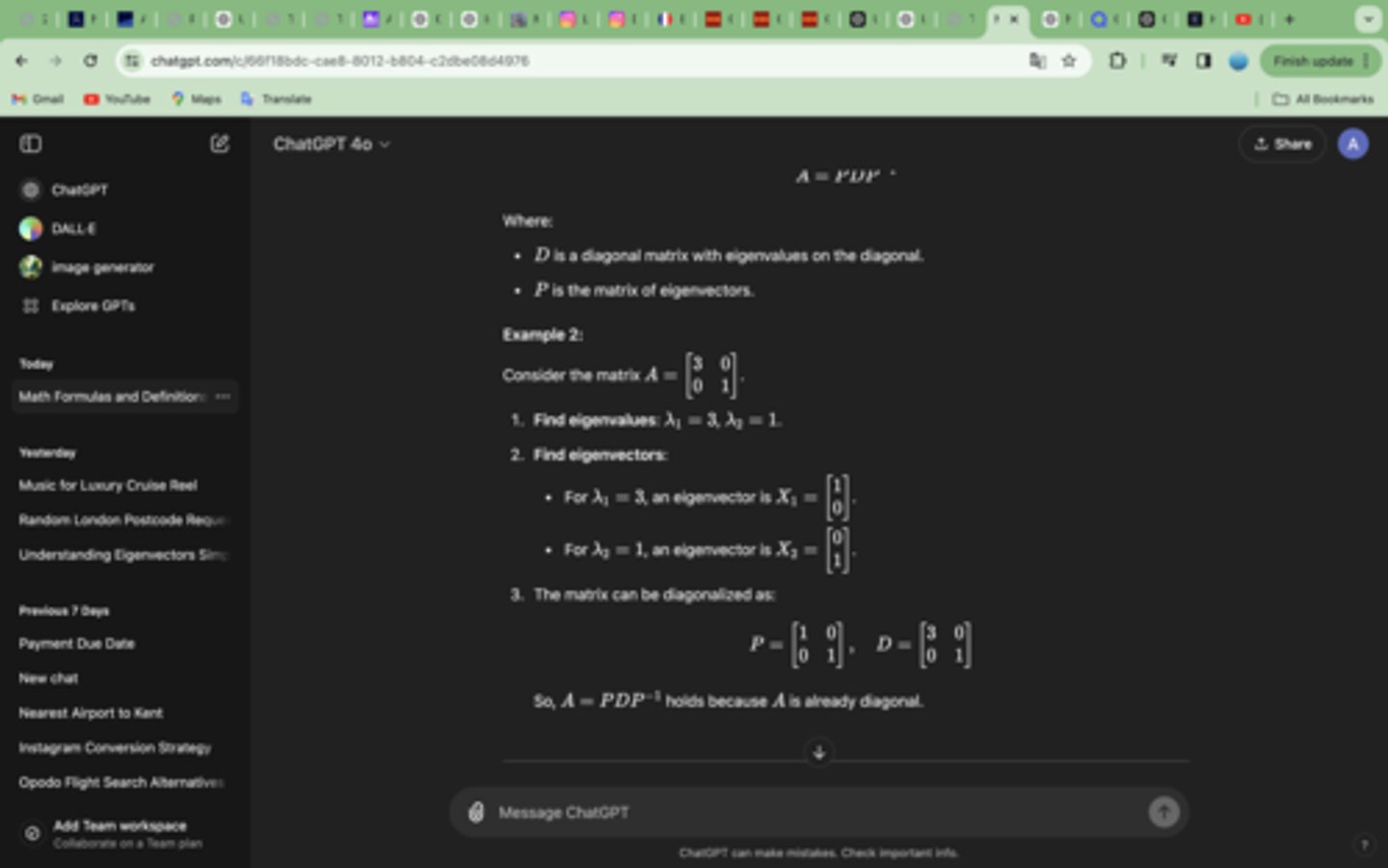
A matrix is diagonalizable if it has enough linearly independent eigenvectors to form a matrix P such that:

A=PDP^-1

How to diagonalise a matrix and make sure it's right

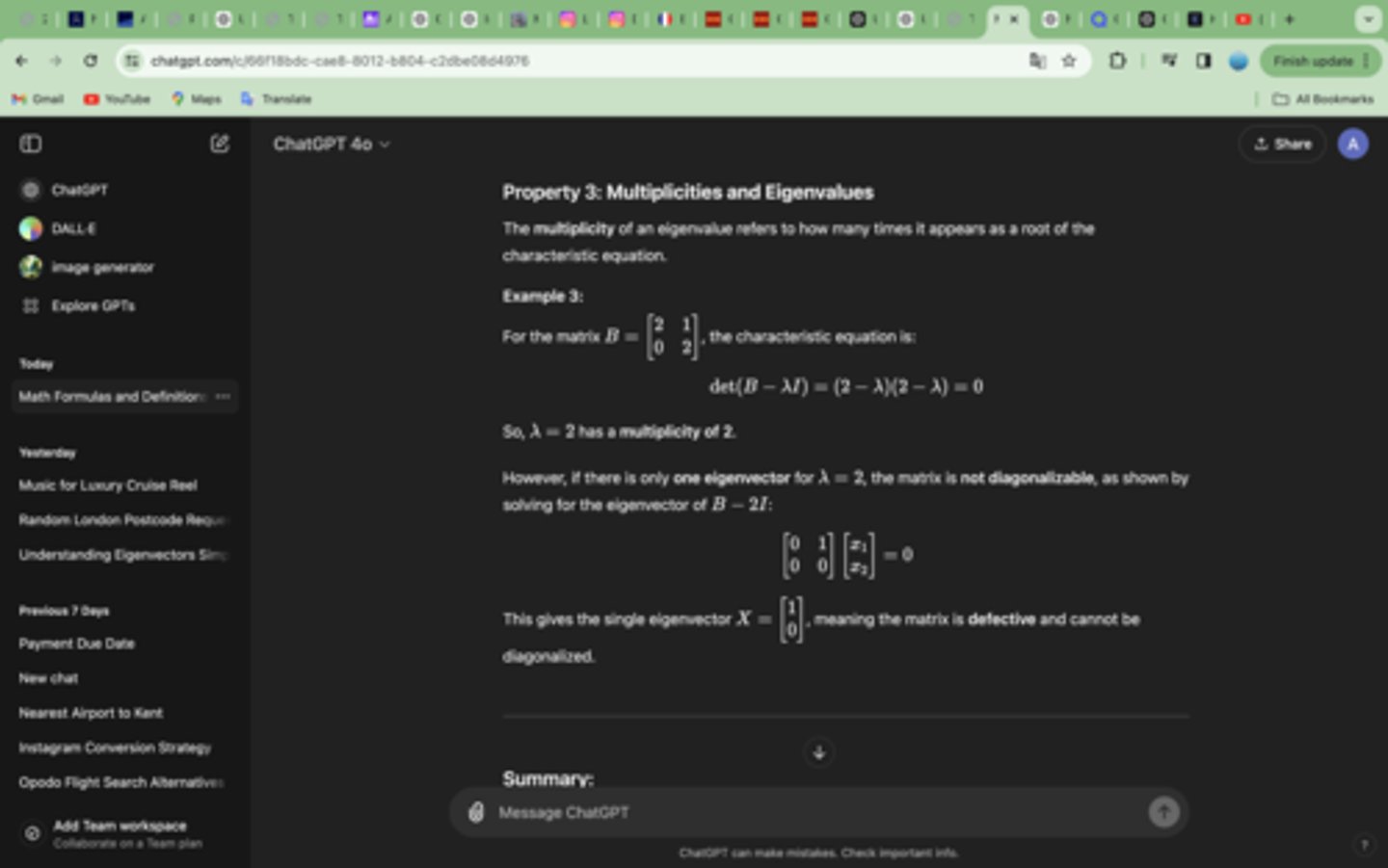
Property 3: Multiplicities and Eigenvalues

The multiplicity of an eigenvalue refers to how many times it appears as a root of the characteristic equation.