Chapter 14 - Chemistry II

Chemical Kinetics (Chapter 14)

Study of the rate (speed) at which chemical reactions occur, i.e., explosions, medications, rusting, erosion

The speed at which chemical reactions take place is called reaction rate

Reaction Rates (Chapter 14)

The speed of a chemical reaction — its reaction rate — is the change in concentration of reactants or products per unit of time (M/time)

Four factors influence rate:

• Physical state of the reactants

• Reactant concentrations

• Reaction temperature

• Presence of a catalyst

Physical State of the Reactants (Chapter 14)

Influenced by collision frequency and phase

The more readily the reactants collide, the more rapidly they react

Homogeneous reactions (all gases or liquids) are often faster

Heterogeneous reactions that involve solids are slower

Reactant Concentrations (Chapter 14)

Most reactions often proceed faster if the reactant concentration is increased

There are more molecules, so more collisions are possible

If the surface area is increased the reaction rate increases, i.e., a fine powder (thin fibers) reacts faster than a pellet or tablet

Reaction Temperature (Chapter 14)

Reaction rate generally increases with increased temperature

Kinetic energy of molecules is related to temp

At higher temperatures, molecules move more quickly, increasing numbers of collisions and the energy the molecules possess during the collisions

More molecules cross the barrier to reaction (activation energy)

Presence of a Catalyst (Chapter 14)

Catalysts affect rate without being used up in the reaction

They do not appear in the overall balanced equation

Catalysts affect the kinds of collisions. Often change the mechanism (individual reactions that are part of the pathway from reactants to products).

Catalysts are critical in many biological (enzyme) and industrial reactions

Reaction Rate (Chapter 14)

Reaction rate is a change in concentration over a time period: △ [ ] / △ t

• △ represents “change in”

• [ ] represents molar concentration

• t represents time

By convention, reaction rates are always expressed as positive quantities

Average and instantaneous rates are measured to understand a reaction

Average Rate (Chapter 14)

Rate can measure the increase in [product] with time

Rate can measure the decrease in [reactant] with time

Here balls (change from red to blue) are used to illustrate the progress of a reaction over time

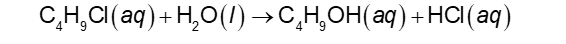
Following a Reaction Rate (Chapter 14)

In this example, [C₄H₉Cl] is measured to find the average rate

Instantaneous Rate (Chapter 14)

This figure shows rate data for [C₄H₉Cl]

The rate at time zero is called the initial rate

It is difficult to measure concentration at time zero, so a time (t) is chosen during the course of reaction to assess the reaction

The slope of the curve at one point in time gives the instantaneous rate

The rate is calculated using the slope of tangent to the line at time t

Reaction Rates and Stoichiometry (Chapter 14)

Rates mA be measured using either reactant or product

Will this give the same rate for each reactant and product?

• Answer

If we measured the disappearance of C₄H₉Cl and compared it to the appearance of C₄H₉OH, the magnitudes would be the same

The numbers would have opposite signs — one goes down (reactant), the other (product) goes up

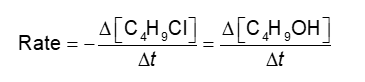
Average Rates Depend on Stoichiometry Coefficients (Chapter 14)

What if the equation is not 1:1 stoichiometry?

Use the stoichiometry coefficient as a fraction, i.e., a stoichiometric coefficient of 2 would become a ½ in setting up the rate equality

The relative rates would be:

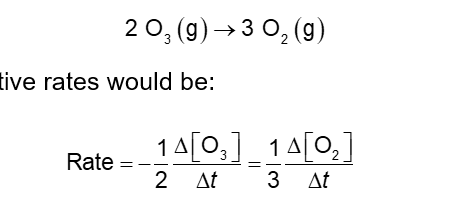
Rate Laws and Rate Constants: The Method of Initial Rates (Chapter 14)

Rate laws are mathematical statements that must be detrimental experimentally for every reaction

If A → B

• k = specific rate constant

• x, y = refer to reactant order

Reaction order:

• The order with respect to each reactant is 1. It is first order in NH₄⁺ and NO₂^-

• The reaction order is second order (1+1 = 2). Add up all of the reactants orders to get the overall reaction order.

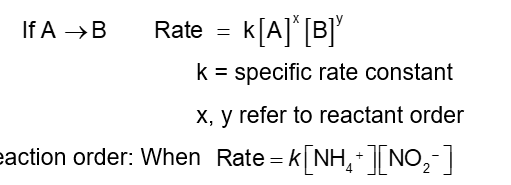
Order ≉ Stoichiometry (Chapter 14)

The order of the reaction must be determined experimentally. It is not necessarily related to the balanced equation:

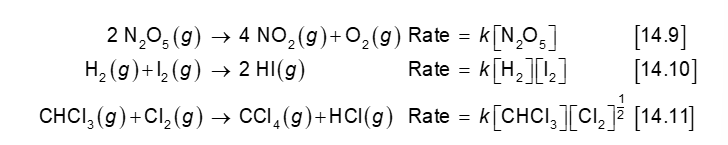
Magnitudes and Units of K (Chapter 14)

Magnitude:

• For reactions with k~10⁹ or higher, the reaction is considered fast

• For reactions with k less than 10 or lower, the reaction is considered slow

• If Rate is M/s, units of k: Zero order - Ms^-1

  • 1st order - s^-1

  • 2nd order - M^-1s^-1

Method of Initial Rates (Chapter 14)

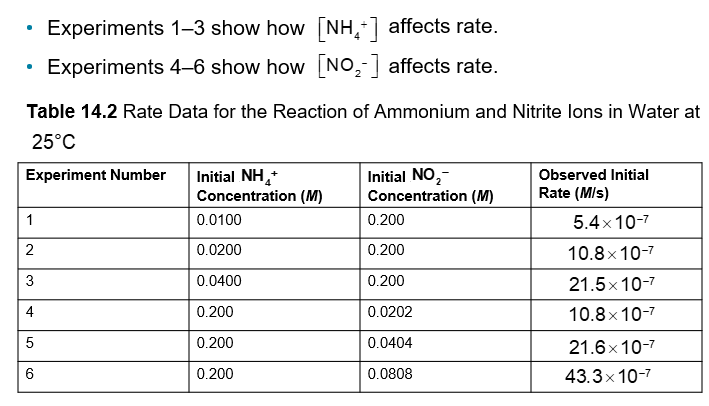
To determine the rate law, choose two experiments in the data set where one reactant is constant and the other reactant varies

Set up ratio of rates versus reactant concentration

• conc ratio^exponent = rate ratio

It is useful to place the larger rate on top

The following example has NO₂^- and NH₄⁺ as reactants

Exponents and the rate constant need to be determined for

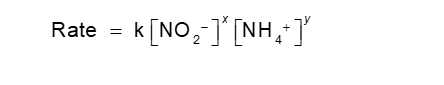
An Example of How Concentration Affects Rate (Chapter 14)

Finding y: In experiments 1-3, the NO₂^- concentration is constant, so any change in rate is due to [NH₄⁺]

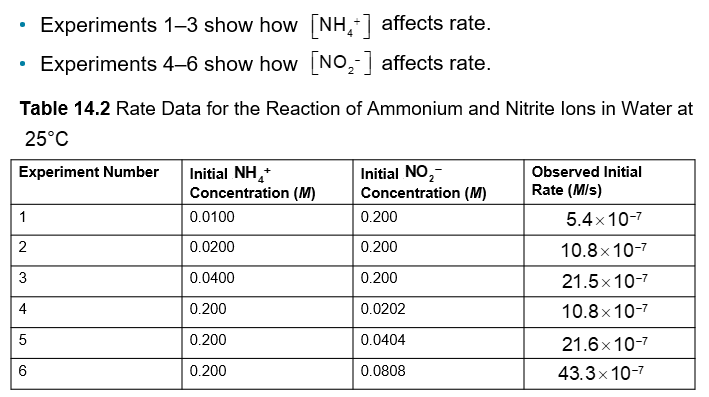
An Example of How Concentration Affects Rate Pt. 2 (Chapter 14)

Finding x: In experiments 1-3, the NH₄⁺concentration is constant, so any change in rate is due to [NO₂^-]

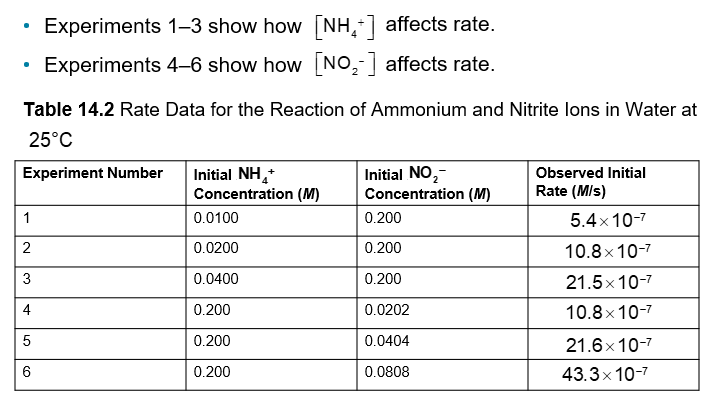
An Example of How Concentration Affects Rate Pt. 3 (Chapter 14)

Result: The rate law, which shows the relationship between rate and concentration for all reactants:

To find the value of k, substitute in the values for any of the experiments:

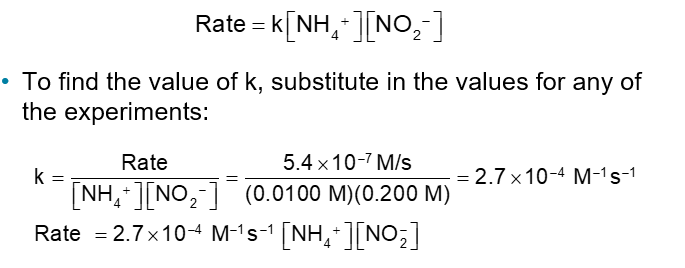
Integrated Rate Laws (Chapter 14)

The method of initial rates can often lead to error

Graphical treatment using the concentration and time data allows for a better determination of the rate law

• Focus on the integrated forms of the rate laws not how they are determined

Rate Law — equation that relates rate (M/time), rate constant (k) and concentration (M) of reactants

Integrated Rate Law — equation that relates time and concentration (M)

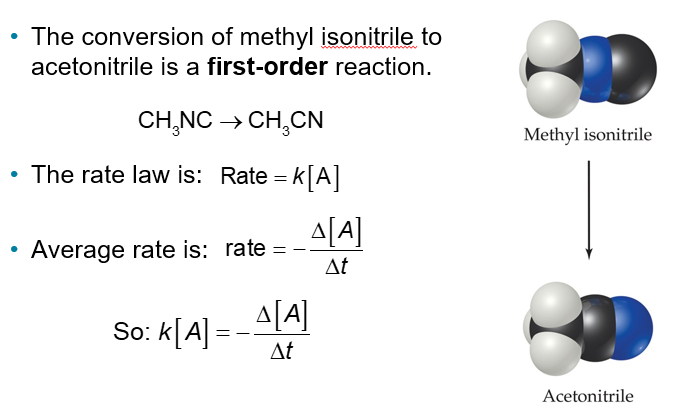
First-Order Reactions (Chapter 14)

The conversion of methyl isonitrile to acetonitrile is a first-order reaction

Finding the Rate Constant, k (Chapter 14)

Besides determining the rate law, we can find the rate constant from the plot of In[A] versus t.

Remember the integrated rate law:

This plot will give a lin. Its slope will equal -k

Second-Order Reactions (Chapter 14)

Rates that depend only on a reactant to the second power

An example of a Second-Order Reaction: Decomposition of NO₂ (Chapter 14)

A plot following NO₂ decomposition shows that it must be second order because it is linear for 1/[NO₂], not linear for In[NO₂]

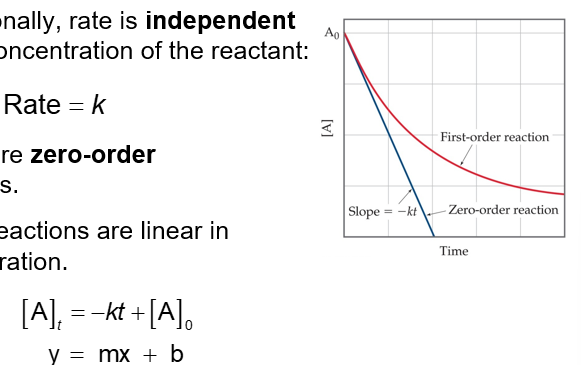
Zero-Order Reactions (Chapter 14)

Occasionally, rate is independent of the concentration of the reactant:

Rate = k

These are zero-order reactions

These reactions are linear in concentration

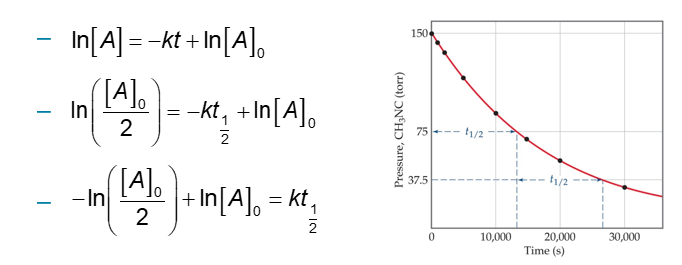
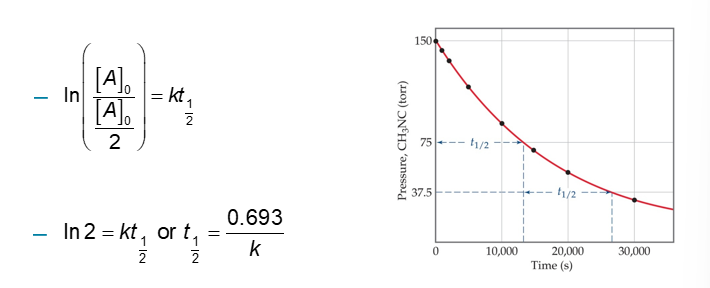
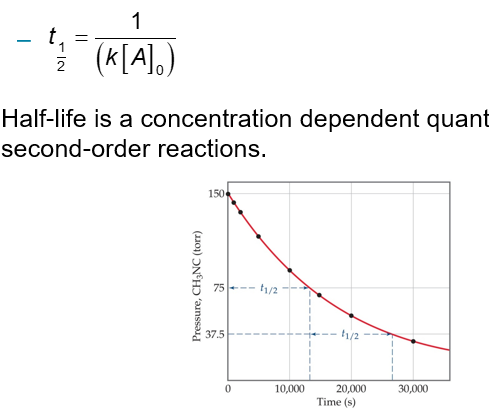
Half-Life for First-Order Reaction (Chapter 14)

Definition: The amount of time it takes for one-half of a reactant to be used up in a chemical reaction

First-Order Reaction:

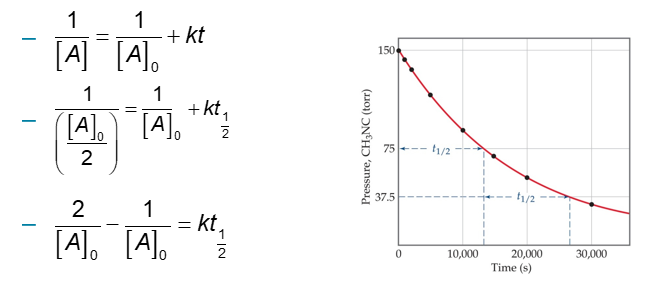
Half-Life and Second-Order Reactions (Chapter 14)

Using the integrated rate law, we can see how half-life is derived:

Half-life is a concentration dependent quantity for second-order reactions

Temperature and Rate: Activation Energy and the Arrhenius Equation (Chapter 14)

Rates of most reactions increase as temperature increases, i.e. a light stick will be brighter, dough will rise more quickly

Look at a rate law:

• Temperature cannot affect concentration, so the rate constant, k, must change with temperature

Other favors: frequency of collisions, orientation of molecules, energy needed for the reaction to take place

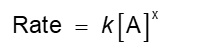
Temperature and Rate (Chapter 14)

Generally, as temperature increases, rate increases

The rate constant is temperature dependent: It increases as temperature increases

Rate constant doubles (approximately) with every 10°C rate

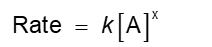
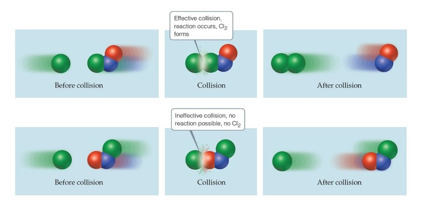
Collision Model (Chapter 14)

Based on the kinetic molecular theory.

Molecules must collide to react

• If there are more collisions, more reactions can occur

• If there are more molecules, the reaction rate is faster

In a chemical reaction, bonds are broken, and new bonds are formed

Molecules can only react if they collide with each other

Molecules must align properly

Orientation Factor (Chapter 14)

Shortcomings:

• Does not explain the minimum energy requirement

• Not direct method to calculate the probability molecules will have the correct orientation except in very simple systems

Activation Energy Model (Chapter 14)

The minimum energy needed for a reaction to take place is called activation energy

An energy barrier must be overcome for a reaction to take place, i.e. reactant to product. Much like the ball must be hit overcome the barrier in the figure below.

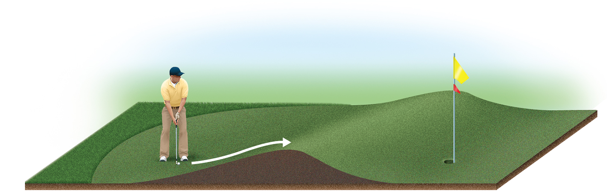
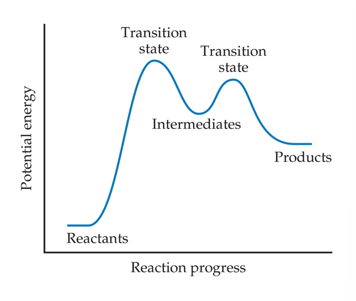
Transition State (Activated Complex) (Chapter 14)

Reactants must gain energy as the reaction proceeds until the particles reach the maximum energy state

The organization of the atoms at this highest energy state is called the transition state (or activated complex).

The energy needed to form this state is called the activation energy (E_a)

It is energy difference between energy of the reactants and the highest energy along the reaction pathway

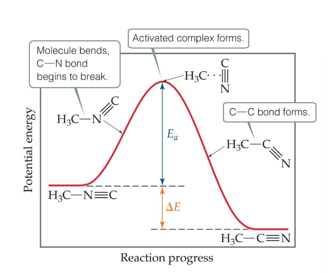
Reaction Progress (Chapter 14)

Plots are made to show the energy possessed by the particles as the reaction proceeds

At the highest energy state, the transition state is formed

Reaction can proceed to product or return to reactant

Rate constant (k) depends on the magnitude of E_a

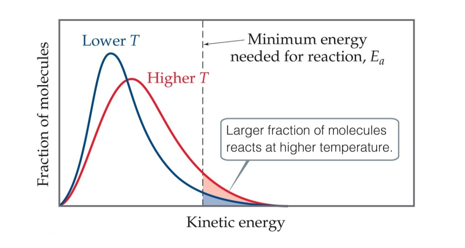
Effect of Temperature on the Distribution of the Energy of Molecules (Chapter 14)

Molecules have an average temperature, but each individual molecules has its own energy

At higher energies, more molecules possess the energy needed for the reaction to occur

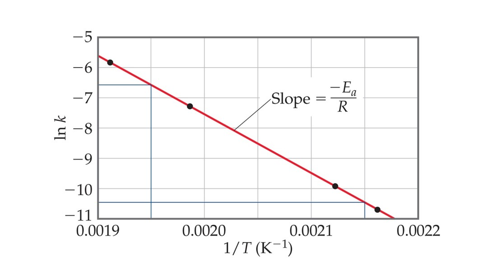
Determining Activation Energy (Chapter 14)

Arrhenius found the relationship between activation energy and temperature:

Activation energy can be determined graphically by reorganizing the equation

Plotting

One can also calculate k at a new temperature given E_a with k at a given temperature

E_a can also be determined by plotting reaction data at various temperatures

Reaction Mechanisms (Chapter 14)

Describes the steps by which reactions occur

• Reaction that occurs by a single step is known as an elementary reaction

• Reaction mA also occur thought several discrete steps

The molecularity of an elementary reaction tells how many molecules are involved in that step of the mechanism

• Unimolecular: involves a single molecule

• Bimolecular: two molecules collide

• Termolecular: three molecules collide

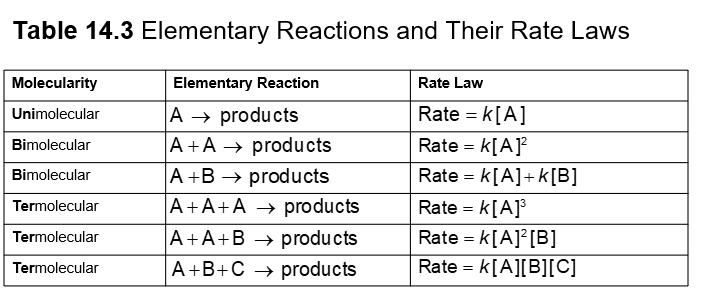
Termolecular Possibility (Chapter 14)

Termolecular steps require three molecules to simultaneously collide with the proper orientation and the proper energy

These are rare, if they indeed to occur

These must be slower than unimolecular or bimolecular steps

Nearly all mechanisms use only unimolecular or bimolecular reactions

What Limits the Rate? (Chapter 14)

The overall reaction cannot occur faster than the slowest reaction in the mechanism

We call that step the rate-determining step

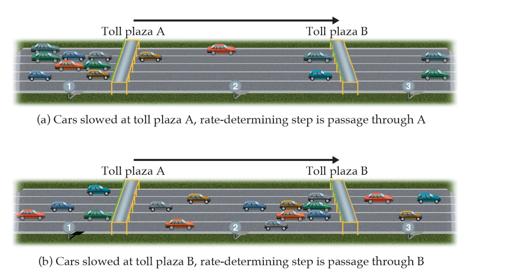
Requirements of a Plausible Mechanism (Chapter 14)

The rate law must derived from the rate-determining step

The rate determining step us the slow step

Each step must balance, like any equation

All intermediates are made and used up

The stoichiometry must be obtained when all steps are added up

Any catalyst is used and regenerated

A Mechanism with a Slow Initial Step (Chapter 14)

Overall Equation:

Rate Law:

A mechanism is proposed with the first step, the rate determining step as the slow step:

The molecules NO₃ is called an intermediate: produced in the first step, used in the second step

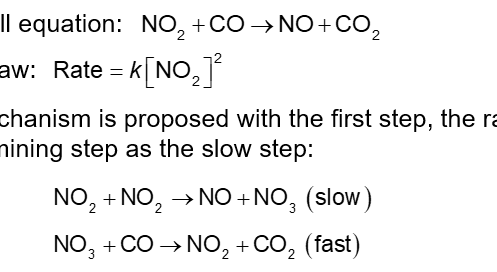
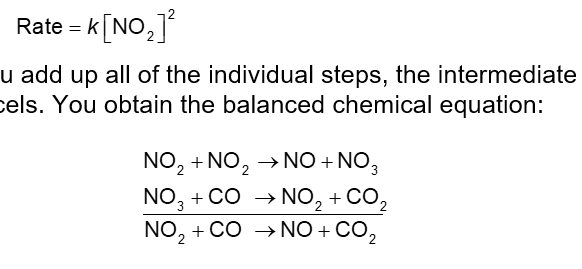
A Mechanism with a Slow Initial Step Pt. 2 (Chapter 14)

Since the first step is the slowest step, it gives the rate law.

If you add all of the individual steps, the intermediate cancels. You obtain the balanced chemical equation:

This is a plausible mechanism

Intermediates (Chapter 14)

An intermediate is not a reactant or a product

It is also not the transition state

Intermediates are stable

They occur along the reaction pathway

In some instances, it is possible to isolate or identify an intermediate

A Mechanism with a Fast Initial Step (Chapter 14)

Given the termolecular reaction:

The rate law for this reaction was found to be

The following mechanism was proposed

NOBr₂ the intermediate can react two ways:

• With NO to form NOBr

• Decomposition to reform NO and Br₂

The reactants and products of the first step are in equilibrium with each other

For an equilibrium

Rate_f = Rate_r

Subscripts f and r designate the forward and reverse, respectively

Catalysis (Chapter 14)

A catalyst is a substance that changes the speed of a chemical reaction without undergoing a permanent chemical change itself

A catalyzed reaction (blue curve) is faster than an uncatalyzed reaction (red curve)

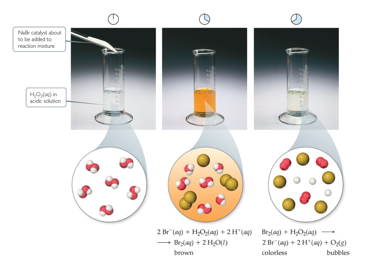
Homogeneous Catalysts (Chapter 14)

The reactants and catalyst are in the same phase

Many times, reactants and catalyst are dissolved in the same solvent, as seen below

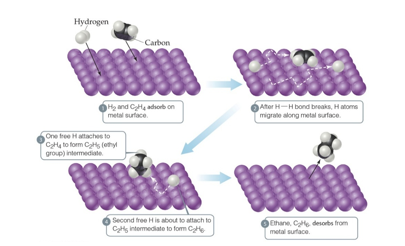
Heterogeneous Catalysts (Chapter 14)

The catalyst is in a different phase than the reactants

Often, gases are passed over a solid catalyst

The adsorption of the reactants is often the rate-determining step

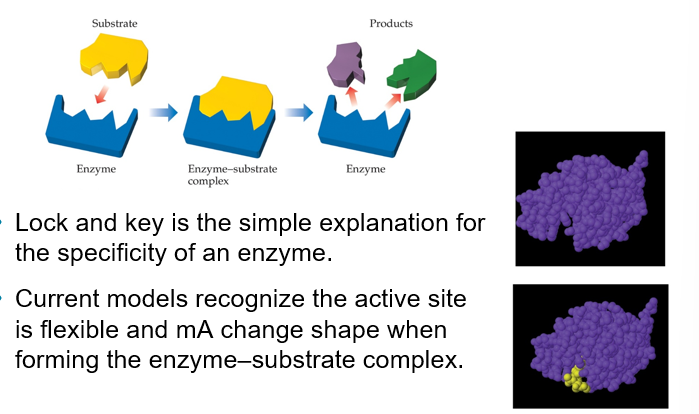
Enzymes (Chapter 14)

Are biological catalysts

The reaction that any specific enzyme reaction take place at a specific location in the enzyme is called the active site

The substances that react at this site are called substrates

Lock-and-Key Model (Chapter 14)

Lock and key is the simple explanation for the specificity of an enzyme

Current models recognize the active site is flexible and mA change shape when forming the enzyme-substrate complex