Topic 4: Risk, Return and Minimum-Variance Portfolios

Why is investment important?

• Helps future accountants and finance professionals advise business and clients on optimal investment strategies.

• It builds the ability to assess, quantify, and mitigate financial risks

Define a Stock, Bond and Corporation

• Stock – a security that gives some ownership (also called equity)

• Bond – a security that represents a loan or debt

• Corporation – a type of company with many owners (stockholders)

Suppose you sell 1,000 shares to an investor for £10,000 and you keep 1,000 shares (to pay for your time)

Suppose you borrow £5,000 from a bank (sell them a bond) for a one year at 10% interest: total investment: £25,000.

If you make £29,500 and close the company, what would you do with the money?

• Pay £5,500 to the bank → principal + interest

• pay £12,000 to your investor

• Pay £12,000 to yourself-

What percentage return did the investment earn?

• 12000-10000/10000 = 20 %

• Return is just percentage change in value – can be positive or negative

• Security values are what you can sell them for

What return did the bank earn?

• You and your investor earned 20%, while the bank only got 10%.

Suppose you decide to grow your company instead of closing it after 1 year.

You have great success – everyone wants to be an egg producer.

You decide you will need 5 stores, 7 new chicken coops, and 50 employees

What will you do?

• can find new stockholders

• Have an initial public offering (IPO)

• Get listed an a stock exchange NYSE or Nasdaq (in the US) LSE (in the UK)

• Get a ticker symbol (maybe Hei?)

• Track your company value every day

• Use the money you get to grow the business

Who decides what your stock is worth?

• people buying/selling your stock (links to S/D)

What makes your stock’s value change from day to day?

• Lots of types of news affect the value of your company from day to day

• Firm-specific news, like how much money you make, can drive your stock price up or down

• Market news, like how the entire economy is doing, can also move prices

• Prices on any given day move up or down together

• Returns across stocks are correlated with each other

To keep track of how the stock market is doing, what do people calculate?

• indices/averages of returns

What is a return?

• Let’s say you paid Pt in date t for an asset

• In date t + 1 the price P is Pt+1

• Then, the return is:

• simply a normalisation of the “pound gain” by the cost of the asset

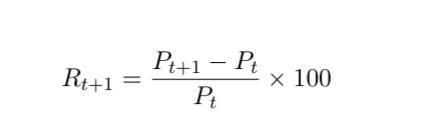
How Returns are Distributed?

• The distribution of returns describes how investment returns are spread out or arranged across different values

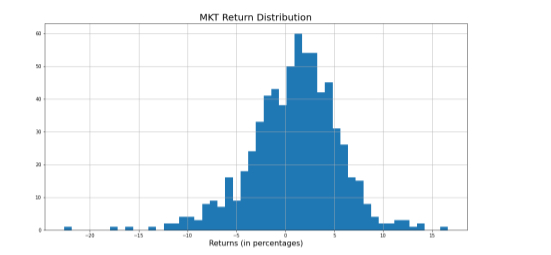
identify three features that are noteworthy about this plot

• It is centered around the 0% and 2%.

• It has a shape, and most extreme observations are on the side of the plot

Can we measure the features of the plot?

• calculate the sample moments of the distribution of returns for the “market” portfolio.

Define Moments in statistics

• ways to describe the shape and features of a data

  distribution.

Calculate the mean of the return distribution

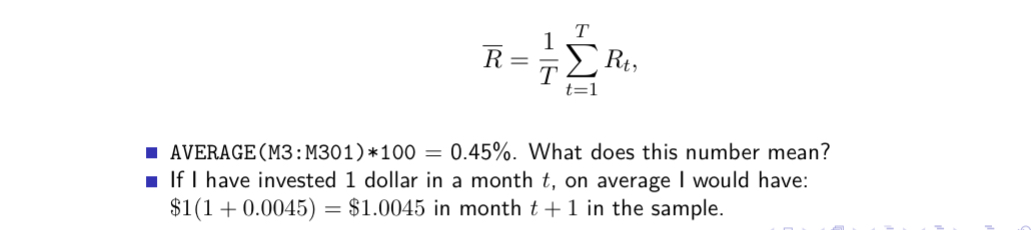
Calculate the SD of the return distribution

• STDEV.S(M3:M301)*100 = 6.32%. What does this number mean?

• If I invest all my wealth, say $100K in the market in month t, then the standard deviation of my wealth in date t is 4.51% in the sample.

• In a normal distribution, about 68% of outcomes would fall within one standard deviation of the mean.

• The expected value in t + 1 would be about $100,910.

• About 68% of the time, your ending wealth would fall between $96,400 and $105,420,

  i.e., –3.6% and 5.42%.

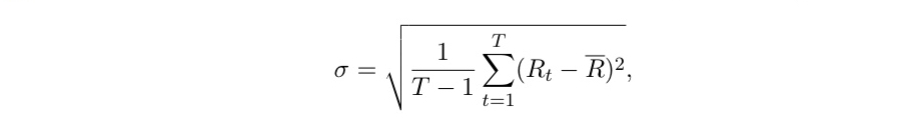
What does skewness tell us about a return distribution?

Skewness measures asymmetry in returns:

• SK = 0: symmetric distribution

• SK > 0: longer right tail (higher chance of extreme gains)

• SK < 0: longer left tail (higher chance of extreme losses)

A dataset of returns has skewness of −0.61. What does this indicate?

• distribution has a longer left tail, meaning there is a higher probability of extreme losses.

What does kurtosis tell us about a return distribution?

Kurtosis measures tail thickness:

• KU = 0: normal tails

• KU > 0: fat tails (more frequent extreme outcomes)

• KU < 0: thin tails (less frequent extreme outcomes)

A dataset of returns has excess kurtosis of 2.57. What does this indicate?

• The distribution has fat tails, meaning extreme returns (crashes or booms) are more likely than under a normal distribution.

How can skewness and kurtosis together describe how returns are distributed?

• Skewness shows the direction of asymmetry (risk of extreme gains vs. losses), while kurtosis shows the likelihood of extreme returns.

• Together, they reveal that returns are not perfectly normal and can have higher risk of extreme events.

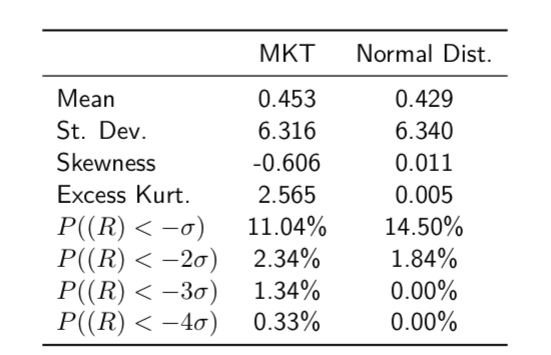
Look at the data, what does the normal distribution show?

• decent approximation for market returns;

  however, it fails to replicate the extreme events we observe empirically.

What are the two main sources of risk for a company?

• Firm-specific risk, also known as idiosyncratic risk, refers to the risk unique to a specific company.

• Market-risk, also known as systematic risk, refers to the risk that affects the entire market or a broad segment of it.

Can you eliminate risk?

• Only idiosyncratic risk through diversification.

Define diversification

• combining assets in a portfolio to reduce total risk without sacrificing too much portfolio return

Definition of a portfolio

• collection of assets, characterised by the mean,

  variances/covariances of their returns

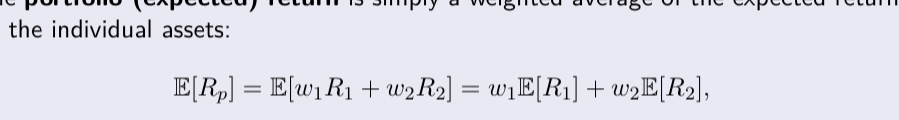
Definition of portfolio (expected) return

• weighted average of the expected returns on the individual assets:

• w1 and w2 are weights following the following properties:

• 0 ≤ w1 ≤ 1 and 0 ≤ w2 ≤ 1

• w1 + w2 = 1

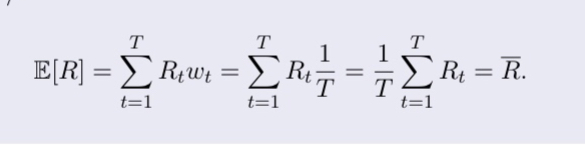
Define expectation operator

• generalisation of the weighted average.

• assuming weights as wt = 1/T:

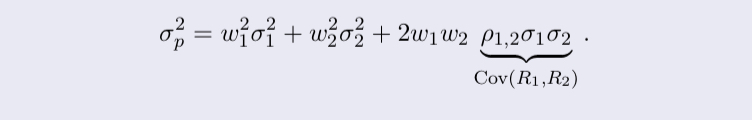
Define variance of a portfolio

• weighted average of variances and covariances

variance of an asset is computed as:

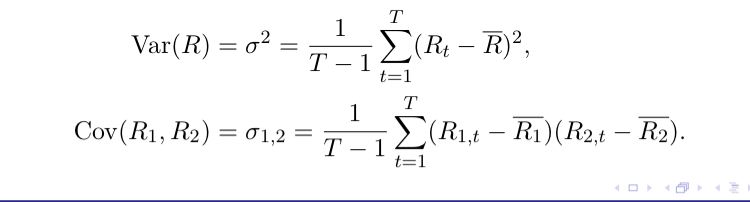
standard deviation of the portfolio is:

• σ2/1 and σ2/2 are respectively the variance of assets 1 and 2.

• w1 and w2 are weights.

• ρ1,2 denotes the correlation coefficient.

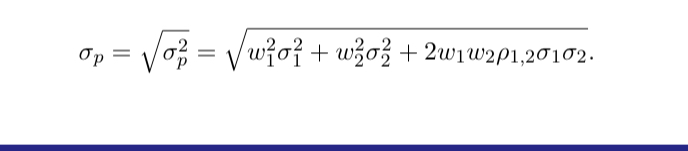
correlation

• tells us whether two variables tend to move together, in opposite directions or independently.

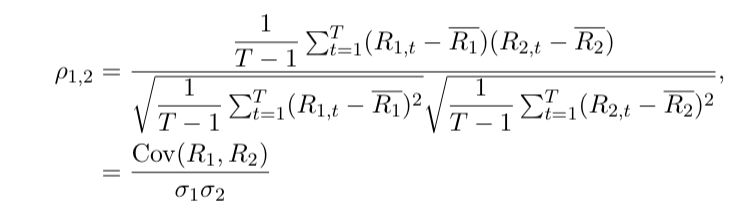
correlation coefficient is estimated as:

• Covariance is positive (negative) when bad and good outcomes for each asset tend to occur together (at dissimilar times).

• Correlation is a measure of standardised covariance ranging from −1 to 1.

The concept of risk in a portfolio, relates to what?

• return from a portfolio is not constant over time

What happens to portfolio risk and return when two assets are perfectly positively correlated (ρ = +1)?

• Portfolio return is the weighted average: Rp =w1 R1 +w2 R2

• Portfolio risk is also the weighted average: σp =w1 σ1 +w2 σ2

• No diversification benefit: investing in both assets does not reduce risk.

How do combinations of two perfectly positively correlated assets appear in risk-return space?

• portfolio combinations lie on a straight line between the two assets, reflecting linear weighting of risk and return.

Q: Why doesn’t perfect positive correlation reduce portfolio risk?

• the assets move exactly together, so combining them doesn’t cancel out any fluctuations

• risk is just the weighted average of individual risks.

How does perfect negative correlation affect portfolio risk?

• Rp=w1R1+w2R2

• There exists a combination with zero risk:w1 =σ2 /(σ1 +σ2 )

• All portfolio combinations lie on two straight lines in risk-return space

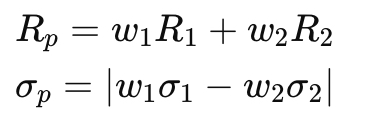
What happens to portfolio risk and return when two assets are uncorrelated?

• Portfolio combinations lie on a curved line between the straight-line extremes of ρ = +1 and ρ = −1

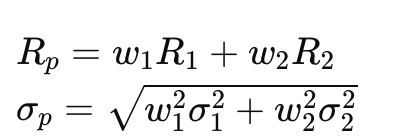
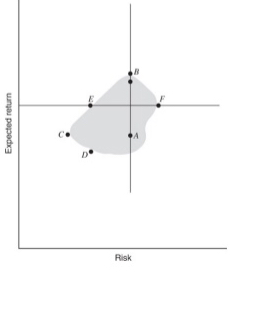
plot depicts all possible portfolios or assets in the risk-return space

• B and A have the same risk, but A has higher

return. C and A have the same return, but C has

lower risk.

• D and E have the same risk, but E has higher

return.

• Therefore, C is called the global minimum

variance portfolio, and B is the maximum return

portfolio.

plot depicts all possible portfolios or assets in the risk-return spac

• B and A have the same risk, but A has higher

  return. C and A have the same return, but C has

  lower risk.

D and E have the same risk, but E has higher

return.

• Therefore, C is called the global minimum

variance portfolio, and B is the maximum return

portfolio.

• efficient frontier consists of the curve that is

formed between the global minimum variance and

the maximum return portfolio.

When correlation between assets is ρ1,2 < +1, the efficient frontier forms from all possible combinations of those assets. Meaning?

• Lower correlation: stronger diversification benefit

• Imperfect correlation allows reduced risk without sacrificing expected return.

How are the return and variance of a portfolio composed of two risky assets calculated?

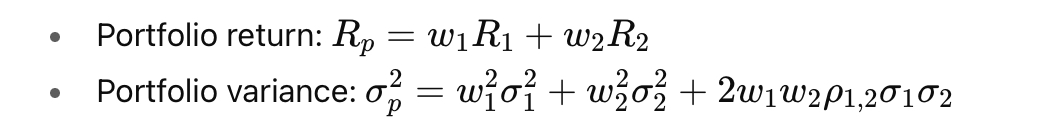
What is the objective when constructing a minimum-variance portfolio?

• To find the weights w1 and w 2  that minimize portfolio variance, subject to w1+w2=1

How can the portfolio variance formula be simplified using w2= 1 - w1?

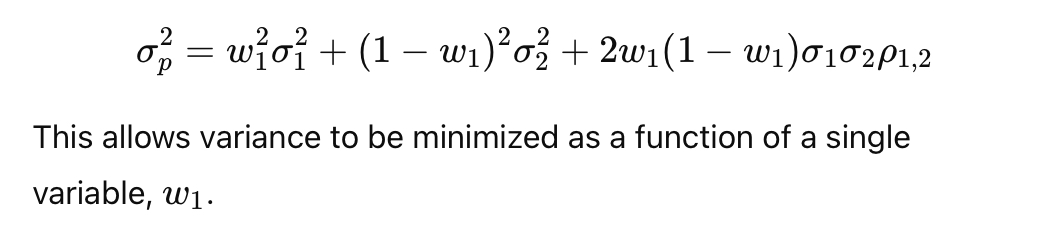
What are the weights for a minimum-variance portfolio of two risky assets?

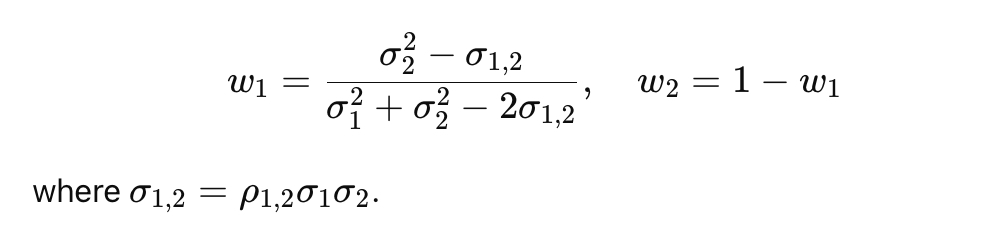
Why is the minimum-variance portfolio important in diversification?

• identifies the exact combination of assets that minimizes risk, showing the benefit of diversification even with risky assets

ETF definition

• investment fund traded on stock exchanges, much like stocks.

• ETFs typically aim to track the performance of a specific index, sector, or asset class.

What is SPY ETF?

• ETF that aims to track the performance of the S&P 500 index.

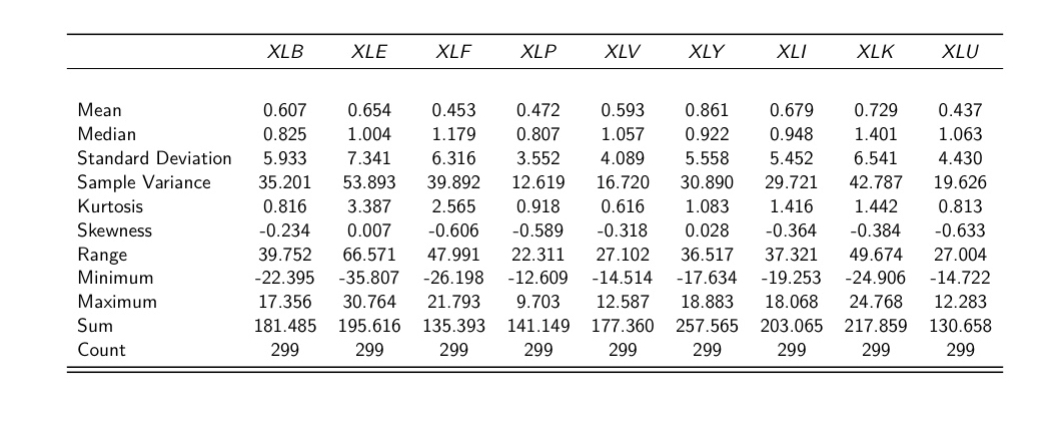
• The assets with the highest return are: XLY, XLK, and XLE.

• The most volatile assets are: XLE, XLK, and XLF.

• All assets have excess kurtosis greater than 0, and most exhibit negative skewness.

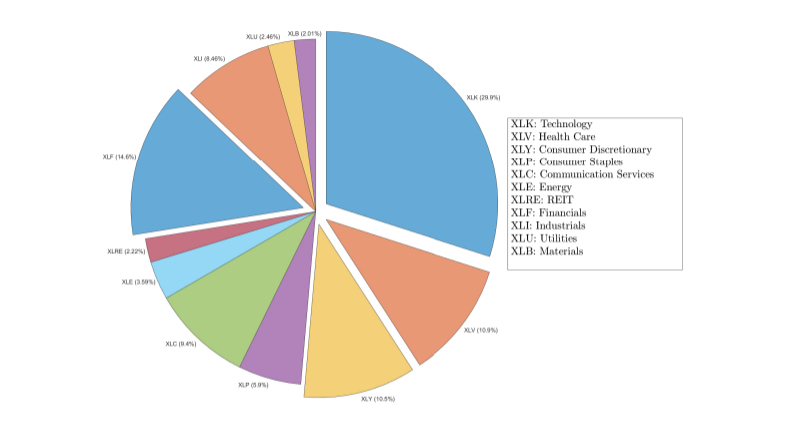
What does this show?

• XLF and XLK

  From the Pie chart, we know that XLF and XLK comprise roughly 45% of SPY.

  Both assets are more volatile than SPY, although only XLK offers a higher return than SPY.

  Their correlation is 55%, is moderately high.

• XLV and XLY

  XLV and XLY comprise roughly 22% of SPY.

  Both assets offer a higher return than SPY, and XLV is less volatile than the index

  (SPY).

  However, their correlation is 65%, which is moderate-to-high.

• XLK and XLU

  These assets show the lowest level of correlation (28%)

  They comprise roughly 32% of SPY.

  XLU is as risky as SPY, but offers a lower return, while XLK is riskier than SPY but offers a higher return.

Minimum-variance portfolios reduce

• risk compared to equally weighted portfolios.

• Risk reduction is more pronounced than return reduction.