1.3. Transport and Kinematics

Key concepts of transport phenomena

• Equilibrium state corresponds to…

• Adjacent particles with non-uniform quantities tend to…

• The return to equilibrium is due to…

• Molecular interactions transport…

• From the macroscopic POV…

Equilibrium state corresponds to… (key concepts of transport phenomena)

a uniform distribution within a volume of fluid of its physical quantities

Adjacent particles with non-uniform quantities… (key concepts of transport phenomena)

tend to equilibrium when placed in contact

The return to equilibrium is due to… (key concepts of transport phenomena)

local molecular interactions in a way that depend on the molecular structure of the medium

Molecular interactions… (key concepts of transport phenomena)

transport physical quantities across the boundaries

From the macroscopic POV… (key concepts of transport phenomena)

the non-uniform distribution of a generic quantity C between one fluid particle and the next one can be seen as a continuous variation.

So, a general law for the flux can be derived.

Transport is a ___ process

statistical

Irreversibility is …

macroscopic

The physical quantities that can be exchanged:

1. Mass

2. Heat → related to kinetic energy of molecules → temperature

3. Momentum

Quantities driving the transport

1. Fraction of molecules of a given species (concentration)

2. Kinetic energy (temperature)

3. Momentum (velocity)

What is the general expression for the flux?

the total rate of transfer of a given quantity

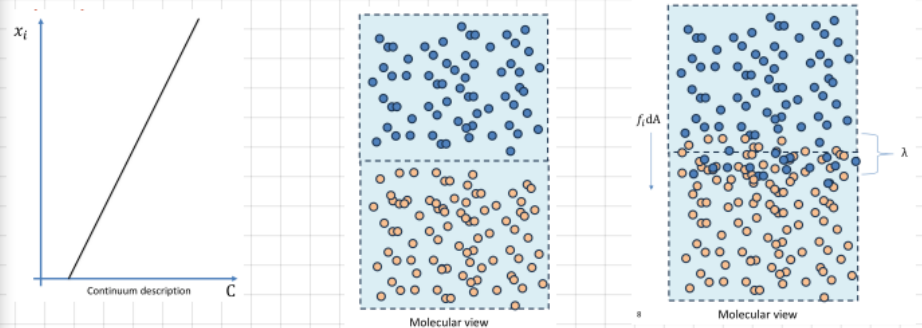
Write the general expression of the flux (total rate of transfer of a given quantity):

fi=-kij*(dC/dxj)

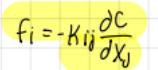
If the system is isotropic…

the general expression for the flux becomes: fi=-kappa*(dC/dxi)

kappa being the transpor coefficent → depends on the medium’s molecular properties

What is C and what are its units? (transport of mass)

C: species concentration (%)

Transport of mass from conservation laws, formula?

(dC/dt)=-(kappa_D/N)*grad²C=-K_D*grad²C

N is the total number of molecules per unit volume

K_D is the diffusivity coefficent (length² * time^-1)

Transport of mass for an ideal gas, formula?

K_d prop to lambda (u²)^1/2

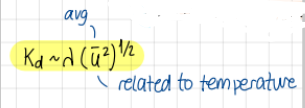
What is C and what are its units? (transport of heat)

C: temperature (K)

In transport of heat, what does f_i equate to? (2 formulas)

f_i=q_i (Heat flux(J/(sm²)))

f_i=kappa_n*(dT/dxi) (kappa_n being therman conductivity)

Transport of heat from conservation laws, formula?

(dT/dt)=-(kappa_h/(C_P*rho))*grad²*T=-K_H*grad²*T

Cp is the specific heat (heat capacity at P cte)

K_H is the thermal diffusivity (length² * time^-1)

Transport of heat for an ideal gas, formula?

K_H prop to lamda*(U²)^1/2

Definition of viscosity

Viscosity is the resistance of a fluid to flow (deformation rate) due to internal friction

Hypothesis of transport of momentum, viscosity

Simple shear flow (velocity and velocity gradient in one direction)

What is C and what are its units? (transport of momentum)

u (m/s)

In transport of momentum, what does f_i equate to?

f_i=tau_i (N/m²) → net transfer of i-components of momentum per unit time and unit area (flux)

In transport of momentum, what does tau_i equate to?

tau_i=mu*(du/dxi)

mu is dynamic viscosity (kg/(ms) or Pa*s)

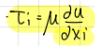
Transport of momentum from conservation laws, formula?

(Du/Dt) prop to (mu/rho)*grad²*U

where upsilon=mu/rho is the dynamic viscosity

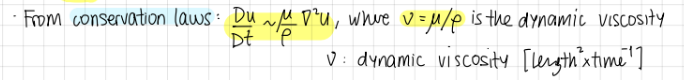
Transport of momentum for an ideal gas, formula?

upsilon prop to lambda*(U²)^1/2

Southerland’s law (transport of momentum)

mu(T)=(mu/mu0)*sqrt(T) for gases

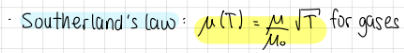
Viscosity facts

• What is viscosity coefficent or dynamic viscosity?

• What does kinematic viscosity (the ratio between viscosity and density) represent?

• Viscosity varies with ___, variation is different for …

• What is the Prandtl’s number?

What is kinematic viscosity?

The ratio between viscosity and density

What is viscosity coefficent or dynamic viscosity?

is the resistance of a fluid to flow (deformation rate)

What does kinematic viscosity (the ratio between viscosity and density) represent?

it represents the momentum diffusivity concept

Viscosity varies with ___, variation is different for …

Temperature; air (increases with temperature) and water (decreases)

What is the Prandtl’s number?

is the ratio between momentum and thermal diffusivity concept

Prandtl’s number formula

Pr=upsilon/K_H=(C_p*mu)/(kappa_H)

constant in gases

around 0.7 for air

Forces acting on a fluid particle

• Body forces

• Surface forces

Body forces characteristics

• Typically due to external fields (conservatives or not)

• Proportional to particle volume

• ex: gravity, electromagnetic, …

• a non-local force, comes externally

Surface forces characteristics

• Due to local (molecular) interactions

• Proportional to body surface

• Both normal (pressure) and tangential actions

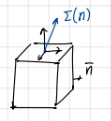
Gauss’s theorem: for a ___ domain, the following relation can be demonstrated to hold:

grad*a=divergence

if grad*a=0 → everything that goes in, goes out

Material (or Lagrangian) derivative (formula)

formula

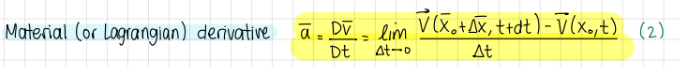
Eulerian derivative (formula)

formula

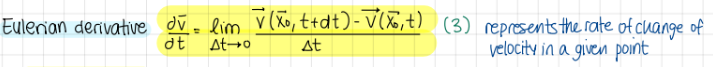
Total derivative 2 (formula)

formula

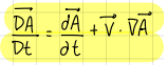
if d/dt=0

the aerodynamic system is steady/stationary

stationarity also depends on…

the reference frame

The total derivative is obtained from…

the sum of the variation in time of the considered variable plus the variation to the spatial gradients

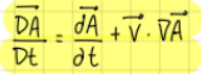
The total derivative is gotten from…

a mathematical connection between the material and eulerian derivatives

what are A and v? (total derivative)

A: vector field (or scalar fluid)

v: velocity vector

What is vorticity?

the curl of the velocity vector

Vorticity formula:

formula

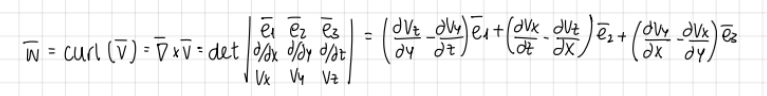
regarding vorticity, in 2D:

d/dz=0 → Vz=0

how many components of vorticity?

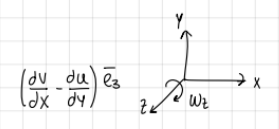
formula and graph

deformation of a fluid particle: draw diagram and write equations

diagram and equations

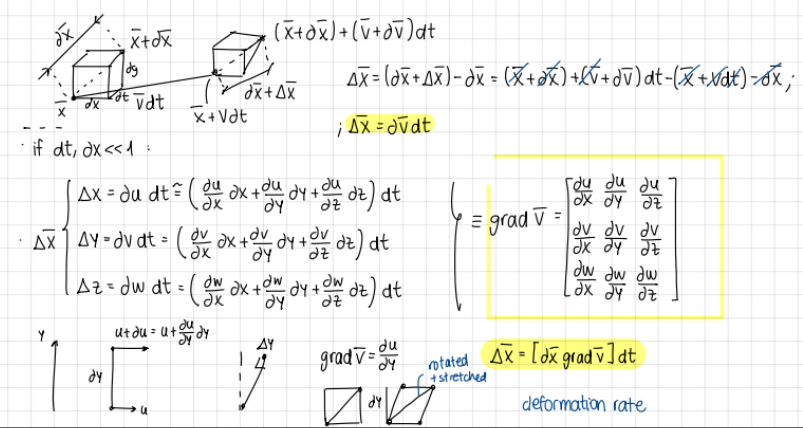
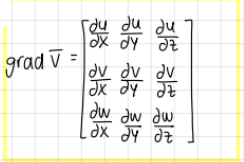
write the tensor of the gradient of the velocity vector (deformation of a fluid particle)

tensor

deltaX equal to (deformation of a fluid particle)

formula

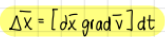
a tensor is symmetric if…

A=A^T

a_ij=a_ji

A_sym=1/2*(A+A^T)

a tensor is antisymmetric if…

b_ij= -b_ji

A_antisym=1/2*(A-A^T)

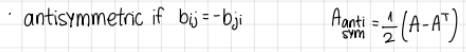
gradient of velocity vector is equal to… (formula)

gradV=E+omega

E symmetric

omega antisymmetric

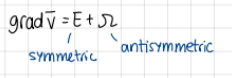
tensor of E

tensor

tensor of omega

tensor

what does deltax equal to when total deformation?

deltax= (dx*gradv)*dt

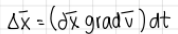
Formula for rotation rate of a particle around a given point?

formulas

omega= twice the rotation rate of a particle around a given point

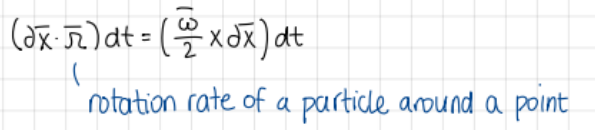
Development of rotation rate and vorticity (formulas and diagrams)

What are streamlines?

streamlines are the lines tangent to the velocity field

formulas and diagram of streamlines

what are pathlines?

pathlines are the trajectory followed by a particle

formula and diagram of pathlines

What are streaklines/smokelines?

they are the locus at a given time t of the position of the particles that at t=0 have passed by x0

how do pathlines, streamlines and streaklines relate if the flow is stationary?

pathline=streamline=streakline

What is a stream tube?

is the identified region where streamlines don’t get out and the mass flow does not go through the surface (constant mass flow)

Vortex lines/tubes characteristics

• They’re tangent to the vorticity vector

• Vortex lines are material lines (inviscid flow)