Systems of Linear Equations

linear equation

an equation that can be written in the form of

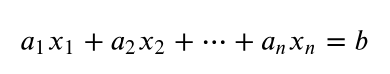
system of linear equations (linear system)

a collection of one or more linear equations involving the same variables (x₁….x_n)

ex:

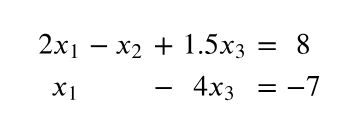
solution of the system

a list of numbers that makes each equation a true statement when the values are substitued for x₁….x_n

two linear systems are called ? if they have the same solution set

equivalent

a system of linear equations has

1. no solution

2. exactly one solution

   1. infinitely many solutions

linear equations is said to be ? if it has either one solution or indefinitely many solution

consistent

(inconsistent if it has no solution)

matrix

a rectangular array that records the essential information of a linear system,

coefficient matrix

has the coefficients of each variable aligned in columns

augmented matrix

consists of the coefficient matrix with an added column containing the constants from the respective right sides of the equations

triangular form in matrices

a pattern of zeros in a matrix forming a triangle in the lower left or upper right corner

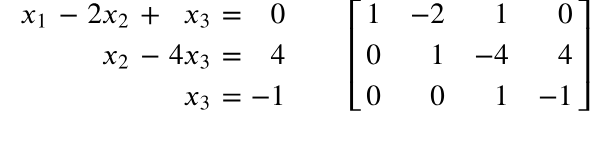
elementary row operations definition

change the form of equations, but preserves the solution

elementary row operations steps

1. replacement: replace one row by the sum of itself and a multiple of another row

2. interchange: interchange two rows

3. scaling: multiply all entries in a row by a nonzero constant

two matrices are called __ ___ if there is a sequence of elementary row operations that transforms one matrix into the other

row equivalent

if augmented matrices of two linear systems are row equivalent, then the two systems have the

same solution set

if you are lacking info to determine the values of x₁, x₂, ….,x_n (ex: 3 variables but only 2 equations), then there are

infinitely many solutions

if any matrix reduces to have a row like this: (0 0 0 … | C) and C is a non-zero constant, then it is ?

inconsistent

leading entry

refers to the leftmost nonzero entry (in a nonzero row)

a matrix is in echelon form if it follows these three properties

1. all nonzero rows are above any rows of all zeros

2. each leading entry of a row is in a column to the right of the leading entry of the row above it

3. all entries in a column below a leading entry are zeros

a matrix is in reduced echelon form if it follows these properties:

4. the leading entry in each nonzero row is 1

5. each leading 1 is the only nonzero entry in its column

a matrix can be row reduced which is the process of

transforming it into a reduced echelon form through elementary row operations

each matrix is row equivalent to ? reduced echelon matrix

(only) one

pivot positions

a location in a matrix that corresponds to a leading 1 in the reduced echelon form of the matrix

pivot column

a column of a matrix that contains a pivot position

pivot

a nonzero number in a pivot position that is used as needed to create zeros via row operations

forward phase of row reduction

the first part of the row reduction algorithm that reduces a matrix to echelon form

basic variable

a variable in a linear system that corresponds to a pivot column in the coefficient matrix

free variable

any variable in a linear system that is not a basic variable (no leading variable in that column)

solution is not unique if there are ? variables, therefore the system has infinitely many solutions

free

A linear system is ? if and only if the rightmost column of the augmented matrix is not a pivot column—that is, if and only if an echelon form of the augmented matrix has no row of the form

      [0 ⋯ 0 b]   with b nonzero

consistent

if a linear system is consistent

then the solutions set contains either

i. a unique solution, when there are no free variables

ii. infinitely many solutions, when there is at least one free variable

Using Row Reduction to Solve a Linear System

1. Write the augmented matrix of the system.

2. Use the row reduction algorithm to obtain an equivalent augmented matrix in echelon form. Decide whether the system is consistent. If there is no solution, stop; otherwise, go to the next step.

3. Continue row reduction to obtain the reduced echelon form.

4. Write the system of equations corresponding to the matrix obtained in step 3.

5. Rewrite each nonzero equation from step 4 so that its one basic variable is expressed in terms of any free variables appearing in the equation.