General Info Geometry Final - Sophomore Year

Topic 5: Congruence in Triangles

Topic 5: Congruence in Triangles

Sum of interior angles of triangle =

180 degrees

Topic 5: Congruence in Triangles

Topic 5: Congruence in Triangles

Sum of interior angles of triangle =

180 degrees

Exterior angle of a triangle =

sum of 2 angles opposite

Equilateral triangle have _ congruent sides and _ angles =

3;3;60 degrees

Isosceles triangles have congruent base angles and _ congruent sides

2

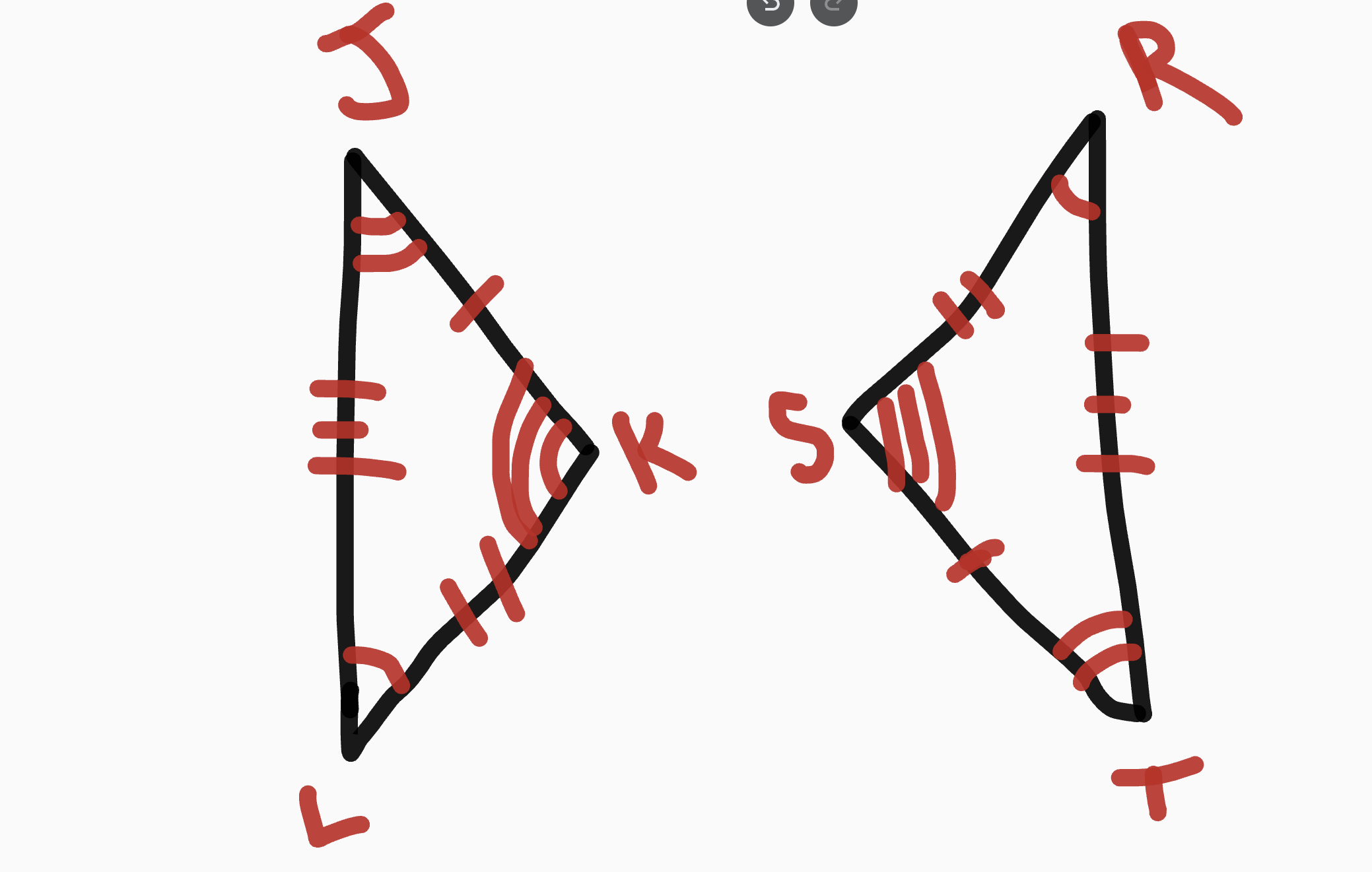
Triangles can be proven congruent by … but never…

SSS, ASA, SAS, AAS and HL

but never AAA or SSA

How to find corresponding sides and angles in congruent triangles PART 1

How to find corresponding sides and angles in congruent triangles PART 2

Topic 6: Relationships between Triangles

Topic 6: Relationships between Triangles

The midsegment of a triangle is

½ of the parallel side

The longest side of a triangle is across from the ___. The smallest side is across from the ___.

largest angle; smallest angle

The two shorter sides of a triangle must add together to be ____.

Larger than the longest side.

Topic 8: Similarity in Triangles

Topic 8: Similarity in Triangles

Triangles can be proven similar by…

AAS, SAS and SSS

Triangles are similar when angles are _ and sides are _

congruent; proportional

How to find corresponding sides and angles in similar triangles

using SSS, ASA, SAS, AAS and HL

but never AAA or SSA

How to use a proportion to solve for the missing side in a similar triangle

The Triangle Proportionality Theorem (The Side Splitter)

Three Parallel Lines Theorem

The Triangle Proportionality Theorem (The Side Splitter)

if a line is parallel to one side of the triangle and intersects the others two sides, then the sides are split proportionally

Three Parallel Lines Theorem

If 3 parallel lines intersect 2 transversals, then they divide the transversals proportionally

If a line parallel to one side of a triangle intersects the other two sides…

then it divides the two sides proportionally.

If three parallel lines intersect two transversals, then they…

divide the transversals proportionally

If a ray bisects an angle of a triangle, then it…

divides the opposite side into segments whose lengths are proportional to the lengths of the other two sides.

Topic 9: Right Triangles & Trigonometry

Topic 9: Right Triangles & Trigonometry

The Pythagorean theorem and how to use it to find missing sides in triangles

Pythagorean theorem is a² + b² = c²

We can use it by plugging in the information we have from the equation, and solving it to find the variable

A 45-45-90 triangle is an _ triangle and has sides that are equal to…

isosceles; x, x, and x√2

A 30-60-90 triangle is _ of an equilateral triangle and has sides that are equal to..

half; x, 1/2x and x√3

If the altitude is drawn to the hypotenuse of a right triangle, then the two triangles formed are…

similar to the original triangle and to each other.

In a right triangle, the altitude from the right angle to the hypotenuse divides the… The length of the altitude is the…

hypotenuse into two segments; geometric mean of the lengths of the two segments of the hypotenuse.

Sine, Cosine and Tangent ratios SOH CAH TOA

Sine = O/H

Cosine = A/H

Tangent = O/A

How to use sine, cosine and tangent ratios to solve for a missing side or angle in a right triangle

How to use sine, cosine and tangent ratios to solve for a missing side or angle in a right triangle

How to use SIN

when you know the H but want to know O

when you know O and H but want an angle

How to use COS

when you know H but want to know A

when you know A and H but want an angle

How to use TAN

when you know A but want to know O

when you know O and A but want an angle

NICE TO KNOW:

NICE TO KNOW:

What is a Pythagorean Triple and how do we find them?

The Pythagorean Triple when all 3 sides area all perfect whole numbers

We find them by using the Pythagorean Theorem

(a² + b² = c²)

What does sine, cosine and tangent mean?

Sine is the Curve (O/H)

Cosine is the opposite curve (A/H)

tangent is to touch (O/A)

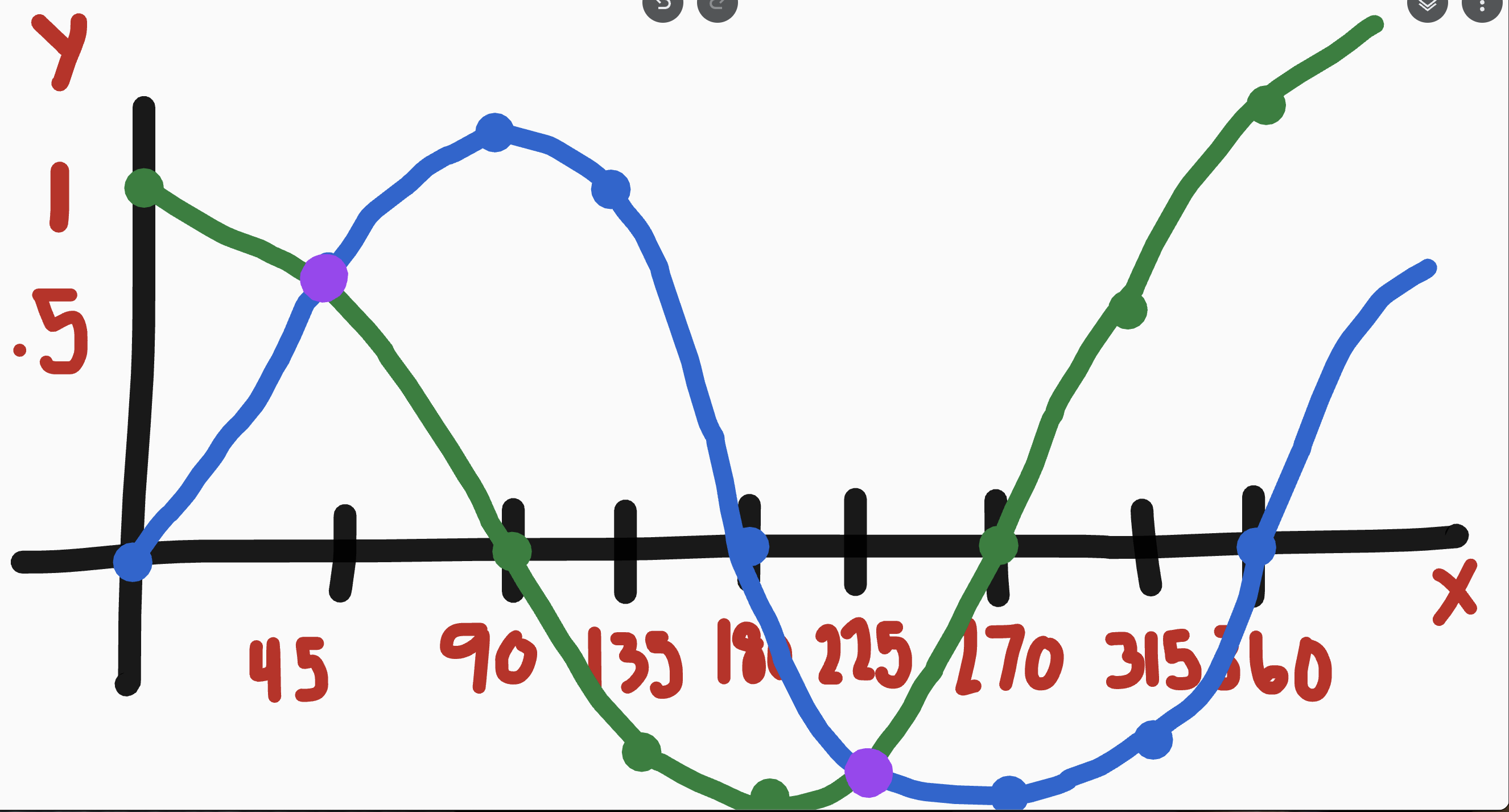
What do the graphs of sine and cosine look like? Why?

They are opposites

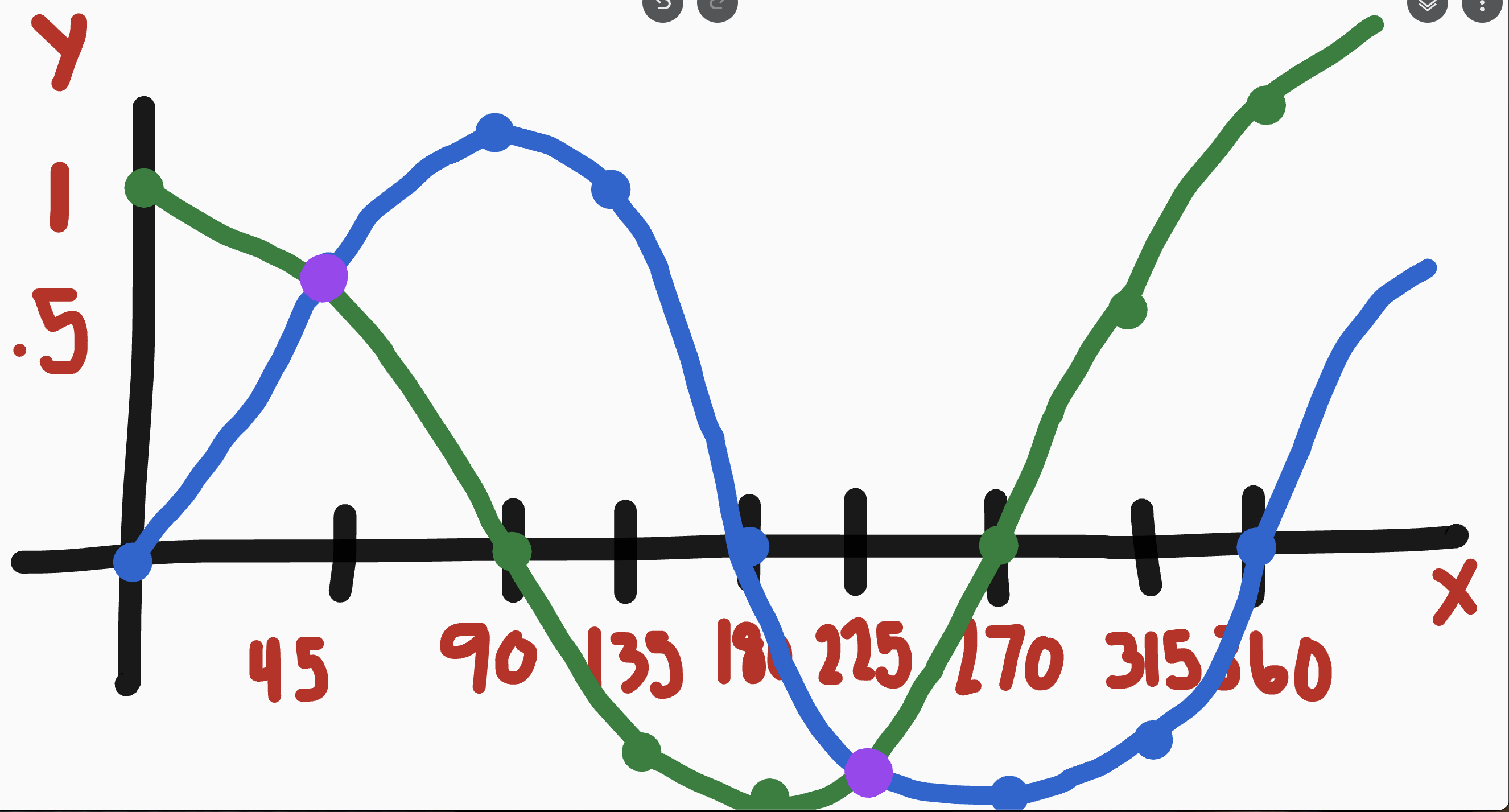
When are sine and cosine equal to one another?

when they equal 90 degrees together

ex: 45 plus 45

60 plus 30