Superposition (Standing waves)

represents amplitude and depends on x (position)

• 2 A sin (kx)

represents SHM

• cos (ωt)

Nodes

• values of x where A = 0

  • y displacement = 0

• these points do NOT move up or down at all (NEVER MOVE)

• occur @ all position (x) multiples of λ/2

  • x = 0, ½ λ, λ, 3/2 λ, 2λ, …

Antinodes

• values of x where A = very large #

  • occur when A of the standing wave is the largest

• occur when x is an odd multiple of λ/4

  • x = ¼ λ, ¾λ, etc.

sin (kx) = ±1

amplitude is largest when?

in a string that is fixed @ both ends, the two ends are nodes

Remember: in a string that is fixed @ both ends, the two ends are nodes

standing waves occur bc of the continuous superposition of waves that are reflected at each end

Remember: standing waves occur bc of the continuous superposition of waves that are reflected at each end

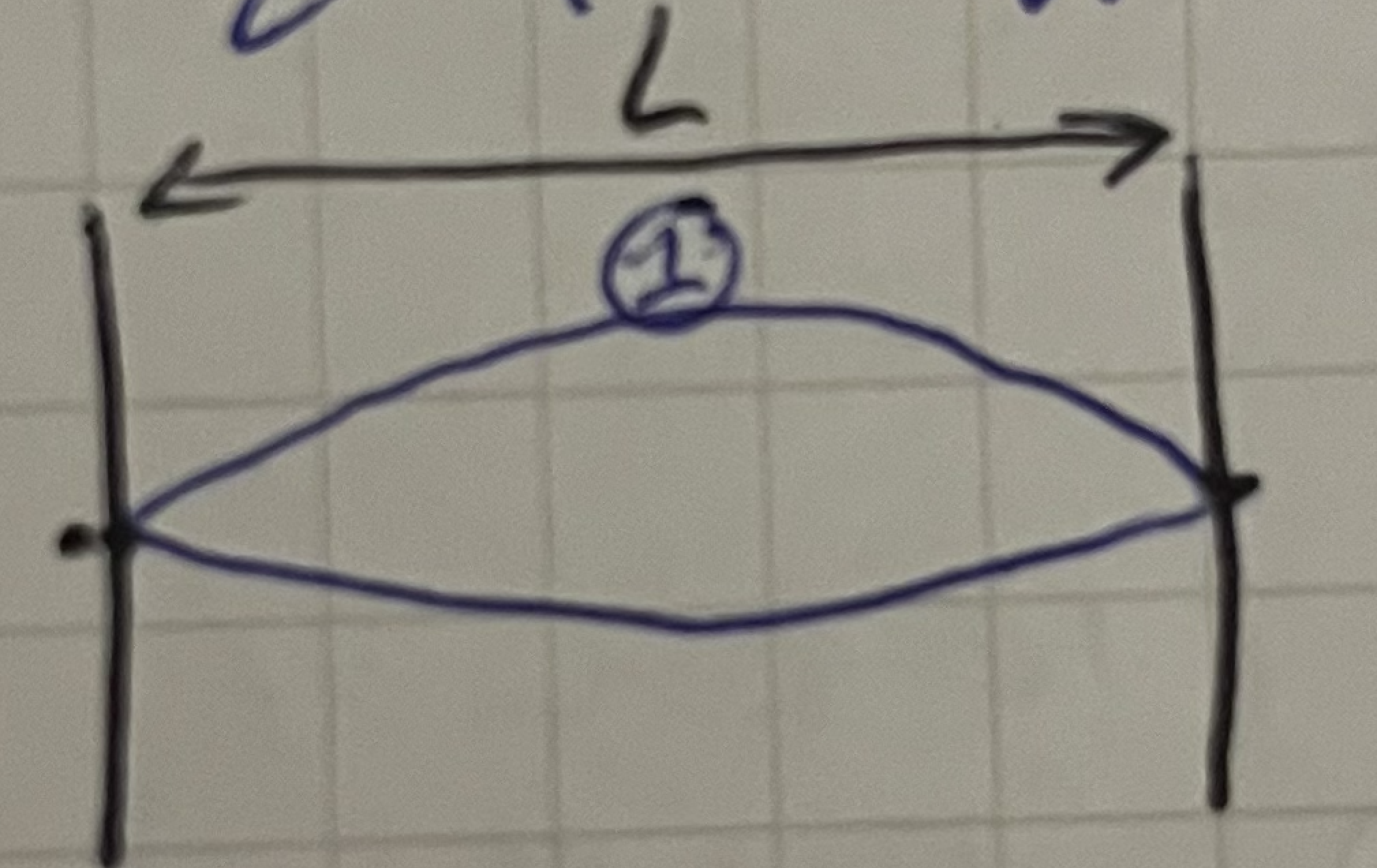
L = ½ λ₁

Given this harmonic mode what is the length of the string equal to?

L = λ₂

Given this harmonic mode what is the length of the string equal to?

L = 3/2 λ₃

Given this harmonic mode what is the length of the string equal to?

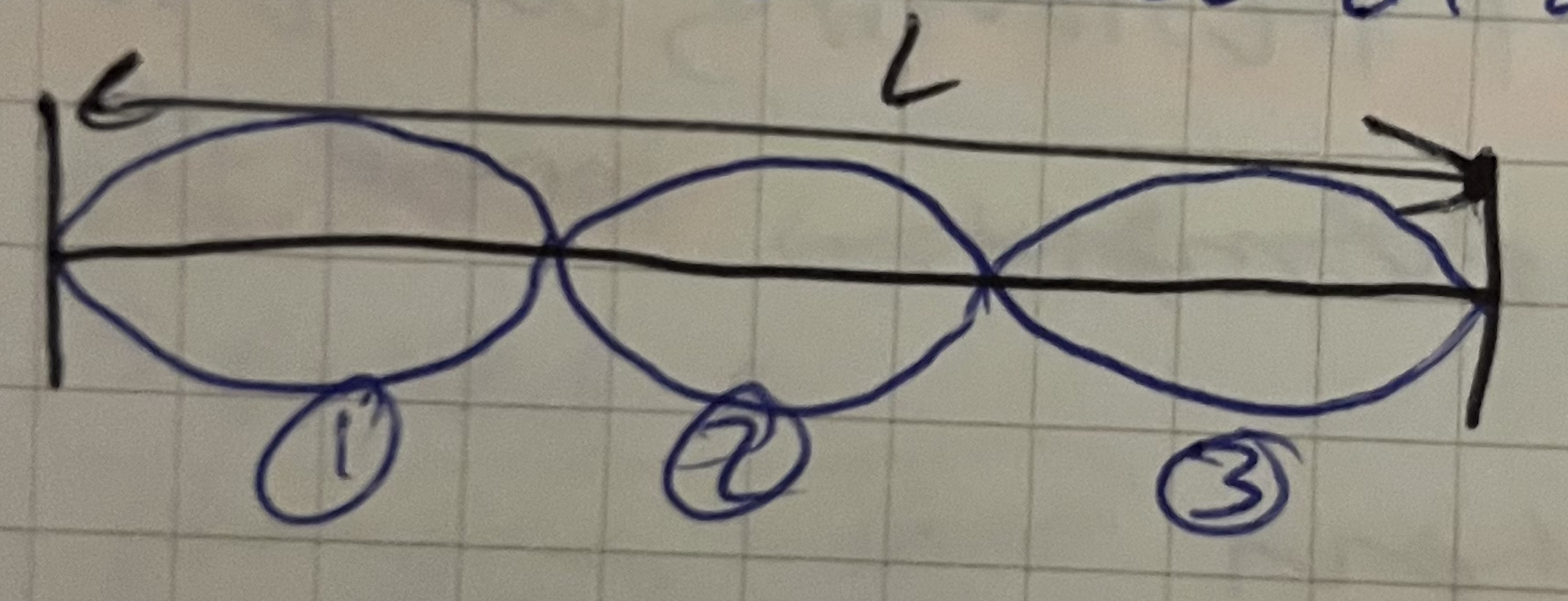
fundamental frequency (f₁)

• f₁ = V / 2L

• can be changes by:

  • changing the strings length

  • changing the strings tension (thus the wave speed)

fm = mf₁

equation for frequency depending on harmonic modes?

Sound waves that oscillate @ diff frequencies, sound diff

Remember: Sound waves that oscillate @ diff frequencies, sound diff

a music note from a string is defined by its fundamental frequency (harmonic mode = 1)

Remember: a music note from a string is defined by its fundamental frequency (harmonic mode = 1)

closed end of pipe

• displacement node

• pressure antinode

open end of pipe

• displacement antinode

• pressure node

open-open pipe

• two pressure nodes

• f₁ = V / 2L

• fm = mf₁

  • m = 1, 2, 3 …

open-closed pipe

• 1 pressure node, 1 pressure antinode

• f₁ = V / 4L

• fm = mf₁

  • m = 1, 3, 5 …

  • m = only odd multiples bc of the antinode