6 - Unsupervised Learning

Uses of unsupervised learning techniques

Exploratory data analysis especially on high dimensional datasets

Feature generation

PCA

To transform a high-dimensional dataset into  a smaller, much more manageable set of representative (“principal”) variables, easier to explore and visualize

PCs are…

linear combinations of the existing variables that capture most of the information in the original dataset

PCA is especially useful for

highly correlated data, for which a few PCs are enough to represent most of the information in the full dataset

PCA score formula

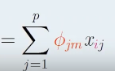
Choose PC loadings to…

capture as much information the original dataset as possible

Goal of PCA for calculations

to maximize the sample variance of Z1

Sample variance formula

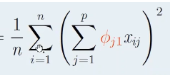
Orthogonality constraints

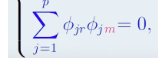
Why are orthogonality constraints needed

so the PCs measure different aspects of the variables in the dataset

PCA analysis is constrained by

the line that is as close as possible to the observations such that minimizes the sum of the squared perpendicular distances between each data point and the line

First and second PCs are…

Mutually perpendicular

Scores formula with notation

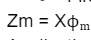
Total variance for a feature

Variance explained by the mth PC

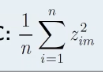
PVE =

Does Centering have an effect on PC loadings? Why?

Centering has no effect on PC loadings because the variance remains unchanged upon centering and this variance maximization is how PC loadings are defined

Does scaling have an effect on PC loadings? Why?

Yes, If variables are of vastly different orders of magnitude, then variables with an unusually large variance on their scale will receive a large PC loading and dominate the corresponding PC

Drawbacks of PCA

• Interpretability: Cannot make sense of the PCs because they are complicated linear combinations of the original features

• Not good for non-linear relationships

  • Uses linear transformations to summarize and visualize high-dimensional datasets where the variables are highly linearly correlates

• PCA is not doing feature selection because all variables go into the components, no operational efficiency added

• Target variable is ignored: Assuming directions in which the features exhibit the most variation are also the directions most associated with the target variable, no guarantee this is true

Scree plot

PVEs against PC index

Are PC loadings unique

Yes, up to a sign flip

Biplot shows what?

the locations of PCAs and scores

How does having categorical variables with high dimensionality hurt a data set?

Predictive power of the model will be diluted and lead to sparse factor levels (those with very few observations)

Suggest 2 ways to transform categorical variables with high dimensionality to retain them

Combine categories into smaller groups

Binarize the two factor variables, run a PCA on each set of dummy variables and use the first few PCs to summarize most of the information

Total SS =

within cluster SS + between cluster SS

Total SS is

the total variation of all the observations in the data without any clustering (essentially there is one large cluster containing all observations)

Between cluster SS

Can be thought of as the SS explained by the K clusters

Two idealistic goals of cluster analysis

• Homogeneity: Want observations within each cluster to share characteristics while observations in different clusters are different from one another

• Interpretability: Characteristics of the clusters are typically interpretable and meaningful within the context of the business problem

PCA/Clustering Similarities

• Unsupervised Learning

• Simplify the data by a small number of summaries

PCA/Clustering Difference

PCAs find low dim representation whereas clustering finds homogeneous subgroups among the obs

K-means clustering algorithm

• Randomly select k points in the feature space as the initial cluster centers

• Assign each obs to closest cluster in terms of Euclidean distance

• Recalc center of each cluster

• Repeat until nothing changes

Why we run K means algorithm multiple times

To mitigate the randomness associated with the initial cluster centers and increase the chance of identifying a global optimum and getting more representative cluster groups

Is K means clustering a global optimum

No, local

Hierarchical Clustering

Series of fusions of observations

Hierarchical clustering algorithm

• Start with all separate clusters

• Fuse closest pair one at a time

  • Repeat until all clusters are fused into a single cluster containing all obs

Within cluster variation vs Euclidian distance

Within cluster is squared for each observation whereas Euclidean distance uses a square root

Elbow method

Choose cutoff where the proportion of variance explained by the k number of clusters reaches the elbow in the graph

Linkage choices

Complete, single, average, centroid

Complete linkage

Single linkage

Minimal pairwise distance

Average linkage

Average of all pairwise distances

Centroid linkage

Distance between the two cluster centroids (or centers)

Most common linkage methods? Why?

Complete and average because they result in more balanced and visually appealing clusters

Dendrogram

an upside down tree that shows dissimilarity at each fusion

Lower cut dendrogram results in _____ clusters

More

Differences of K means and hierarchical

Randomization

Pre-specified number of clusters

Nested clusters

Which of K means and hierarchical need randomization?

K means

Which of K means and hierarchical need pre-specified clusters?

K means

Which of K means and hierarchical need nested clusters?

Hierarchical

Similarities of K means and hierarchical

• Both unsupervised

• Objective is to uncover homogeneous subgroups among the observations

• Both are sensitive to scaling of variables

• Both are sensitive to outliers

Solution for observations with largely different scales

correlation based distance

Ways to generate features from cluster analysis

• Cluster groups

• Cluster centers can replace the original variables for interpretation and prediction purposes

Two impacts of Curse of dimensionality for clustering

Harder to visualize data

Notion of closeness becomes more fuzzy when there are more and more variables

Which linkage can results in inversion

Central linkage

Considerations for number of clusters to choose for hierarchical clustering

Balance

Height differences

Explain two reason why unsupervised learning is often more challenging than supervised learning

Less clearly defined objectives

Less objective evaluation

Why are PC loading vectors unique up to a sign flip

The line of the PC extends in both directions and therefore gives rise to another valid PC loading vector

Explain how scaling the variables will effect the results of clustering

Unscaled variables might have one dominate the distance calculations and exert a disproportionate impact on the cluster arrangements, so we adjust for that

Explain how principal components analysis can be used as a pre-processing step before applying clustering to a high-dimensional dataset

PCA can allow us to compress the data into 2 dimensions without losing much information and to visualize the cluster assignments in a two-dimensional scatterplot using the scores of the first two PCs

Large variance for PC1 and small others imply what?

Strong correlation among the variables

What is the name of the plot for K means clustering

Elbow plot

When to select for an elbow plot

When it levels off

State the difference between dissimilarity and linkage

Dissimilarity measures the proximity of two observations in the data set, while linkage measures the proximity of two clusters of observations

Describe the steps to calculate the within cluster sum of squares using latitude and longitude

Calc the centroid

Calc sq Euclidean distance between each city and the respective centroid

Sum all sqd distances

What distance method does K means clustering and hierarchical clustering use

Euclidean