Statistika - jaký test kdy použít a další věci

metrická x metrická

test Pearsonova korelačního koeficientu

(potřebuju normální rozděleni)

metrická x ordinální

test Spearmanova korelačního koeficientu

metrická x nominální

ANOVA (potřebuju normální rozdělení + shodu rozptylů)

Welshova ANOVA (potřebuju normální rozdělení)

metrická x alternativní

t-test pro dva nezávislé výběry (potřebuju normální rozdělení + shodu rozptylů)

Welshův test (potřebuju normální rozdělení)

metrická x konstanta (zadané četnosti)

t-test pro jeden výběr (potřebuju normální rozdělení)

ordinální x ordinální

test Spearmanova korelačního koeficientu

ordinální x nominální

Kruskalův - Wallisův test

ordinální x alternativní

Mann-Whitneyův U-test = Wilcoxonův dvouvýběrový test

ordinální x konstanta

Wilcoxonův jednovýběrový test (znaménkový test)

nominální x nominální

chí kvadrát test nezávislosti (potřebuju minimální očekávanou četnost)

chí kvadrát test homogenity (potřebuju minimální četnost)

nominální x alternativní

chí kvadrát test nezávislosti (potřebuju minimální očekávanou četnost)

chí kvadrát test homogenity (potřebuju minimální četnost)

nominální x konstanta

chí kvadrát test dobré shody (potřebuju minimální očekávanou četnost)

alternativní x alternativní

chí kvadrát test nezávislosti (potřebuju minimální očekávanou četnost)

chí kvadrát test homogenity (potřebuju minimální očekávanou četnost)

(Fisherův faktoriálový test)

alternativní x konstanta

chí kvadrát test dobré shody (potřebuju minimální očekávanou četnost)

(užití binomického rozdělení)

co dělat když potřebuju minimální očekávanou četnost (chí kvadrát testy)

=> pokud není reálná četnost alespoň taková jako očekávaná četnost => sloučím kategorie

=> pokud ani to nepomůže => převedu na alternativní proměnou => když ani to nejde => Fisherův faktoriálový test

nominální proměnná

je to jen “nálepka”, nedají se srovnat, co je >/<

rozlišíme je mezi sebou (Karel není to stejné co Petr)

alternativní proměnná

má pouze dvě možnosti (0 a 1)

ordinální proměnná

dá se srovnat, kdo má míň/víc, ale nedokážeme říct, jak velký je mezi nimi rozdíl (např. časový rozdíl doběhu prvního a druhého závodníka = nevíme)

metrická proměnná

př. věk, výška, IQ

nemusíme rozlišovat intevalovou a poměrovou => vše je metrická

konstanta

u všech lidí je to stejné - př. nikdo nemá diagnózu

p-hodnota

pravděpodobnost, že při platnosti nulové hypotézy nám vyjde něco, co takhle moc a víceporušuje

nulová hypotéza - co s výsledkem?

můžeme ji pouze ZAMÍTNOUT

alternativní hypotéza - co s výsledkem?

můžeme ji pouze PŘIJMOUT

jednostranné hypotézy

• v hypotéze je “méně” => p-hodnota = 1-(p/2)

• v hypotéze je “více” => p-hodnota = p/2

dvoustranné hypotézy

p-hodnota, co mi vyjde je výsledek

hypotézy o rozdílu

t-test (single sample)

t-test pro jeden výběr

=> basic statistics- t-test, single sample

• srovnává střední hodnoty (průměr našeho jednoho náhodného výběru oproti zadané konstantě)

• testová statistika: T

• rozdělení: Studentovo t-rozdělení

• míra účinku: d (v kolika směrodatných odchylkách se liší od nulové hypotézy) ((s = odhadnutá směrodatná odchylka))

párový t-test

=> basic statistics- t-test, dependent samples

• aplikujeme na proměnné, které NEJSOU nezávislé => předpokládáme, že se “ovlivňují navzájem” (typicky výsledky pretest-posttest; rozdíl dělání věcí levou a pravou rukou,…)

• přesně totéž co jednovýběrový test aplikovaný na sloupečku rozdílů hodnot (například druhé měření mínus první měření)

• také srovnává střední hodnotu (ovšem průměr sloupečku rozdílů) oproti očekávané změně dané nulovou hypotézou – tedy 0 („žádná změna“, „zlepšení není“)

• míra účinku D, kde D s čarou je průměrné zlepšení, mý D0 je 0, Sd je směrodatná odchylka sloupce “zlepšení”

  • nebo taky d= průměr D/Sd nebo průměr D/Sx (= tak, jak je to v populaci)

dvouvýběrový t-test (t-test pro dva nezávislé výběry)

=> basic stat.- t-test, independent

• by variable znamená, že vybereme jeden sloupec dat jako jednu skupinu a druhý sloupec dat jako druhou skupinu - máme skupiny každou v jiném sloupci

• by group znamená, že stanovujeme jednu proměnnou, jejíž úrovně budou stanoveny jako skupiny, a druhou dependent/závislou proměnou => když máme jeden sloupec dat čistě 0/1 (experimentální/kontrolní) a druhou jako sloupec bodů

• testuje shodu dvou středních hodnot (průměry dvou skupin), které jsou na sobě nezávislé, a předpokládá, že skupiny mají stejné rozptyly

• například: jak skórují v testu lidi ve skupině A a ve skupině B

• testová statistika: T

• rozdělení: Studentovo t-rozdělení

• míra účinku: Cohenovo d X jednodušší cesta: získat ji přímo ze statistiky T a rozsahů skupin n a m:

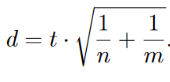
Welchův test (t-test pro 2 nezávislé výběry bez předpokladu shody rozptylů)

=> basic stat.- t-test, independent, v kolonce options zaškrtnout t w/separate variance estimates

• testuje shodu středních hodnot (průměry dvou skupin) na dvou výběrech, které jsou nezávislé, když rozptyly nemusejí být stejné

• testová statistika: T

• rozdělení: Studentovo t-rozdělení

• míra účinku:

  • Glassova delta (pokud dokážeme určit, která ze skupin je kontrolní – typicky u experimentálních designů)

    • Glassova Δ= (průměr skupiny X - průměr skupiny Y)/ směrodatná odchylka kontrolní skupiny (třeba Y zrovna)

  • nebo opět Cohenovo d (pokud nelze určit, která ze skupin je kontrolní – typicky např. muži ženy)

    • Cohenovo d= stejné jako glassova delta, jen dělím směrodatnou odchylkou obou skupin smíchaných dohromady

F-test

=> basic stat.- t-test, independent, samo to udá i F

• testuje shodu rozptylů dvou skupin (Statistica jej počítá automaticky společně s dvouvýběrovým t-testem/ t-testem pro dva nezávislé výběry) (je to jakoby něco navíc, nikdy to není ten test z tabulky, kterým bych testovala hypotézu)

• například: jsou skóry mužů a žen stejně variabilní? Skórují ženy i muži v testu v rozmezí 5-25 bodů nebo je u některé skupiny rozmezí větší/menší?

• testová statistika: F

• rozdělení: Fisherovo rozdělení

• míra účinku: neuváděli jsme si žádnou, protože se F test sám o sobě moc nepoužívá (funguje na něm ANOVA)

test Pearsonova korelačního koefiientu

=> basic stat.- correlation matrices-&gt; options, display r, p-values and N´s

• testuje souvislost dvou proměnných oproti očekávané korelaci, která je nulová (proto se dialog ve Statistice jmenuje „test nulovosti korelačního koeficientu“)

• testová statistika: T

• rozdělení: Studentovo t-rozdělení

• míra účinku: samotný korelační koeficient (r), popř. koeficient determinance (r²)

Co dělat, když chceme mezi sebou srovnávat více než 2 skupiny?

můžeme použít sérii každý s každým, ale problém je potom s p hodnotami (při jednom testu je 5% šance, že bude zamítnuta nulová hypotéza, ale když jich provedeme více, tahle chybovost stoupá), takže musíme aplikovat Bonferroniho korekci => upravíme p hodnotu tak, že ji vydělíme počtem možných kombinací testů

jednofaktorová/jednocestná ANOVA (analýza rozptylu při jednoduchém třídění – všechno jsou to synonyma)

=> ANOVA- one way => quick => all results

• analýza rozptylu - metoda na test hypotézy o středních hodnotách

  • one-way ANOVA => analýza rozptylu při jednom rozptylu

• srovnává střední hodnoty skupin, kterých je více než 2 a které mají stejné rozptyly (pokud máme dvě, sáhneme po t-testu pro 2 nezávislé výběry; ANOVA je tedy zobecněním tohoto t-testu pro případy, kdy máme skupin vícero)

• ANOVA funguje na principu dvou způsobů odhadů rozptylů, které jsou mezi sebou následně porovnány

  • za předpokladu nulové hypotézy (=mezi skupinami není rozdíl) odhadují rozptyl stejně

  • za předpokladu alternativy (=mezi skupinami je rozdíl) jeden způsob odhadu nadhodocuje a to odhalí Fisherův F test

• testová statistika: F

• rozdělení: Fisherovo rozdělení

• míra účinku: není potřeba znát, neuváděli jsme si žádnou

• shoda rozptylů se počítá přes Levenův test

Welchova ANOVA

=> basic statistics => breakdown and one way ANOVA => ANOVA and tests => zaškrtni Welch´s F test => analysis of variance

• srovnává totéž, co klasická jednofaktorová ANOVA, jen si neklade podmínku shody rozptylů (tím pádem je asi lepší použít Welchovu ANOVU než obyč. ANOVU)

• testová statistika: F

• rozdělení: Fisherovo rozdělení

• míra účinku: není potřeba znát, neuváděli jsme si žádnou

Leveneův test

=> basic statistics => breakdown and one way ANOVA => ANOVA and tests => Levene tests

• test, který dokáže rozhodnout o shodách rozptylů náhodých veličin, které porovnáváme

• v ANOVĚ => pokud bychom potřebovali rozhodnout, jestli použít ANOVU (protože máme stejné rozptyly) nebo použít Welchovu ANOVU (protože nemáme stejné rozptyly)

• Výzkumná otázka by tedy byla: Existuje v rozptylech rozdíl?

• nulová hypotéza: mezi rozptyly není rozdíl

Post-hoc testy (po ANOVĚ)

• odpovídají na otázku “MEZI KTERÝMI skupinami je rozdíl?” => ANOVA odpovídá pouze na otázku, JESTLI je mezi skupinami rozdíl a to formou ANO/NE (=je/není porušena nulová hypotéza)

• Tukey a Sheffé

Tukeyho HSD test (=honest significant difference)

=> ANOVA- one way => more results (vlevo dole) => post-hoc => Tukey HSD

• silný při malém počtu skupin, s rostoucím počtem skupin ztrácí citlivost= pak už v podstatě nezamítne žádnou nulovou hypotézu, ať už platí nebo ne

Scheffého test

=> ANOVA- one way => more results (vlevo dole) => post-hoc => Scheffe

• slabší než Tukey, není moc vhodný pro málo skupin, pro hodně skupin je naopak velice dobrý

• ideálně zkusit oba

testy normality - Shaphir-Wilkův test

• testují hypotézu o tom, jestli pochází veličina z normálního rozdělení

• alternativa říká, že veličina nepochází z normálního rozdělení

• statistické programy nabízejí více testů (Kolmogorův-Smirnovův test, Lilieforsův test)

Shapirův-Wilkův test

• graphs => histograms => advanced => Shapiro-Wilk test

• (nebo Descriptive statistics => Normality)

• považován za nejsilnější z testů normality

• podle p-hodnoty poznám, zda je to normální nebo ne (H0 = je to normální; když je malá p-hodnota, nepochází to z norm. rozdělení)

analýza síly testu

• síla testu říká, zda je metoda náchylná k rozpoznání porušení nulové hypotézy či ne

• silný test= citlivý na porušení nulové hypotézy (= je porušena, test to zjistí)

• slabý test= není citlivý (nulová hypotéza porušena, test to nezjistí)

• výsledkem je číslo v intervalu od 0 do 1, které znamená následující: například 0,5 znamená, že náš test potřebuje 100 lidí, aby odhalil porušení nulové hypotézy, zatímco t-testu by jich stačilo 50 (což je velký rozdíl) = slabý test

• NEBO 0,96 => t-test by to zvládl s 96 a my potřebujeme 100 (což není skoro žádný rozdíl) = silný test

analýza síly testu - postup

=> statistics => power analysis => power calculation => t-test, dva nezávislé => “Mu= střední hodnota”, “n1 a n2= rozsahy souborů”, “sigma=směrodatná odchylka souborů” => calculate power

poznámka: pokud nejsou zadány střední hodnoty a směrodatná odchylka, ale Cohenovo d například 0,8, doplníte jakékoli hodnoty Mu1, Mu2 a Sigma, aby vyšlo 0,8 =&gt; nejjednodušší je 0,8, 0 a 1 =&gt; (0,8-0)/1= 0,8

=> statistics => power analysis => power calculation => one correlation => “Rho= očekávaná míra korelačního koeficientu, N= počet dvojic” => nalevo dole zakliknout “fisher Z Crude” => calculate power

převádění p-hodnot

• statistika nám vždy dá oboustranné p hodnoty (nulová hypotéza říká, že mezi skupinou A a B není rozdíl, zatímco alternativa říká že rozdíl je, ale neříká jaký)

• pokud chceme jednostrannou p hodnotu (například místo “mezi skupinami je rozdíl” testujeme hypotézu “skupina A má vyšší skór než B”), jsou dvě situace:

1. vyjde to ve směru, jaký udává alternativa (skupina A skóruje lépe než B, zjistíte třeba z mediánu u neparametrických nebo z průměrného skóru u parametrických) => pouze vydělíte p hodnotu dvěma => p/2

2. vyjde v opačném směru než říká alternativa (“A jsou lepší než B” ale v datech vidíte Mean(A)= 30 a Mean(B)=59) => p hodnotu vydělíte dvěma a odečtete od jedničky => 1-(p/2)

testy četností

• testy chí kvadrát (test dobré shody, test nezávislosti, test homogenity)

• Fisherův exaktní faktoriálový test

• McNemarův test

testy chí kvadrát

• testová statistika: vždy Z (ve Statistice nazýváno jako Pearsonův chí kvadrát)

• rozdělení: chí kvadrát rozdělení (= Pearsonovo rozdělení… proto ten název výše)

• míra účinku: koeficient fí

• patří tam:

  • test dobré shody

  • test nezávislosti

  • test homogenity

test dobré shody (pro jeden výběr)

• test četnosti

  => basic statistics => frequency tables => přidáme sloupec s očekávanými četnostmi

  podle teorie => vypočítáme, jaké by měly být četnosti v našem souboru, aby byly v

  souladu s teorií (rozsah souboru*teoretická četnost) => uděláme si z workbooku základní data => nonpar-=> observed versus expected X2 => vybereme pozorované a očekávané => summary

• použijeme v situaci, kdy máme nominální náhodnou veličinu X o k úrovních a

  ověřujeme nulovou hypotézu, která stanovuje pravděpodobnosti výskytu

  jednotlivých úrovní

• Například: teorie říká, že ve společnosti je 50% heterosexuálů, 20%

  homosexuálů, 10% bisexuálů, 10% pansexuálů a 10% lidí dalších sexuálních

  menšin => ověřuji, zda můj soubor podporuje tuhle teorii, zda realita

  odpovídá teorii

chí kvadrát test nezávislosti

=> basic stat. => tables and banners (kontingenční tabulky) => ok => options => expected frequencies (zkontrolovat že jsou nad 5) => options => Pearson & M L Chi square => překliknout na záložku advanced => detailed two way table => (může se objevit “vyčíslete závislost mezi alternativní a nominální proměnou, v tom případě zaškrtneme kromě Pearsona ještě Phi)

• použijeme, když se snažíme zjistit zda existuje souvislost mezi dvěma náhodnými veličinami (my je neovlivníme), které jsou nominálními proměnnými (například: zda si lidé volí terapeuty z různých škol podle diagnózy, poznámka: to, že jsou obě proměnné náhodnými veličinami bychom zajistili tak, že bychom napřed kontaktovali lidi, kteří mají teprve v plánu jít na terapii a ptali se jich na problém, následně bychom je kontaktovali po nějaké době a teprve zjišťovali zaměření terapeuta => pokud bychom se zkrátka jen ptali lidí, kteří už jsou u nějakého terapeuta na problémy, byl by to test homogenity nikoli nezávislosti)

• nulová hypotéza: jsou nezávislé= nesouvisí spolu (úzkostní nehledají častěji KBT terapeuta než logoterapeuta)

• podmínka: očekávané četnosti > 5

• Yatesova korekce= udělá test konzervativnějším, řeší problém toho, že test nezávislosti nerespektuje zcela přesně stanovenou hladinu α a zamítá nulovou hypotézu o něco častěji, než požadujeme (na stejném místě jako Pearson & M L Chi square)

• míra účinku: koeficient fí

chí kvadrát test homogenity

=> basic stat. => tables and banners (kontingenční tabulky) => ok => options => expected frequencies (zkontrolovat že jsou nad 5) => options => Pearson & M L Chi square => překliknout na záložku advanced => detailed two way table

• použijeme, když se snažíme zjistit vztah dvou nominálních proměnných, ale jen jedna z nich je náhodnou veličinou (ptáme se 50 lidí od terapeuta KBT, 50 lidí od logoterapeuta a 50 lidí od psychoanalytika na problémy => problém je zde náhodnou veličinou, zaměření terapeuta ne, to jsme si stanovili my) => zjišťujeme, zda jsou u všech terapeutů problémy rozložené stejně

• nulová hypotéza: mezi veličinami není vztah, jsou na sobě nezávislé

• opět problém s nízkými četnostmi, očekávané nesmí být menší než 5

• míra účinku: koeficient fí (na stejném místě jako Pearson…, jmenuje se “Phi (2x2)”)

• když jsou zafixovány marginální četnosti, zda je to ve všech skupinách stejné

• je to jakoby test nezávislosti v jiném kontextu (kliká se to v programu úplně stejně)

Fisherův exaktní faktoriálový test

=> basic stat. => tables and banners (kontingenční tabulky) => ok => options => expected frequencies (zkontrolovat že jsou nad 5) => options => jak je Pearson & M L Chi square tak dám Fisher extact => překliknout na záložku advanced => detailed two way table

• testy nezávislosti a homogenity nepracují příliš dobře, pokud máme malé očekávané četnosti, to řeší tento test, v podstatě se jedná o test nezávislosti/homogenity pro čtyřpolní (2x2) kontingenční tabulku => použijeme ho, pokud máme alternativní a alternativní proměnnou

  • použiju ho při opravdu malých očekávaných četnostech (menší než 5), když mám alternativní proměnné

• nulová hypotéza: náhodné veličiny jsou na sobě nezávislé (není mezi nimi vztah)

• nemá testovou statistiku, tudíž ani nevede k žádnému rozdělení

• vrací pouze p-hodnotu (získanou přesným kombinatorickým výpočtem) (to je ta hodnota v řádku: Fisherův p - při jednostranné hypotéze to bude ten řádek výš (nebo Fisherův p/2)

McNemarův test

=> basic stat. => tables and banners (kontingenční tabulky) => ok => options => expected frequencies (zkontrolovat že jsou nad 5) => options => jak je Pearson & M L Chi square tak dám McNemar (je to u Fishera) => překliknout na záložku advanced => detailed two way table

• když máme dvě závislá měření (například pretest- posttest, klasicky bychom použili párový t test), ale na alternativních proměnných => použijeme čtyřpolní kontingenční tabulku

• nulová hypotéza: měření, která měla původně 0 a následně 1, je stejně, jako měření, která měla původně 1 a poté 0

• příklad: snažíme se zjistit, zda přednáška statistiky k něčemu byla, dáme proto studentům příklad před začátkem hodiny a zaznamenáme, zda jej vyřešili (1) nebo nevyřešili (0), poté je necháme jít na přednášku a po přednášce jim znovu zadáme příklad a sledujeme, zda jej byli schopní vyřešit (1) či nikoliv (0) => snažíme se zjistit, jestli lidí, kteří před přednáškou neuspěli a po ní ano (0 => 1), je stejně jako těch, co před uspěli a poté ne (1 => 0) (=což by znamenalo že úspěch a přednáška spolu nesouvisejí a přednáška byla úplně k hovnu)

• podmínka testu: počet případů 0;1 a případů 1;0 musí být dohromady osm nebo více

neparametrické testy

pokud pracujeme s náhodnými veličinami, které nemají známé rozdělení (nedá se říct, že by měli normální, binomické, chí kvadrát,...) => tím pádem bychom nebyli schopni je popsat za pomoci několika parametrů jako doteď (nestačila by nám třeba střední hodnota a rozptyl)

jednovýběrový znaménkový test + jednovýběrový Wilcoxonův test

párový znaménkový test + párový Wilcoxonův test

=> znaménkový test => nonpar => comparing two dependent samples => sign test

=> znaménkový test přes binomické rozdělení => zjistíte N (přes deskriptivní statistiky) => uděláte si sloupec rozdílu (proměnná 1 - proměnná 2)=> zjistíte, kolik čísel je + a kolik - => pro binomické rozdělení potřebujete menší z těchto čísel (X), celkový počet N a pravděpodobnost (P, u binom je to 0,5) => statistics => calculators => distributions => binomial => zadáte hodnoty X, N a P a vypočítá vám to JEDNOSTRANNOU p hodnotu (musíte násobit 2)

=> Willcoxon => nonpar => comparing two dependent samples => Wilcoxon Matched pairs test

• tytéž testy, jen Wilcoxon je o něco silnější (znaménkový test je téměř nejslabší ze všech= není citlivý k porušení nulové hypotézy)

• jsou stejné jako jednovýběrové testy aplikované na sloupečku rozdílů

• oba ověřují odlišnost mediánu sloupečku rozdílů od hodnoty zadané nulovou

• hypotézou – tedy 0 („žádná změna“), pokud se v souboru nacházejí hodnoty rovné mediánu, jsou vyřazeny => znaménkový test zajímá pouze to, zda jsou hodnoty v našem souboru (sloupečku rozdílů) menší/větší než medián daný nulovou hypotézou (0) => Wilcoxonův test = pořadový neparametrický test, určí vzdálenost našich hodnot od mediánu (u párového 0), sečte pořadí hodnot, které jsou pod mediánem a nad mediánem, předvede na normální rozdělení a vrátí p hodnotu, funguje ale jen v případě, že mají obě veličiny stejná rozdělení pravděpodobnosti

• Wilcoxon funguje pouze na symetrické hodnoty

Mann-Whitneyův U-test = dvouvýběrový Wilcoxonův test

=> nonpar => comparing two independent samples (groups) => Mann-Whitney U test

=> pokud chceš p-hodnotu s korekcí jak na spojitost tak na shody v měření, je to p za Z adjusted

• tytéž testy (Statistica nám však rozhodování ulehčila tím, že nám Wilcoxona ani nenabízí; zná pouze Mann-Whitneyův U test)

• použijeme jej v situaci, kdy bychom pro parametrické použili t-test pro dva nezávislé výběry

• testují hypotézu, že pravděpodobnost, že náhodně vylosovaný prvek z jedné skupiny skóruje výše než náhodně vylosovaný prvek z druhé skupiny, je stejná jako ta, že tomu bude naopak (prvek z první skupiny bude skórovat níž než ten z druhé skupiny)

• testová statistika: U, kterou převádíme na statistiku Z

• rozdělení: normované normální

• míra účinku: AUC (area under curve, stochastická dominance), pořadově-biseriální korelace, Hodgesův-Lehmannův estimátor, …

  • AUC: U/nm, kdy n a m jsou rozsahy obou souborů (nebo 1-(U/nm), záleží, kterou potřebujeme, jestli pro X nebo pro Y)

test Spearmanova korelačního koeficientu

=> nonpar => correlations (spearman, kendall tau, gamma)

• když chceme zjistit sílu závislosti mezi kvantitativními proměnnými, které nemají normální rozdělení, nebo pro ordinální proměnné

• testová statistika: T

• rozdělení: Studentovo t-rozdělení

• míra účinku: samotný korelační koeficient (r s )

Kruskal-Wallisův test (Kruskal-Wallisova ANOVA)

=> statistics => nonpar => comparing multiple independent samples (groups) => Kruskal Wallis ANOVA & Median test

• zobecnění Mann-Whitneyova testu pro více než 2 skupiny = neparametrická ANOVA

• testuje hypotézu, že když náhodně vylosuju jeden prvek z jedné skupiny, jeden prvek z druhé skupiny až jeden prvek z k-té skupiny, tak alespoň jeden z těchto prvků se bude svou hodnotou lišit

• testová statistika: H

• rozdělení: chí kvadrát

• míra účinku: není potřeba znát, neuváděli jsme si žádnou

parametrické a neparametrické testy - tabulka

volba testu krok za krokem

1. identifikovat ty dvě proměnné

2. identifikovat úrovně těch dvou proměnných

   • konstanta- neměnící se číslo

   • alternativní- 2 možnosti => muži/ženy, s terapií/bez, blond/jiná barva vlasů,...

   • nominální- více než dvě možnosti, často kvalitativní, nejde je seřadit =>

     oblíbené příchutě zmrzliny, jaké bere participant léky, jakou podstupuje terapii,..

   • ordinální- více než 2, jde je seřadit, ale nejsou mezi nimi stejné intervaly => typicky jak rychle někdo dopsal test (odevzdá první, druhý odvzdá 10 minut po něm, třetí minutu po něm => mám pořadí, ale “vzdálenosti” nejsou stejné)

   • metrické- čísla, jde se seřadit => typicky skóry testů, tváříme se že i

     psychologických

   • všechny si můžu kdykoli “snížit” na nižší úroveň (metrická => ordinální => nominální => alternativní; př.: skór v testu => pořadí od nejlepšího po nejhoršího; vanilková, čokoládová, pistáciová=> vanilková x jiná)

3. podle tabulky (v hlavě) a podle úrovní těch dvou proměnných vybereme test

pretest x posttest a dva skóry => jaký typ testu použiju?

• dva skóry se tváří jako metrické, nemůžeme je tak brát

• test funguje tak, že si hodnoty odečte a porovnává je s předpokládaným zlepšením, což je nula (protože nulová hypotéza předpokládá, že mezi skupinami není rozdíl) => není to tedy například metrická x metrická, ale metrická x konstanta

• párový t-test (t-test pro jeden výběr)

vypočítejte shodu/rozdíl rozptylů - co vlastně budu počítat?

• u párového testu se mi rovnou vypočítá statistika F

• u ANOVY použiju Levenův test

• u Pearsona jen hodím r na druhou (=koef. determinace)