Inverse, Rank, and Null Space - Matrix Algebra

What is the matrix setup for solving a linear set of equations?

A is the scalars, the vector x are the basis vectors, and the vector v is the constants from that linear set of equations.

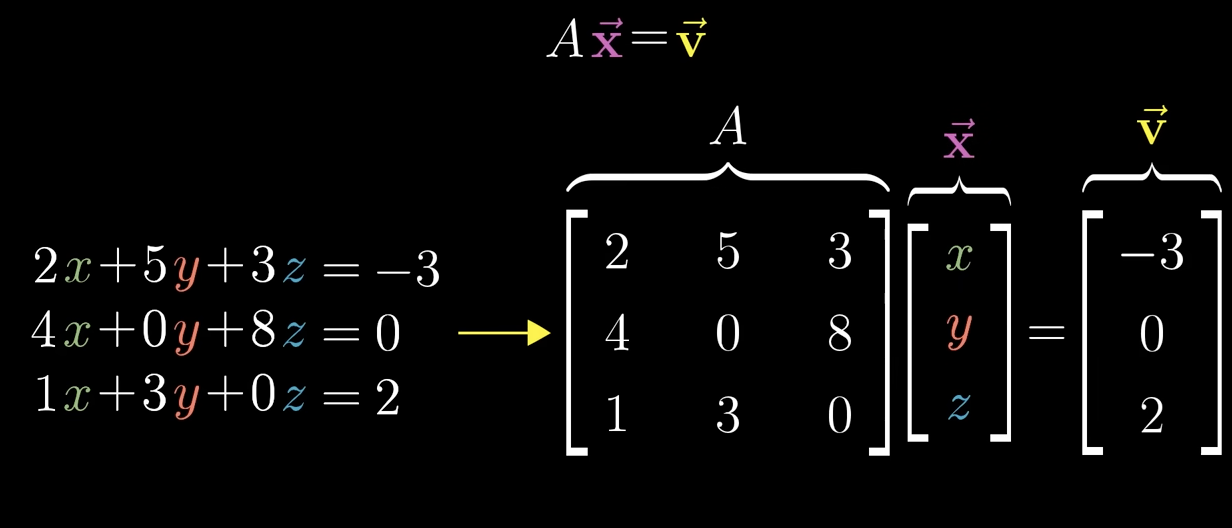
When breaking the equation down (Ax=v or b) What does each term mean?

A corresponds to some linear transformation. x is the vector were looking for after applying the transformation that lands on v.

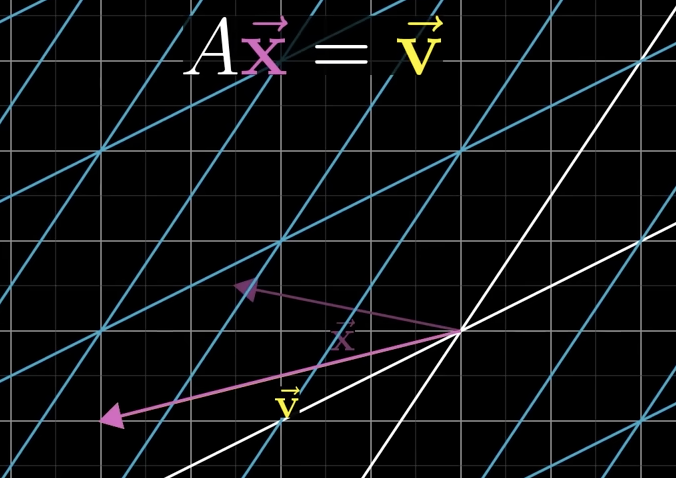
How should we think about multiple variable equations?

Just by squishing and morphing space and trying to figure out which vector lands on another.

What happens when the space detA does not = 0.

In this case there will always be one and only one vector that lands on v. You can find it by playing the transformation in reverse.

What happens when you play the transformation in reverse?

This is what we call the inverse transformation.

If a matrix A was a 90 degree counter-clockwise rotation, what would its inverse be.

The inverse would be a 90 degree clockwise rotation

If matrix A was a rightward shear that pushes j hat one unit to the right, what would the inverse transformation be?

The inverse would be a leftward shear that pushes j hat one unit to the left.

What is the transformation that does nothing?

That is called the identity matrix

What does an inverse matrix do?

It reverse the transformation: it brings vectors back to where they started.

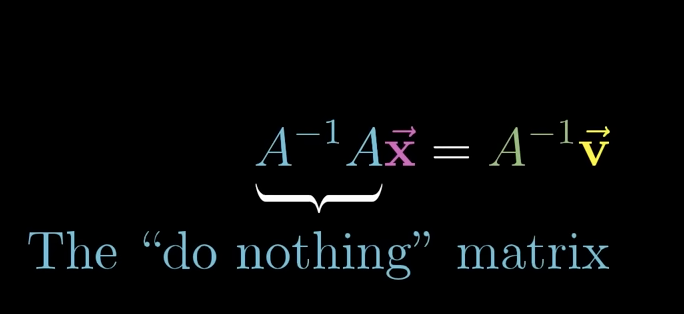
When does a matrix have an inverse?

Only when it does not flatten any dimension (Ex. det does not = 0 and colums are linearly independent).

What does it mean if a matrix is not invertible?

It squishes some directions to 0 (completely flat), so you cannot undo the transformation.

Some vectors different from zero all get mapped to the same point, so you cannot go back.

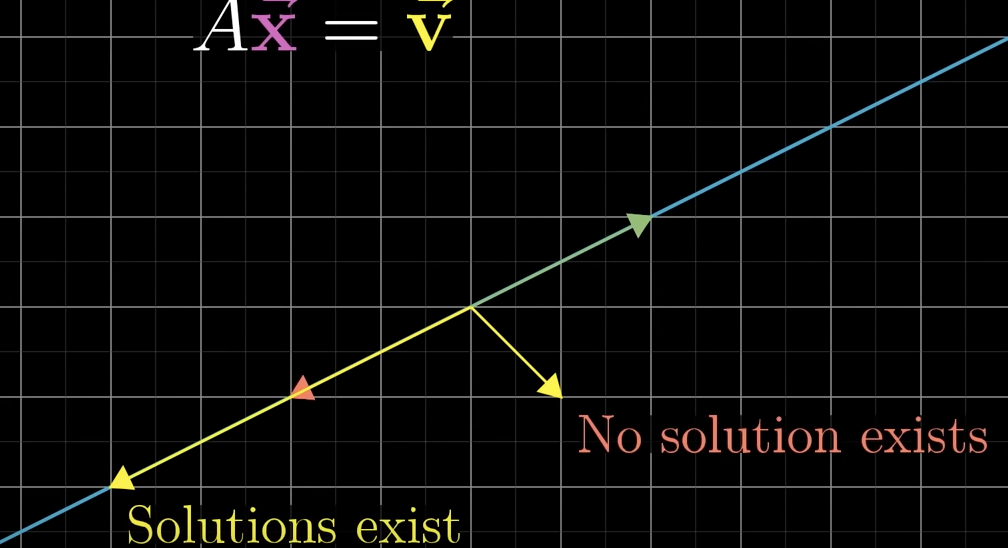
Are there still solutions even though there is no inverse?

Yes, its just that the vector has to live on the line after your transformation.

What is Rank?

Rank is how many dimensions still have volume after the transformation.

Ex)

If grid squares become parallelograms in the plane, rank = 2

If everything gets flattened into a line - rank = 1

If everything collapses to a point - rank = 0

What is the rank of a matrix?

Rank = number of independent columns = dimension of the output space that still has volume/area.

What does the outputs of your matrix mean, whether its in a place 3D or a point.

Its called the column space. Its the span of the columns of your matrix

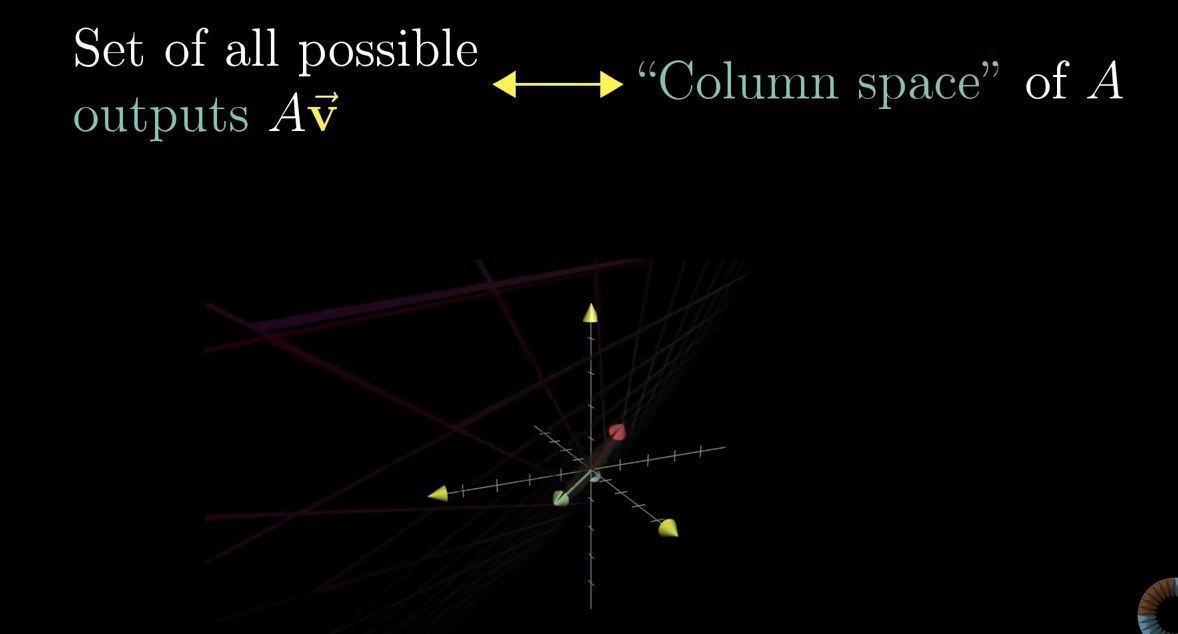
What do we call it when the rank = column space?

We call this full rank.

What is the null space?

The set of all vectors that get mapped to zero under the transfomation.

They are the vectors that go to the origin under the transformation.

What does column space help with?

See if a solution even exists.

What does null space help to do?

What the set of all possible solutions can look like.

What does inverse do?

We can use the inverse to help solve the system.

Example: If a 3×3 matrix flattens a box into a plane, what happens to the determinant, rank, and null space.

The volume becomes 0 (det=0)

One dimension is lost - rank = 2

The set of all vectors that got collapsed - null space is 1 dimensional.

Full rank vs. Low Rank

Full rank: no dimension lost - invertible

Low rank: Some dimension lost - not invertible

What is the null space again?

The set of all vectors that map to the zero vector under the matirx.

Ax = 0 - x is in Null(A)

Geometretic meaning of null space

It shows the directions that get collapsed (the dimensions that disappear).

Whats the relationship between Rank and Null Space?

rank + nullity = number of input dimensions

How should we summarize rank and null space?

Rank = what survives

Null space = what gets destroyed.

Hoe does invertibility and null space relate?

A matrix is invertible only when its null space is just the zero vector (meaning nothing gets flattened)