semantics midterm

exam on oct 23, 2025

compositionality

meaning of a part is determined by what other elements it can combine with — we can determine the meaning of the whole from the meanings of its parts

meaning as truth conditions

if we know what a sentence means, i am able to say whether it is true or false… or at least determine the conditions under which it is true

schema for truth conditions

the sentence “____” is true and only true if (iff) ____

possible worlds

possible worlds are a way of talking about alternatives

• “must”

• “might”

• “if”

partial depictions of possible worlds

proposition

meaning of a sentence — if the meaning of a sentence is its truth conditions, then the proposition expressed by a sentence amounts to its truth conditions

set theory

a set is an abstract collection of distinct objects (called members/elements) — a set is defined by its membership

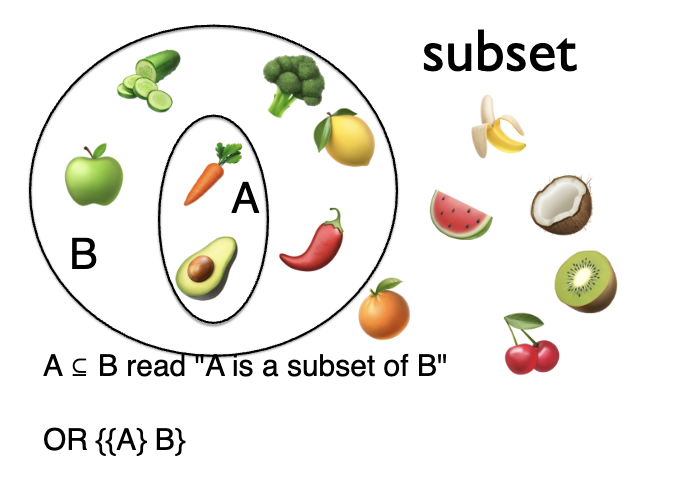
subset

A ⊆ B — A is a subset of B

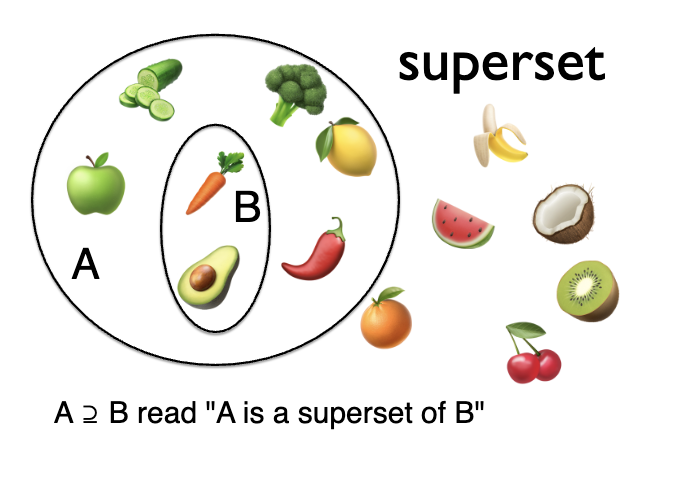
superset

A ⊇ B — A is a superset of B

relation between sets

can either hold or fail to hold

operations on sets

produce a new set from one or more sets

function

takes something as an input and gives something as an output

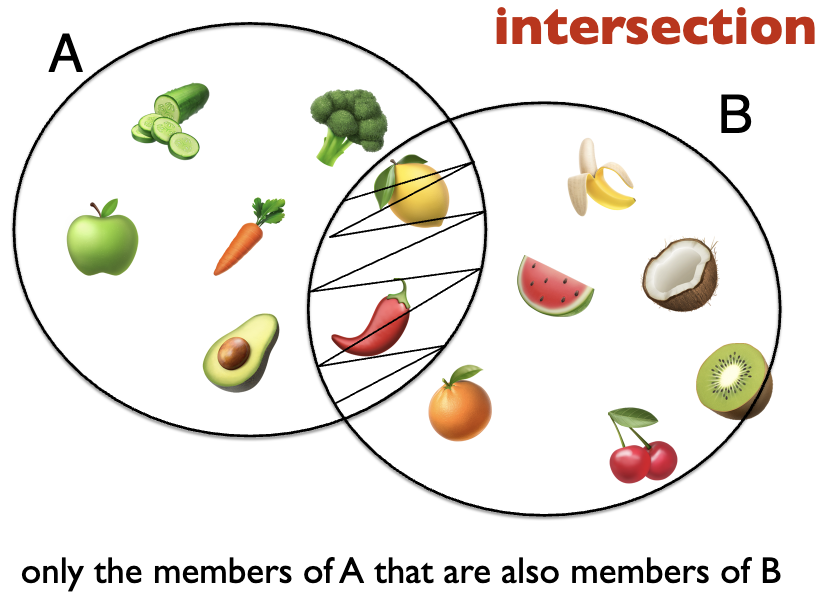
intersection

intersection of set A and set B is the function that returns the set that contains only members of A and B — C = A ∩ B

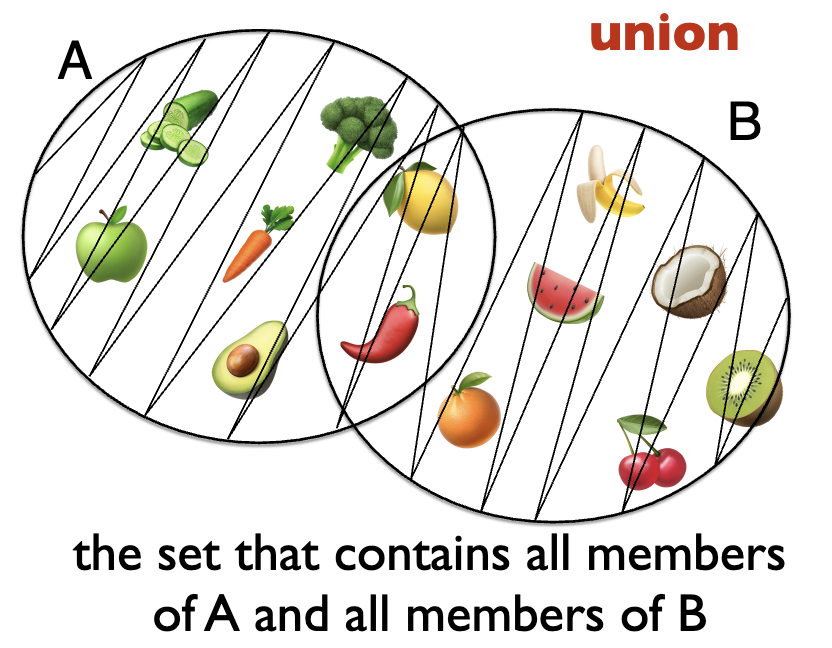
union

union of set A and set B is the function that returns the set that contains all members of A and all members of B — C = A ∪ B

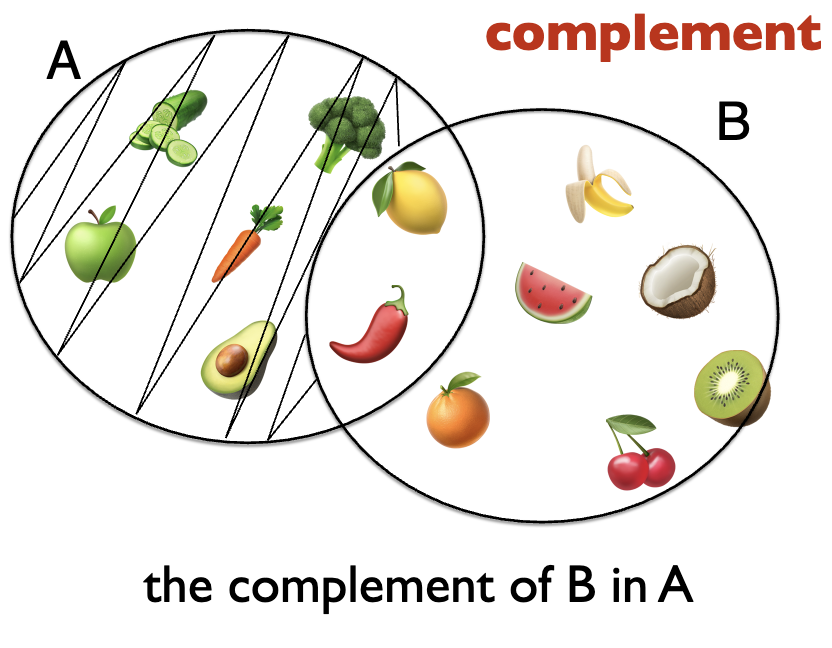
complement

complement of B in A is the set that contains only members of A and not members in set B — C = A−B

“and”

intersection

“or”

union

“either … or”

union excluding intersection

sentential negation

¬ p — it is not the case that p

• when we negate a sentence, we flip its truth conditions

• ¬ p: W − P: set of all worlds in which p is true and set of all possible worlds (W)

• the complement of P in W

p and q are synonymous

“she is taller than him” and “he is shorter than her” — P and Q are equivalent

p and q are contrary

“she is taller than him” and “he is taller than her” — the set of worlds in which p is true disjoint from the set of worlds in which q is true

• empty intersection

• p and q cannot be simultaneously true, but they could be false

contradictory propositions

if p is true, q must be false and vice versa

• “the door is closed” and “the door is open”

entailment 

p entails q if the truth of p guarantees the truth of q

• subset relationship

semantic meaning of questions

the meaning of a question is the set of its possible answers

• example: the semantic meaning of “do you have a pencil” is the set that contains the propositions “i have a pencil” and “i do not have a pencil”

semantic meaning of imperatives

an instruction as to what truth conditions are desirable to hold in the relevant world

• example: “bring a pencil!” is true and only true if in the worlds compatible with the speaker’s desires it is true that you brought a pencil

semantic meaning of exclamatives 

“what a lovely pencil!” is true and only true if in the worlds compatible with and expressing speaker’s opinions and values, it is true that it is a lovely pencil

proper names

names refer — notice that names themselves do not describe the things they refer to, they just refer

predicates

descriptive words like brown, coughs, skyscraper, and indignant have meanings about things that they describe

• predicates can be nouns, verbs, and adjectives

intension

the function determining the reference of a word/phrase — set of all possible worlds in which the sentence is true (truth conditions)

example for “the canadian prime minister”

• intension: the leader of the political party that holds the largest number of seats in the parliament

extension

the value of that function — truth values, true or false 

example for “the canadian prime minister"

• extension: mark carney

saturation

utterances are composed from saturated and unsaturated parts

predication is saturation

“___ swims”

• is true only if after we fill the gap with a referent, we get something that is true

• we know what we need to fill in to get a complete, saturated proposition

• predicates are semantically incomplete in isolation — needs entities

type- driven approach

part of the meaning of unsaturated propositions is that we know what they need to be combined with

types

• e: entity/individual

• t: truth values

<e,t>

anything that needs to combine with a referent (entity/individual) to return a truth value — predicate/property

intransitive predicate

<e,t>

transitive predicate

<e,<e,t>>

ditranstive predicate

<e,<e<e,t>>>

semantically vacuous words

• be

• “a(n)” when combined with “be”

modification as saturation

<<e,t>,<e,t>>

modification as intersection

<e,t>

predicative adjective

predicates that require saturation

• “that student is asleep"

attributive adjectives

noun-modifying adjectives — adjuncts 

adverbs

<e,t>

“the”

<<e,t>,e>>

• takes a property (a set of individuals for which the property is true), and returns exactly one of the individuals from the set

• “old” — previously mentioned/shared/common ground

• the most salient and unique

“a(n)”

<<e,t>,e>>

• takes a property (a set of individuals for which the property is true), and returns exactly one of the individuals from the set

• new, not currently present in the common ground