normal distribution & 68-95-99,7 rule

normal distribution & 68-95-99,7 rule

Parameter

a number that describes the data from a population

Statistics

a number that describes data from a sample

Parameter

a number that describes the data from a population

Statistics

a number that describes data from a sample

Sample (mean & standard deviation) signs

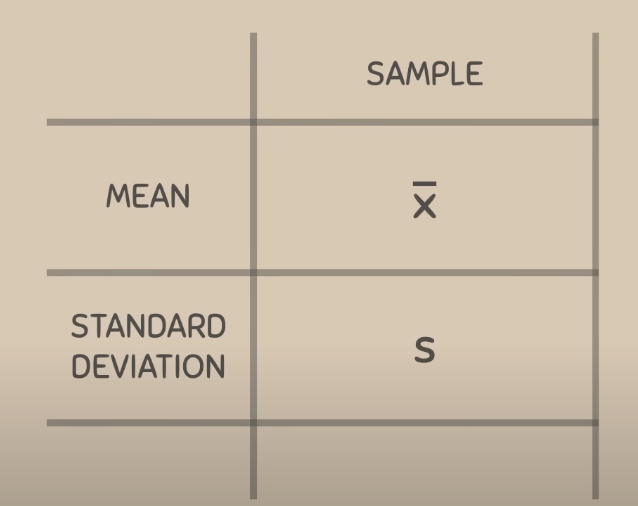
these are statistics

population (mean & standard deviation) signs

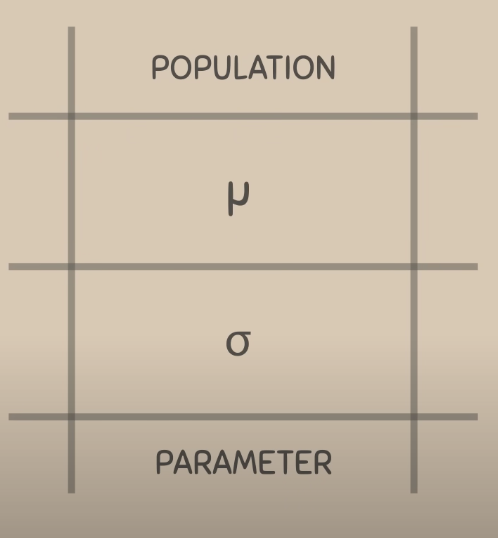
these are parameters

• important when we talk about normally distributed populations

Normal distribution

• a special type of density curve which is bell shaped

what does the normal distribution describe

• the tendency for data to cluster around a central value, which is the mean

• the mean is always located in the middle or central (mu is the mean in a population distribution, and x-bar is the mean in a sample distribution)

how we describe a normal distribution

• some data values fall below the mean

  

• some data values fall above the mean

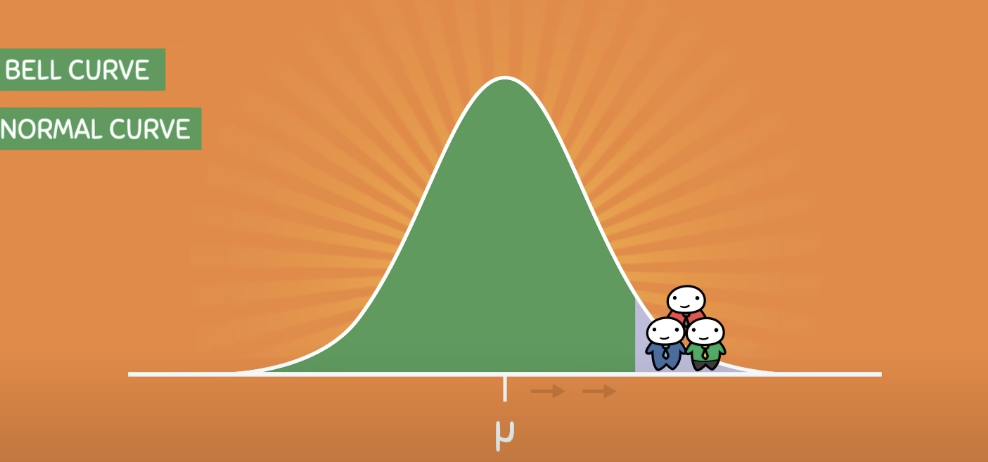
• but most of the data values are located near the mean

  

in normal distribution

• characterizes the position of the normal distribution

• if we increase the mean, the curve will follow & move towards the right

• if we decrease the mean, the curve will follow & move towards the left

  • this happens because the data will always cluster around the mean in normally distributed populations, thus the value of the mean determines the position of the normal distribution.

in normal distribution

• sigma characterizes the spread of the normal distribution

• the larger the standard deviation the more spread out the distribution will be

• the smaller the standard deviation the less spread out the distribution will be

when the spread increases

• the curve gets much flatter

when the spread decrease

the spread gets much taller

what is the reason for that the curve gets flatter or taller when data increase or decrease

• the normal distribution is a density curve, & the total area of any density curve must remain equal to 1 or 100% = thus the changes in the width of the curve must be compensated by changes in the height of the curve

The normal distribution is unimodal

• meaning that the normal distribution has a single peak

the normal curve is symmetric about its mean

• meaning that the distribution can be cut into two equal halves

the parameters mu and the sigma completely characterizie the normal distribution

• meaning that the population mean mu determines the location of the distribution and where the data clusters around the population standard deviation sigma determines how spread out the distribution will be

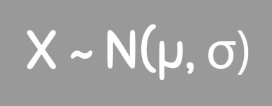
• the notation given to a population that follows a normal distribution

• for the variable X, it follow a normal distribution and has the mean mu with a standard deviation of sigma

68-95-99,7 rule

• in a distribution we first need to create the intervals that increase by the standard deviation (sigma in population/ s in sample)

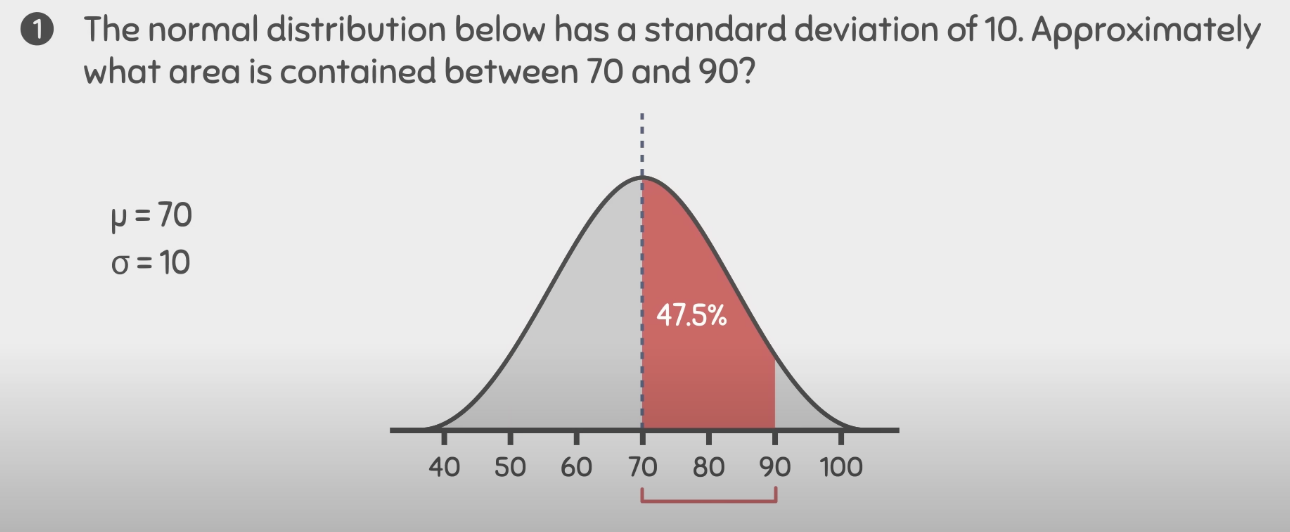
• within one standard deviation away from the mean, the total area contains of 0.68 or 68%

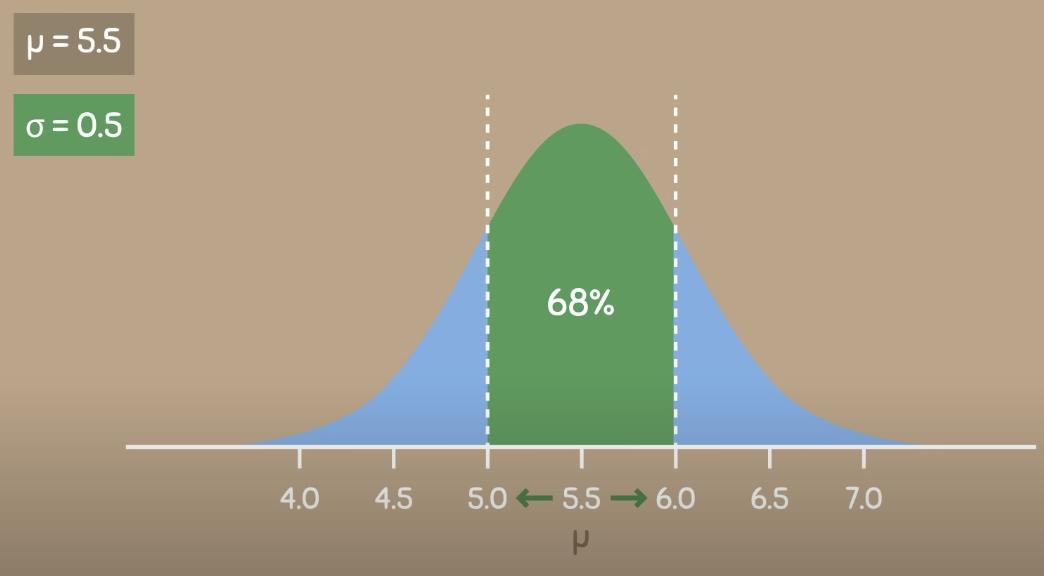
• we can say that 68% of the population have a height between 5.0 & 6.0 feat

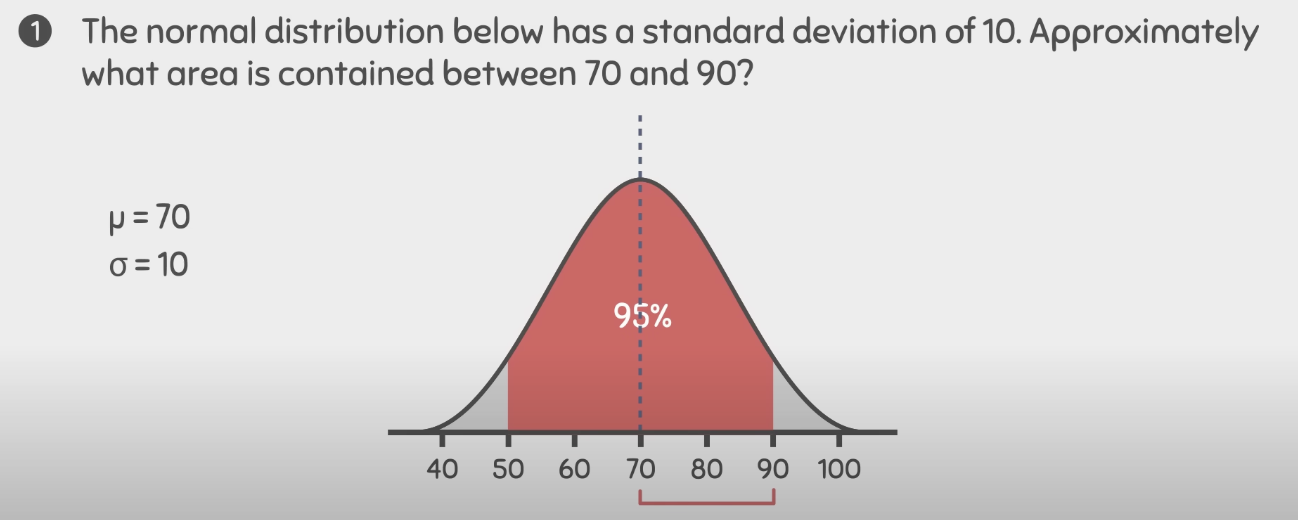
• within two standard deviations away from the mean, the total area contains of 0.95 or 95%

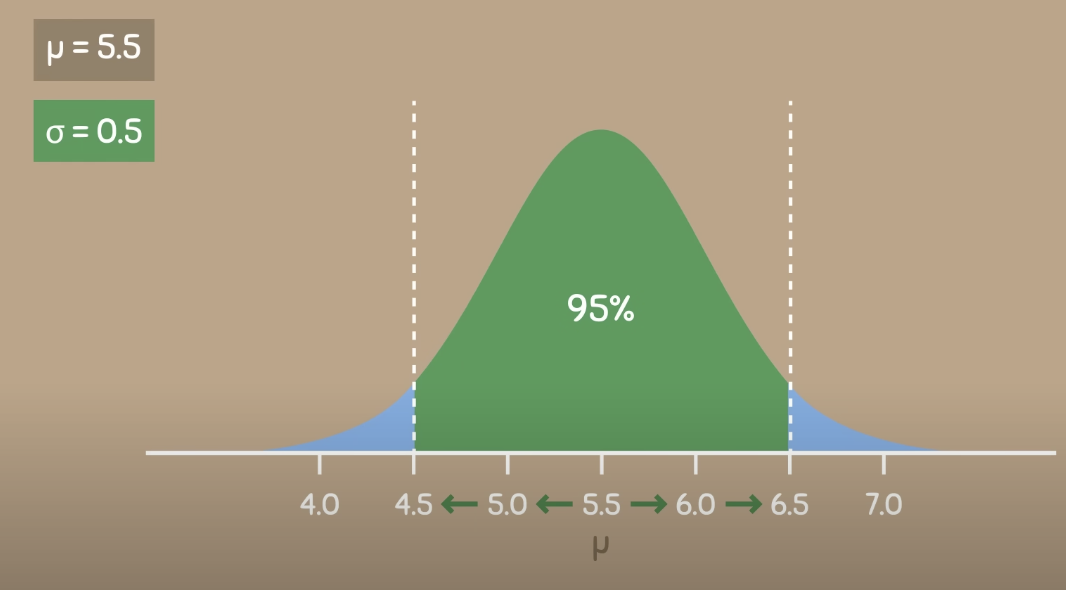
• This means that 95% of the people in the population have a height between 4.5 & 6.5 feat

• within three standard deviations away from the mean it contains a total area of 99,7%

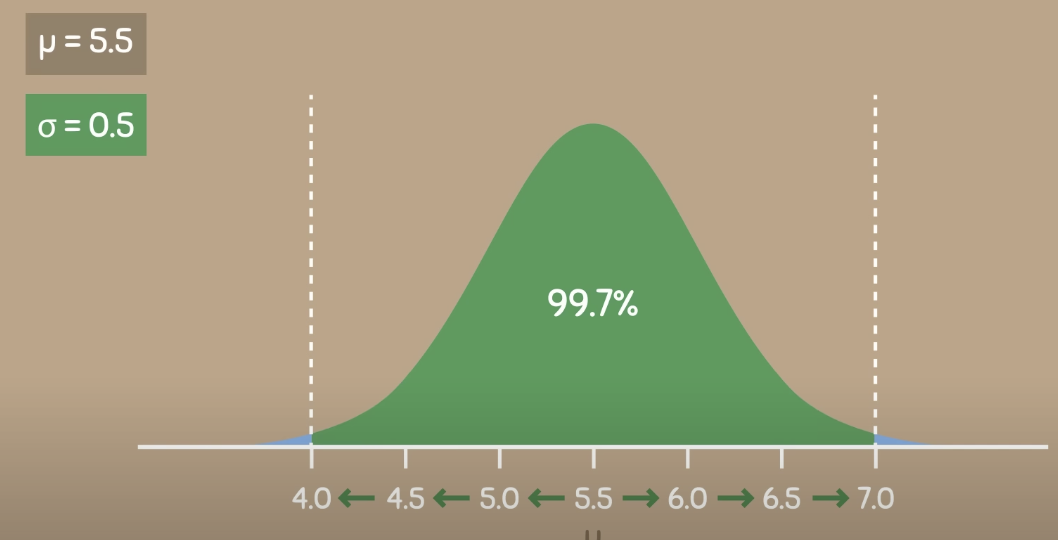
• we can say that 99,7% of the people in a population have the height between 4.0 and 7.0.

What happens if we go four or six standard deviations from the mean?

• since a normal distribution never touches the x-axis, you can go to the infinity, but the distribution will be very small