Academic Team Math

The ultimate flashcard study set for the KAAC Governor's Cup Academic Team high school mathematics competitions. Regularly updated and fully comprehensive

a=b b=a

symmetric property

consistent

a system of equations with at least 1 solution

(x-h)^2=4p(y-k)

focus and directrix parabolic standard form (focus and directrix are p away from vertex (h,k))

cos^2x-sin^2x

2cos^2x-1

1-2sin^2x

cosine double angle identity

4p

latus rectum of parabola formula (perpendicular line to major/transverse axis crossing through foci)

2pi*sqrt((a^2+b^2)/2)

perimeter of ellipse

geometric mean theorem

in a right triangle, the altitude divides the hypotenuse into two segments. the length of the altitude is the geometric mean of the lengths of the two segments because the triangles are similar.

nilpotent

equal to zero when raised to some power. (all eigenvalues are 0)

eigenvalue

A scalar λ such that after finding A-λI and taking its determinant, set equal to 0 and solve for λ

parallelepiped

A solid body of which each face is a parallelogram. Also known as "cubes" or "prisms". In R3. volume is found using determinant of matrix with side vectors as vertical basis vectors of transformation matrix

1/2pl+b

surface area of pyramid (p=perimeter of base, l=slant height, b=base area)

2^n-1

number of proper subsets in a set

gabriels horn

AKA Torricelli's trumpet. type of geometric figure that has infinite surface area but finite volume.

standard deviation/sqrt(n)

standard error of mean (SEM) formula

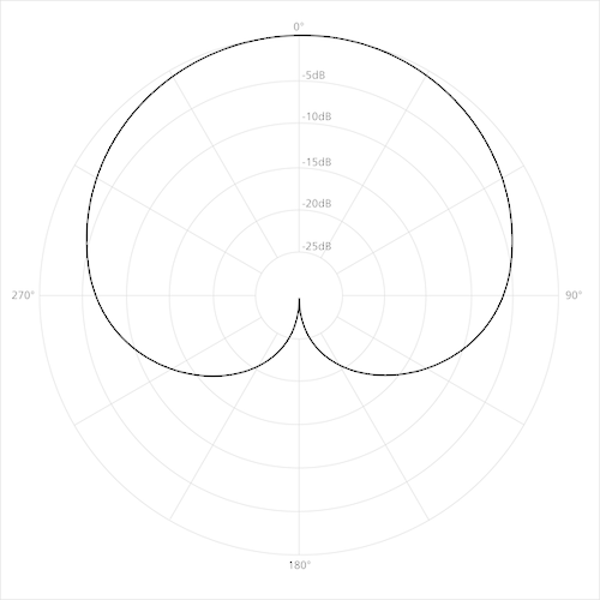
cardioid

(r=a±asinθ, r=a±acosθ). what is the name of this polar graph

abelian group

A group that is commutative. if every element is its own inverse, it is one of these, but that is not the only way to be this.

oblong number

a whole number that has a geometric representation in the shape of the rectangle, where the length and width differ by exactly one unit

nth of one these numbers = n(n-1)

transcendental function

A function that cannot be expressed in terms of algebraic operations, such as an exponential or logarithmic function.

collatz conjecture

All positive integer will become 1 by repeating: if even, divide by 2; if odd, multiply by 3 and add 1

3n+1

n/2

brahmaguptas formula

for cyclic quadrilaterals, area=√(s-a)(s-b)(s-c)(s-d) where s is semiperimeter. extension of herons formula. a cyclic quadrilateral is a quadrilateral inscribed in a circle

fixed point

a point in a function where the input equal the output: f(z)=z

fermats last theorem

this unsolved theorem states that there are no three positive integers a, b, and c such that a^n+b^n=c^n for any integer value of n greater than 2.

wrapping function

the function that maps points on a real number line to points on the unit circle. f(s)=s radians around the unit circle

oblique asymptote

for a rational function, if numerator degree is 1 higher than denominator degree, oblique asymptote line is result of polynomial division

derangement

permutation of a set where no item is in its original position. denoted !n.

formula: floor of (n!/e + 1/2)

actualization

the process of assigning specific values to a variable. AKA realization

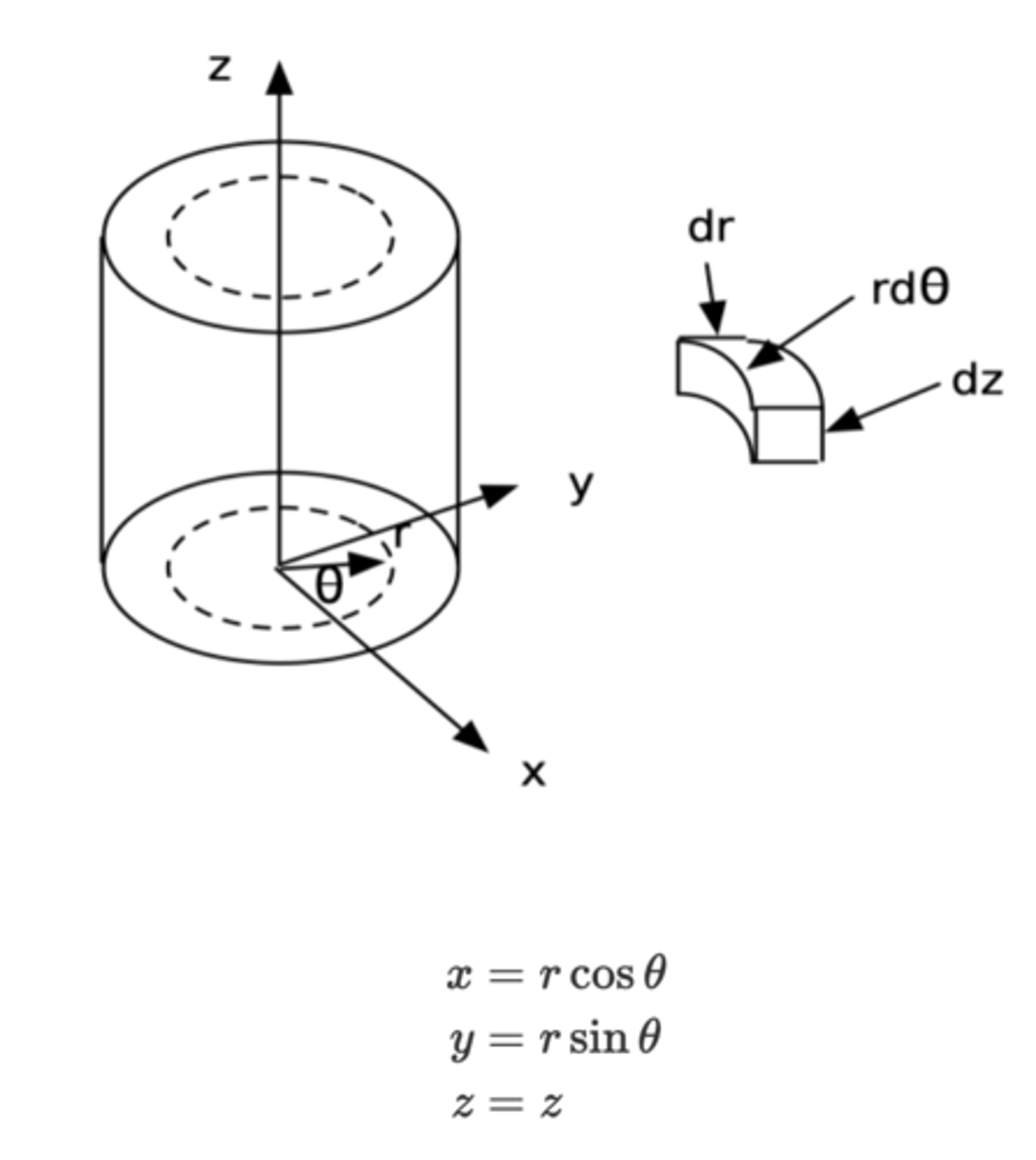
cylindrical polar coordinates

these polar coordinates are denoted (r,θ,z), where:

r is the radial distance from the origin to the point in the xy-plane.

θ is the polar angle, measured counterclockwise from the positive x-axis to the line connecting the origin to the point.

z is the vertical coordinate, representing the height above or below the xy-plane.

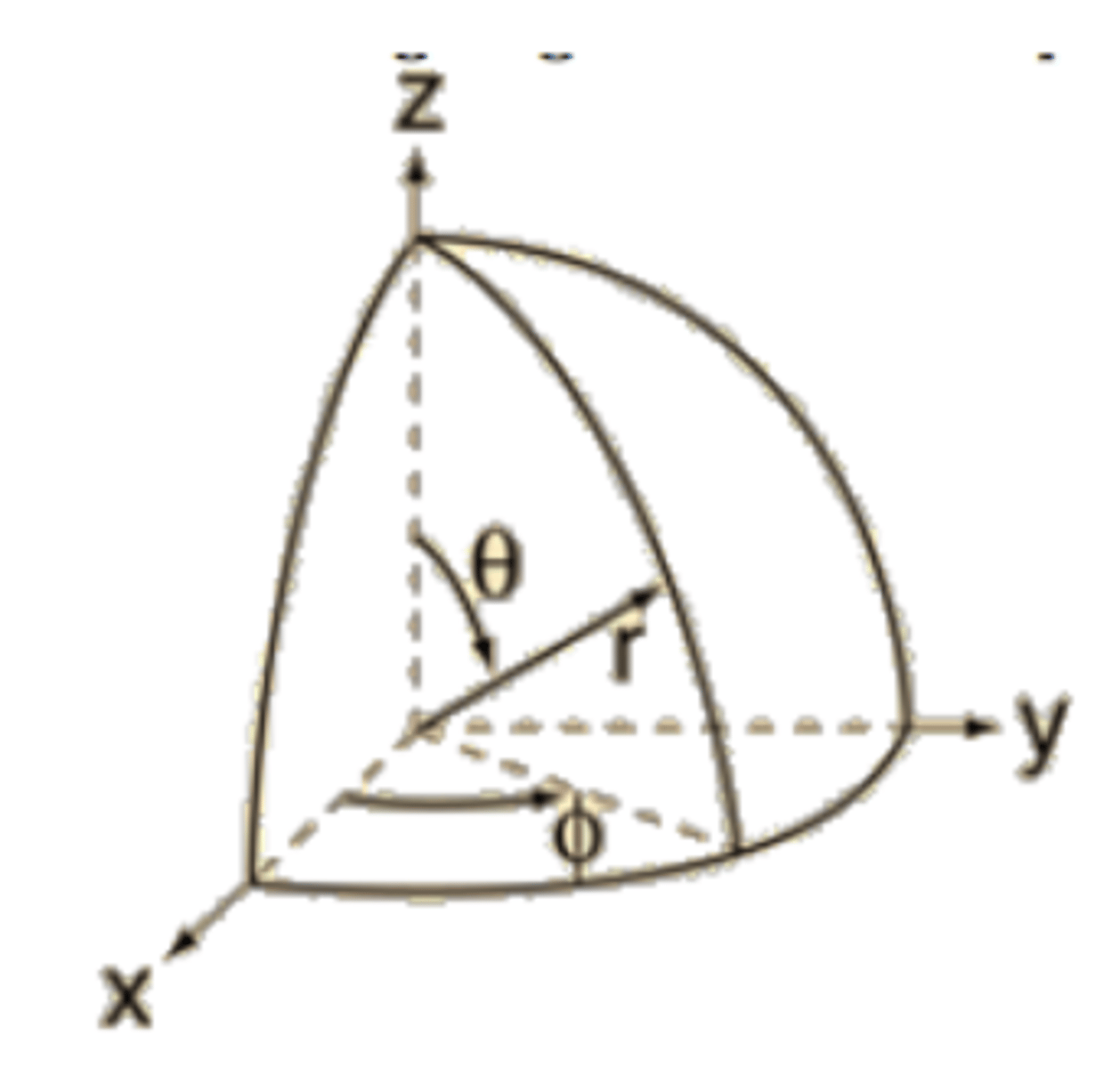
spherical polar coordinates

these polar coordinates are denoted as (r,θ,ϕ), where:

r is the radial distance from the origin to the point.

θ is the polar angle, measured counterclockwise from the positive x-axis in the xy-plane.

ϕ is the azimuthal angle, measured from the positive z-axis to the line connecting the origin to the point.

polar derivative

same as using product rule on top and bottom of:

rsintheta/rcostheta

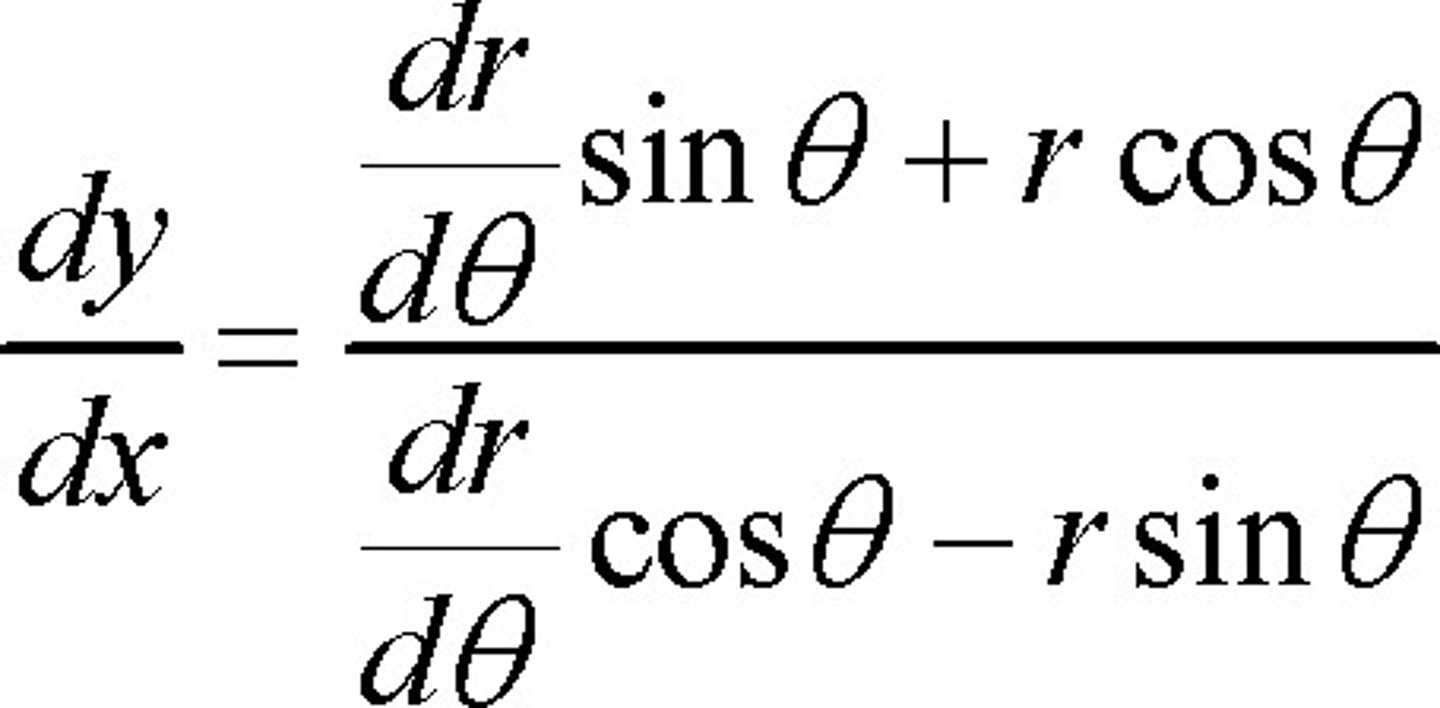
polar integral

1/2 * integral of r^2 dtheta

cantor

this german mathematician formulated set theory

hausdorff

this mathematician introduced fractional dimensions and defined topology

isometry

A transformation that does not change the size or shape of a figure.

surface area of function

double integral over the region D of sqrt(1 + (partial derivative w.r.t. x) ^2 + (partial derivative w.r.t. y) ^2)

divergence formula

add up components of gradient vector

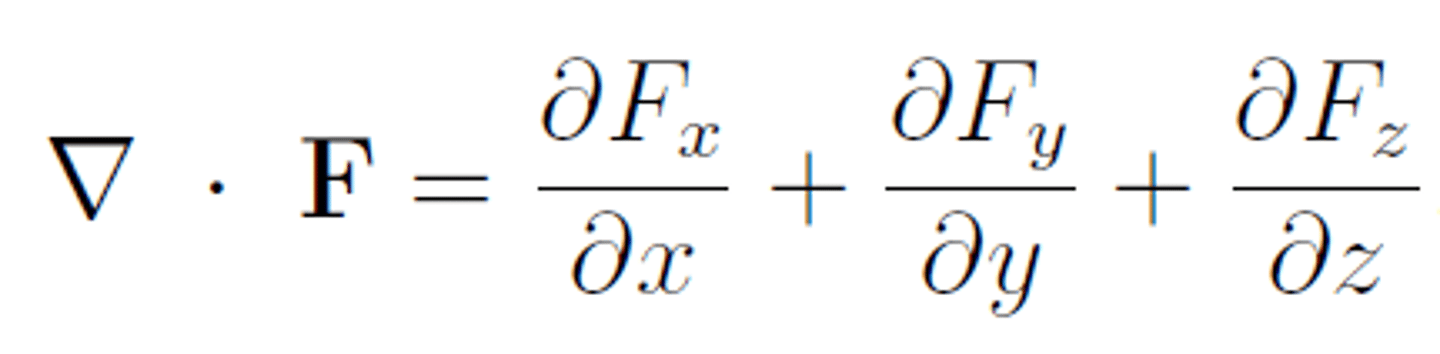
bayes theorem

this theorem defines the probability of an event occurring based upon other event probabilities.

P(A|B) = P(A∩B)/P(B) = P(B|A)P(A)/P(B)

example: P(rolling an 2 given even number) = P(rolling an even 2) / P(even number)

n(n-3)/2

number of diagonals of a polygon formula

n(a+l)/2

arithmetic series partial sum

a1(1-r^n)/1-r

geometric series partial sum

a1/1-r

geometric series infinite sum (-1 < r < 1)

nCkp^k(1-p)^(n-k)

binomial distribution (probability of k successes in n trials)

1/p

geometric distribution (expected number of trials until a success)

a=a

reflexive property

c^2=a^2+b^2-2abcosC

law of cosines

sinA/a=sinB/b=sinC/c

law of sines

1/2absinC

law of sines area formula

sqrt(s(s-a)(s-b)(s-c))

herons formula (s=(a+b+c)/3)

centroid

average of vertex points of triangle. intersection points of medians of triangle (lines from each vertex to opposite midpoint)

1/2ap

area of regular polygon

n!/duplicate letters!

number of unique permutations of a word of length n

least squares regression

the slope of this regression line is the square of the values

correlation coefficient

this value is r in least squares regression. AKA pearson coefficient

coefficient of determination

this value is r^2 in least squares regression.

F+V-E=2

eulers formula

cross product

vector orthogonal to 2 other vectors A, B. (dot products are 0). find determinant of following 3×3 matrix:

[ i j k ]

[ a1 a2 a3 ]

[ b1 b2 b3 ]

determinant: multiply each of top row values by determinant of 2×2 matrix outside row and column and subtract middle term (j)

magnitude: |A||B|sintheta

area of triangle created by 2 vectors = ½ of the magnitude of the cross product of the vectors.

inconsistent

a system of equations with no solution

independent

a system of equations with exactly 1 solution

dependent

a system of equations with infinite solutions

rational roots theorem

for a standard polynomial with integer coefficients, the possible roots are form p/q, where p = all factors of last, constant term and q = all factors of leading coefficient. factors can be both positive and negative

descartes rule of signs

for a standard polynomial, the number of positive roots = all numbers that are equal to or less than (by a multiple of 2) the number of sign changes. must be in descending order.

(x,y) -> (y,x)

reflection across y=x

2sinxcosx

sine double angle identity

ellipse

x^2/a^2 + y^2/b^2 = 1

a=length of semi major axis

b=length of semi minor axis

a^2-b^2=c^2

foci are c away from center on major axis

parametric form:

x = h + a cos t

y = k + b sin t

2b^2/a

latus rectum of conic sections (besides parabola) formula (perpendicular line to major/transverse axis crossing through foci)

0, c/a, 1, c/a

give formulas for eccentricity of conic sections in order:

• circle

• ellipse (0 < e < 1)

• parabola

• hyperbola (1 < e)

hyperbola

x^2/a^2 - y^2/b^2 = 1

a=length of semi transverse axis (the main one)

b=length of semi conjugate axis (the perpendicular one)

vertices are at (a, y), (-a, y) or (x, a), (x, -a)

a^2+b^2=c^2

foci are c away from center on transverse axis

y=bx/a, y=-bx/a

asymptotes of hyperbola. THE Y ALWAYS HAS THE B

1.5*IQR

interquartile rule (finds limit for outliers)

taylor series

polynomial with infinite number of terms to approximate behavior of function at a given point

g(x)=sum of f^(n)(a)(x-a)^n/n! from n starting at 0

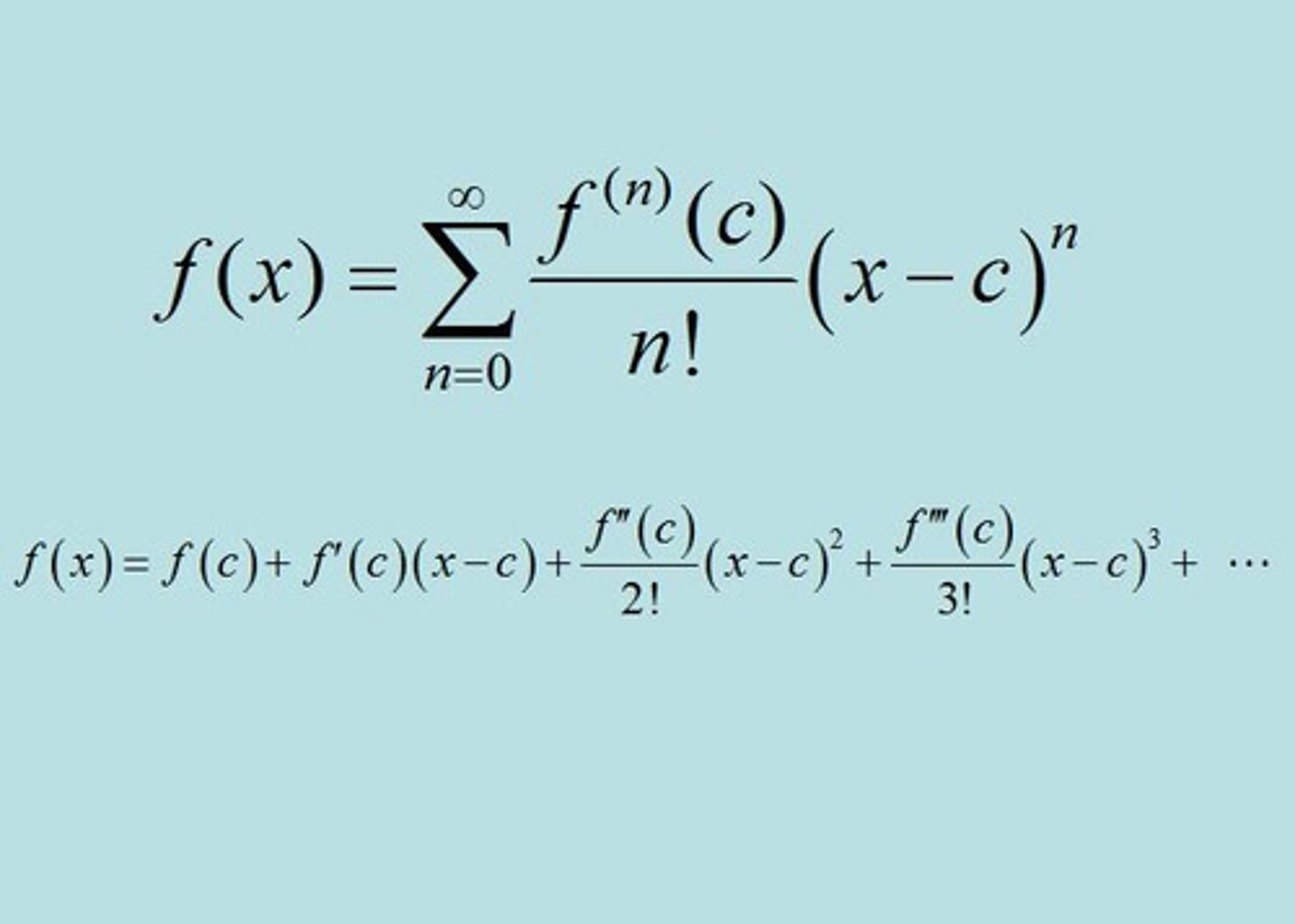
2^n

number of subsets in a set

de morgans law

laws in Boolean algebra which state that the complement of the intersection is the union of the complements. !(A && B) = !A || !B distribute not flip and/or

de moivres theorem

If z= [r(cos theta + i sin theta)], then z^n=(r^n) (cos ntheta + isin n*theta).

remainder theorem

if a polynomial f(x) is divided by x-k, the remainder is r=f(k)

fubinis theorem

this theorem converts double integrals to iterated integrals for easier evaluation, especially on rectangular regions of R. this allows the inner integral to be evaluated first, treating the other variable as a constant, before doing the outer integral.

gradient

the multivariable generalization of derivatives. in n dimensions, it is an n-1 dimensional vector where the kth term is the partial derivative of f(x) with respect to the kth variable

directional derivatives

the instantaneous rate of change of a function as the input (x,y) changes along a velocity vector v. equal to dot product of gradient and velocity vector

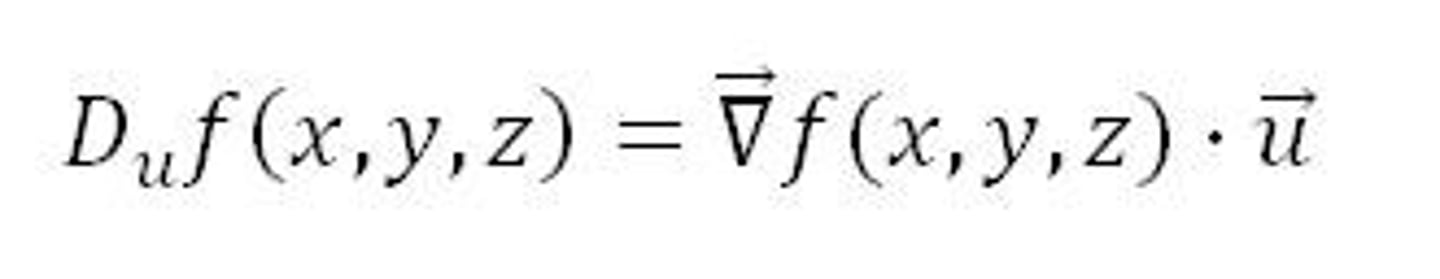
chebyshevs rule

for any number k >= 1, at least 100(1-1/k²)% of the observations in any data set are within k standard deviations of the mean

simpsons paradox

when averages are taken across different groups, they can appear to contradict the overall averages

game theory

the study of how people behave in strategic group situations. developed by John von Neumann and Oskar Morgenstern

calculator tricks

• cdf: cumulative density function (range)

• pdf: probability density function (single value

• invNorm: converts left cdf to interval. endpoints can then be used to find z score

• invT: converts left cdf and DOF to z score critical value. use for unknown std. dev. or n < 30

• numeric solver at bottom of math solves equations

Prop - proportion

Samp - sample

Z - known standard deviation or n > 30

T - unknown standard deviation or n < 30

Int - interval

• 1/2-PropZTest: hypothesis test about proportions

• 1-PropZInt: confidence interval of proportion. if trying to find min n for max MOE, use this with x = 0.5*each n

• 2-SampZTest: compare means of 2 samples

• 2-SampTTest: compare means of 2 samples with unknown standard deviation

• 2-SampFTest: compare variances of 2 samples

• rref: solve system of equations from augmented matrix

• list → seq to get sequence of values from explicit formula

• store value in x and spam a recursive formula that stores successive values in x to solve for the nth term of a recursive sequence.

• inverse reciprocal trig functions are equal to the inverse of the normal trig function applied on 1/x. ex. sec^-1(x)=cos^-1(1/x)

• cosh, sinh, and tanh functions are in catalog. press a letter to go to the function for that letter. dayOfTheWeek for a given date is also in catalog

• go to catalog and run DiagnosticOn to get r and r² statistics displayed during regression

• angle submenu allows conversion to DMS (degrees minutes seconds).

• draw menu → draw circle, inverse function, tangent

degenerate circle

circle with radius 0

mandelbrot

this polish mathematician first coined the term fractal

dual of a polyhedron

the vertices of this correspond to the faces of the original.

power of significance test

probability that a significance test will correctly identify a positive effect.

= 1 - probability of false negative (type II error)

moments

in statistics, they are quantities representing non-locational expected values of a distribution. 1st, 2nd, etc.

• 0th: sum of distribution

• 1st: mean of distribution

• 2nd: variance of distribution

• 3rd: skewness of tails: if 0, balanced, if positive, longer right tail (right skew), if negative, longer left tail (left skew)

• 4th: kurtosis: combined weight of tails relative to distribution

geometric distribution

this distribution models the probability of doing something until a desired outcome has been achieved. eg. rolling a dice until you get 6.

• expected value/mean: 1/p

• expected value/mean if including 0: (1-p)/p

• variance: (1-p)/p²

calculating least squares regression line

y=mx+b

m=( σy / σx )*r

b=mean - m*mean

test statistic

number from a statistical test, used to find if your data could have occurred under the null hypothesis

two types:

• T test: compare means for (n < 30). normally distributed data with unknown σ. T-Test on calculator

• Z Test: compare means for (n > 30). normally distributed data with known σ. Z-Test on calculator

circumscribed circle formula

the DIAMETER of this circle = the common ratio of a/sinA=b/sinB=c/sinC or the RADIUS of the circle = abc/4*area of triangle using herons formula

inscribed circle formula

the RADIUS of the circle = herons formula but divide s instead of multiply:

sqrt(((s-a)(s-b)(s-c)/s)

a-b/a+b=tan 1/2(A-B)/tan 1/2(A+B)

law of tangents formula

statistics symbols

	population	sample
size	N	n
mean	µ	x bar
standard dev.	σ	s
correlation coefficient	p	r
proportion	p	p̂

x^n/n!

power series of e^x from n=0 to infinity

power series

series containing x as well as n. Convergence of series is determined by x value. always converges for x=a

form: ∑c_n(x−a)^n where c_n is a subseries

radius of convergence (R): there is R such that the series converges for |x-a|<R

interval of convergence: interval of all xs of convergence. based on R. may or may not include endpoints (they must be tested separately).

how to find: use ratio test and factor out |x-a|. this limit must be < 1 to converge based on the test. solve to put in R form.

Pe^rt

formula for CONTINUOUS compound interest. P=principle, r=rate from 0 to 1, t=time in years

half angle formulas

platonic solids

tetrahedron: 4 sides, equilateral triangles, triangular pyramid

cube: 6 sides, squares

octahedron: 8 sides, equilateral triangles, two pyramids stacked

dodecahedron: 12 sides, 30 edges, 20 verts, pentagons

icosahedron: 20 sides, 30 edges, 12 verts, equilateral triangles

how to derive num edges:

• multiply num faces by num sides

• divide by 2 to get rid of overcounting (since edges are shared by 2 faces)

how to derive num vertices:

• multiply num faces by num sides

• find max num of faces that that intersect a single vertex. since we arent in 2D plane, it will be less than the max in the 2d plane.

cos(x)cos(y)-sin(x)sin(y)

cos(x+y)=

sin(x)cos(y)+cos(x)sin(y)

sin(x+y)=

how to derive sum and difference identities

1. use euler’s identity: e^itheta=costheta+isintheta

2. plug in x+-y as theta to get one side of equation

3. use exponent rules to rewrite as product of 2 separate exponentials and expand them into trig form

4. equate both sides

5. equate real and imaginary parts

6. solve for cos(x+-y) or sin(x+-y)