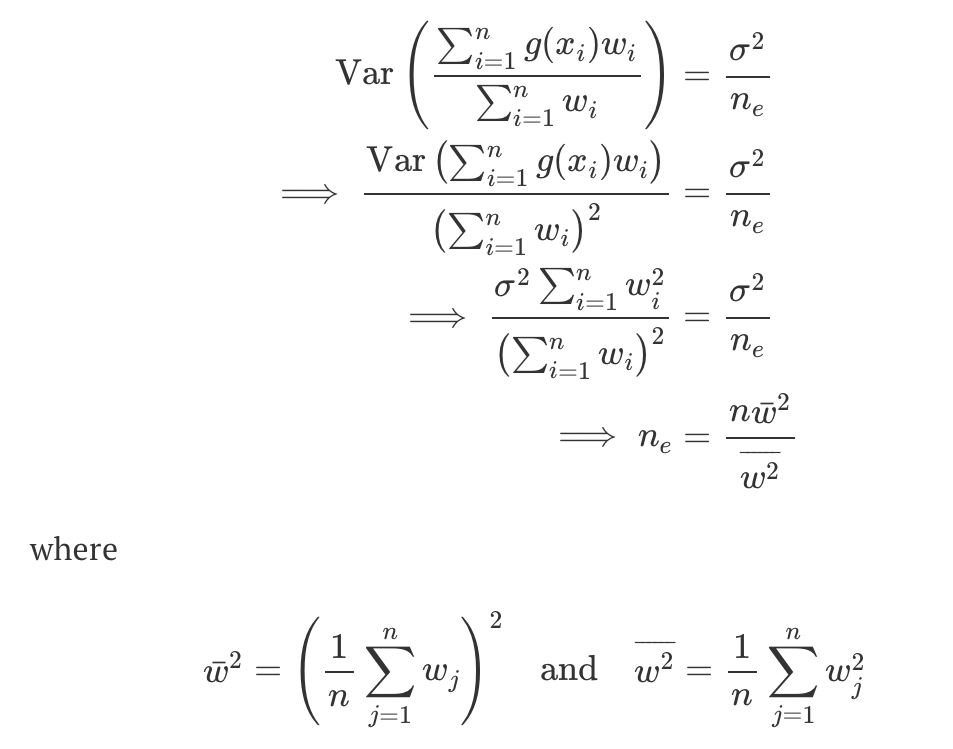data science and statistical computing

unbiased estimate of the population standard deviation

estimate of the standard deviation of the sample mean

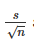
a t-distributed variable

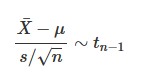
one sided p-value

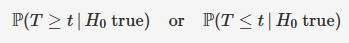
two sided p-value

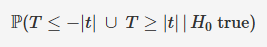
monte-carlo testing

given data (x1,…,xn), an observed test statistic t = h(x1,….,xn), a data generating distribution F(x|theta) and a hypothesis as below, give the steps to perform a monte carlo hypothesis test.

(known s.d. but not unknown)

simply putting the process of hypothesis testing

bootstrap estimate and standard error

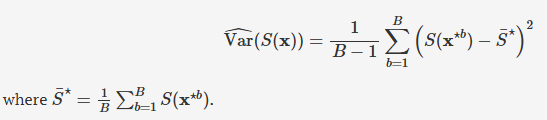
cdf (or just distribution function)

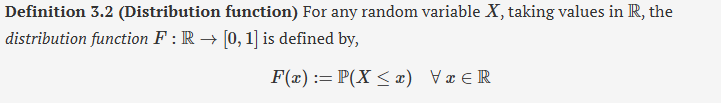
empirical cdf (or empirical distribution function)

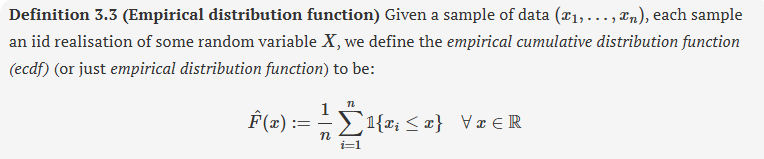
conditions for a valid cdf

Glivenko-Cantelli theorem

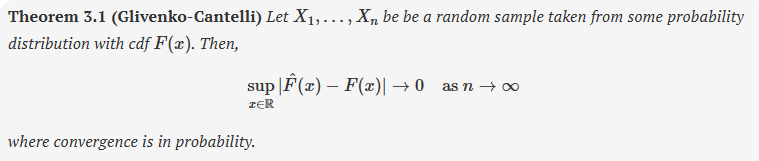
lemme 3.1 - sampling uniformly at random is equivalent to…

ecdf approximates…

the true cdf

bootstrap resampling is equivalent to…

sampling n times from the ecdf (with replacement)

bootstrap is equivalent to first fitting an ecdf to the data and then…

sampling from it as though this was a fitted distribution

probability mass function when assigning probability 1/n at each value xi (for discrete random variable)

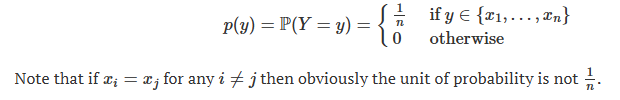
E[Y]

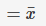
Var[Y]

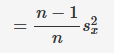
look at the mean of a sample of m draws from an ecdf constructed on n data points, and give the expectation and variance of the mean:

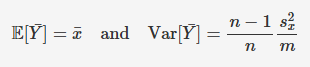
bootstrap standard error for the mean

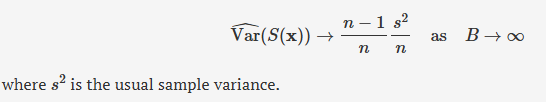
special cases in which the standard bootstrap procedure needs more care

what value of f = n/N indicates that the effect of the finite population size cannot be dismissed

0.1

theorem 3.2 - finite population variance of the mean

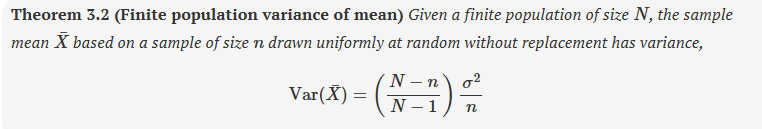
important notes about the finite population variance of the mean

theorem 3.3 - unbiased estimator of Var(Xbar)

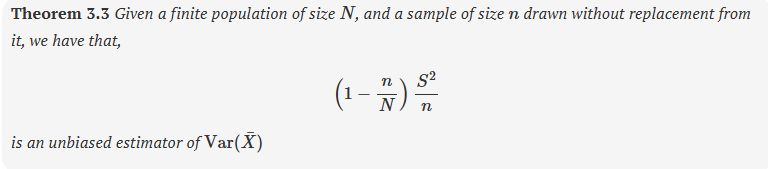
altering the finite case so that it works

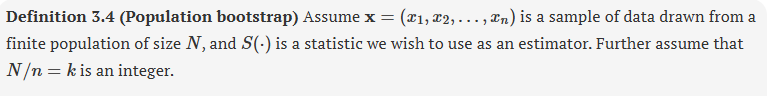
population bootstrap

parametric bootstrap estimate and standard error

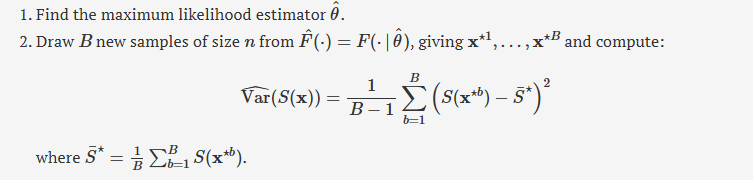
using bootstrap samples

bias from stats I

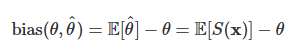
basic bootstrap bias estimate

bias correction

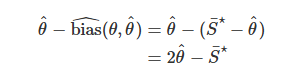
100(1-a)% confidence interval using the bootstrap estimate of standard error

where za/2 is the 100(a/2)% percentile of that standard normal distribution

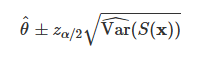
100(1-a)% confidence interval

probability of the sampled coordinates being inside the circle

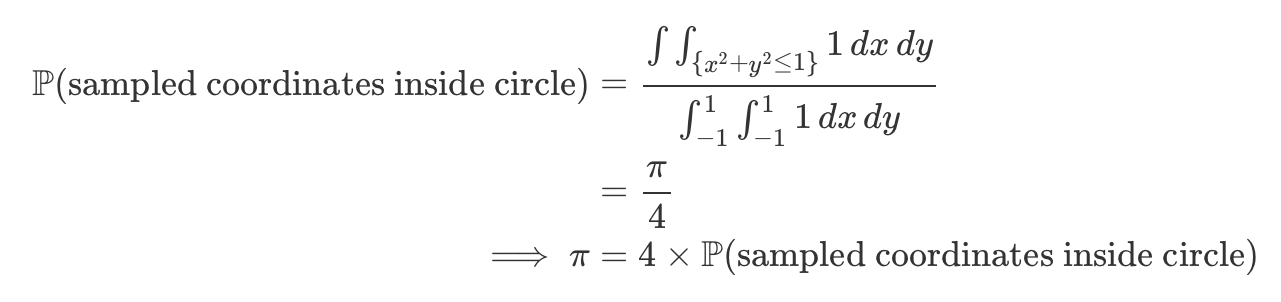
mu as an integral

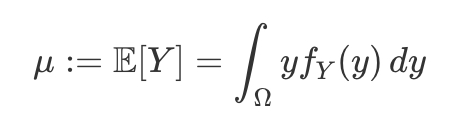
approximating mu (as a sum)

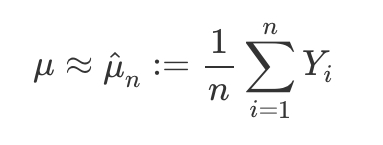
weak law of large numbers

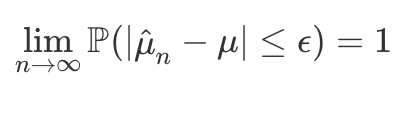
expressing mu as an integral with Y=g(X)

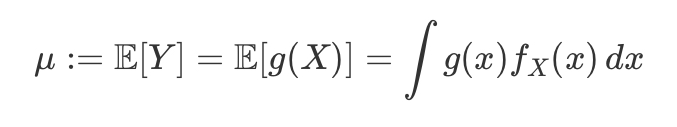
X ~ Unif(a,b) pdf

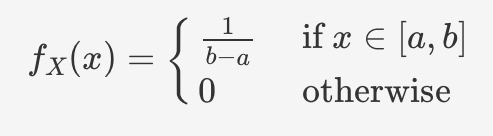
when Var(Y) = σ² < inf, then give the expectation of μ^n

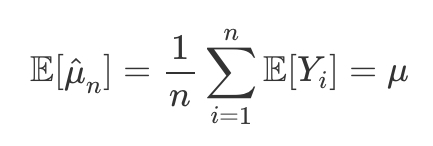
Var(μ^n)

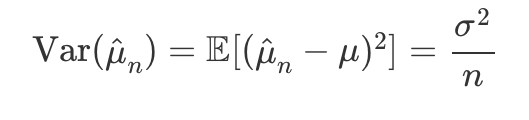
mean squared error (MSE) and root mean squared error (RMSE)

orders f functions

Riemann integral

using Chebyshev’s inequality to provide a probabilistic bound on the absolute error exceeding a desired tolerance

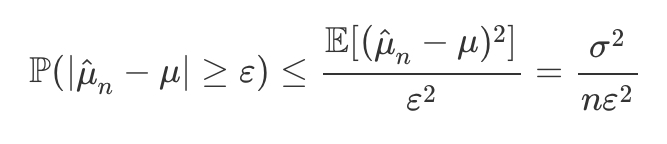
CLT

confidence interval where g(.) is some constant multiple of an indicator function

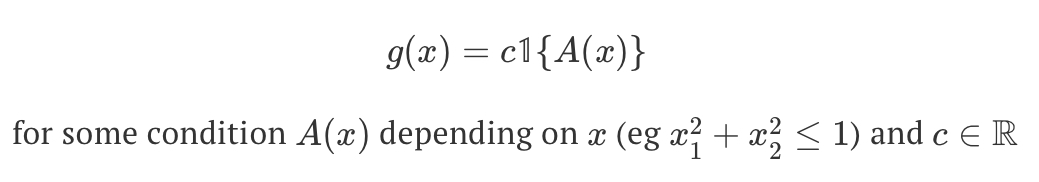
p^n

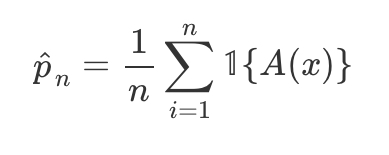
binomial confidence interval

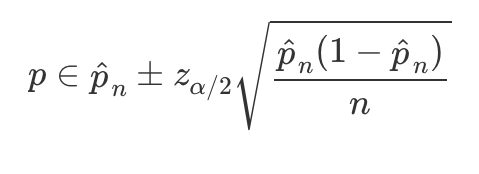
overall integral for mu

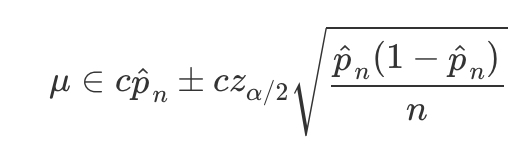
probability inequality

relative error at most δ

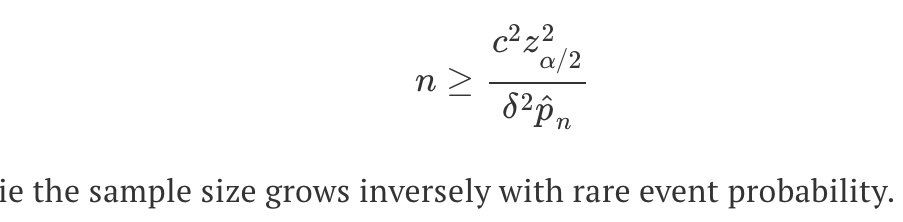
Bayesian posterior and its expectations

statement of probability computable as expectations

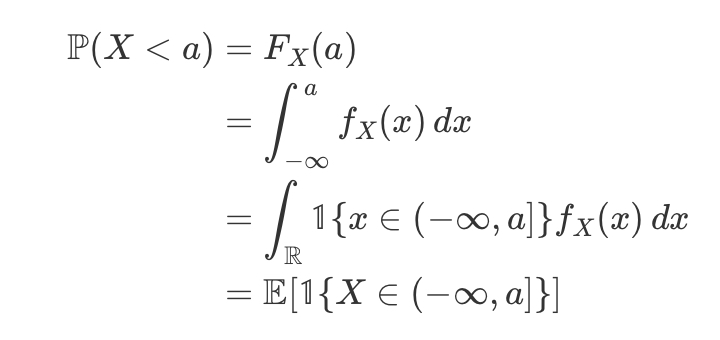
inverse transform sampling

generalised inverse cdf

theorem 5.1 - generalised inverse cdf

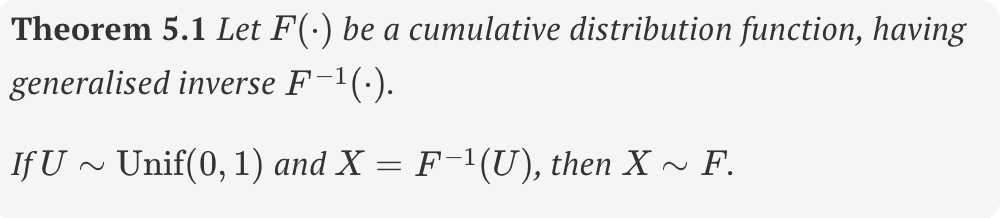
rejection sampling

lemma 5.1 - when proposal an target are normalised pdfs…

theorem 5.2 - generating X

mu (importance sampling)

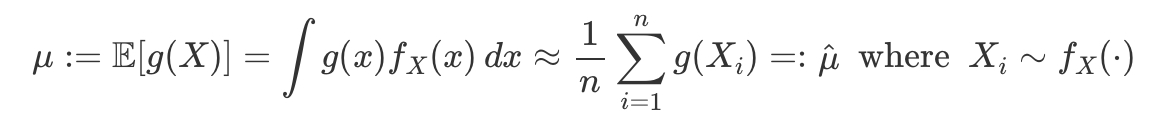
importance sampling

E[Xh(X)] = … and Ef[Xg(X)] = …

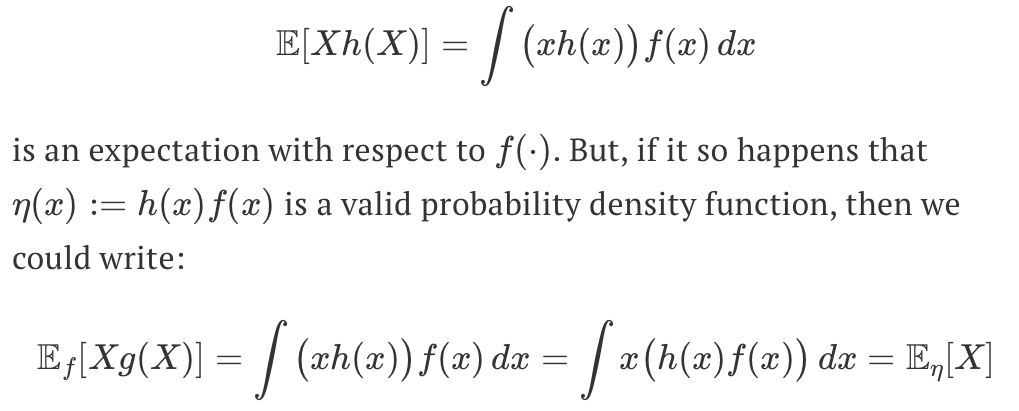
theorem 5.3 - μhat

theorem 5.4 - the variance of the importance sampling estimator

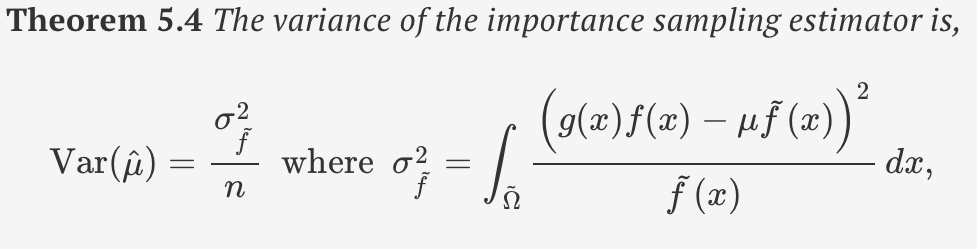
optimal f tilda (x)

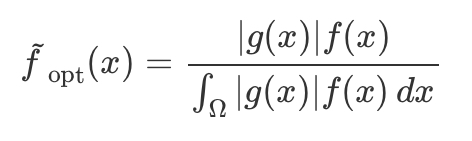
self-normalised importance sampling

approximate estimate and what is uses

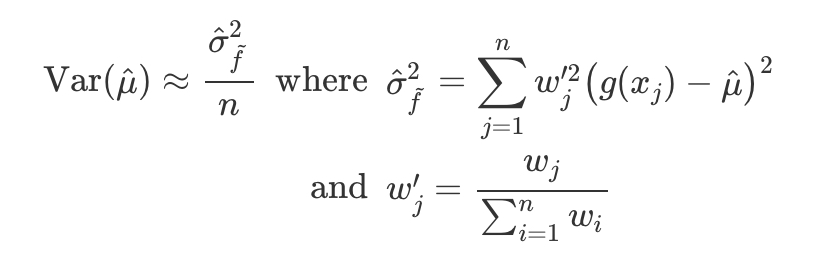
theoretical optimal proposal in the self-normalised weight case

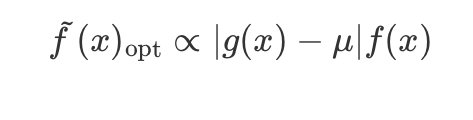
effective sample size