6: biophysical and diffraction

describe spectroscopic vs diffraction methods

spectroscopy

• rely on transition between energy levels

• vary wavelength of radiation = absorption/emission occurs at given frequencies

• sample (typically) in solution

diffraction

• interaction with matter

• keep wavelength fixed = measure variations in intensities with incident direction

• sample in solid state

simply describe x-ray diffraction

x-rays = similar wavelength to the spacing between atoms in sample

x-rays are focused on sample. x-ray are reflected by electrons surrounding atoms of the sample, changing the direction by theta. these scattered x-rays constructively interfere to produce a diffraction pattern.

describe diffraction on different types of material

i.e. fibres, single crystals, powders

product different diffraction patterns = same theory applies to interpret them

what range are x-rays?

0.01 → 10 nm

~ distances between atoms

what kind of scattering is x-ray diffraction?

elastic

• energy maintained

• direction altered

describe the photoelectric effect

when a photon strikes an atom/molecule and transfers its energy to inner-shell electron.

if the photon has sufficient energy (≥ electron binding energy), the electron is ejected from its shell

ejected electron = photoelectron

describe the generation of x-rays

x-ray tube containing:

• cathode (-ve) = source of electrons ~ tungsten

• metal anode (+ve) = target ~ copper

• vacuum

a current is passed through the cathode, which heats up and emits electrons. these electrons are accelerated through the vacuum to target, gaining kinetic energy. when electron hits the anode target, kinetic energy is converted to:

• heat (major): anode must be cooled due to release of heat

• x-rays (minor): if the incident electron has enough energy, it can knock out 1s electron from the K-shell (innermost electron shell) of the anode atom = ionisation. K-shell vacancy is filled from a higher energy shell (L-shell/M-shell), releasing energy in the form of an x-ray (photons with x-ray wavelength)

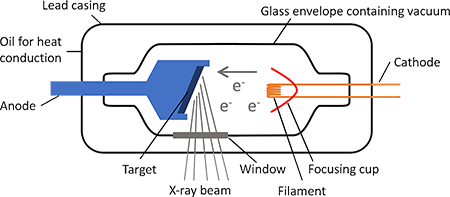
what are the two types of x-rays which can be produced by x-ray tubes?

• characteristic x-rays

• Bremsstrahlung radiation

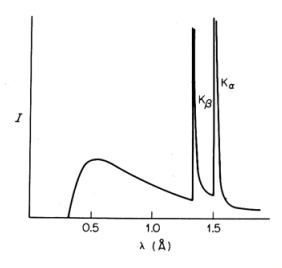
what are characteristic x-rays?

x-rays produced by x-ray tube

= energy/wavelength is specific to size of X→K transition

= energy/wavelength is specific to anode element

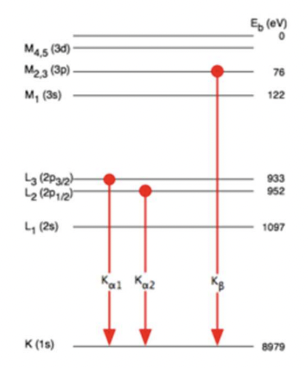
what are the different shell labels?

K: n=1

L: n=2

M: n=3

what gives rise to the different types of K radiation?

due to SO coupling splitting the degenerate 2p/3p orbitals

= different size transitions

describe Bremsstrahlung radiation

when electron decelerates rapidly as they interact with electric field of the nucleus, they can produce broad-spectrum X-rays that can vary in wavelength and are not specific to the anode element

what is the general equation for x-ray absorption? *not given*

I = intensity of radiation after passing through material

I(0) = intensity of incident radiation

µ = absorption coefficient of the material (dependent on material and X-ray wavelength)

t = path length 

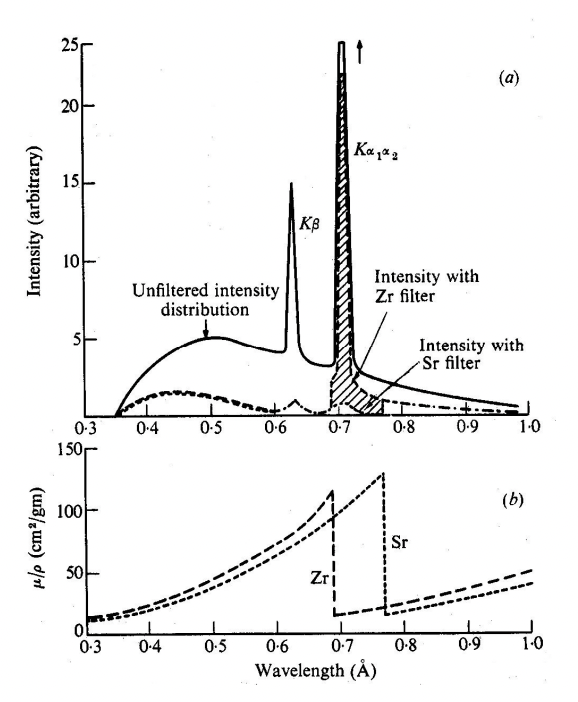
describe filters

selectively remove unwanted x-ray radiation from spectrum, particular K(B)

K(B) = contributes to background noise/reduce image clarity

= have large absorption coefficients, µ, at certain wavelengths corresponding to K(B)

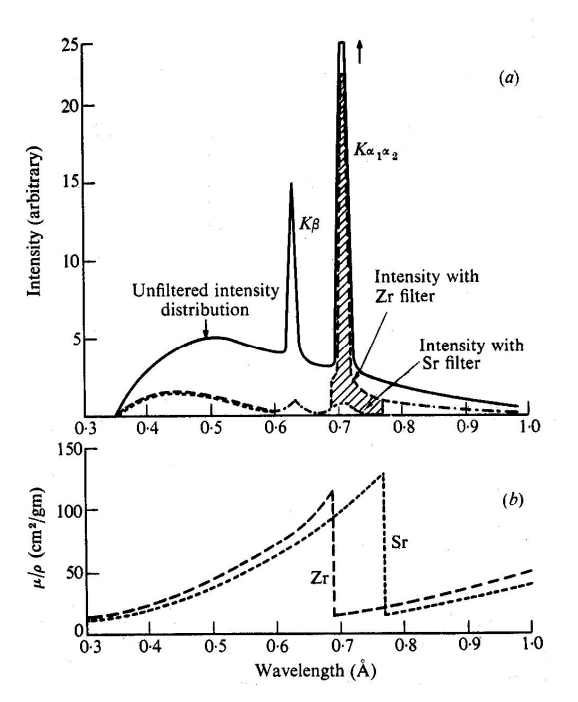
describe absorption edges

sudden increase in absorption of X-rays (absorption coefficient) above threshold energy to excite an electron from an inner atomic shell

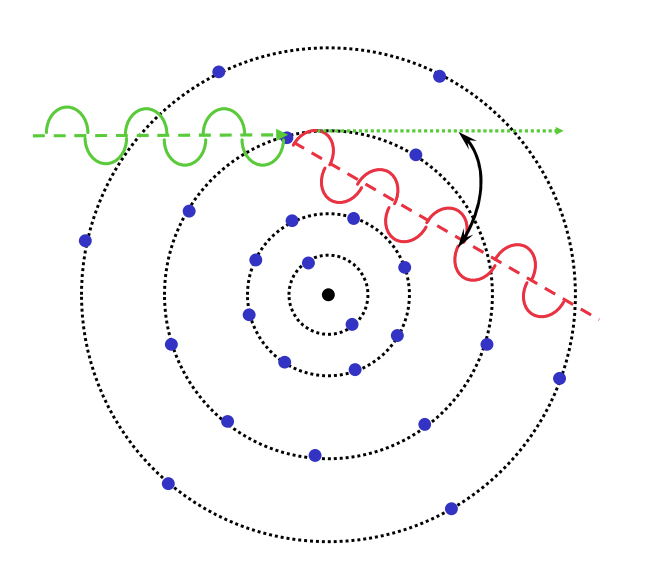
what are 3 types of x-ray interaction with material

• Thompson scattering

• Compton scattering

• photoelectron absorption

describe scattering

the redirection of incoming radiation (photon in x-ray) due to interaction with matter (electrons in x-ray)

describe Thompson scattering

wave:

• elastic scattering = no loss of energy

• coherent scattering = no change in frequency/wavelength of photon = no energy transfer between photon and electron

• wave is scattered in all directions = varying angles

electron:

no electron is ejected

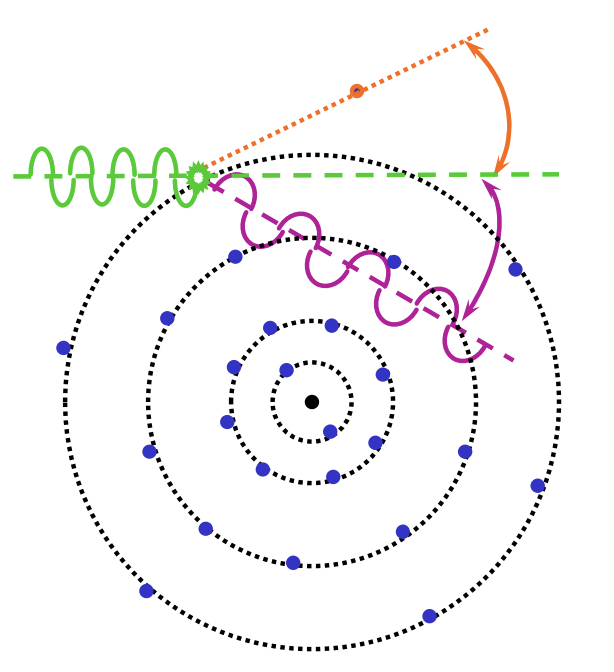
describe Compton scattering

wave:

• inelastic scattering = loss of energy

• incoherent scattering = decrease of frequency/increase in wavelength = energy transfer between photon and electron

• wave is scattered in all direction = varying angles

electron:

outer shell (loosely bound) electron is ejected

describe photoelectron absorption

wave:

• inelastic scattering = loss of energy

• no scattering = complete energy transfer between photon and electron

• no wave

electron:

inner shell electron is ejected = photoelectron

excess absorbed energy released as:

• x-ray fluorescence (not scattered) = photoelectric effect

• Auger electron = energy transferred to another electron and ejected

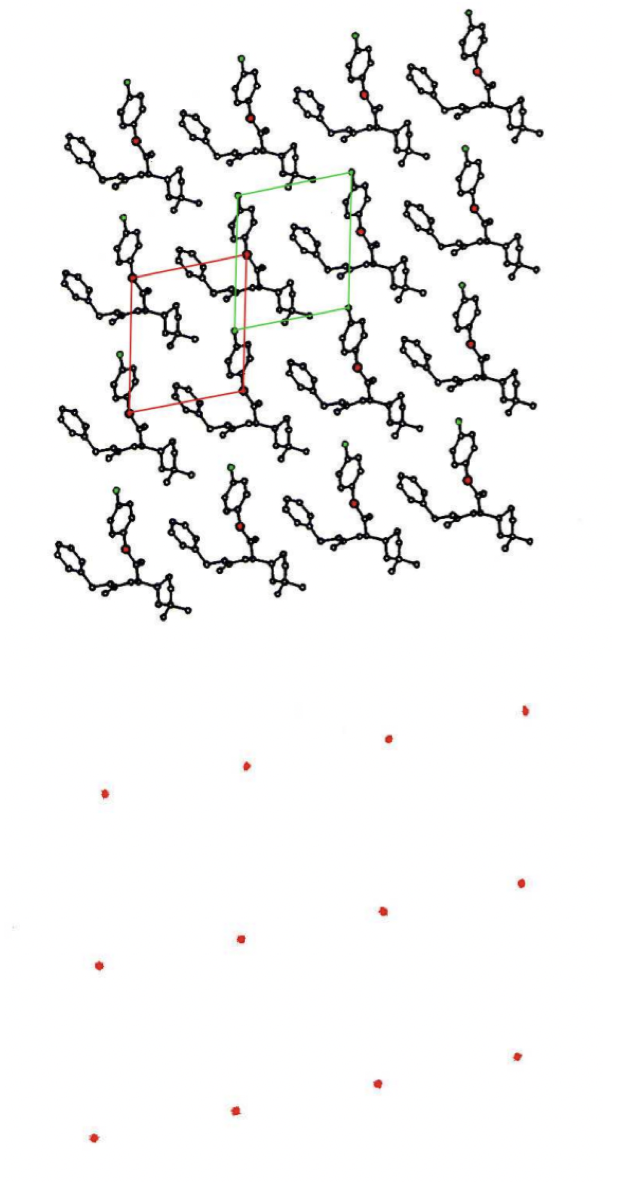
why are crystals used in x-ray diffraction?

electron scatter x-rays very weakly

= use ordered arrays of molecules

define structural units

structural unit = repeated by translation in 3 dimensions = all orientated identically

crystal lattice structure can be represented by structural units as single points

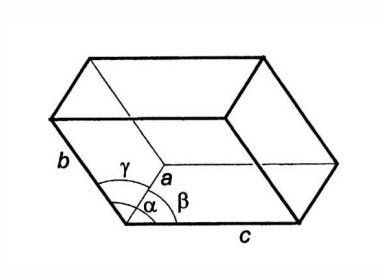
describe unit cell

smallest repeating unit of the lattice

 parallelepiped (6 parallelogram-faced structure) with:

• three edges (a, b, and c i.e. x, y, and z)

• three angles (a, B, and Y)

convention:

a < b

Y ~ 90°

contains 1 whole molecule in total

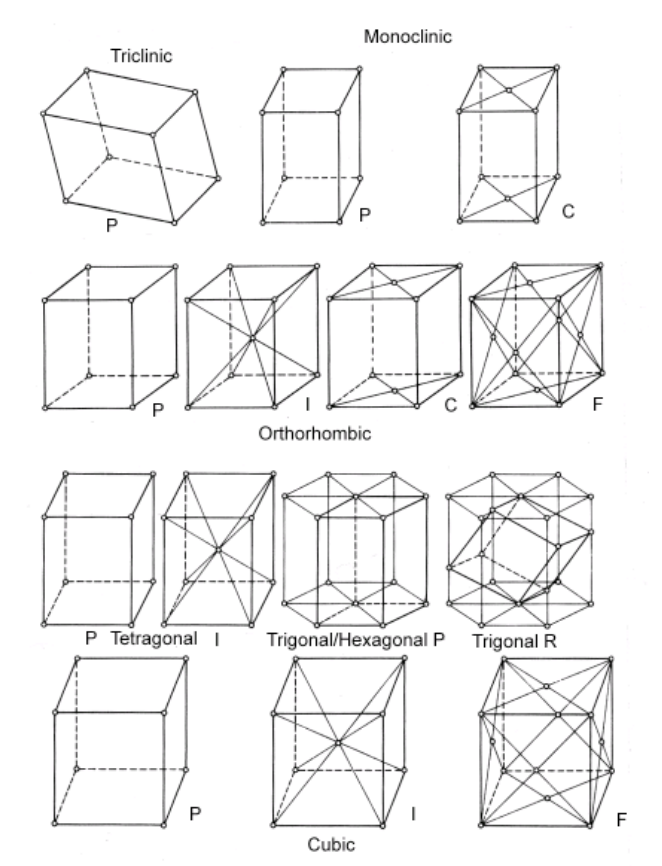
what are the 14 distinct lattice types which symmetry operations yield?

Bravias lattices

what are the 7 crystal systems of Bravias lattices?

• triclinic

• monoclinic

• orthorhombic

• tetragonal

• rhombohedral

• hexagonal

• cubic

what are the different labels within each crystal system?

P = primitive = only points in each corner

I = body-centred

F = centred in all 6 faces

C = centred on 2 opposite faces

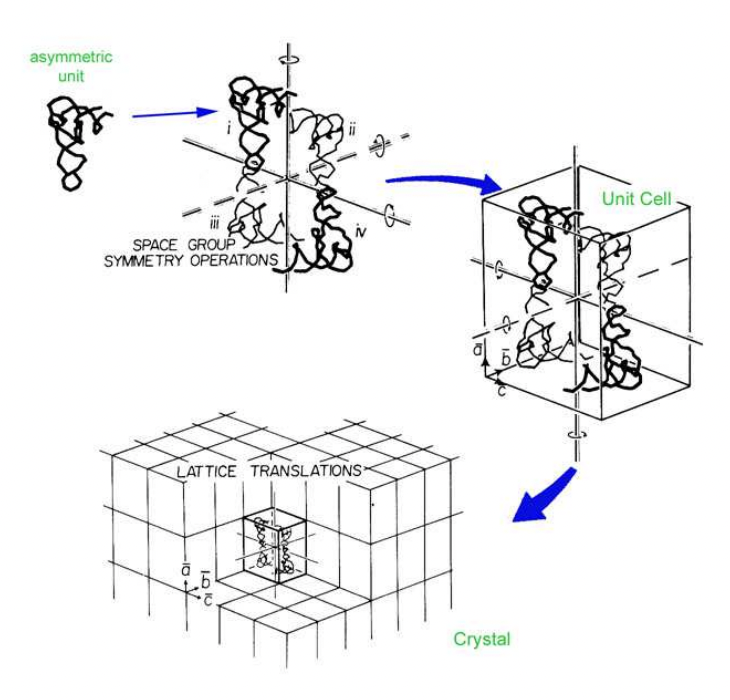
define asymmetric unit

smallest section of the unit cell/crystal structure related by symmetry

summarise crystalline structure

asymmetric unit -(space group)→ unit cell → crystal

space group = symmetry operations which generate unit cell from asymmetric unit

what are 3 types of interference?

• intermediate

• constructive

• destructive

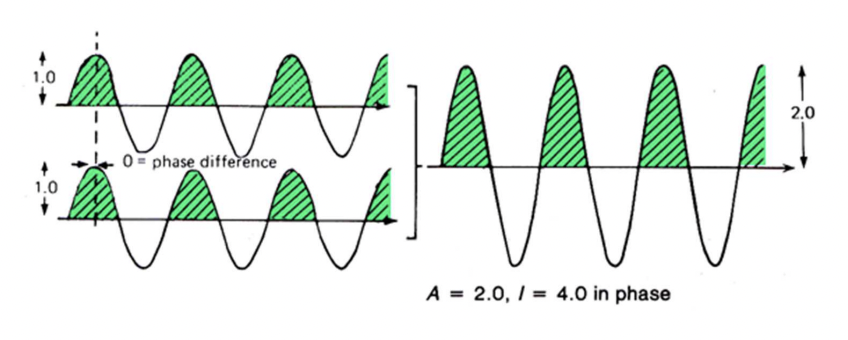
describe constructive interference

• waves in phase: phase difference = 0

• total reinforcement

• A = single wave + single wave = 2*single wave

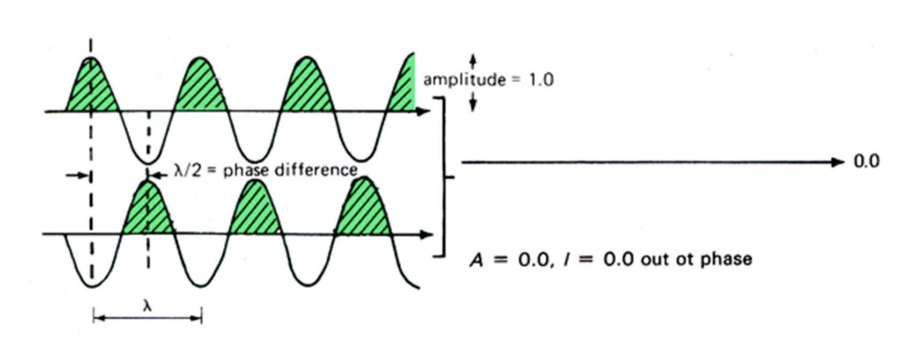
describe destructive interference

• waves out of phase: phase difference = λ/2 or 180°

• complete cancellation

• no resultant wave

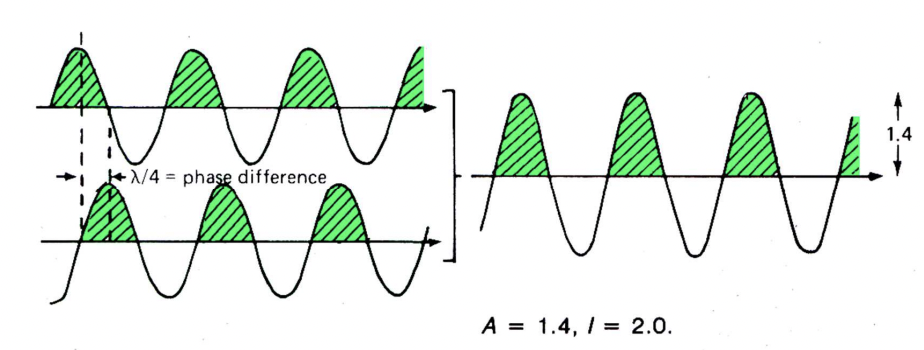
describe intermediate interference

• waves partially in phase: i.e. phase difference = λ/4 or 90°

• partial reinforcement

what kind of interference is required for x-ray diffraction?

constructive interference

describe the features of a diffraction pattern

• geometry

• intensities

• symmetry (of intensities)

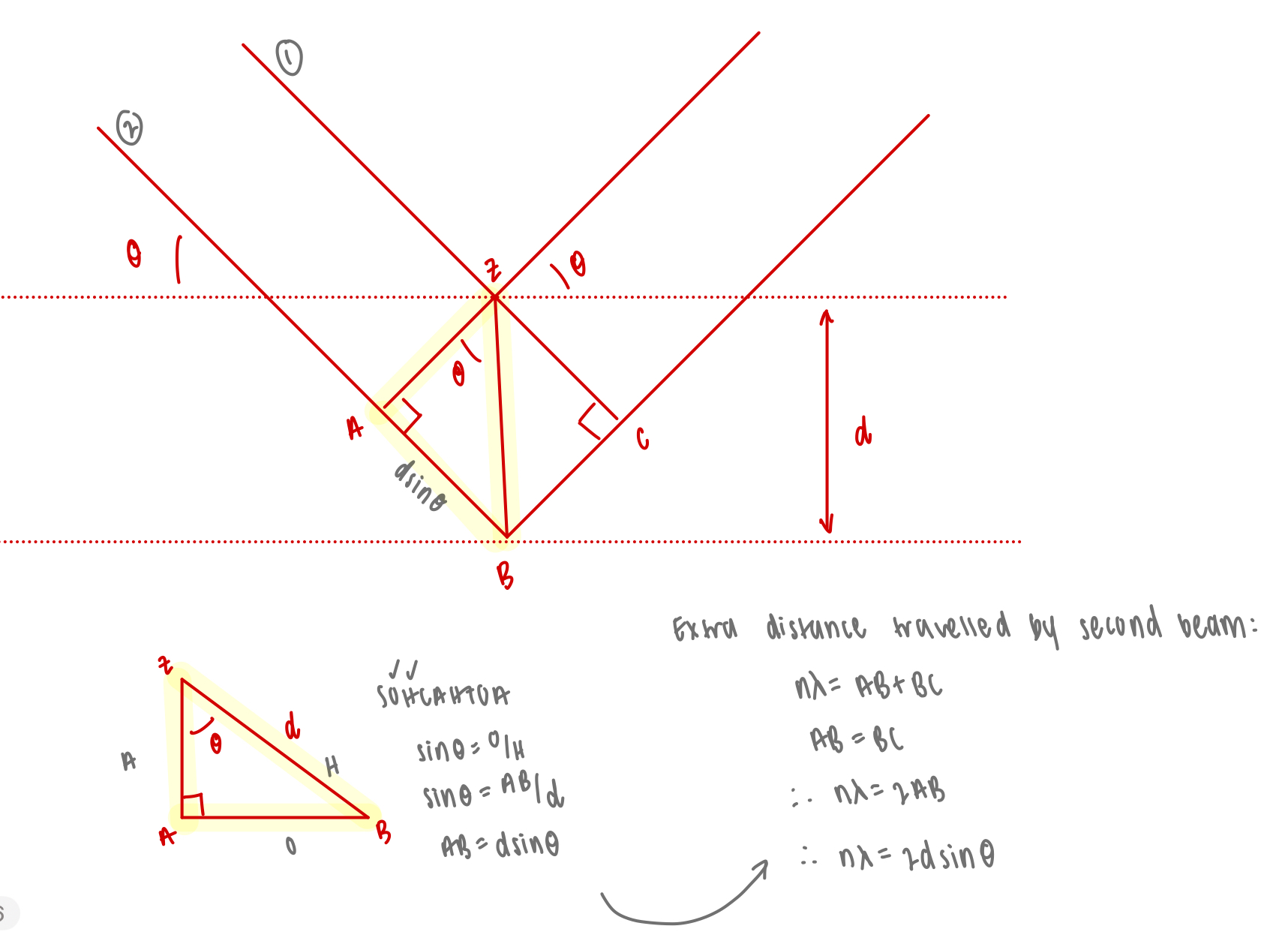
describe Braggs law

incident x-ray onto a crystal surface at angle θ will be reflected by different crystal ‘planes’ by angle θ.

when constructive interference of scattered x-rays occurs, the scattered x-rays are intense enough to be visible on the diffraction pattern.

when constructive interference does not occur, the scattered x-rays partially or completely destructively interfere.

Braggs law defines when constructive interference occurs

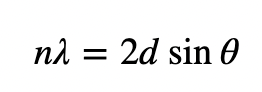
explain the derivation of Braggs law

constructive interferences will arise where the path difference is integer values of wavelength = Braggs law

describe crystal planes

simple molecules = convenient

complex molecules = difficult to see how they arise

describe scattering from point

lattice points are used as reference rather than planes

d = distance between lattice points

describe first order vs higher order diffraction

first order: n=1: path difference = λ

higher order: n>1: path difference = 2λ, 3λ, etc.

how does the angle of diffraction vary for different orders of diffraction

higher order of diffraction = larger n = larger angle of diffraction

lower order of diffraction = smaller n = smaller angle of diffraction

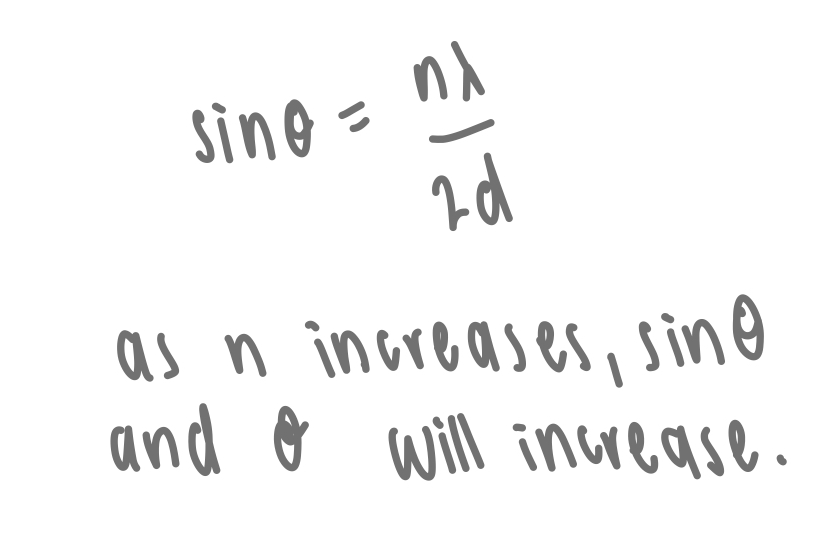
describe the reciprocal lattice

inverse relationship between crystal lattice and lattice of reflections (diffraction pattern)

describe Miller indices

3 integers = h, k, l

= labels families of planes/points and reflection is corresponds to that give rise to diffraction spots due to constructive interference (also a label for the resulting reflection)

define the Laue equation *given*

used to determine d-spacing between planes/points of an given reflection

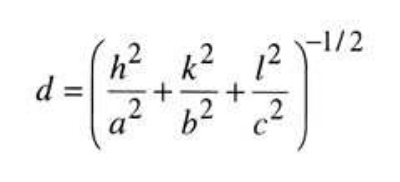
what is the unit angstrom?

A = x10^-10 m

what controls the position vs intensity of diffraction pattern

position = d spacing and Bragg angle = arrangement of unit cells:

• crystal structure

intensity = extent of constructive interference = arrangement within unit cells:

• unit cell structure

describe the application of diffraction spot positions

can be used to determine the Bragg angle = used to determine d

• crystal symmetry

• unit cell dimensions

• estimare molecules in asymmetric unit

define the structure factor, F, and its amplitude, |F|

F = mathematical function describing the amplitude and phase of a wave diffracted from crystal lattice planes characterised by Miller indices h,k,l.

|F| = strength/intensity of diffracted wave

describe the application of diffraction spot intensities

I(hkl) = intensity of diffraction spot ∝ extent of constructive interference

F(hkl) = structure factor for given (hkl) indices

| F(hkl) | = amplitude of the wave scattered by one unit cell at (hkl) indices

larger amplitude = more constructive interference

smaller amplitude = less constructive interference

hence, amplitude of scattered wave ∝ intensity of diffraction spot

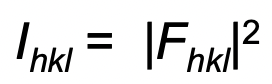
describes waves represented as vectors

vector = F

amplitude = |F|

direction = φ

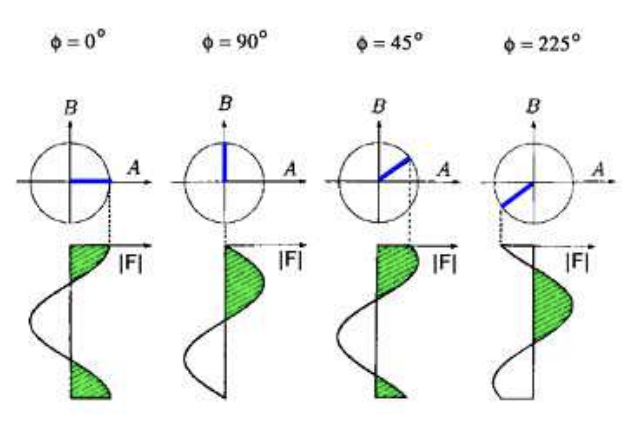
what equations define waves as vectors? *not given*

know the cos and sin

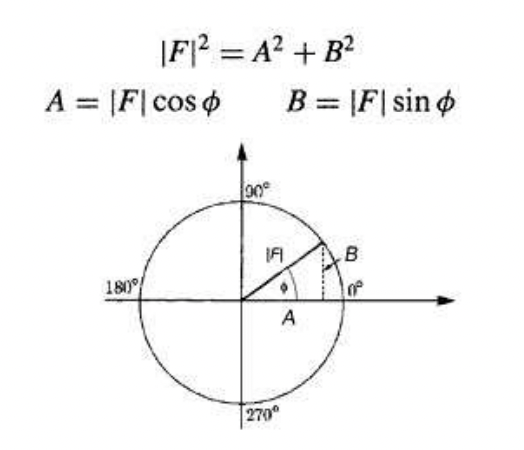
describe the phase problem

= phase information is lost during XRD

varying degrees of constructive interference between waves give rise to diffraction spots of varying intensities. the respective phases cannot be determined through the intensity of the diffraction spots.

there is no way to directly measure the phase (individual contribution to constructive interference) of the constituent waves

knowing the amplitude and phase of the initially scattered waves, how can the amplitude and phase of the final scattered wave be determined?

addition

find total A and total B

find total |F| and φ

describe structure factor vs structure factor amplitude

F = structure factor = complex

|F| = structure factor amplitude = not complex

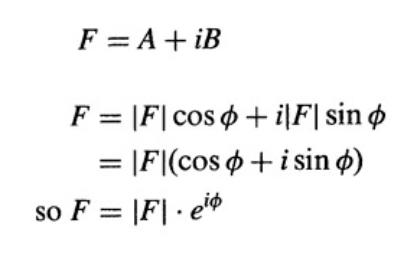
describe atomic scattering factor

= measure of scattering power of an isolated atom = unique to an atom

= f(Φ)

depends on:

• scattering amplitude of an isolated atom

• Bragg angle of scattering

describe f(Φ) when Φ=0 (forward direction)

all electron scatter x-rays exactly in phase = no path difference

all scattered waves combine constructively

maximum scattering

describe f(Φ) when Φ>0

partial destructive interference increases as Φ increases

= intensity falls of as Φ increases

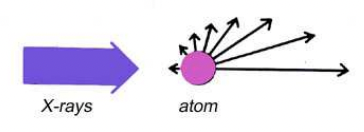
describe the effect of temperature on f

increased T = increased vibrations = spread out electron density = increases interference effects = scattering factor (f) falls off faster

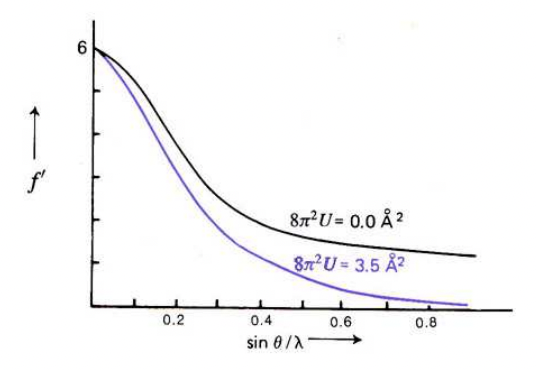
what is U?

= isotropic displacement parameter

= describes how much an atom deviates from its ideal position within a crystal lattice due to thermal vibrations

∝ 1/f

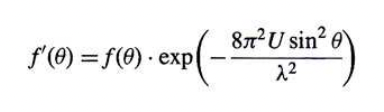
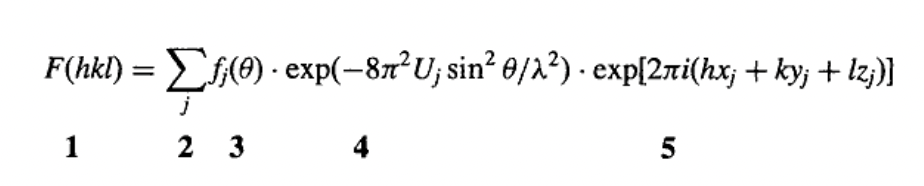
define the structure factor equation

2, 3, 4 = sum of the scattered x-rays

5 = scattered waves from each atom have different relative phases in direction hkl which depends on positions of atoms

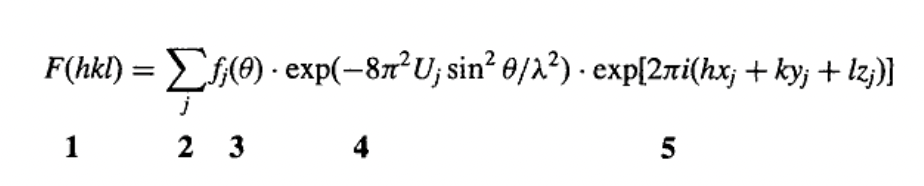
what is required to calculate structure factor, F?

• chemical type (f)

• position (xyz)

of each atom is known

describe the Fourier series

any periodic function can be described as a sum of simple series sin/cos functions

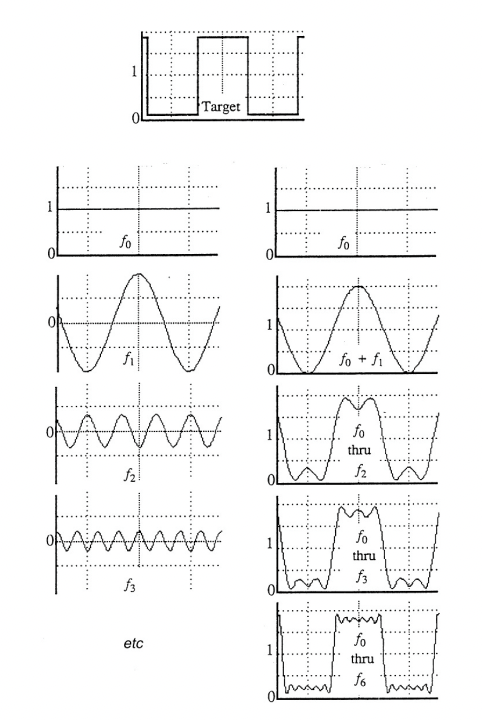
describe how the diffraction pattern is related to real space lattice

diffraction pattern → reciprocal lattice -(Fourier transform)→ real space lattice

what are methods of solving the phase problem

• heavy atom method

• direct method

describe the heavy atom method

substituting small number of atoms in the crystal with atoms of high atomic number which scatter X-rays more strongly and giving intense and detectable diffractions

diffraction pattern compared to normal diffraction patterns

Patterson function helps identify relative positions and phase information

describe the Patterson function

= Fourier transform of the squared amplitudes of structure factors F with all phases set to 0

= technique to determine electron density map purely on intensities of diffraction

= vector relationship

what is the height of Patterson peaks dependent on?

atomic numbers

often largest peak/atom is located at the origin

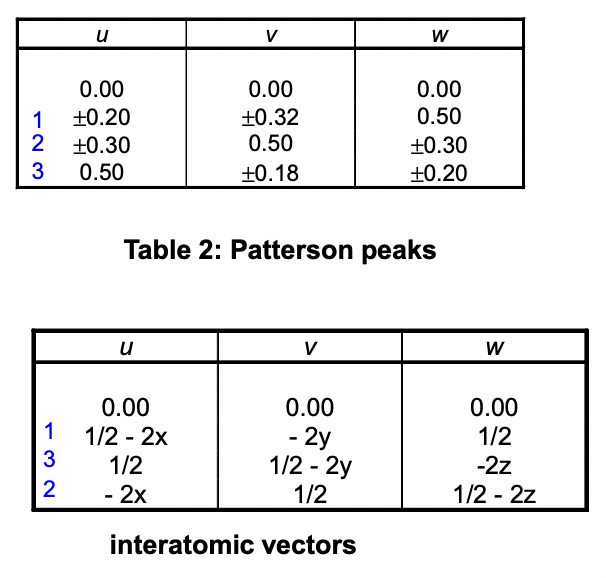
describe how interatomic vectors are found

subtracting the ‘central’ symmetry/origin from all the other symmetries

origin = simplest symmetry operator

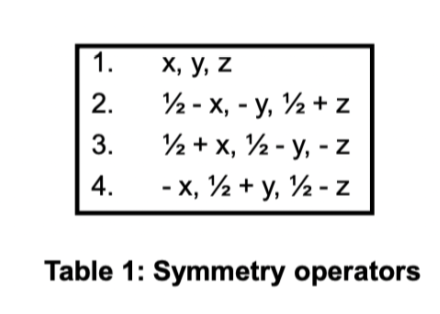
calculate the interatomic vectors here

• find interatomic vectors

• match with patterson peaks (1/2 = 0.5)

• rearrange to find x,y,z

x = 0.15

y = 0.16

z = 0.5

describe direct methods

guess then modify using probability and real-space constraints i.e. electron density must be +ve or 0

take the strongest E values only

phase signs are important = determine constructive/destructive interference

describe how the signs of the phases of reflection relate

products of the sign of two reflections is approximately equal to the sign of the sum of two reflections

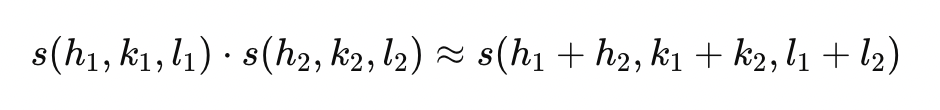
describe the application of heavy atom/direct methods for the structure factor calculation

provide (approximate) positions and chemical type

= obtain phase α(calc) from F(calc)

what are the two methods to find the structure factor

heavy atom/direct method → → F(calc) → → Fourier map

intensity of diffraction spots → → F(obs) → → Fourier map

list the necessary steps and calculations required to solve and then complete a single crystal X-ray structure

• calculate P(uvw) (Patterson function/map) and find heavy atoms

• calculate xyz of known atoms ^

• compute |F(calc)| → α(calc) (approximate phases)

• calculate p(xyz) from |F(obs)| and α(calc) -Fourier transform→ Fourier map

• Fourier map → more atomic positions

• refinement = step 2 and repeat

what are parameters of the refinement process?

• R factor

• difference maps

• S

describe R-factors

R measures the agreement between observed structure amplitude and calculated (model) structure amplitude

small R = good model

large R = bad model

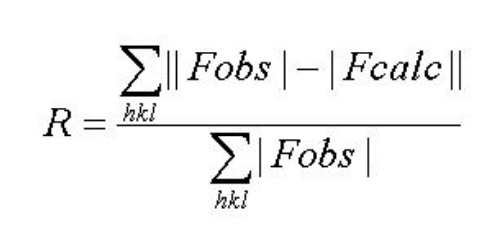
what is the application of Fourier maps

can be used to construct an electron density map

describe difference maps

 ∆p(xyz) = difference between the observed and calculated electron density at the point xyz

should be flat

+ve peak = atom omitted from model

-ve peak = wrong atom/atom position in model

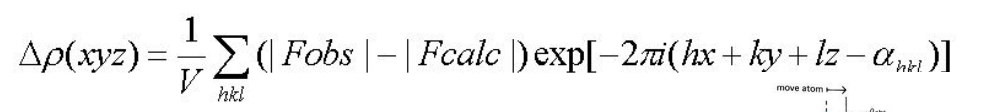
describe anisotropic temperature factors

anisotropic atomic motion can be described by 6 parameters which improve the fit of F(calc) with F(obs)

describe hydrogen atoms in electron density map

• H = 1 e = weak scattering of X-rays

• electron density shifted towards bond

often only discernible from difference map

describe the method of least squares

approach to refine models of best fit experimental data

S = residual sum of squares = quantities difference between obs and calc = want to minimise S

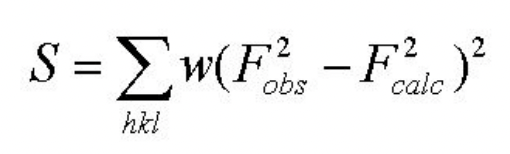
describe neutron diffraction

thermal neutrons have same wavelength as X-rays

X-rays = interaction with electron clouds (scattered by)

neutrons = interact with nuclei (scattered by)

diffraction pattern depends on:

• nuclear scattering length = constant for a nucleus/isotope = +ve or -ve (constructive/destructive)

• nuclear position

• INDEPENDENT OF θ

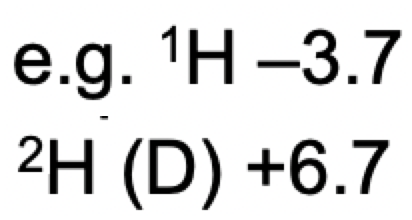
compare neutron scattering and x-ray scattering

xray scattering » neutron scattering

what is an application of neutron diffraction

distinguishing between isotopes in a structure

e.g. (1)H and (2)D

describe powder diffraction

combines diffraction patterns of a single crystal for all possible orientations of the crystal

= broad, diffuse pattern

also possible to resolve mixtures

describe a diffraction peak profile

FWHM = full width at half maximum = B = measure of peak breadth

large B = small crystal

small B = large crystal

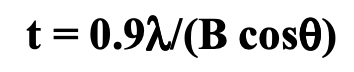
describe the different effects on B

inst = instrumental factors i.e. resolution

strain = distortions to crystal lattice

uniform strain: change in position of peak (uniform change in d/Bragg angle)

non-uniform strain: peak broadening (diffuse change in d/Bragg angle)

what are the different ‘levels’ of protein structure

primary = amino acid sequence

secondary = local polypeptide folding due to H bonding

tertiary = 3D folding of entire polypeptide chain due to interactions of R groups

what defines the absolute entropy of any object not given

w = number of possible states

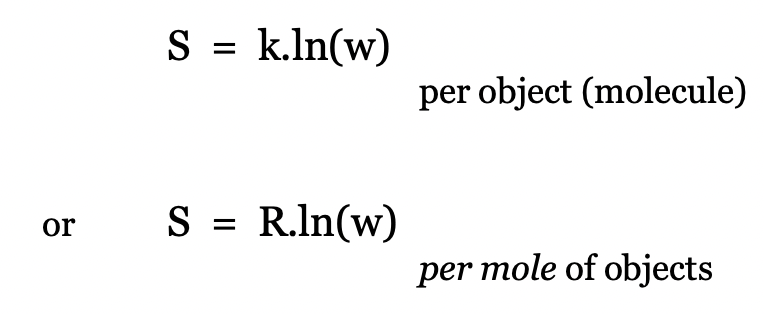
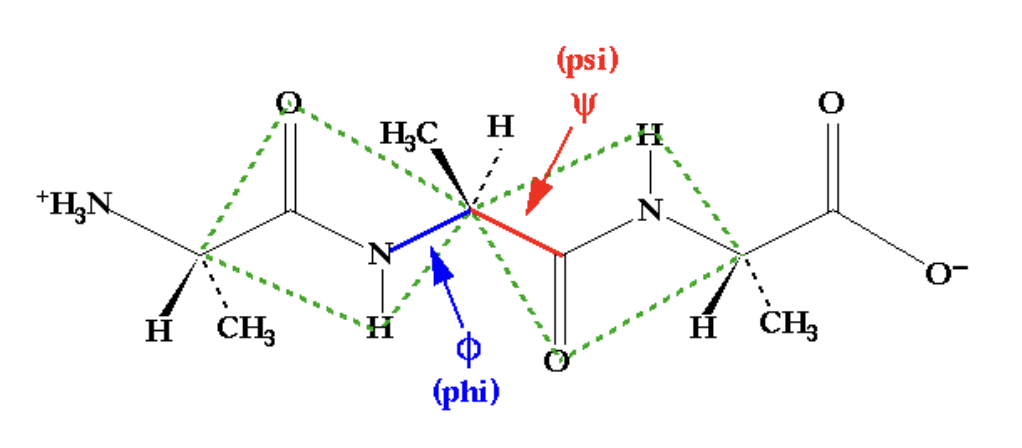
define the possible conformation of a peptide

psi ~ 3

theta ~ 3

hence 9 possible conformers for each peptide (ignoring side chains)

define the absolute entropy of peptide in a random coil

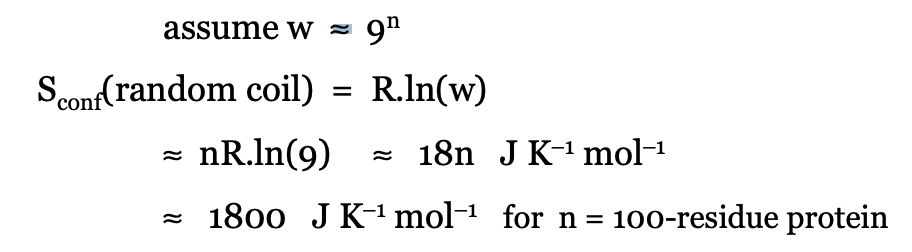
define the absolute entropy of peptide in native conformation

describe the free energy change of folding in terms of entropy

largely unfavourable

must be compensated for by H

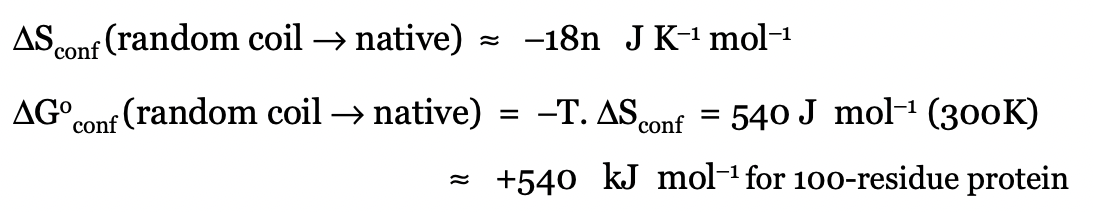
describe the directional folding of proteins

secondary structure = low energy conformation

molten globule structure = hydrophobic interactions

stabilisation of folded structure = directional H bonds

what are types of non-covalent interactions

• electrostatic

• H bonding (extreme electrostatic)

• hydrophobic

what are types of electrostatic interaction (exc H bonding)

• charge-charge

• charge-dipole

• dipole-dipole

• dipole-induced dipole

• transient dipole-induced dipole

describe the value of potential V

-ve = attractive

+ve = repulsive

define coulombs law

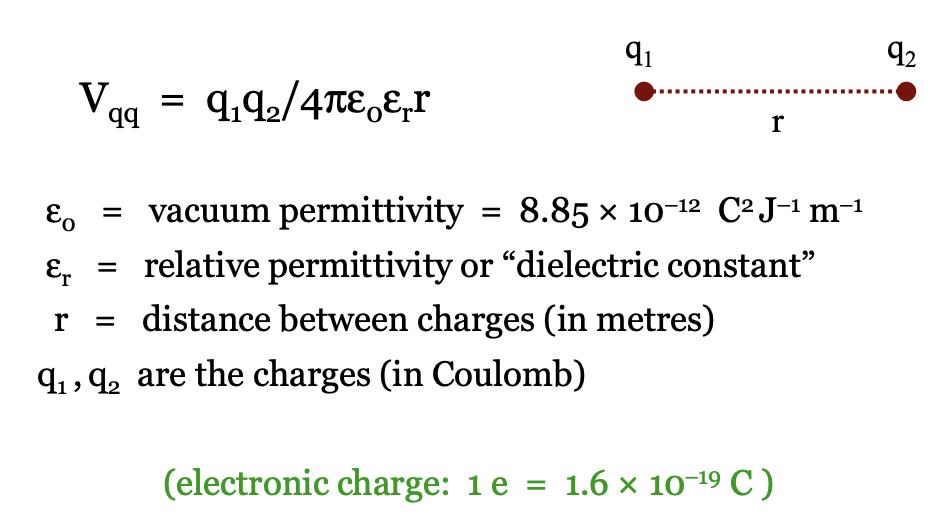
what can reduce V of coulomb interaction?

• relative permittivity/dielectric constant

• ionic screening

describe electrostatic interactions in vacuum vs water

water ««« vacuum

= ionic screening