Chapter 4 Exercises: Venn Diagrams for Immediate Inferences (Symbolic Logic)

venn diagram

a diagram that uses interlocking circles to represent classes

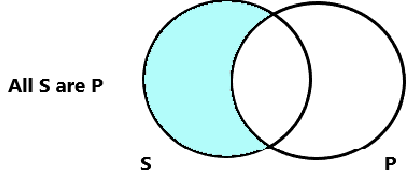
Diagram an A Statement

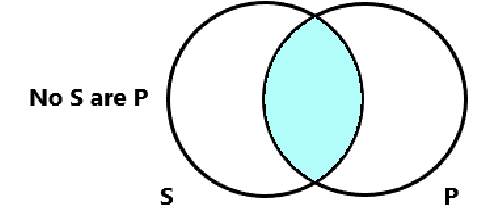
Diagram an E Statement

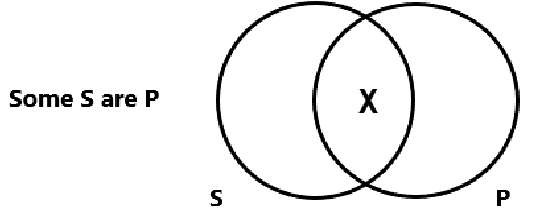
Diagram an I Statement

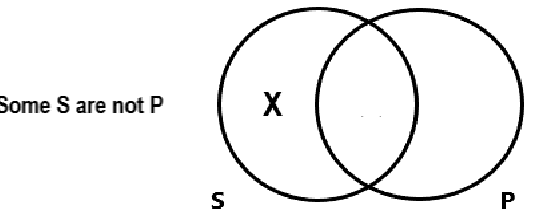
Diagram an O Statement

False

True or False: If there are no marks in an area of a Venn Diagram, this means that nothing exists in that area.

diagram its contradiction

How do we diagram a statement that’s given to us as false?

X in Area 2

Diagram the statement:

It’s false that no scientists are chemists.

Shade Area 1.

Diagram the statement:

It’s false that some squares are not quadrilaterals.

1. Diagram the premise.

2. Check to see whether the information in the conclusion is already in the diagram (it must be in the SAME PLACE). If yes, then it is valid. If no, then it is invalid.

How are Venn diagrams used to test immediate inferences?

True

True of False: If the conclusion of an argument does not state anything not already stated in the premise(s), then the inference is valid.

reduce terms
can use contraposiion or obversion for this example because it is an O Statement

Diagram: X in Area 1.

Invalid

What can we do if the number of terms in an immediate inference exceeds two, such as in the case below?

1. Some non-M are not non-O.

2. So, some M are not O.

Premise is an A statement, so you can use contraposition or obversion.

Diagram: Shading in Area 2

Valid

Reduce the number of terms in the inference below and test it with a Venn Diagram:

1. All C are non-D.

2. So, it is false that some C are D.

1. Some animals are not dogs.

2. So, some dogs are not animals.

Provide a counterexample to the invalid form of immediate inference below (it commits the fallacy of illicit conversion)":

1. Some S are not P.

2. So, some P are not S.

1. No whales are fish.

2. So, no non-fish are non-whales.

Provide a counterexample ot the invalid form of the immediate inference below (it commits the fallacy of illicit contraposition):

1. No S are P.

2. So, no non-P are non-S.

Symbolic Form:

1. All N are O.

2. All non-N are non-O.

Counterexample:

1. All whales are mammals.

2. So, all non-whales are non-mammals.

Provide a counterexample to this invalid immediate inference:

Since every neutron star is an object with a massive gravity field, we can infer that whatever is not a neutron star is not an object with a massive gravity field.

Shaded in Area 2

Invalid

Evaluate the argument with a Venn Diagram:

1. No bears are mammals.

2. So, some bears are mammals.

Symbolic Form:

1. Some M are not D.

2. It is false that all M are D.

Diagram: X in Area 1.

Valid

Evaluate the argument with a Venn Diagram:

Some motorcycles are not dirt bikes. Therefore, it is false that all motorcycles are dirt bikes.

Symbolic Form:

1. No L are S.

2. So, it is false that some L are S.

Diagram: Shading in Area 2

Valid

Evaluate the argument with a Venn Diagram:

No lampreys are sharks. So, it is false that some lampreys are sharks.

Diagram: Shading in Area 1

Invalid

Evaluate the argument with a Venn Diagram:

1. All rubies are gems.

2. So, some rubies are gems.

Diagram: X in Area 2

Valid

Evaluate the argument with a Venn Diagram:

1. It is false that no nephrologists are doctors.

2. So, some nephrologists are doctors.

Diagram: Shading in Area 2

Invalid

Evaluate the argument with a Venn Diagram:

It is false that some metals are insulators. Hence, some metals are not insulators.

Diagram: Shading in Area 1

Valid

Evaluate the argument with a Venn Diagram:

It is false that some koalas are not bears. For all koalas are bears.