3- Work and energy

year 1 sem 1

What is the equation describing the motion of a particle under the action of a net force?

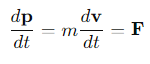
p= momentum

m= mass

v= velocity

F= the net force.

What is the equation of motion for a particle moving along the xxx-coordinate under the influence of a position-dependent force?

m =the mass of the particle

v =the velocity

F(x)= the force as a function of position.

What is the equation describing the motion of a particle under the action of a net force?

p= momentum

m= mass

v= velocity

F= the net force.

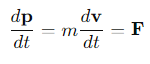
What is the equation of motion for a particle moving along the xxx-coordinate under the influence of a position-dependent force?

m =the mass of the particle

v =the velocity

F(x)= the force as a function of position.

What is the formula for velocity as a function of position?

v₀= initial velocity ​at position x_0​

v₁= final velocity​ at position x_1​.

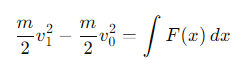
What is the Work-Energy Theorem in its general form?

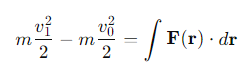
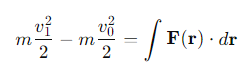
What does the left-hand side of the Work-Energy Theorem represent?

The change in kinetic energy of the particle.

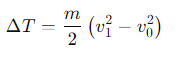
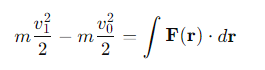
What does the path integral in the Work-Energy Theorem represent?

• The work done by the force F as the particle moves along its path.

• It is calculated by summing the scalar products of force and displacement along the trajectory of the particle.

How is work defined in the context of the Work-Energy Theorem?

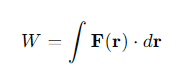
What does the Work-Energy Theorem imply about the relationship between work and kinetic energy?

The work done by the net force acting on a particle is equal to the change in the particle's kinetic energy

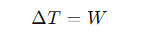
What type of quantity is work?

Work is a scalar quantity. It can be:

• Positive: When kinetic energy increases.

• Negative: When kinetic energy decreases.

• Zero: When kinetic energy remains constant.

What is the formula for power?

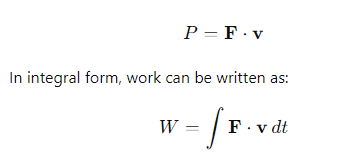
What equation relates force to potential energy?

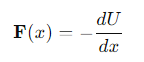
How is the work done by a conservative force expressed in terms of potential energy?

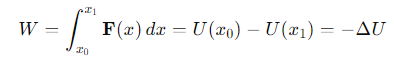
What is the Work-Energy Theorem for conservative forces?

The change in kinetic energy equals the negative change in potential energy

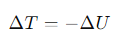
What is the conservation of mechanical energy in the context of conservative forces?

The total mechanical energy (kinetic energy + potential energy) remains constant

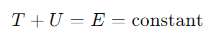
How do we define conservative forces in three-dimensional space?

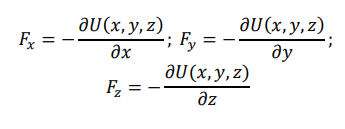
What is the formula for the vector form of force in three-dimensional space?

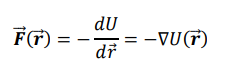
How does potential energy depend on position in conservative force fields?

• For a force acting along one axis, potential energy depends only on that specific coordinate.

• In general, for multi-dimensional motion, the potential energy function depends on all spatial coordinates x, y, and z.

What is the conservation of energy equation in the most general three-dimensional case for a conservative force?

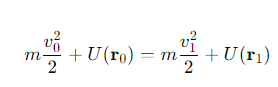
What is the law of conservation of mechanical energy for a system of interacting particles?

For a system of particles subject to only conservative forces, the total mechanical energy (the sum of the kinetic and potential energies of all particles) remains constant over time.

How can you determine if a force is conservative?

There are 2 ways:

1) Find the potential energy function 𝑈(𝑥) such that the force 𝐹 is related to the negative gradient of 𝑈

2) Show that the mechanical work done by the force depends only on the initial and final positions, not the trajectory taken

How do you calculate the work done in compressing a spring a distance x?

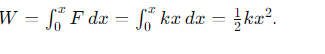
What is the formula for the elastic potential energy stored in a compressed spring?

U = the elastic potential energy

k= the spring constant

x= the displacement.

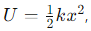
What defines a conservative force?

The work done in moving a particle from point A to point B is independent of the path taken.

What is an example of a non-conservative force?

Friction is a non-conservative force because the work done against it depends on the path taken.

How can the total force acting on a particle be expressed?

The sum of conservative and non-conservative forces

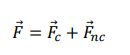
What is the generalization of the mechanical energy conservation law when non-conservative forces are present?

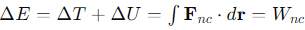
What happens to the total mechanical energy of a particle moving under conservative forces?

The sum of the kinetic and potential energies of the particle stays constant

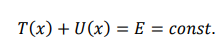
What condition must be met for motion to be possible for a particle under conservative forces?

KE must be positive

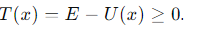
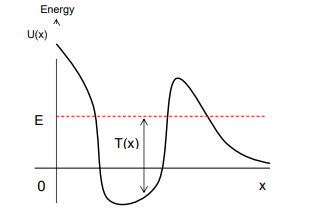
In an energy diagram, where is motion possible for a particle?

Motion is only possible in regions where U(x)<E meaning the potential energy is less than the total energy.

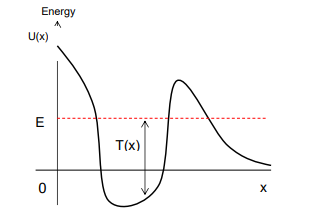
What happens when the particle’s energy is insufficient to overcome potential barriers?

The particle is "trapped" in a certain region of space, and its motion is bound.

What is a potential well and a potential barrier in the context of energy diagrams?

• A potential well is a region where the particle is bound

• A potential barrier is a region that the particle cannot cross unless it has enough energy.