Biomedical Signal Processing

Signal Processing Modules (4)

• Voltage amplifiers

• Current amplifiers

• Filters

• Comparators

Types of Voltage Signals (3)

• Continuous / Pulse

• DC / AC

• Periodic / Aperiodic

Continuous / Pulse (2)

• Continuous signals vary smoothly

• Pulse signals change abruptly

DC / AC (2)

• DC (Direct Current) has a constant voltage

• AC (Alternating Current) varies periodically

Periodic / Aperiodic (2)

• Periodic signals repeat at a regular interval, defined by period T

• Aperiodic signals do not repeat regularly

ECG (=EKG)

A periodic signal consisting of 6 pulses

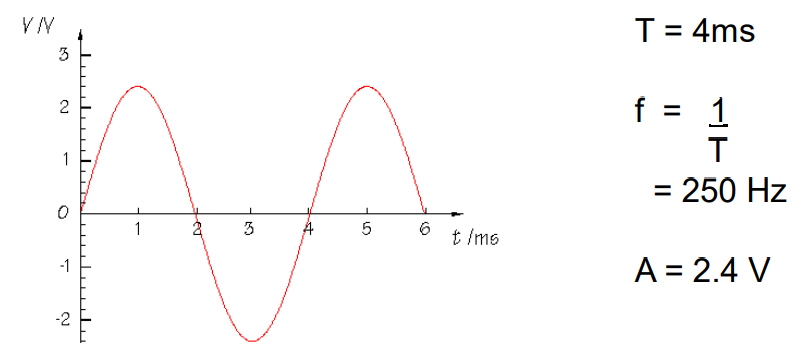
Sine Wave Voltages EXAMPLE

• Period (T) = 4 ms

• Frequency (f) = 1/T = 250 Hzf

• Amplitude (A) = 2.4 V

• Voltage Expression:
  V=A×sin⁡×(2πft)

  2.4×sin×⁡(2π×250t)=2.4sin⁡ (1586t)

In signal processing we work entirely with sine wave signals

General Formula of Sine Wave Voltages

V = A×sin×⁡(2πft+ϕ), where ϕ is the phase

Adding Sine Wave Voltages

Combining sine wave voltages of different amplitudes and frequencies can create signals of any shape.

Adding Sine Waves

Results in a not-sine wave

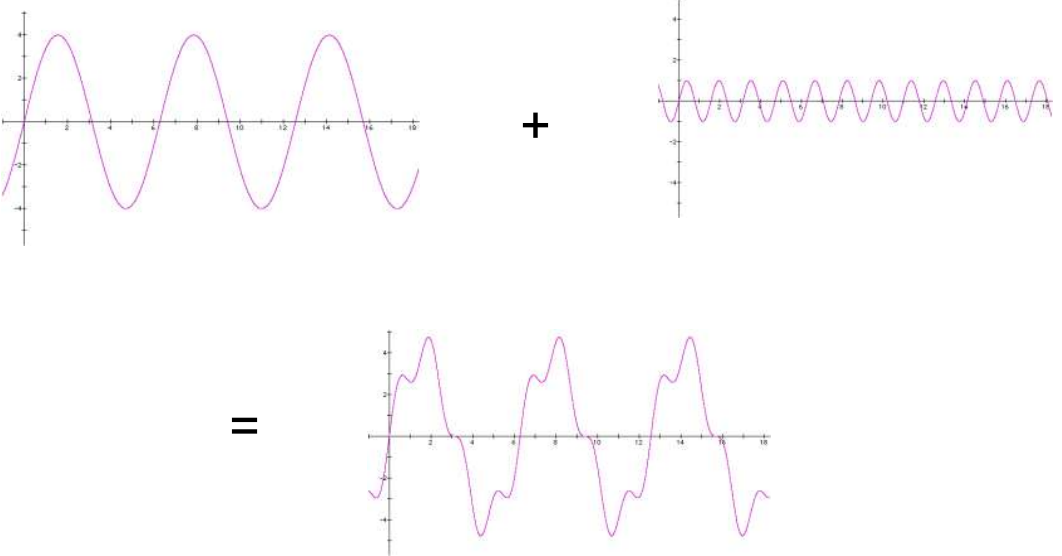
Adding Sine Wave Voltages

A = amplitude

f = frequency of sine wave

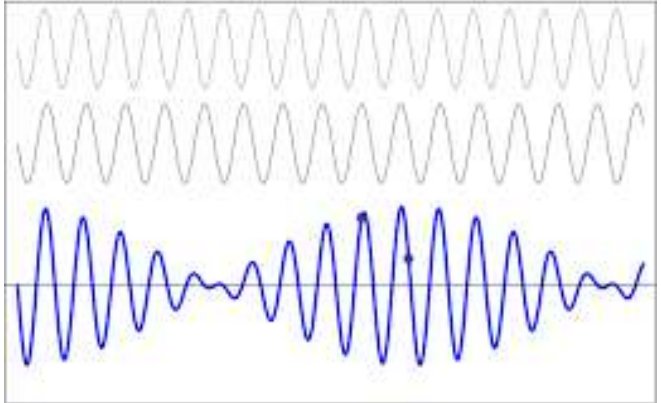
Adding two waves of equal amplitude but slightly different frequency (photo)

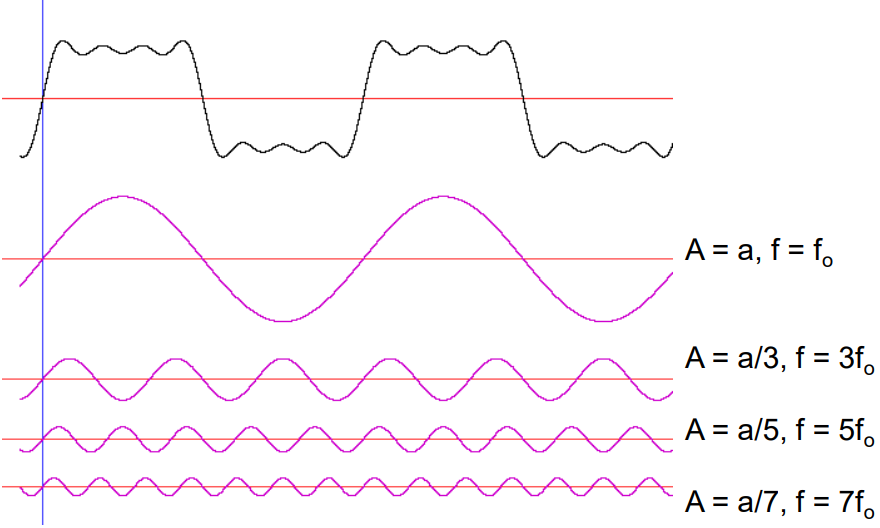
Adding Sine Waves - Producing square waves from sine waves

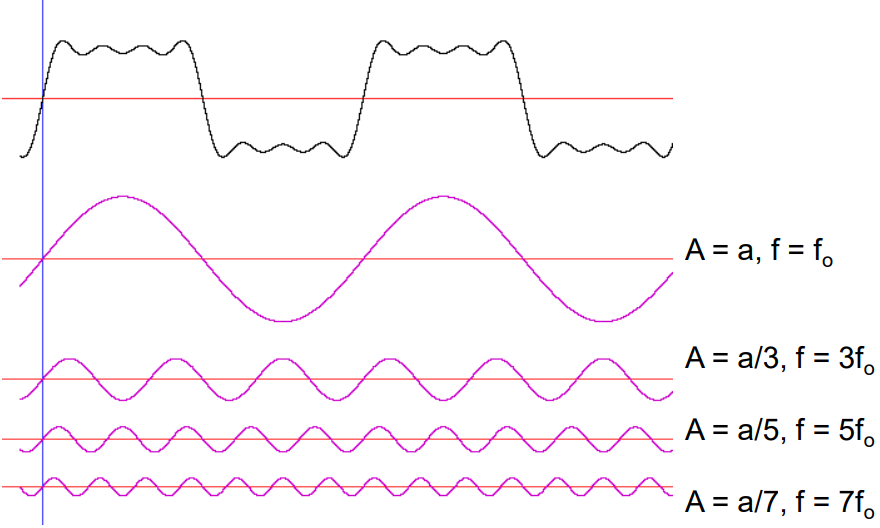
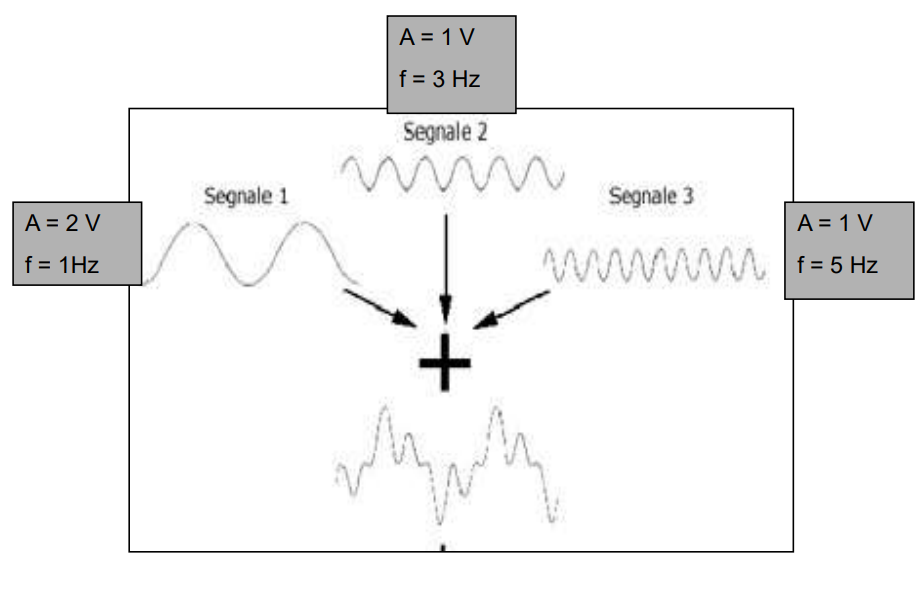
Fourier Analysis (10)

• Splitting:

  • 1st wave can be split - by a sine wave splitter

  • decompose a signal into its constituent sine waves (frequencies) and amplitudes (2-5 wave)

• Amplifying - amplifyer sine waves:

  • each of it is amplified 10x

  • multiplying the amplitude

• Reconstruction:

  • they are added together

  • results in a signal that is 10x bigger in amplitude compared to the original signal

  • becomes distorted

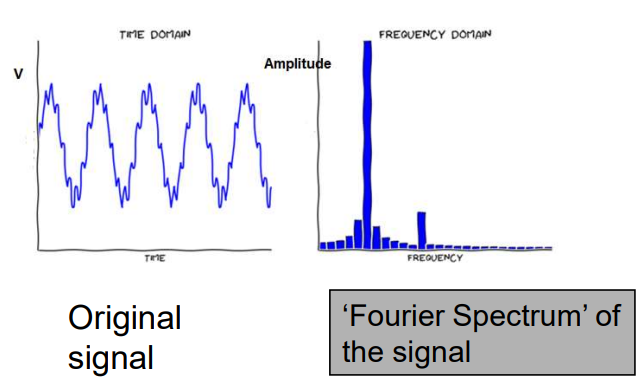
Fourier Transform

Breaks a signal into its frequency components

Inverse Fourier Transform

Any signal, regardless of shape, can be expressed as a sum of sine waves with different frequencies and amplitudes

=Reconstructs the original signal from its frequency components

Voltage Amplifiers symbol (photo)

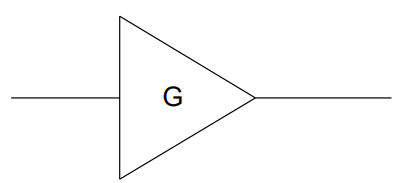
Voltage Amplifiers formula

V_out = V_in x G

G = Voltage Gain of amplifier
V_out​ = output voltage
V_in = input voltage

Amplifier Purpose

It should amplify the signal (e.g., from a patient) without altering its shape, ensuring accurate representation of the original signal

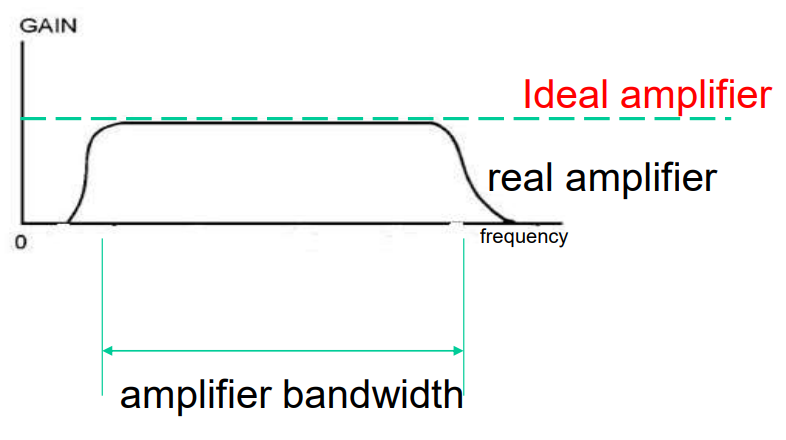
Bandwidth Limitation (2)

To avoid distortion, all frequencies in the biomedical signal's frequency spectrum must fall within the range

Amplifier's bandwidth is too narrow → fail to amplify certain frequencies → causing distortion

Frequency Response

The range of frequencies over which the amplifier maintains consistent gain

Signal distortion (2)

The alteration of the original shape or characteristics of a signal as it passes through a system

due to factors: bandwidth limitations or non-linearities

Frequency response of amplifiers

ideal and actual amplifier - never ideal

Types of Amplifiers (6)

• Voltage Amplifiers

• Differential Amplifiers

• Logarithmic Amplifiers

• Isolation Amplifiers

• Current Amplifiers

• Filters

Differential Amplifier Formula and Meaning (2)

V_out ​= (V_in1​ − V_in2​) × G

difference between two input voltages is amplified

Differential Amplifier Use (3)

ECG; spectrophotometers

Require Isolation Amplifiers*

Isolation Amplifiers (3)

• output is completely isolated from the input

• crucial for patient safety in medical applications

• preventing electrical shocks or interference between the patient and the equipment

Logarithmic Amplifier Formula and Meaning (2)

V_out ​= log (V_in1​) × G

Output is proportional to the logarithm of the input voltage

Logarithmic Amplifier Use (2)

spectrophotometers; digital x-ray radiography systems

Current Amplifiers definition + example

Amplify the current without changing the voltage

fx.: pH meters

Current Amplifiers Types (2)

• Buffer Amplifiers

• Power Amplifiers

Buffer Amplifiers

Amplify current from μA to mA without altering the voltage

A=amper

Power Amplifiers

Amplify current from mA to A

Filters Definition

Amplifiers designed to have specific frequency responses, used to allow or block certain frequency ranges

Types of Filters (8)

• Low-pass Filters

• High-pass Filters

• Band-pass Filters

• Band-stop Filters

• Tuned Filters

• Notch Filters

• Integrating Filters

• Differentiating Filters

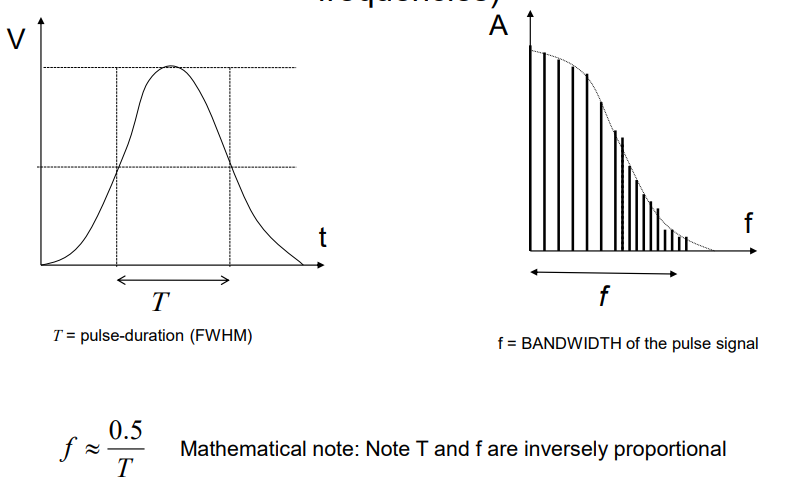
Pulse Signal (4)

• Contains many frequencies in its Fourier spectrum

• Can be represented as a combination of sine waves with different frequencies

• Each frequency contributes to the overall shape of the pulse signal

• Has a bandwidth of frequencies that define its frequency range

Power Gain of an Amplifier Formula

Power Gain (in dB) = 20 × log (Gain)

dB = decibels
Gain = amplification factor of the signal