Calculus (Year 12)

When is a function increasing, decreasing or stationary?

Increasing when f’(x) > 0

Decreasing when f’(x) < 0

Stationary when f’(x) = 0

Concavity?

Concave up when f’’(x) > 0

Concave down when f’’(x) < 0

Possible Point Of Inflection when f’’(x) = 0 (Test)

Maximum vs Minimum

If f’(x) = 0 and…

f’’(x) > 0 Then it is a minimum

f’’(x) < 0 Then it is a maximum

f’’(x) = 0 Then you need to test further

Horizontal vs Vertical POI?

Horizontal POI when… f’(x) = 0 and f’’(x) = 0

Vertical POI when… f’(x) = not zero and f’’(x) = 0

Remember to test.

To find global maximum and global minimum…

• Evaluate critical points (f’(x) = 0 or undefined) (Usually test stationary points)

• Evaluate end points (when a closed domain is present)

Largest is global maximum
Smallest is global minimum

Applications of maximisation and minimisation to solve real life problems…

1. Define the variables

• Identify the quantities involved and assign variables (e.g. area, volume, cost, profit).

2. Write the equation to optimise

• This is the function you want to maximise or minimise (e.g. area, surface area, cost, volume).

3. Find constraints

• Use additional information to express the function in one variable.

4. Differentiate

• Find the derivative of the function.

5. Find critical points

• Solve f′(x)=0f'(x) = 0f′(x)=0 to find potential maxima or minima.

6. Test for max or min

• Use the second derivative test or sign change in f′(x)f'(x)f′(x) to confirm whether it's a max or min.

7. Answer the question

• State the final answer clearly in context (include units).

Primitive Functions

You’re finding a function whose derivative is the original function. 

If the primitive of f(x) is F(x), then F’(x) is f(x).

Reverse the process of differentiation.

F(x) = (xⁿ⁺¹)/(n+1) + C

Link between Primitive Functions and Integration.

Primitive Function of f(x)

= ∫ f(x) dx

Finding area using integration.

1. a∫b f(x) dx

Means you are finding primitive of f(x) which is F(x).

2. Sub a and b into F(b) - F(a)

This is how you find the area from a to b.

Remember:

• No need for c as it will cancel out.

• Absolute value for anything under the curve.

If the question does not ask for area…

Calculate definite integral as is without taking any absolute values

If you are asked to find the indefinite integral…

It will not have a and b.

Make sure to add c!

Area between two curves…

1. Function on top minus function on bottom.

2. Use points of intersection for a and b.

3. Work it out as the area under the top minus the area under the bottom function.

Remember, for area between two curves, top - bottom already handles what is above/below correctly.

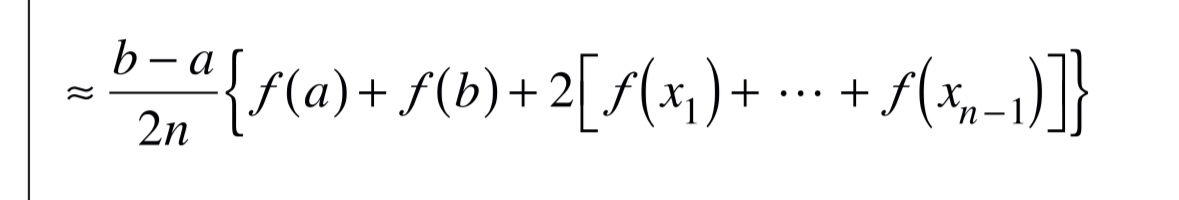
Trapezoidal Rule

Concepts Of Understanding:

b = x value of second end point.

a = x value of first end point.

n = number of sub intervals (remember that five points means four sub intervals).

f(…) = y values of points, thus why in the tables you get x and f(x) as it is like a graph. So if you have the shape, it is values of vertical lengths.

h = width of the individual sub interval. Formula on sheet already accounts for h/2 as h = 0.5 hrs b - a / n

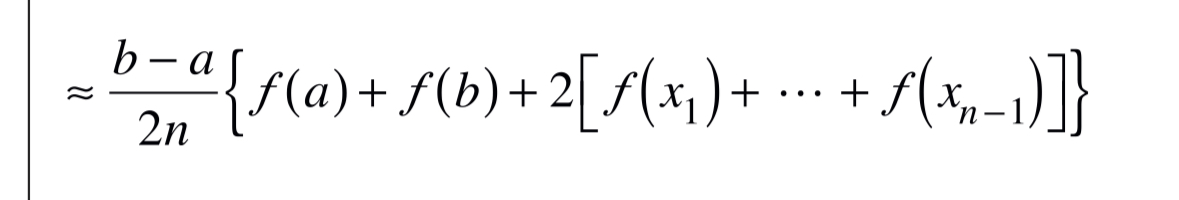
Compound Regions Summary

If curve is above x axis, integrate directly.

If curve is below x axis, use absolute value or split.

If between two curves, subtract bottom from top.

If curves switch order, split at intersection point.

If piecewise, do each piece separately.