Chapter 5 flashcards

What is the equation for an exponential function?

what is f(x)= b^x

What is the “b” term of f(x)=b^x

What is the base of the function

what is the “x” term of f(x)=b^x?

What is the exponent?

Do exponential functions have an x-intercept?

No.

What is the asymptote of this?

The x-axis, it is reaching but will never touch the x-axis

What does the blue line represent?

An increasing function, b>1

What does the purple line represent ?

A decreasing function, 0<b<1.

If the graph of y=b^x has been shifted up or down, what happens with the horizontal asymptote?

It will shift up or down accordingly, reflecting the new position of the graph.

From the graph y=2^x → 2^x +3, what happens with the horizontal asymptote?

The horizontal asymptote will shift up to y=3.

Again, what us ab exponential growth function?

An exponential growth function is a mathematical expression of the form y = a(b^x) where a > 0 and b > 1, indicating that the value of y increases rapidly as x increases.

What is the y-intercept of an exponential growth function?

Whatever the a value is.

What is the horizontal asymptote of an exponential growth function?

The x-axis with the line y=0

What is the equation for a future value of investment that compounds interest annually?

What is S=P(1+r)^t

What are exponential decay functions?

y=a(b^kx), where b is less than 1

What is the equation of a future value of investments that compounds interest continuously?

S=Pe^rt

This is the logarithmic form

What is logb(a)=c?

This is the exponential form

What is b^c=a?

Log2(8)=3 into Exponential

This means 2^3=8.

Log5(25)=2 into exponential

5²=25

Log3(81)=4 into exponential

3^4=81

Log10(1000)=3 into exponential

10^3=1000

2³=8 into Log form

Log2(8)=3

3^4=81 into a log

Log3(81)=4

7²=49 into a log

Log7(49)=2

y=log(b)x: when b>1 . . .

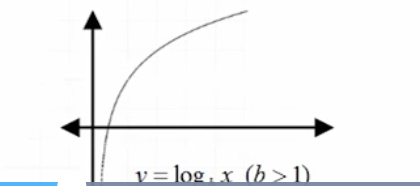
y=log(b)x : when (0<b<1)

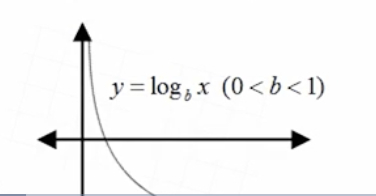
3^-2=1/9 into a log

Log3(1/9)=-2

Log2(32)=5 into

2^5=32

The () and = have a

Relationship when converting between exponential and logarithmic forms.

What is the base of this log: Log(10,000)?

The base of the logarithm is 10, indicating that 10 is raised to a power to yield 10,000.

Log10(10,000)=x into exponential and solve

10^x = 10,000

x=4

This is a logarithm function with base e

and is known as the natural logarithm, often represented as ln(x).

basic properties of logs: when logb(B)=

1

Basic properties of logs: when logb(1)=

0

Basic properties of logs: when logb(b)^x=

x

Basic properties of logs: when M and N are the same then.

logb(M) = logb(N)

What is the product property of logs

logb(MN) = logb(M) + logb(N)

what is the quotient property of logs?

logb(M/N) = logb(M) - logb(N)

What is the power property of logs?

logb(M)^k= klogb(M)

This is the change of base formula:

loga(x)= logb(x) / logb(a)

Solve 5=2^x

1st) log(5)=log(2)^x

• log5= xlog(2)

• 2nd) x = log(5) / log(2)

x= log5/logs2 (evaluate)

Solve log2(x)=-5

• 2^-5=x

• x=1/2^5= 1/32

What is the equation for an exponential growth function?

y=a(1+r)²

What is the equation for an exponential decay function?

y=a(1-r)²

Compounded annually means . . .

Interest that is added to an account at the end of each year

What is the equation for finding future value of an investment that is compounded annually?

S=P(1+r)^t

If $1000 is invested at 5% interest compounded annually for 7 years, what is the future value of investment?

S=1000(1+.05)^7= $1407.10

What is the equation for finding the future value of an investment with periodic compounding?

S=P(1+r/k)^kt

where k is the number of compounding periods per year.

What is the equation for finding the future value of an investment with continuous compounding?

S=Pe^rt

If $1000 is invested at 5% interest compounded continuously for 7 years, what is the future value of the investment?

S=1000e^(.05)(7)= 1419.07

What is the equation for finding the present value

P=s(1+i)^-n

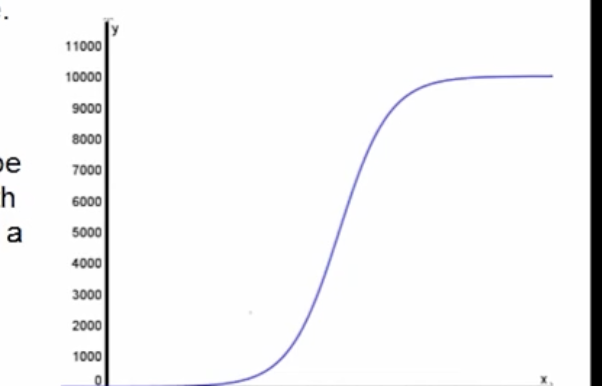
These are functions that grow slowly, increase at a rapid rate, and finally slow over time to a rate that is almost zero. “S-shaped curve”

What are logistic functions?

What is the equation of a logistic function?

what is f(x)= c/1+ae^-bx?

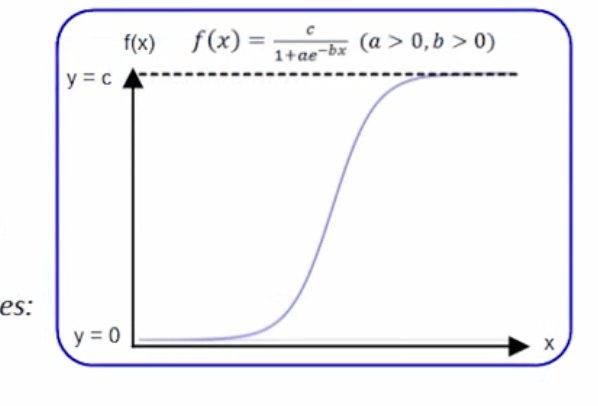
What are logistic growth functions?

a>0 and b>0

• Horizontal asymptote: y=c

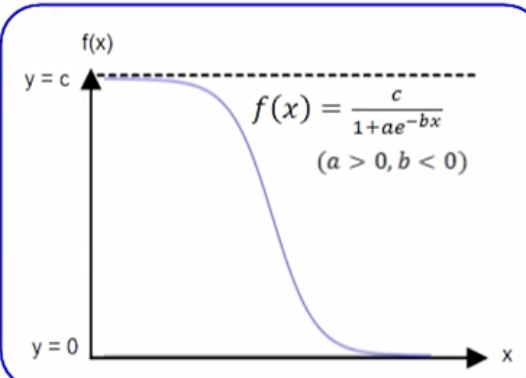
What are logistic decay functions?

a>0 but b<0

This are a type of function that models rapid growth and eventually levels off, describing human growth and the development of growth of organizations

What are Gompertz functions ?

What is the equation of a Gompertz function?

N=Ca^R^t

• t= time

• R= rate of growth

• maximum possible number of individuals

• a= proportion of C