Indeterminate and none-indeterminate forms + Other stuff I kept forgetting

When do you apply L’Hopital?

For indeterminate forms

0-∞

not indeterminate

∞+∞

not indeterminate

0×1

not indeterminate

∞^∞

not indeterminate

∞/∞

indeterminate

0/0

indeterminate

∞^0

indeterminate

1^∞

indeterminate

0*∞

indeterminate

0^0

indeterminate

0/∞

not indeterminate

∞+∞

not indeterminate

∞-∞

indeterminate

1*∞

not indeterminate

How do you find the inflection points?

f”(x)=0

f(x) is continuous on the closed interval [a,b] then…

it’s differentiable on (a,b) and integrable on [a,b]

Cube

Volume: s³ Surface Area: 6s²

Rectangle Prism + Rectangle

Volume: LWH Surface Area: 2LH+2LW+2WH

A: LW Perimeter: 2(L+W)

Cone

Volume: 1/3π r²h

Surface Area: πr(r+√h²+r²)

Triangular Prism

Volume: BH Surface Area: 2HB+B²

Triangle

Area: ½BH

Cylinder

Volume: πr²h Surface Area: 2πrH+2πr²

Sphere

Volume: 4/3 πr³
Surface Area: 4πr³

f’(x)=cosx

-sinx

f’(x)=sinx

cosx

f’(x)=tanx

sec²x

f’(x)=cot

-csc²x

f’(x)=secx

secxtanx

f’(x)=cscx

-cscxcotx

d/dx(arcsinx)

1/√(1-x²)

d/dx(arccosx)

-1/√1-x²

d/dx(arctanx)

1/(1+x²)

d/dx(arccotx)

-1/(1+x²)

d/dx(arcsecx)

1/(|x|√x²-1)

d/dx(arccscx)

-1/(|x|√1-x²)

turn tan(x) into

sin(x)/cos(x)

f(x)=x³ (-inf,inf)

no abs. max/min

f(x)=1/x²+1 (-inf,inf)

abs max no abs mini

f(x)=tan(x) (-pi/2,pi/2)

no abs max/min

Extreme Value Theorem

f is continous [a,b], there is a point within it that has an abs max and abs min

Fermat’s Theorem

If f has a local extremum at c and f differentiable at c means f’©=0 or f’©=Undef

Local extrema at f’©=Undef

-abs value x

-cusp

semi circle

Area: πr²/2

Perimeter: πr+2r

No local extrema at f’©=0

x³ with f’©=0 being horizontal

No local extrema at f’©=Undefined

∛x f’©=Undef horizontal

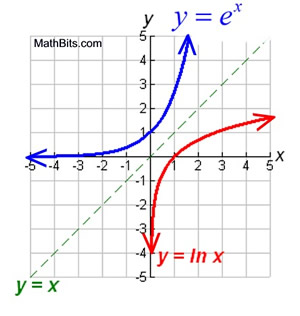
What’s this

ln(x) and e^x function graph

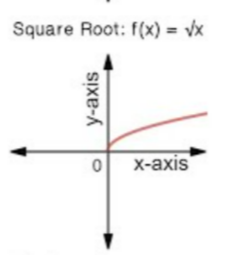
What’s this

f(x)=√x sq root function graph

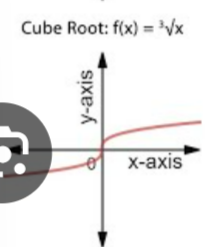
What’s this

f(x)=∛x cube root function graph

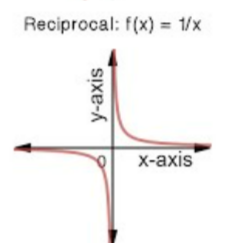
What’s this

f(x)=1/x reciprocal function graph

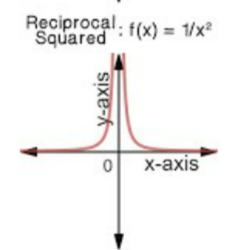
What’s this

f(x)=1/x² rational function graph

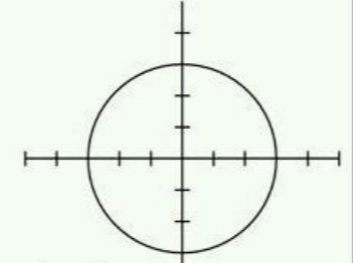
Graph equation for a circle

x²+y²=r²