Cycle 5

Scalar

Quantity with only magnitude

Vector

Quantities that have both magnitude and direction

Weight

Vector Quantity

Weight is sometimes used as a synonym for force. Your weight, in Newtons, is your mass, in kilograms, multiplied by the acceleration due to gravity, which is 9.8m/s~ downward on Earth. Although your mass remains constant, your weight would be different on another planet because gravity is different on other planets.

Fg = mg

Geometric vector

Directed line segment

Tail (initial point)

Head (terminal point)

Direction is from head to tail

Equivalent vectors

have the same length/magnitude and the same direction

Opposite Vectors

Vectors with the same magnitude, but opposite directions

Quadrant Bearings

compass measurements between 0° and 90° east or west of the north-south line. (Always start at N or S)

True Bearings

are compass measurements between 0° and 360° beginning at the north and rotating clockwise.

Resultant

add two or more vectors, you are finding a single vector

Adding Same Direction Parallel

Vectors a and b are parallel and have the same direction

Place vectors tip to tail and add, the direction of resultant will be the same as original vectors

Adding Opposite Direction Parallel Vectors

Vectors c and d are parallel but are in opposite directions.

Place tail of d and head of c

Resultant is same direction as c

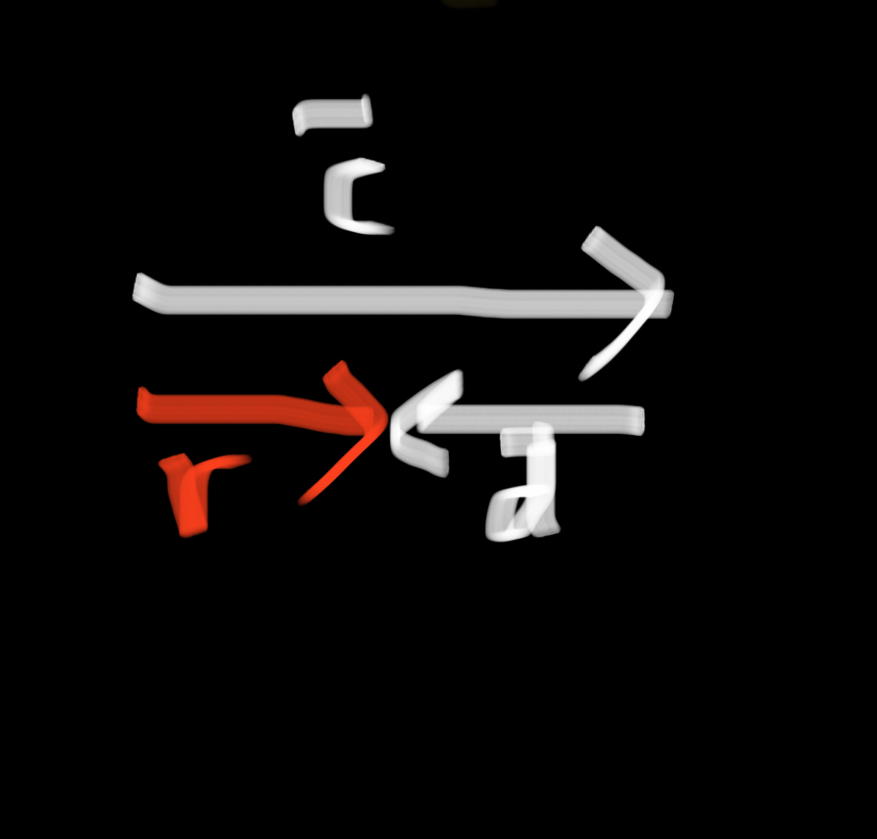
Subtracting parallel vectors

The relationship between addition and subtraction with vectors is similar to the relationship between addition and subtraction with scalars. To subtract u - v, add the opposite of v to u.

In other words, i - vis equivalent tou + (-v).

The Zero Vector

• When you add two opposite integers, the result is zero. A similar result occurs when you add two opposite vectors.

• The zero vector is written as 0 (with vector sign) It has no specific direction.

Multiply Vector by a Scalar

The magnitude is multiplied by the scalar and the vectors are parallel

k > 0

kv has the same direction as v

k < 0

kv has the opposite direction of v

Distributive Property

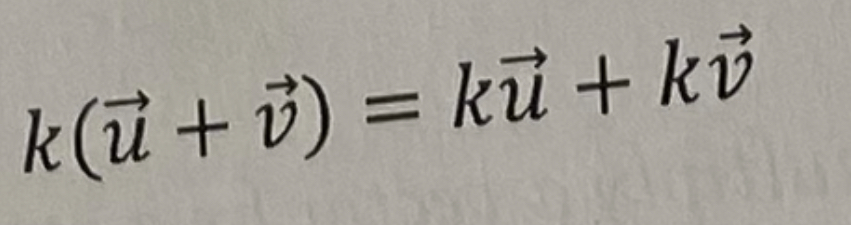
Associative Property

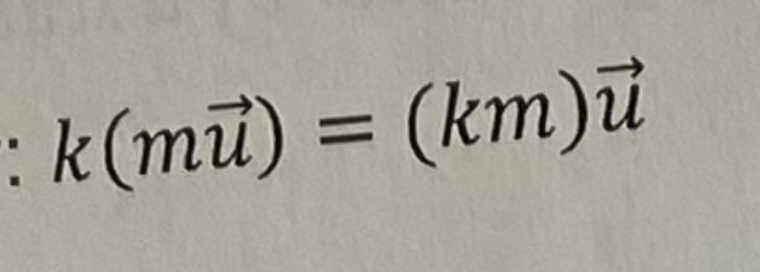
Identity Property

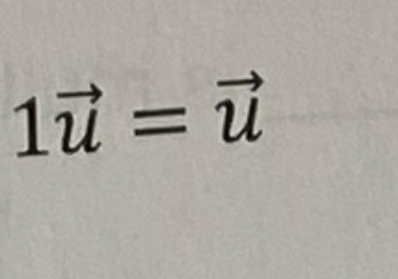
Collinear Vector

If they lie on a straight line when arranged tail to tail.

• Are scalar multiples of another, which means they are parallel