Triple box method and Identity.

Short flashcards about basic triple box method, algebraic proof and identity

An identity is an equation that is ____ for ___ values of variables in the equation. Basically you are proving the left side is equal to the right side.

true,ALL,

If both sides match you would say…

There is an identity

If both sides do not match you would say…

There is no identity

What is algebraic proof?

The steps or arguments behind an algebraic solution. Basically your work.

How would you use the box method on a polynomial with 5 or more terms?

By adding an extra row or column as seen here:

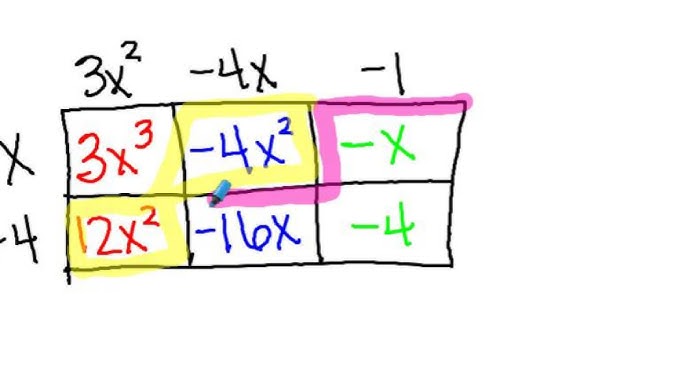
Verify if this is correct:

(3x+2)(3x-2)=9ײ-4

true

9ײ-4=9ײ-4

Rewrite the following in standard form:

(x+y)³

x³3yx²+3xy²+y³

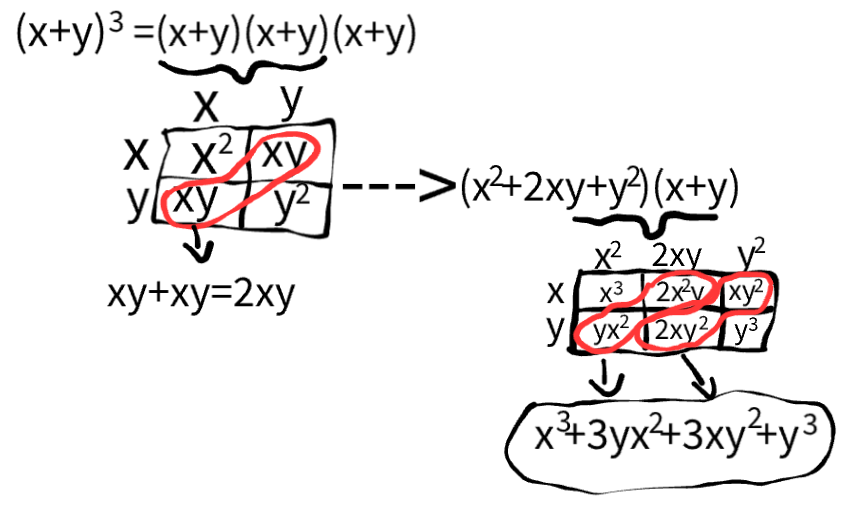
Remember: Variables always have a _____ ___ next to them

Invisible 1 or number

When adding/combining like terms using the box method (not multiplying) you do not ______

do not add exponents or variables

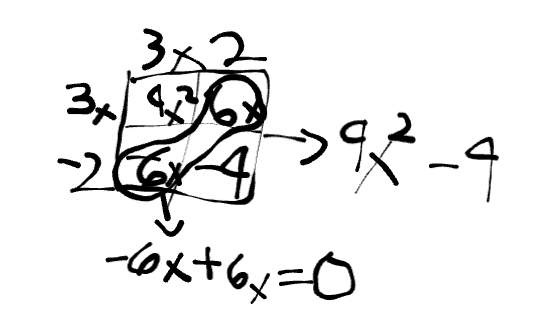
Confirm if the following is true:

(a+b)(a²-ab+b²)=a³+b³

There is an identity

a³+b³=a³+b³

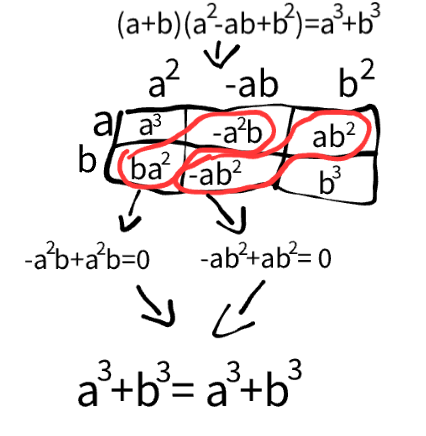
Rewrite the following in standard form:

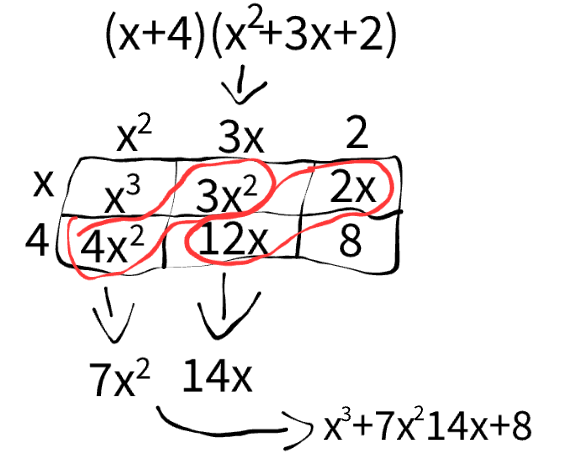
(x+4)(x²+3x+2)

x³+7ײ+14+8