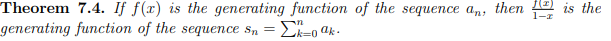Discrete Mathematics- Propositions and Principles

Proposition 1.1. Let X and Y be finite sets. What is :

(a) |X × Y | =

(b) |X^n | =

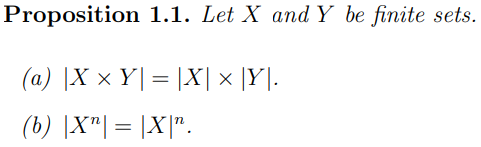
What is an Arrangement and what is meant by its length?

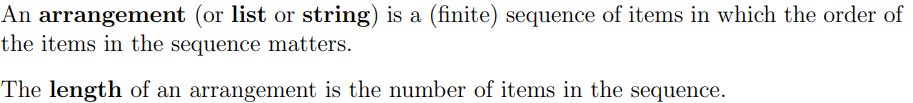
What is STANDARD PROBLEM #1?

What is STANDARD PROBLEM #2?

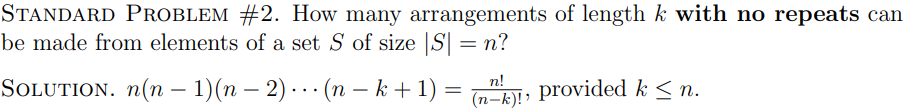
What is the multiplication problem?

What is a permutation?

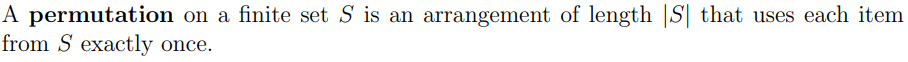
What is proposition 2.1?

If |S| = n, how many permutations are there?

What is the Permute function?

What is the addition principle?

What is the meaning of “or” in a statement- What principle can we use?

What is a combination?

What do the multiplicities mean for an element in regards to combinations?

What does the size of a combination mean?

What is Standard Problem #3?

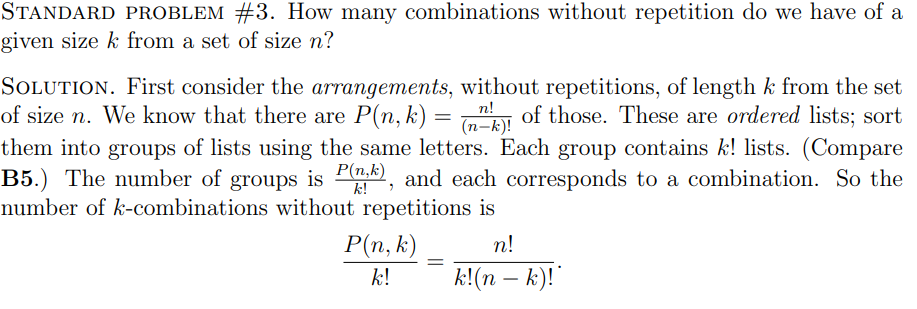
What is Proposition 3.1.? n choose k is the same as n choose …

What is Pascal’s formula (Proposition 3.2)?

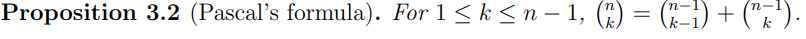
What is the binomial theorem? (Theorem 3.3)

What is STANDARD PROBLEM #4?

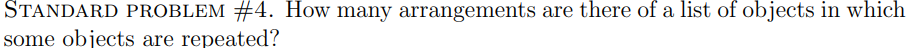
What is theorem 4.1?

Given a list of n objects of r different types, in which objects of type i occur ni times (with n1 + · · · + nr = n), the number of arrangements of the list is

What is STANDARD PROBLEM #5?

What is STANDARD PROBLEM #5?

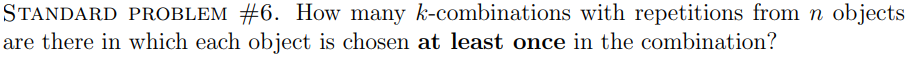
What is the number of k-combinations from n different objects with repetition and each object occurring at least once (Theorem 4.2)?

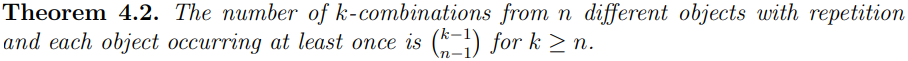
What is the choose formula associated with SP#5

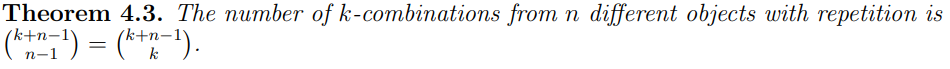
What is the choose formula associated with SP#6

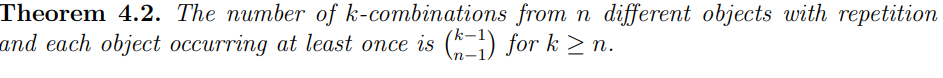
What is extended definition of the choose function for real numbers/Macluarin’s theorem?

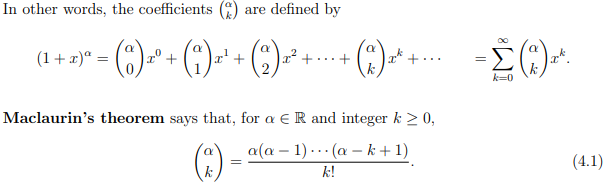
What are the different cases for alpha in the extended binomial theorem.

What is the principle of upper negation (Proposition 4.4)?

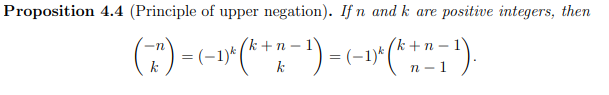
What is 1/(1+x)^n as a power series?

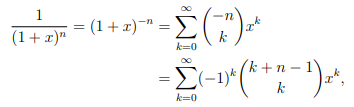
What is 1/(1-y)^n as a power series?

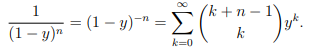
What is the principle of mathematical induction?

What is the pigeon-hole principle?

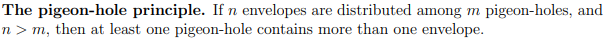
What is the inclusion-exclusion principle?

Consult notes for example

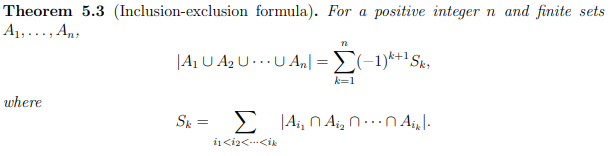
What is the union of three sets equal to (Proposition 5.2)

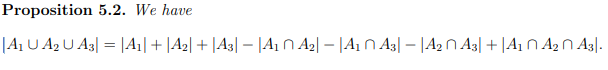
What is the formula for the number of derangements?

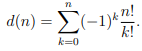
What is the general method for solving linear homogenous recurrence relations?

seek solutions of the form a_n = xⁿ

When solving linear homogenous recurrence relations, what do you do if repeated roots occur?

How to solve inhomogeneous linear recurrence relations?

When solving linear homogenous recurrence relations, how do you determine the particular solution?

When solving linear homogenous recurrence relations, what adjustments may need to be made to the particular solutions?

what is the generating function for a sequence?

What is Lemma 7.1? the useful results for generating functions?

What are the different forms of generating functions?

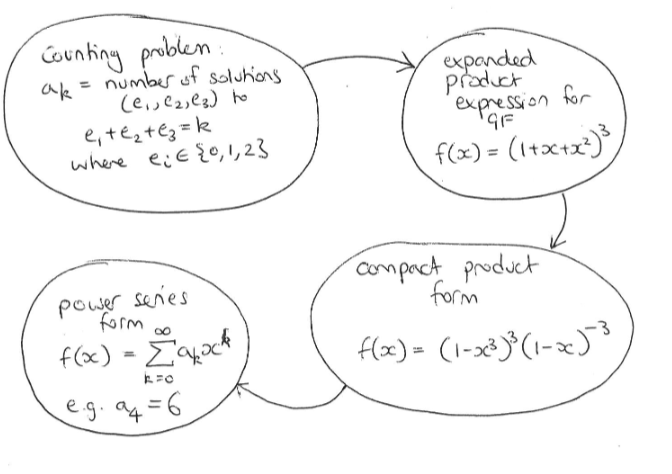
How are generating functions used to solve recurrence relations?

What is a partition of a positive integer n

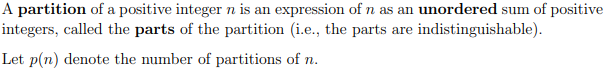
What is the number of partitions p(n) of n in product and series notation?

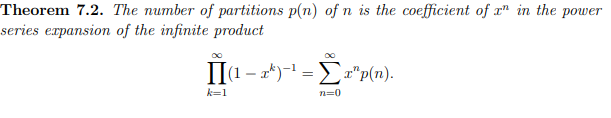
If a_n is a sequence with generating function f(x) , then the generating function for the sequence b_n = na_n is?

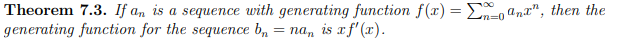
What is the sum of all terms in a_n