APPC Exam Review

The a in g(x)=af (b(x±h))±k

Vertical dilation by a factor of |a|

Reflection over x-axis if a <0

The h in g(x)=af (b(x±h))±k

Horizontal translation

Left when x+h, Right when x-h

The k in g(x)=af (b(x±h))±k

Vertical translation

Up when k > 0, down when k<0

The b in g(x)=af (b(x±h))±k

Horizontal dilation by a factor of

Reflection over y-axis if b<0

Average Rate of Change between (a, f (a)) and (b,f(b))

f(b)-f(a)

---

b-a

Where is a function positive/negative?

• Positive-when the y-coordinates are above the x-axis

• Negative - when the y-coordinates are below the x-axis

What defines an increasing/decreasing function?

• Increasing when the outputs increase as the inputs increase

• Decreasing when the outputs decrease as the inputs increase

What is a Point of Inflection?

The ordered pair where concavity changes

What justifies an increasing rate of change?

When a function is concave up

What justifies a decreasing rate of change?

When a function is concave down

What does it mean if c is odd in f(x)=a(x-b)?

• c is a zero with odd multiplicity

• The graph of ƒ will cross the x-axis at x=c

What does it mean if c is even in f(x)=a(x-b)?

• c is a zero with even multiplicity

• The graph of f will touch the x-axis and turn at x=c

What is an even function?

• When f(x)=√(x)

• Appears symmetric about the y-axis

What is an odd function?

• When f(x)=-f(x)

• Appears symmetric about the origin (rotational)

Notation for end behavior as inputs decrease without bound

Notation for end behavior as inputs increase without bound

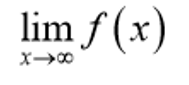
Horizontal asymptote test when

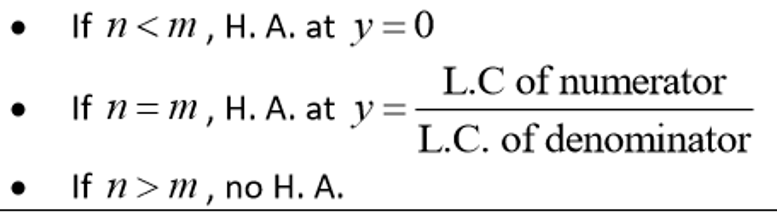
When does a rational function have a slant asymptote?

• When the degree of the poly in the numerator is exactly one more than the degree of the poly in the denominator

• Use long division to find

Where does a rational function have a hole?

• When a factor cancels in numerator and denominator (unless if covered by a V. A.)

• Example at x = a in

  r(x)= (x-a)/(x-a)(x-b)

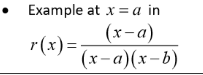
Where does a rational function have a vertical asymptote?

• When a factor is a zero of the denominator after canceling

• Example x = b in r(x)= (x-a)/(x-a)(x-b)

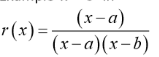
Standard form of an arithmetic sequence

Standard form of a geometric sequence

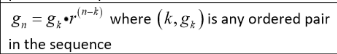
Exponential decay in y=ab^x

• When 0<|b|<1

• • As the inputs increase, the outputs are moving toward the x-axis

Exponential growth in y=ab^x

• When |b|>1

• As the inputs increase, the outputs are moving away from the x-axis

 log_ax + log_ay =

log_a(xy)

nlog_ax =

log_axⁿ

log_ax - log_ay =

log_a(x/y)

log_ax

---

log_ay

log_yx

Pythagorean Trig Identity

sin²x + cos²x = 1

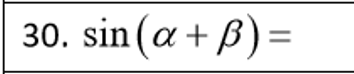
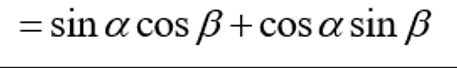
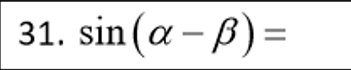
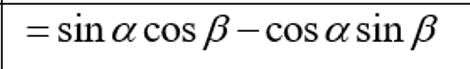
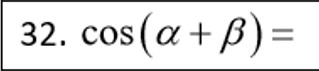
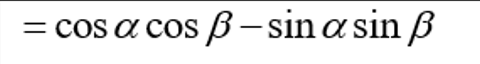
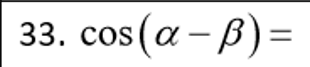
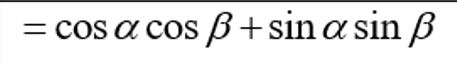
Vertical asymptotes of f(x) = asecbx + d

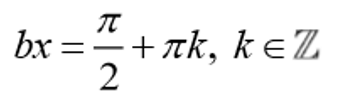
Vertical asymptotes of f(x)= a csc bx+d

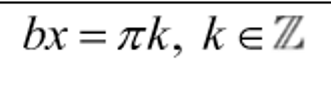
Vertical asymptotes of f(x)= a cot bx+d

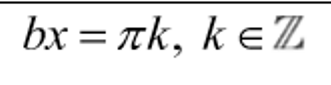
Vertical asymptotes of f(x)= a tan bx+d

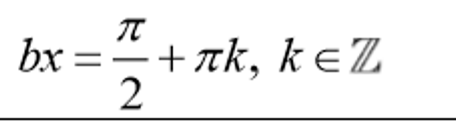
Period of y = a*sin(b(x+c))±d

or y = a*cos(b(x+c))±d

2π/b

Period of y = a*tan (b(x+c))±d

or y=a cot (b(x+c))±d

π/b

How to convert (r,θ)→(x, y)?

x = rcosθ

y = rsinθ

How to convert (x,y)→(r,θ)

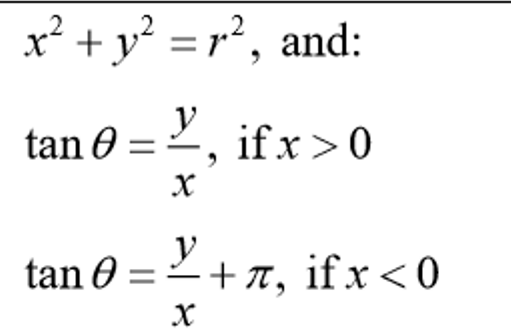
How to convert a + bi to

(rcosθ)+i(rsinθ)

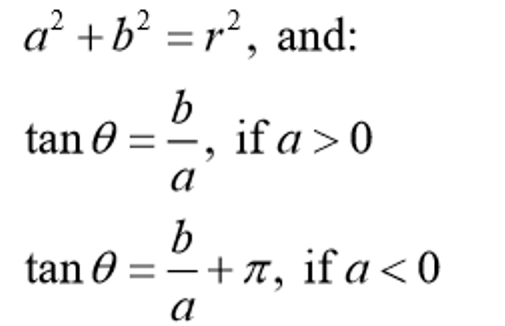
Arc length

θ*r

Range of y = sin^-1x

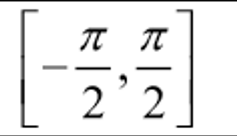
Range of y = cos^-1x

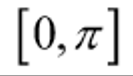
Range of y = tan^-1x

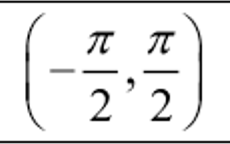
In a polar function, when is the distance from the origin increasing?

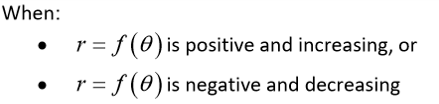
In a polar function, when is the distance from the origin decreasing?

What is error?

• Predicted Value (from regression) - Actual Value

  or

• The opposite sign of the residual

Compare period vs. frequency in a trig function

• Period is the length required for one full cycle of outputs

• Frequency is the reciprocal of period

• Frequency is how many cycles per unit of time

What type of function has constant first differences over equal-length inputs?

A linear function

What type of function has constant rate of change in first differences over equal-length inputs?

A quadratic function

What type of function has constant third differences over equal-length inputs?

A cubic function

What type of function has proportional outputs over equal-length inputs?

An exponential function

What type of function has proportional inputs over equal-length outputs?

A logarithmic function