Physical Sciences Midterm Exam

UofW

What is e (calculus), i (linear algebra), and π (geometry)?

e = 2.17 → the base of the natural logarithms

i = √-1 → the fundamental imaginary number

π = 3.14 → a significant irrational number

What is Euler’s Equation?

• eiπ + 1 = 0

  • Incorporates elements of calculus, linear algebra, and geometry

  • If you multiply a particular irrational number by itself a particular imaginary number of times, then add 1, you get nothing

  • Very important in quantum physics

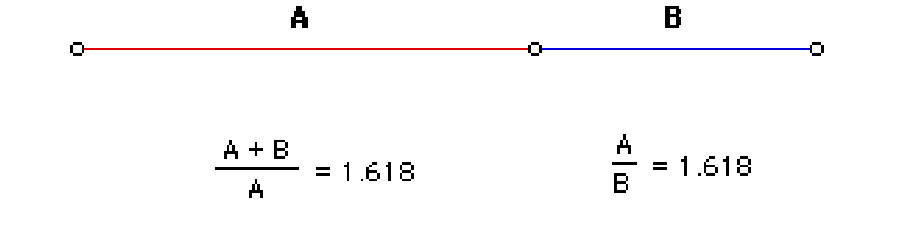
What is The Divine Proportion?

• A.k.a. the Golden Ratio, Phi Φ

• Φ is defined to the ratio obtained by dividing a line segment into two unequal pieces such that the entire segment is to the longer piece as the longer piece is to the shorter

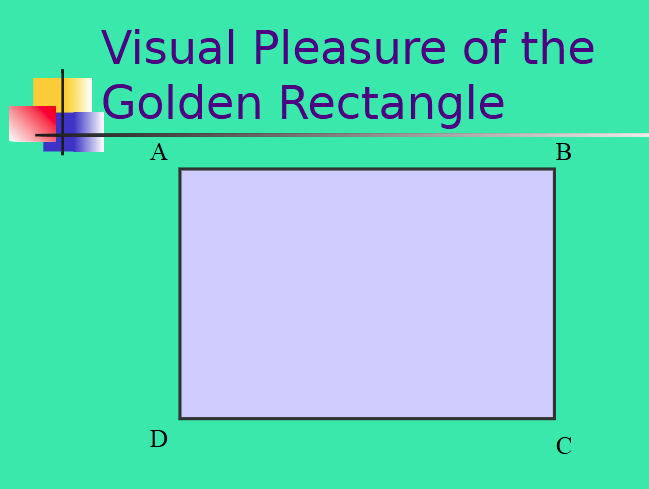
What are the properties of a Golden Rectangle?

• If one chops off the largest possible square from a Golden Rectangle, one gets a smaller Golden Rectangle.

• If one constructs a square on the longer side of a Golden Rectangle, one gets a larger Golden Rectangle.

• Both constructions can go on forever.

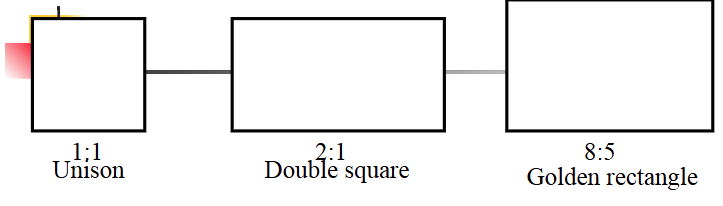
How does the Golden Ratio relate to music?

• The three most pleasing musical intervals are unison, the octave, and the major sixth

• The ratio of frequencies of these intervals is 1:1, 2:1, and 8:5.

• These ratios correspond to a square, a rectangle, and a golden rectangle.

• The major sixth is proven to be the most pleasurable music interval of all.

What are Fibonacci Numbers?

• Fibonacci Equation → un+1= un+un-1

• In the Fibonacci Sequence, each term is the sum of the two previous terms

• When a number from the Fibonacci sequence is divided by the number that precedes it, the quotient is approximately equivalent to the golden ratio

• As higher terms are divided, the quotient comes closer and closer to the exact value of the golden ratio

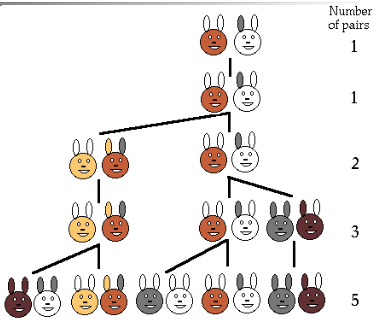
What are Fibonacci’s Rabbits?

• The original problem that Fibonacci investigated in 1202

• How fast rabbits could breed in ideal circumstances

What are some examples of Fibonacci in nature?

• All follow the growth pattern of the Golden Spiral.

  • The seeds of a sunflower

  • The bracts of a pine cone

  • The seashell of the Nautilus pompilius

  • Sneezewort plant

What are man-made examples of the golden ratio?

• The Pyramids

• The Parthenon

• Cathedral of Notre Dame

• Michelangelo’s Holy Family

• Da Vinci’s Mona Lisa

How does SHM work?

• A mass on a spring has a displacement as a function of time that is a sine or cosine curve

• Motion continues indefinitely. Only conservative forces act, so the mechanical energy is constant

What is the Molecular Model of SHM?

• If the atoms in the molecule do not move too far, the force between them can be modeled as if there were springs between the atoms

• The potential energy acts similar to that of the SHM oscillator

What are Damped Oscillations?

• Dissipative forces (friction, air resistance, etc.) remove energy from the oscillator, and the amplitude decrease with time.

• Frequency depends only on the physical properties of the system, not on the energy, so as the oscillation loses energy, the frequency and period stay the same. Only amplitude decreases.

  • This is important for musical instrument design: vibrating string on guitar should be damped, but not too fast.

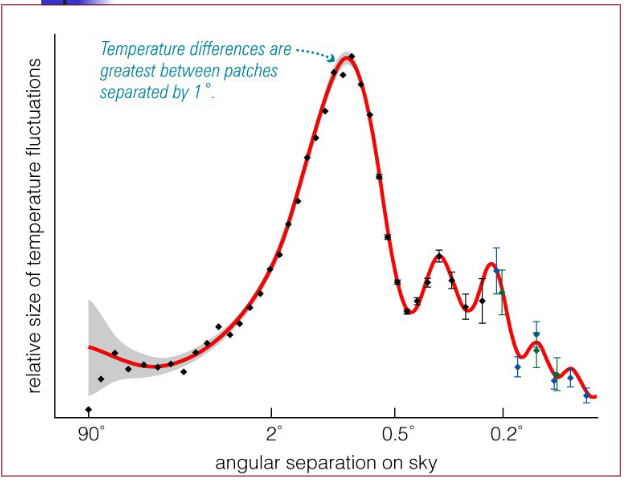
What is Cosmic Background Radiation?

• When cosmologists first looked at the microwave sky, thirty years ago, they noticed it was nearly uniform.

• As observations improved, they detected the dipole anisotropy

What is the Uniformity of CMB?

• Afterglow radiation from the hot Big Bang

• The temperature is extremely uniform all over the sky

• Tiny temperature variations or fluctuations (at the part per million level) can offer great insight into the:

  • Origin, evolution, and content of the universe

  • The origin of galaxies and large scale structures of galaxies

  • Measure the basic parameters of the Big Bang theory

How does CMB relate to SHM?

Observed patterns of structure in universe agree (so far) with the “seeds” that inflation would produce (Sine and Cosine Waves)

What is the Birth of Quantum Mechanics?

• Schrödinger equation is based on the wave equation.

  • This combined with boundary conditions yields various modes of oscillation that depend on integers - just like harmonics of a string

• A resulting beautiful model for the quantization of the energy levels of the hydrogen atom

• A nice analogy to Pythagorean approach - the beauty of nature reflected or matched by simple integral/mathematical models

What is String Theory?

• All matter consists of small one-dimensional objects (strings).

• Strings look like particles when not resolved closely enough

• All particle types are different

• Strings can vibrate in different ways

  • Guitar string

    • Different vibration → Different sound!

  • Fundamental string

    • Different vibration → Different particles!

      • Electron - Photon - Graviton

How old is the Universe?

• The Cosmic Calendar

  • If the entire age of the Universe were one calendar year

  • One month approximately 1 billion real years

    • Jan. 1 - The Big Bang

    • Feb. - Milky Way Forms

    • Sept. 3 - Earth Forms

    • Dec 31, 11:59 - Humans

Where are we in the Universe?

• Address

  • The earth is a planet in the solar system consisting of objects orbiting the star Sun

  • The solar system is part of a galaxy called the Milky Way

  • The Milky Way is a part of a group of galaxies called the Local Group

  • The Local Group belongs to the Local Supercluster (also called Virgo Supercluster).

In what ways do all humans employ scientific thinking?

Scientific thinking is based on everyday ideas of observation and trial-and-error experiments.

• Example: Astronomical observations benefited ancient societies

  • For practical purposes, including agriculture

  • For religious and ceremonial purposes

• Aids to navigation

What are examples of ancient structures and technologies to perform or record astronomical observations?

• Egyptian obelisk

• Stonehenge (England)

• Templo Mayor (Mexico)

• Chankillo (Peru)

• Bighorn Medicine Wheel (Wyoming)

• Polynesian celestial navigation

• French Lunar Phase cave paintings

• Chinese records of supernovas

What is Ancient Greek Science?

• Modern science traces its roots to the Greeks

• Islamic scientists preserved and extended Greek science

  • Our mathematical and scientific heritage originated with the civilisations of the Middle East

Explain the Development of Astronomy

• So far astronomy only involved making observations, recognizing basic patterns and making rudimentary predictions.

• A crucial part of the scientific method - building models/hypotheses that did not resort to supernatural or godly influence - was missing

• This was about to change in Greece…

Why does modern science trace its roots to the Greeks?

• Greeks were the first people known to make models of nature.

• They tried to explain patterns in nature without resorting to myth or the supernatural.

• Thales of Miletus first assumed that the world was understandable and proposed a model of the earth. He successfully predicted a solar eclipse.

Explain Greek Astronomy

500 BC: Pythagoras suggests that the Earth is a sphere, not flat, as had previously been assumed.

240 BC: Eratosthenes measured the Earth

• Compared the angle of the Sun’s rays at noon in two different cities (Syene and Alexandria) and used the distance between them to calculate the planet’s size through geometry.

100-170 AD: Ptolemy and the Ptolemaic model

• Sophisticated geocentric model

• Sufficiently accurate to remain in use for 1,500 years

• Could handle retrograde motion

What observations of the ancient Greek astronomers could you use to prove the spherical model of the Earth to a member of the Flat Earth Society?

Earth as a sphere

• Ships disappear sailing away from shore by sinking below horizon with mast last visible; Earth’s curvature visible over 13 mile distance.

• Circular shadow projected by Earth when it eclipses the Moon

• When traveling north, new stars appeared above northern horizon, while stars previously seen along southern horizon no longer visible; reverse is true traveling south.

How did the Greeks explain planetary motion?

• Heavens must be “perfect”: objects moving on perfect spheres or in perfect circles.

  • But this made it difficult to explain the apparent retrograde motion of planets…

• The modern heliocentric model easily explains apparent retrograde motion

Explain the Ordered Universe

Physical Events

• Predictable, Quantifiable

• Without the predictability of physical events, the scientific method would not be possible.

As seen by:

• Ptolemy (2nd Century)

• Copernicues (16th Century)

• Brahe (Late 16th Century)

• Kepler (Early 17th Century)

• Galileo (Early 17th Century)

Experimentation

• Collecting data using instruments and mathematical calculations

Who was Galileo Galilei?

• Overcame major objections to the Copernican view. Galileo’s experiments showed that objects in the air would stay with a moving Earth.

• Using his telescope, Galileo saw:

  • Sunspots on the Sun (“imperfections”)

  • Mountains and valleys on the Moon (proving it is not a perfect sphere)

• Galileo also saw four moons orbiting Jupiter, proving that not all objects orbit the Earth, and his observations of the phases of Venus proved that it orbits the Sun and not Earth

What is the Nature of Science?

How can we distinguish science from non-science?

• Defining science can be surprisingly difficult.

• Science from the Latin scientia, meaning “knowledge.”

What is the process of the Scientific Method

• Identifying Patterns

• Hypothesis

  • → Theory

  • → Principle (Law)

• Prediction

• Experimentation (Observation)

• This “process” - never truly finished

• Over time, the hypothesis receives more support

• Testing continues

  • Making predictions

  • Observing results

What is an example of the scientific method in every day life?

Realisation/Observation

• Car Won’t Start

Hypothesis

• The battery is dead

Experiment

• See if the radio works

Outcome

• Yes. The battery is okay.

• No. The battery may be dead

What is the idealized scientific method?

• Notice (Identify pattern)

• Ask a question

• Suggest a hypothesis

• Make a prediction

• Perform a test: experiment or additional observation

  • The test does not support the hypothesis: revise the hypothesis or choose a new one.

  • The test supports the hypothesis: make additional predictions and test them.

Does science ever proceed in the idealized way?

• Rarely

  • Sometimes we start by “just looking” then coming up with possible explanations.

  • Sometimes we follow our intuition rather than a particular line of evidence.

What is the first Hallmark of Science?

Modern science seeks explanations for observed phenomena that rely solely on natural causes

• A scientific model cannot include divine intervention

What is the second Hallmark of Science?

Science progresses through the creation and testing of models of nature that explain the observations as simply as possible (Occam’s Razor).

What is the third Hallmark of Science?

A scientific model must make testable predictions about natural phenomena that would force us to revise or abandon the model if the predictions do not agree.

What is a scientific theory?

• The word theory has a different meaning in science than in everyday life.

• In science, a theory is NOT the same as a hypothesis, rather, a scientific theory must:

  • Explain a wide variety of observations with a few simple principles, AND

  • Must be supported by a large, compelling body of evidence.

  • Must NOT have failed any crucial test of its validity.

Darwin’s theory of evolution meets all the criteria of a scientific theory. What does this mean?

• Scientific opinion is about evenly split as to whether evolution happened.

• Scientific opinion runs about 90% in favour of the theory of evolution and about 10% opposed.

• After more than 100 years of putting Darwin’s theory to the test, the theory stands stronger than ever, having successfully met every scientific challenge to its validity.

• There is no longer any doubt that the theory of evolution is true.

What are Systems of Measurement?

• Basis of testing theories in science

• Need to have consistent systems of unites for the measurements

• Uncertainties are inherent

• Need rules for dealing with the uncertainties

What are examples of these Systems of Measurements?

• Standardized systems

  • agreed upon by some authority, usually a governmental body

• SI - Système International

  • agreed to in 1960 by an international committee

  • also called mks for the first letters in the units of the fundamental quantities

What is the SI base unit for length?

Meter (m)

• Defined in terms of a meter - the distance traveled by light in a vacuum during a given time

What is the SI base unit for mass?

Kilogram (kg)

• Past - defined in terms of kilogram, based on a specific cylinder kept at the International Bureau of Standards

What is the SI base unit for time?

Seconds (s)

• Defined in terms of the oscillation of radiation from a caesium atom

What are prefixes?

• Prefixes correspond to powers of 10

• Each prefix has a specific name and abbreviation

Who are some important historical “scientists?”

• Ancient = philosophers

  • Aristotle

• Middle Ages = artists

  • Leonardo da Vinci

• Renaissance = modern science

  • Galileo (Father of experimentation)

What is Aristotle’s Law of Free Fall?

Heavier objects fall faster than lighter ones

What is Galileo’s Law of Free Fall?

• All objects fall at the same speed

  • Galileo showed that g is the same for all falling objects, regardless of their mass.

Explain Galileo and the Leaning Tower of Pisa

• According to a widespread story, Galileo dropped two objects with different weights from the Leaning Tower of Pisa.

• He expected them to fall at the same time.

• The experiment that proved this was done on the Moon, with hammer and a feather

What is Inertia?

• Galileo explained the behavior of matter to stay in motion by inertia.

• Inertia is the tendency of an object to remain in motion in the absence of an unbalanced force such as:

  • friction

  • gravity

What is Motion?

• Speed = Distance over Time

• Velocity - Speed in a specific direction

• Acceleration - rate of change in velocity

What is Force?

• Force is a push or pull on a body

• It usually causes:

  • a distortion in the body,

  • a change in the body’s velocity, or both

• Force is the agent for a change in motion.

• The units of force include:

  • SI: newton (N), dyne or metric ton (2000 N)

  • English: pound (lb), ounce (oz) or ton (2000 lb)

• To convert between SI and English:

  • 1 N = 0.225 lb

  • or 1 lb = 4.45 N

What are Fundamental Forces?

• Types

  • Strong nuclear force

  • Electromagnetic force

  • Weak nuclear force

  • Gravity

• Characteristics

  • All field forces

  • Listed in order of decreasing strength

What are External and Internal Forces?

• External force

  • Any force that results from the interaction between the object and its environment

• Internal forces

  • Forces that originate within the object itself

  • They cannot change the object’s velocity

What is the Empirical ‘Feel’ of Forces?

• We have a direct sensation of the forces that act on our body.

  • As I stand on the floor, I feel my shoes pushing up on my feet. The nerves in the soles of my feet transmit this feeling to my brain.

  • The nerves in our joints also give us a sense of the weight of our bodies.

  • If you stub your toe (or worse) you feel the force against your toe.

What is Newton’s first law of motion?

A moving object will continue moving in a straight line at a constant speed, and a stationary object will remain at rest, unless acted upon by an unbalanced force.

What is Newton’s second law of motion?

When a force F acts on a body of mass m, it produces in it an acceleration a equal to the force divided by the mass.

• Thus, a = F/m, or F = ma.

What is Newton’s third law of motion?

• To every action there is an equal and opposite reaction'

  • The Earth pulls down on you with a force equal to your weight, and you pull “up” on the Earth with a force equal to your weight.

  • You move more than the Earth because the Earth is much more massive than you.

What is Gravity?

An attractive force between any 2 objects in the universe which is proportional to the masses of the objects and inversely proportional to the square of the distance between them.

What is the Law of Universal Gravitation?

• Newton’s Law of Universal Gravitation states that every object exerts a gravitational force on every other object.

• The force increases as either object’s mass increases.

• The force decreases as the objects move farther apart.

• Objects fall due to the force of gravity

• Acceleration is 9.8 m/s2 at the Earth’s surface (1/6 of that value is g on the Moon)

  • It is this force that is the object’s weight

    • w = mg

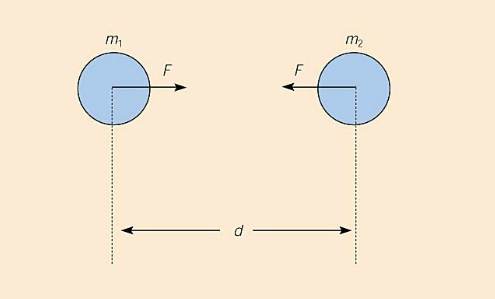
How can we mathematically write the the Law of Universal Gravitation?

• m₁ is the mass of one object

• m₂ is the mass of the other object

• d is the center-to-center distance separating the objects.

Explain acceleration Due to Gravity.

• Objects fall to the Earth with uniformly accelerated motion, caused by the force of gravity.

  • All objects experience this constant acceleration.

  • This acceleration is 9.8 m / s².

  • Gravity acts on objects at all times, regardless of their position.

What is the acceleration of gravity? What is the difference between weight and mass?

• Galileo showed that g is the same for all
  falling objects, regardless of their mass.

  • Weight - force of gravity on an object in a particular place

    • Can Change

  • Mass - amount of actual matter an object has

    • Stays constant

In the Law of Universal Gravitation, specifically gravity, what is the difference between “G” and “g”?

“G” – universal constant, applies to any 2 masses in the universe.

“g” – gravity on the Earth’s surface only.

What is Newton’s Cannon? (Mountain)

• Newton imagined that if a cannonball were given sufficient velocity, the curving away of the earth’s surface beneath it would need to be taken into account in determining its range

  • Newton imagined that if the speed were fast enough, the cannonball would circle the Earth

• Is the moon falling towards the Earth?

  • No, Gravity + Newton’s first law / Cannon

Why are astronauts weightless in space?

• There IS gravity in space... weightlessness is due to a constant state of free-fall:

  • If an object gains enough orbital energy, it may escape (change from a bound to unbound orbit)

  • Escape and orbital velocities don’t depend on the mass of the orbiting object, but on the mass of the Earth

• Escape velocity from Earth ≈ 11 km/s from sea level (about 40,000 km/hr)

What does the universe look like from Earth?

• When you look up at the stars, you look out through a layer of air only about 100 kilometers deep.

• With the naked eye, we can see more than 2,000 stars as well as the Milky Way.

What is the Milky Way?

• Our Galaxy – Milky Way is shaped like a disk.

• Our solar system is in that disk.

• When we look at the Milky Way in the sky, we are looking along that disk.

What are constellations?

• A region of the sky, within official borders set in 1928 by the IAU

• There are 88 official
  constellations.

• Often recognizable by a pattern or grouping of stars called asterisms.

• Some patterns span several constellations.

What were stellar names originally based on?

• Their Brightness

• Their location in the sky

Alpha Centauri and the Sun have about the same luminosity, but which one appears brighter?

The Sun

What is the Celestial Sphere?

• When we look at the sky, we cannot tell how far different stars are from us.

  • Ancient astronomers thought that the sky was a giant celestial sphere onto which all the stars were attached.

  • Although we now know better, the celestial sphere remains useful for describing the location (but not the distance) of stars in the sky.

• Stars at different distances all appear to lie on the celestial sphere.

• The ecliptic is the Sun’s apparent path through the celestial sphere. Why is it tilted from the celestial equator?

What is Angular Size and Angular Distance?

• Since we cannot accurately judge how far objects in the sky are, we CANNOT tell their true size.

• However, we CAN talk about the angular size of an object or the angular distance between two objects.

• Angular size or distance is measured in degrees.

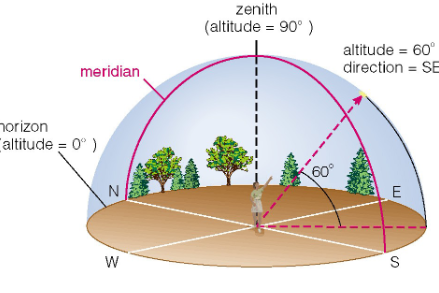
How do we locate objects in the sky?

• 1 - Know your reference points

• 2 - Locate an object by its altitude (above horizon) and direction (along horizon)

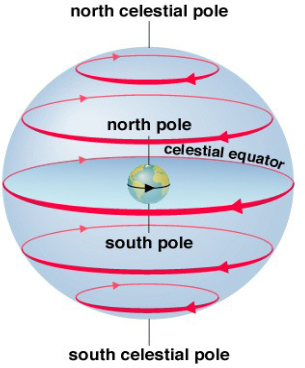
What is the Daily Motion of the Earth?

• As the Earth rotates, the sky appears to us to rotate in the opposite direction.

• The sky appears to rotate around the N (or S) celestial poles.

• If you are standing at the poles, nothing rises or sets.

• If you are standing at the equator, everything rises & sets 90 degrees to the horizon.

Explain the daily motion of objects in the sky

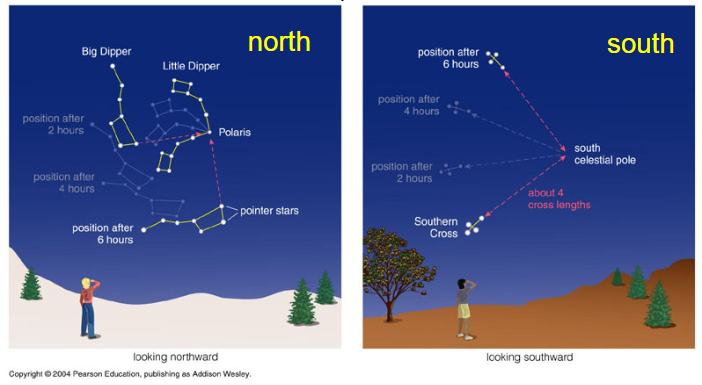
Stars rise and set every night, Earth rotates from west to east so stars appear to circle from east to west.

What is our view from Earth?

• Stars near the north celestial pole are circumpolar and never set.

• We cannot see stars near the south celestial pole.

• All other stars (and Sun, Moon, planets) rise in east and set in west.

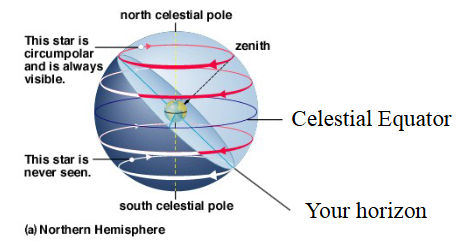
What is the arrow pointing to?

• The Zenith

• The North Celestial Pole

• The Celestial Equator

The North Celestial Pole

How do we specify locations on Earth?

• Latitude

  • position north or south of equator

• Longitude

  • position east or west of prime meridian (runs through Greenwich, England)

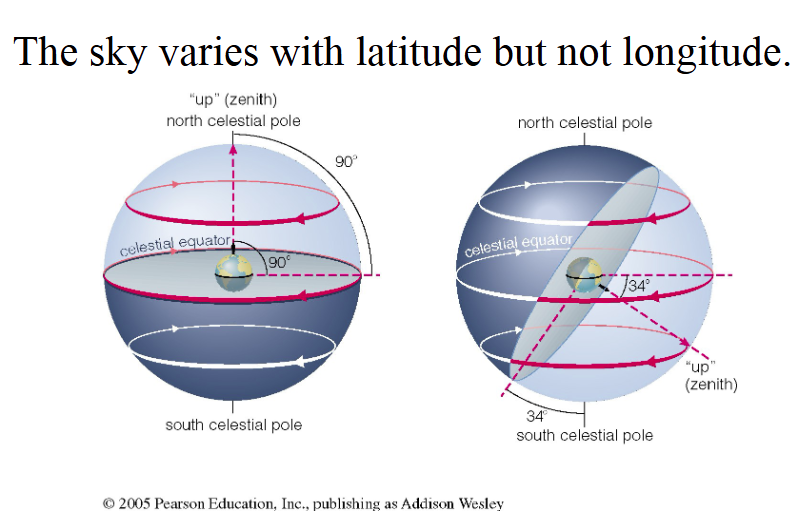
What determines the variation of the night sky (regarding the position of the earth)?

The night sky depends on latitude because your position on Earth determines which constellations remain below the horizon.

The North Star (Polaris) is 50° above your horizon, due north. Where are you?

• You are on the equator.

• You are at the North Pole.

• You are at latitude 50°N.

• You are at longitude 50°E.

• You are at latitude 50°N and longitude 50°E.

• You are on the equator.

• You are at the North Pole.

• You are at latitude 50°N.

• You are at longitude 50°E.

• You are at latitude 50°N and longitude 50°E.

Why don’t we see the same constellations throughout the year?

• Depends on where you travel on Earth

  • Constellations vary with latitude.

• Depends on time of year

  • Constellations vary as Earth orbits the Sun.

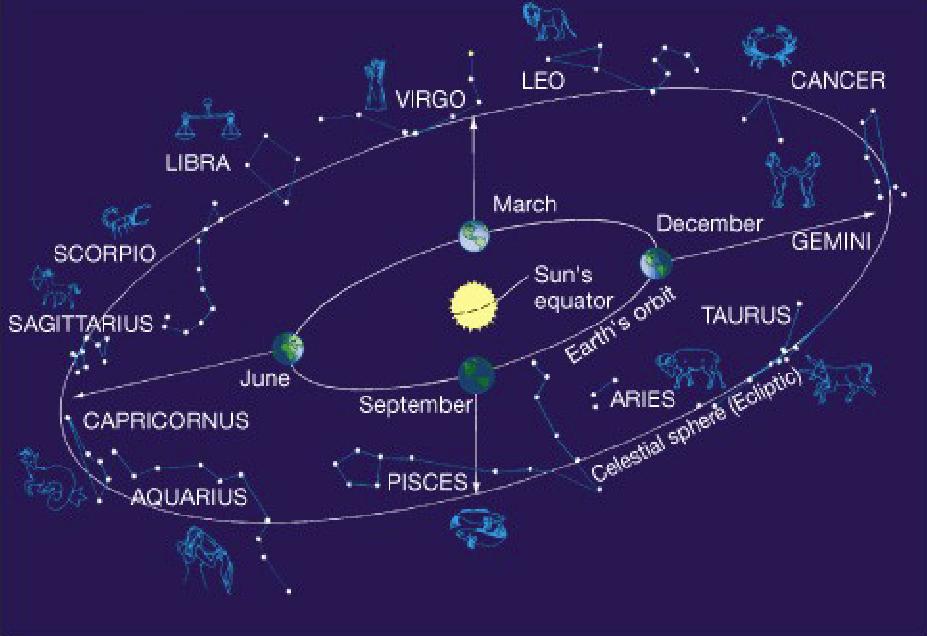
What is the yearly motion of constellations?

• Constellations we see depend on time of year

  • They depend on time of year because Earth’s orbit changes the apparent location of the Sun among the stars.

What is annual motion?

• As the Earth orbits the Sun, the Sun appears to move

  eastward with respect to the stars.

• The Sun circles the celestial sphere once every year.

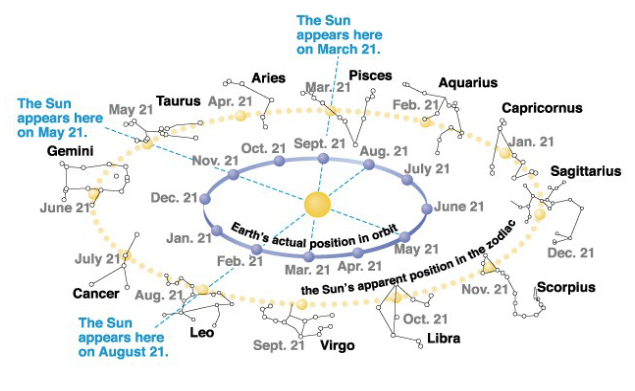
What are the four aspects of Annual Motion?

• Ecliptic

  • The apparent path of the Sun through the sky

• Equinox

  • Where the ecliptic intersects the celestial equator

• Solstice

  • Where the ecliptic is farthest from the celestial equator

• Zodiac

  • The constellations which lie along the ecliptic

Explain the Ecliptic in greater detail

• The apparent path of the Sun, relative to the stars on the celestial sphere, for a year.

• The ecliptic forms a great circle on the celestial sphere, inclined at an angle of 23.5° to the celestial equator.

  • In reality, the plane of the ecliptic is the plane of Earth’s orbit around the Sun.

  • Its tilt is a consequence of the inclination of our planet’s rotation axis to its orbital plane

What causes the seasons?

• Seasons are opposite in the N and S hemispheres, so distance cannot be the reason.

  • The reason for seasons involves Earth’s axis tilt.

• Earth’s orbit is nearly circular, so it is always about the same distance from the Sun.

• Seasons depend on the orbit (revolution) of the Earth around the Sun and how the tilt of the Earth’s axis affects the directness of sunlight and the length of days

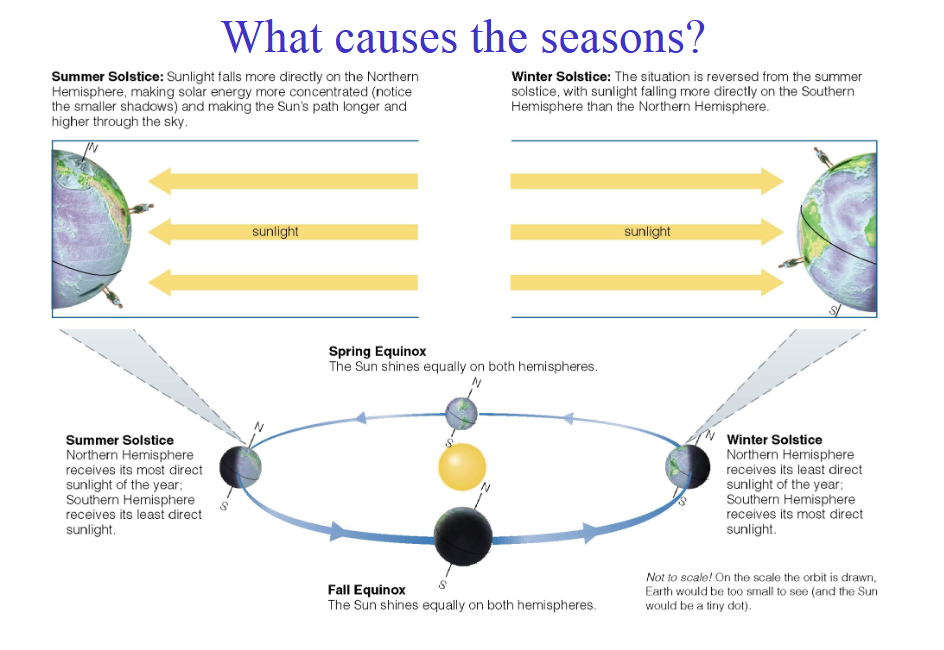
How does the Earth’s tilt cause seasons?

• The tilt of the Earth’s rotation axis relative to the plane of its orbit remains constant, so its orientation relative to the sun changes.

  • This means that for half the year, the Northern Hemisphere is tilted more towards the sun

  • And for the other half of the year, the Southern Hemisphere is tilted more towards the sun.

• The Hemisphere receiving more direct sunlight will

  experience summer, the other Hemisphere, winter.

How do we mark the progression of seasons (four special points)?

• Summer solstice: June 21

• Winter solstice: December 21

• Spring (vernal) equinox: March 21

• Fall (autumnal) equinox: September 22

How does Earth’s explain the length of days?

• On the equinoxes, day and night are roughly of equal length.

• Between the Spring equinox and the Summer solstice, days in the Northern Hemisphere grow longer as it is tilted towards the sun, and this hemisphere gets more energy

• On the summer solstice, places in the Northern Hemisphere have their longest day (vice versa in the Southern Hemisphere).

• Between the Summer solstice and the Fall Equinox, days in the Northern Hemisphere grow shorter as its tilt towards the sun decreases, and hence this hemisphere gets less energy. The opposite is true in the Southern Hemisphere.

How can we recognize solstices and equinoxes by Sun’s path across the sky during high noon?

• Summer solstice:

  • Highest path, rise and set at the most extreme north of due east.

• Winter solstice:

  • Lowest path, rise and set at the most extreme south of due east.

• Equinoxes:

  • The Sun rises precisely due east and sets precisely due west.

What is the Zodiac?

• Because of its relationship to changing seasons, ancient cultures attached great significance to the ecliptic.

  • It marks the centre line of the zodiac (‘circle of animals’), a band of the sky divided into 12 parts, each 30 degrees wide.

  • The signs of the zodiac are no longer of special importance in astronomy.

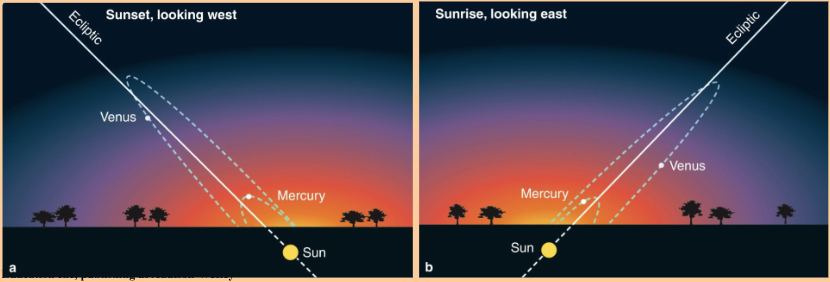
Why are planets seen along the ecliptic, appearing like bright stars?

• As Venus and Mercury orbit inside Earth’s orbit, they never get far from the sun, and are visible in the west after sunset or in the east before sunrise.

• Venus can be very bright, but Mercury is difficult to see near the horizon.

• By tradition, any planet in the sunset sky is called an evening star. Any planet in the dawn sky is called a morning star.

  • Venus seasonally switches from morning to evening star

Does the orientation of Earth’s axis change with time?

• Although the axis seems fixed on human time scales, it precesses over about 26,000 years.

• Þ Polaris won’t always be the North Star.

• Þ Positions of equinoxes shift around orbit; e.g., spring equinox, once in Aries, is now in Pisces!

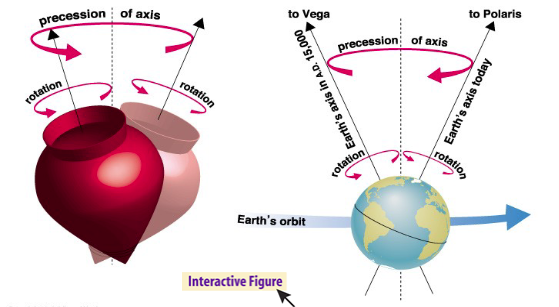
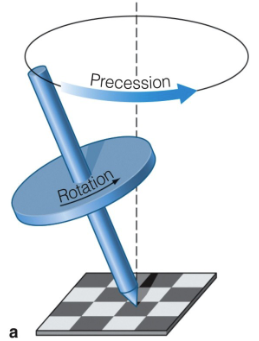
What is precession of Earth’s axis?

• Precession may affect the severity of the different

  seasons and may cause extreme climate changes

  such as ice ages

• Earth’s axis precesses like the axis of a spinning top

What is the Moon?

• The Moon is the Earth's faithful follower.

• It is the object closest to the Earth at about 380k km.

• It orbits the Earth once every 27.32 days.

• It accompanies the Earth on its orbit around the sun.

What is the motion of the moon?

Due to the Earth's rotation from west to east, the Moon, like the stars, appears to rise in the east and set in the west every night. The moon orbits eastwards around Earth once a month.

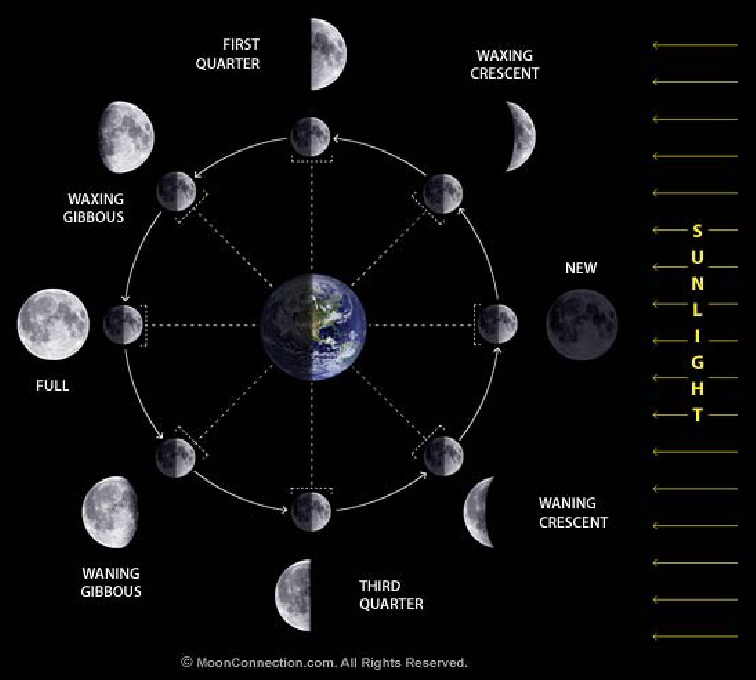
What causes the phases of the moon?

• Lunar phases are a consequence of the Moon’s 27.32-day orbit around Earth

• The Moon reflects light from the sun

• Half of the Moon is illuminated by the Sun, and half is dark

• We see a changing number of bright and dark faces as the Moon orbits

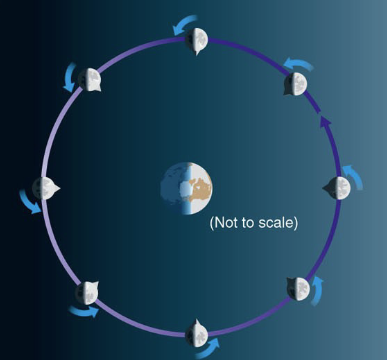
Why is there only one face of the moon visible from Earth?

Synchronous rotation: the Moon rotates exactly once with each orbit

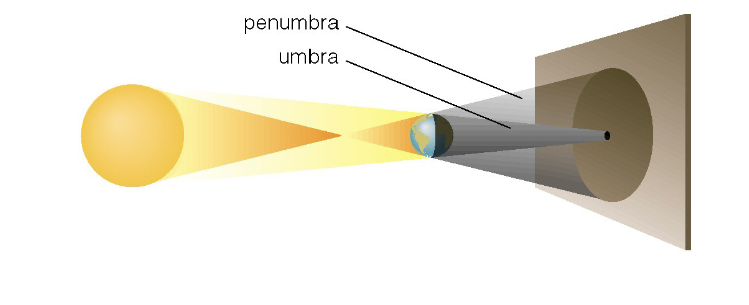
What causes eclipses?

• The Earth and Moon cast shadows. When either passes through the other’s shadow, we have an eclipse.

• The sun is 400 times larger than our moon and 390 times farther away

  • So, the sun and moon have nearly equal angular diameters. Thus, each is just the right size to cover the disk of the other