calc bc cylinders and quadric surfaces

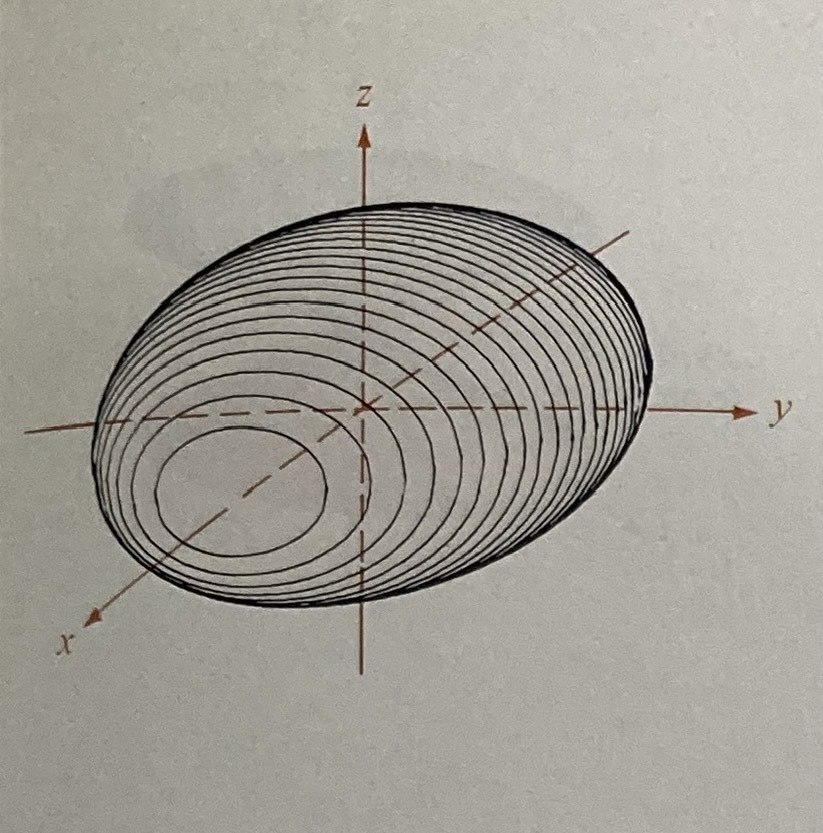
Ellipsoid

All squared, all positive, equals 1

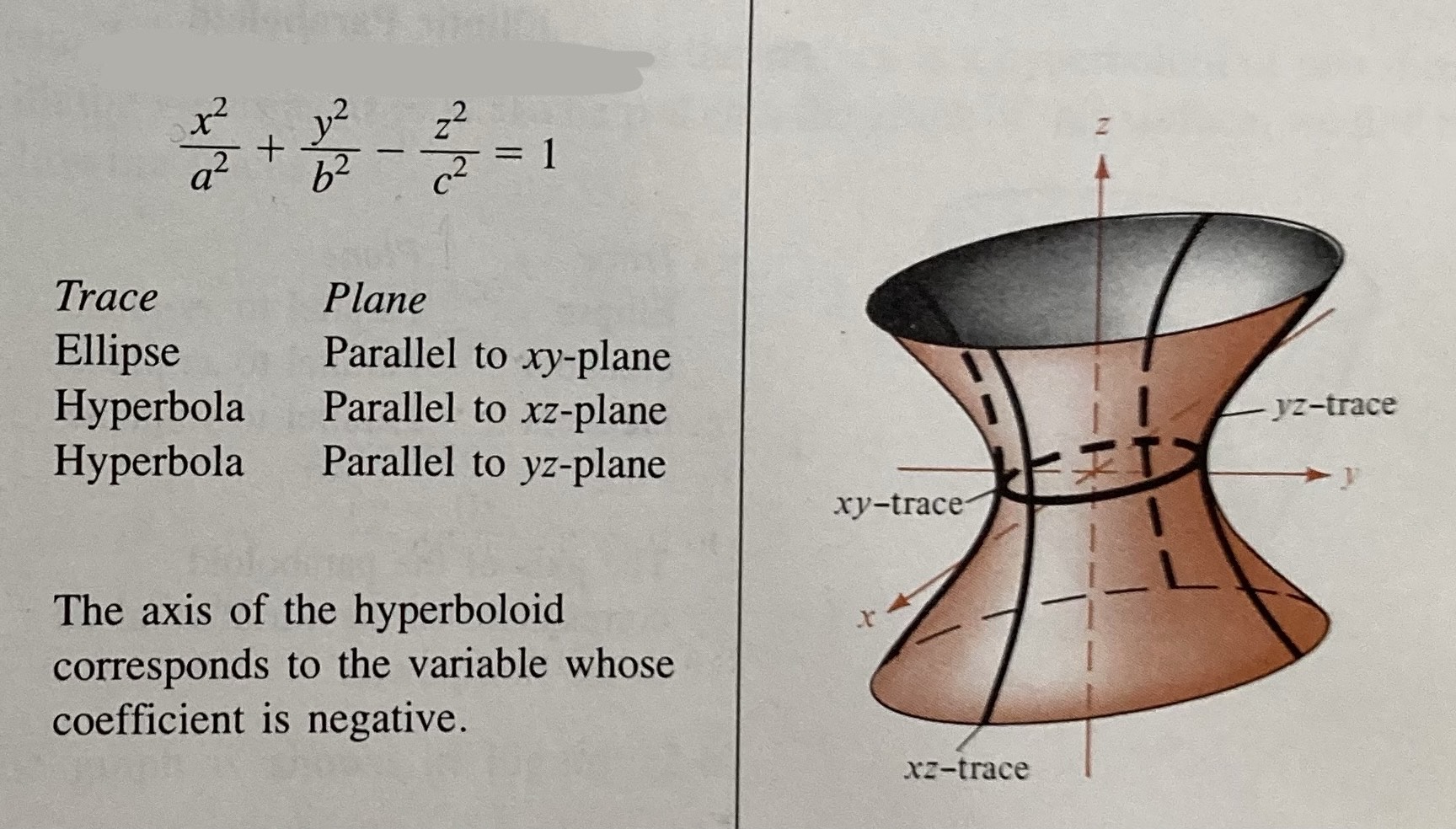
Hyperboloid of One Sheet

All squared, ONE negative, equals 1 (on negative’s axis)

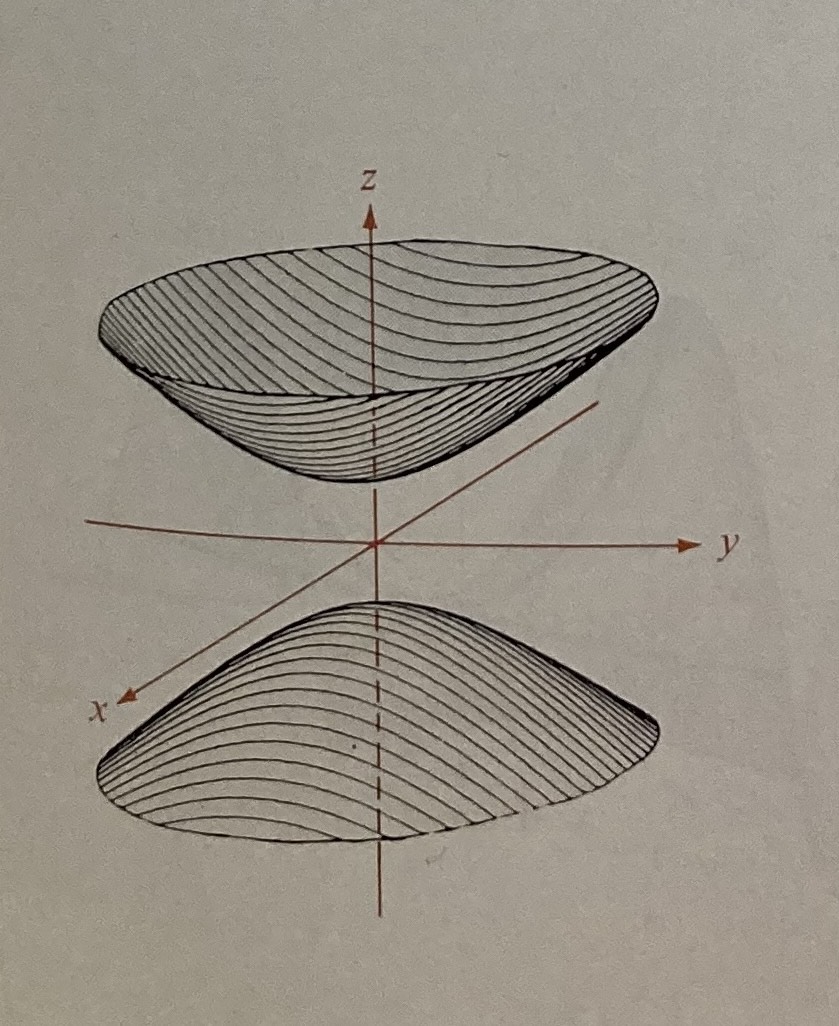
Hyperboloid of Two Sheets

All squared, TWO negatives, equals 1

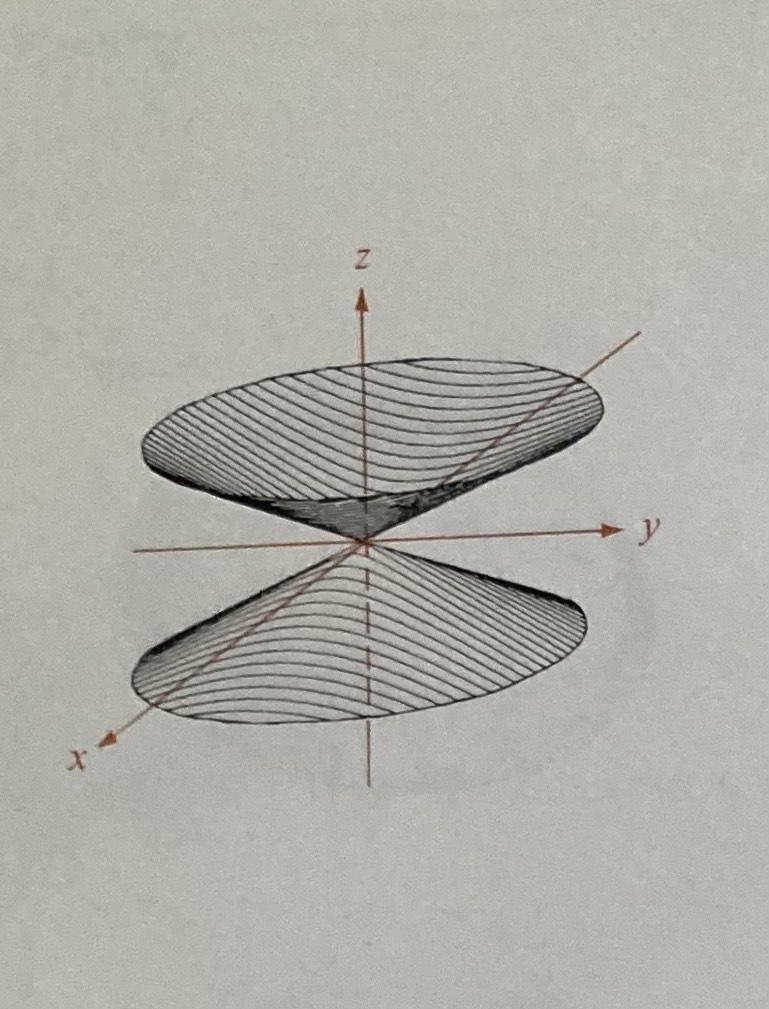
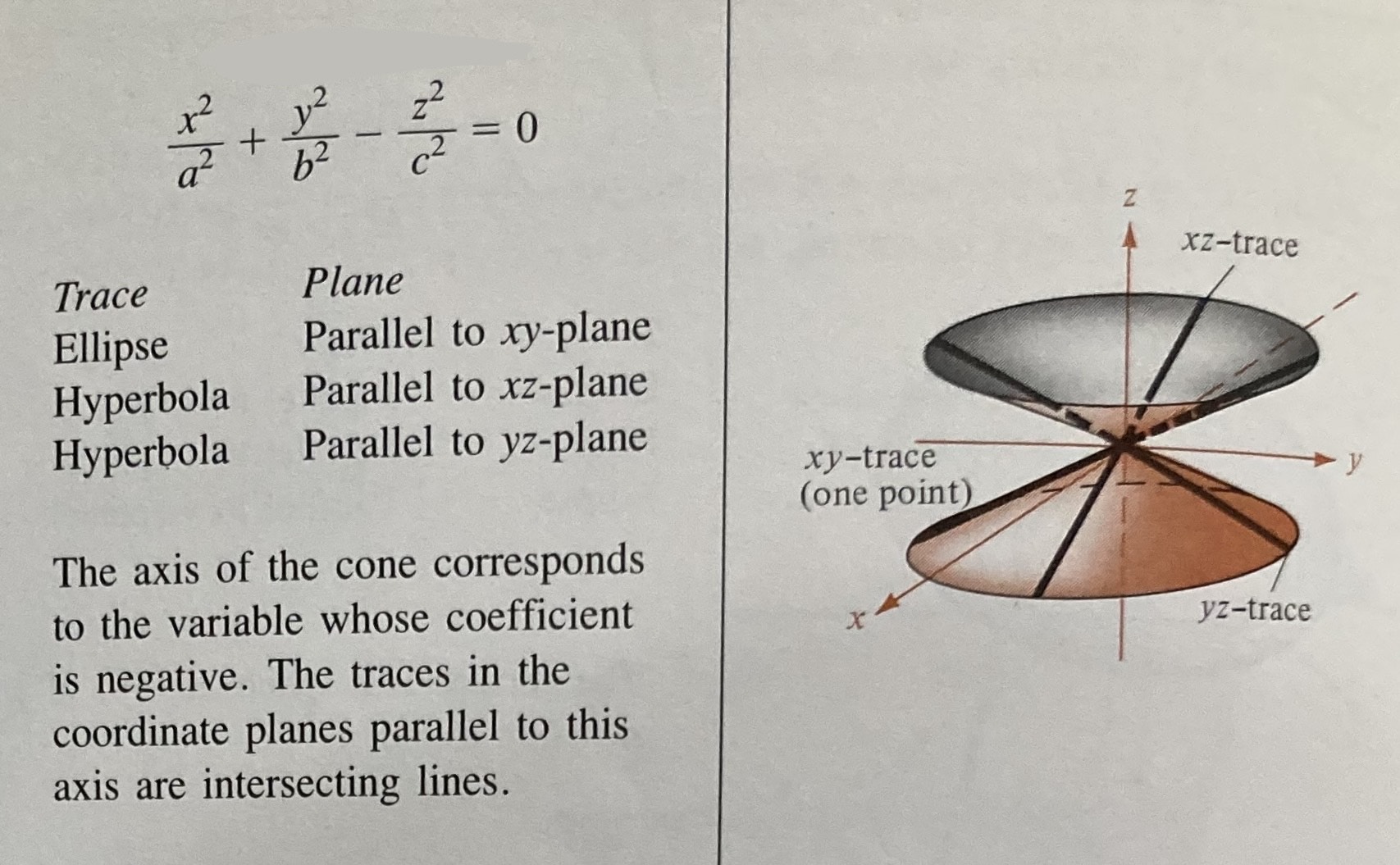
Elliptic Cone

All squared, ONE negative, equals zero

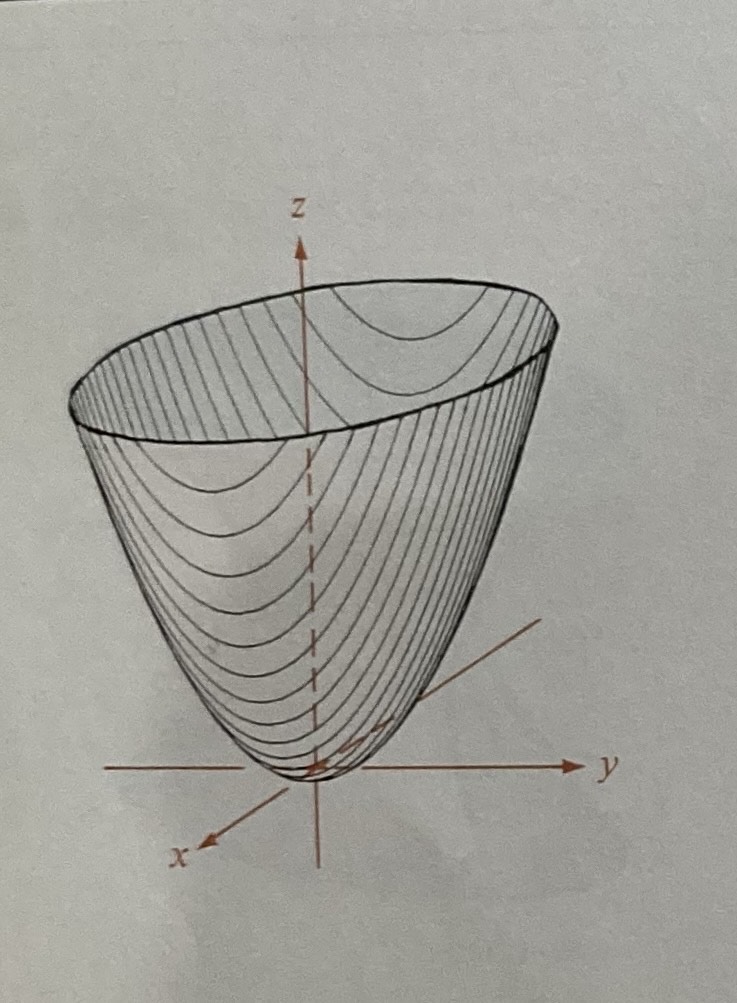
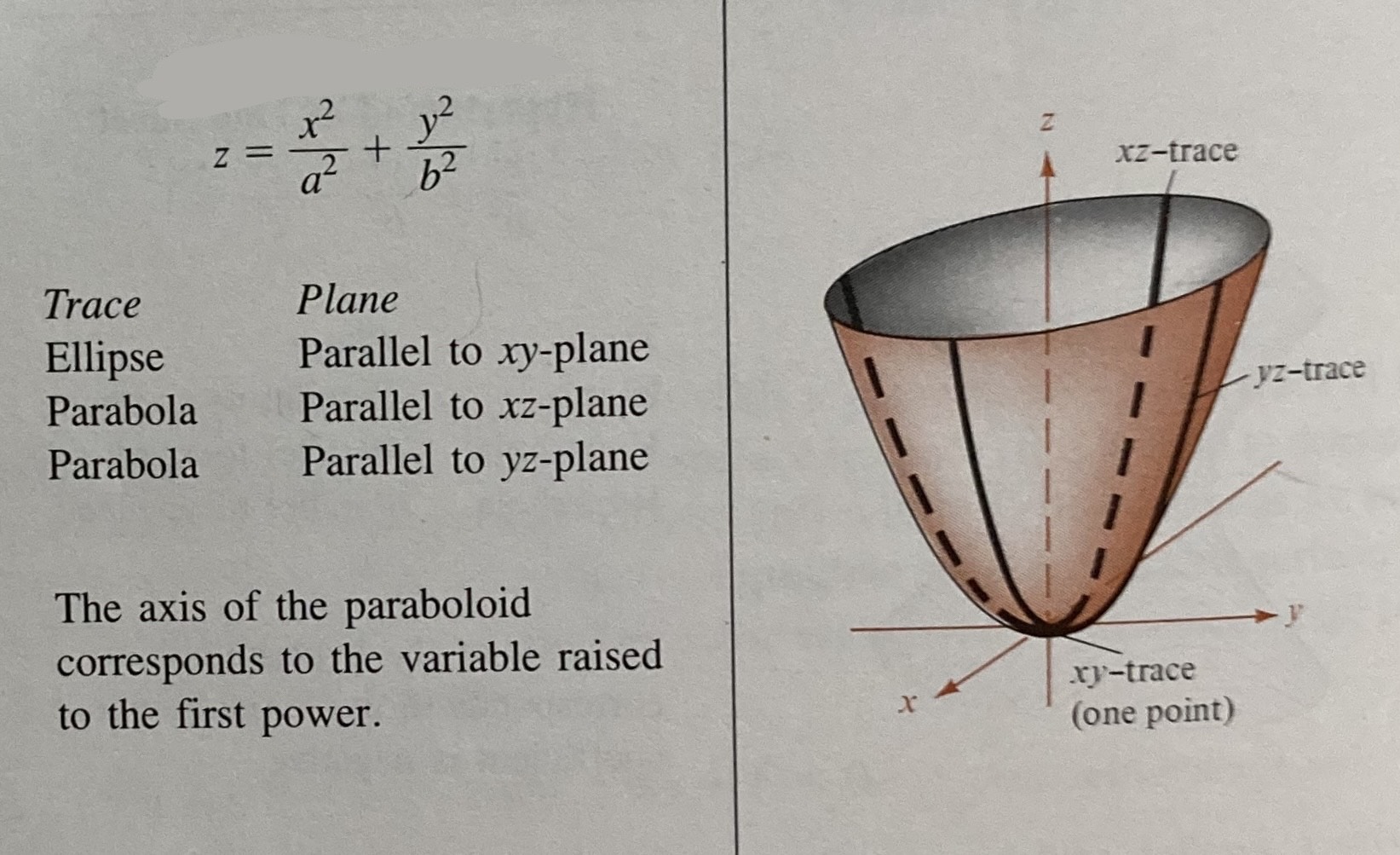
Elliptic Paraboloid

TWO squared, all positive, equals non-squared variable

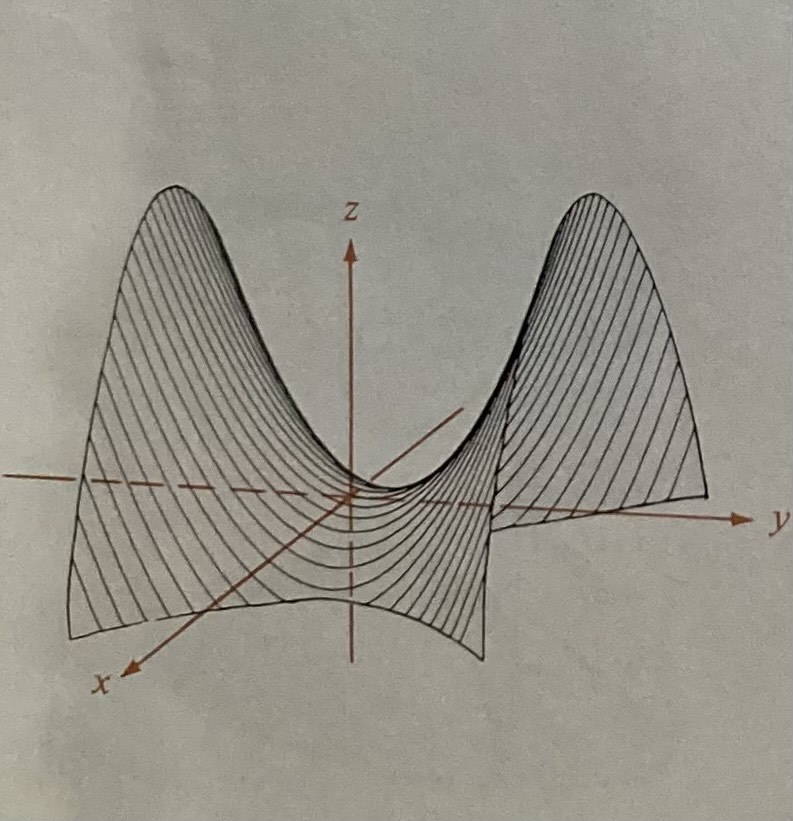
Hyperbolic Paraboloid

TWO squared, ONE squared negative, equal to non-squared variable

Rectangular/Cartesian coordinates

(x, y, z)

Cylindrical coordinates

(r, θ, z)

r = radius/distance from origin (xy axis, 2D)

θ = angle

z = height

Spherical coordinates

( p, θ, Φ)

p = distance from origin (3D)

θ = angle

Φ = angle from z-axis

find x (cylindrical to rectangular)

r cosθ

find y (cylindrical to rectangular)

r sinθ

find z (cylindrical or rectangular)

z

find r (rectangular to cylindrical)

sqrt(x² + y²)

find θ (rectangular to cylindrical)

tan^-1 (y/x)

find x (spherical to rectangular)

p sinΦ cosTHETA

find y (spherical to rectangular)

p sinΦ sinTHETA

find z (spherical to rectangular)

p cos Φ

find p (rectangular to spherical)

sqrt (x² + y² + z²)

find Φ (rectangular to spherical)

cos^-1 (z/ sqrt(x² + y² + z²) )

find p (cylindrical to spherical)

r / sinTHETA

find r (spherical to cylindrical)

p sinΦ

find r (spherical to cylindrical)

p sinΦ

find z (spherical to cylindrical)

p cosΦ

what shape?

p = n

sphere

what shape?

THETA = pi/n

plane orthogonal to xy plane going through origin

what shape?

Φ = pi/n

elliptic cone (half)

what shape?

Φ = +— pi/n

elliptic cone (full)

what shape?

r = n

right circular cylinder (toilet paper roll)

what shape?

z = n

plane parallel to xy plane, up n units