Research Psychology Exam 2 (PSY:2811)

relative frequency table

shows the percents of observations in each category or class

calculate relative frequency

proportion= frequency of bin/ total of all frequencies

for relative frequency, what do you want to proportion numbers to add up to?

1 or 100

proportion can also be expressed as...

a percentage

cumulative frequency tables

count accumulated scores across bins

calculate cumulative frequency

frequency of row + cumulative frequency of above bin

absolute frequency

the number of times a score or value occurs in a data set

percent of total

bin count/ total count

what is shown on the x-axis of a histogram

possible values

what is shown on the y-axis of a histogram

frequency (proportion or percentage)

bins should be...

1. equal sized
2. exclusive without gaps
3. exhaustive of all possible scores

increment of values on the y-axis should be...

equal sized

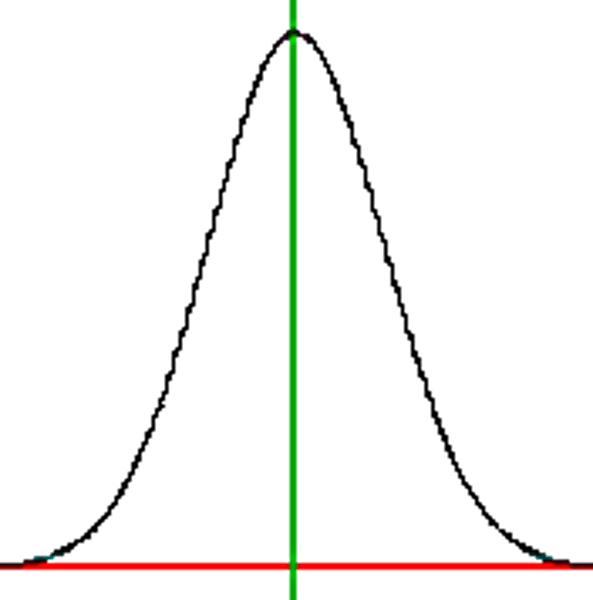
normal distribution

symmetrical distribution of data with a single peal and a bell shape

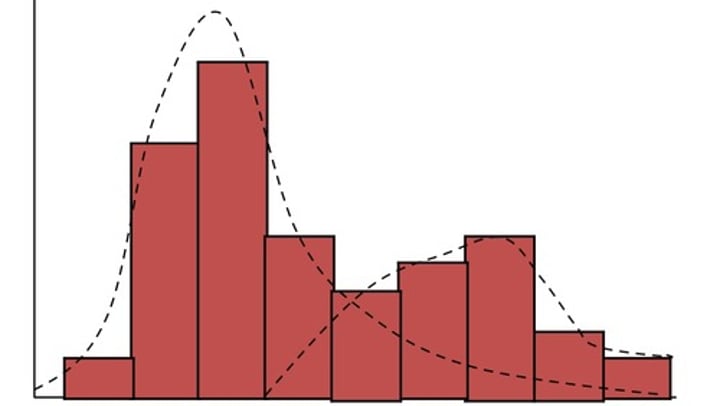
bi-modal distribution

distribution with two peaks

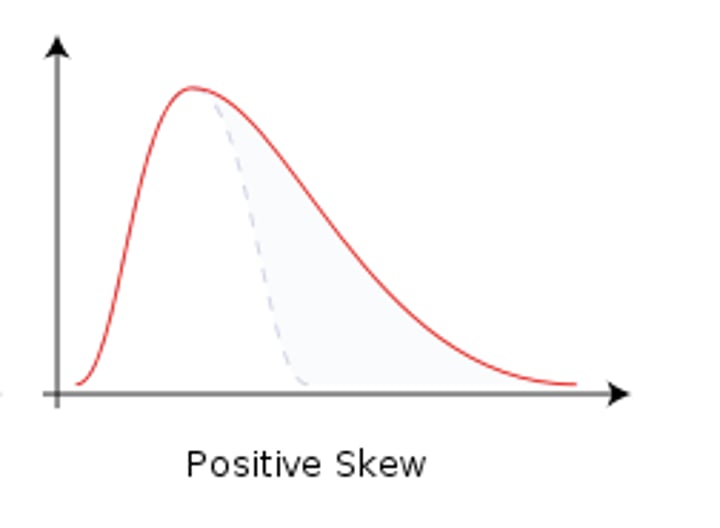
skewed distribution

distribution has off-centered peaks

negative skew (left) order

(left to right)
1. mean
2. median
3. mode

positive skew (right) ordr

(left to right)
1. mode
2. median
3. mean

measures of central tendency

mean, median, mode

mode

most frequently occurring score

the only and best measure for nominal variables

mode

nominal variable

no order, ex. eye color

ordinal variable

you can order them, but you can't put a number on it (agree/ disagree)

multiple peaks often means...

there are sub-groupings within the sample, consider separating for further analysis (think Kentucky derby example)

median

the middle value in a frequency distribution

when is median best used

when the shape of the distribution for interval/ ratio variable is skewed

mean

average

calculate mean

sum of all scores (X)/ number of scores (n)

when is mean best used

when the shape of the distribution for interval/ ratio variable is symmetrical (not skewed) and unimodal

nominal (symmetric, skewed and multi-modal)

mode

ordinal, symmetric

median

ordinal, skewed

median

ordinal, multi-modal

mode(s)

interval, symmetric

mean

interval, skewed

median

interval, multi-modal

mode(s)

ratio, symmetric

mean

ratio, skewed

median

ratio, multi-modal

mode(s)

central tendency

a measure that represents the typical response or the behavior of a group as a whole

variability between multiple people

students will score differently from each other

variability within a given participant

some score within a person may fluctuate as time goes on

random measurement error

score is higher, or lower than the "true" score, doesn't affect average, only the variability around the average

systematic measurement error

measure of a construct is consistently offset from the "true" score, does affect the average (called bias), central tendency will be shifted

range

a measure of variability that indicates how wide the distribution is

calculate range

highest value - lowest value

range is highly susceptible to...

outliers

IQR

tells us how spread out the most commonly occurring values are in the distribution

what do the whiskers represent in a box and whisker plot

range

what do the boxes represent in a box and whisker plot

IQR

normal distribution box and whisker plot

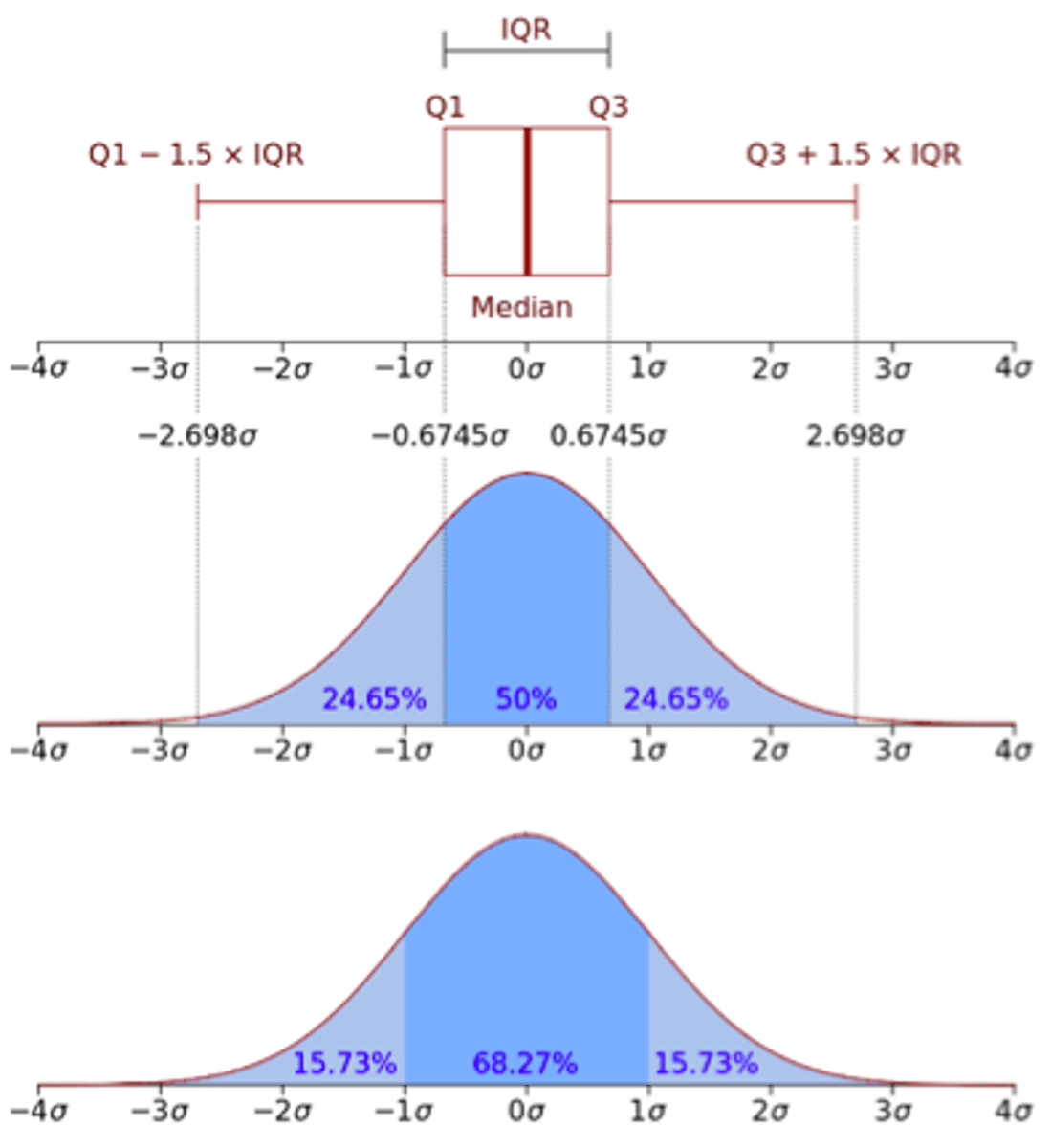
multi-modal with short tails box and whisker plot

positive skew box and whisker plot

deviations

how much each date point deviates from the mean

greater deviations mean

greater spread, greater variability

negative deviation

score is less than the mean

positive deviation

score greater than mean

calculate deviation

score - mean
xi - X

the total negative deviation will always be the same as...

the total positive deviation

absolute deviation

absolute value of all deviation scores

mean absolute deviation

mean of the absolute deviation
total/ # of scores

distributions with higher M.A.D. have...

a greater spread of scores

which kind of plots help visualize central tendency, shape of distrib., and variability

histogram, box and whisker plot

sum of squares

the sum of the squared deviation scores

calculate sum of squares

sum of individual scores - (sum of individual scores^2/ number of scores)

difference between population ad sample estimates for the sum of squares

different symbols

population sum of squares

μ and N

sample sum of squares

x̄ and n

variance

estimate of average sum of squares

calculate variance

σ^2= SS/N

calculate sample space (variance for a sample)

s^2=SS/n-1

degrees of freedom

number of scores that can vary in the calculation of a statistic

degrees of freedom has a bigger effect on...

smaller samples

calculate standard deviation

√(SS/N)

calculate sample standard deviation

√(SS/n-1)

when do you use sample standard deviation

when you measure from a sample to infer about a larger population

when do you use population standard deviation

highly unlikely

what is a z-score

number of standard deviations away from the mean

z-scores are helpful for...

comparing across measures with different units of measurement

calculate z-score

(score-mean)/ standard deviation

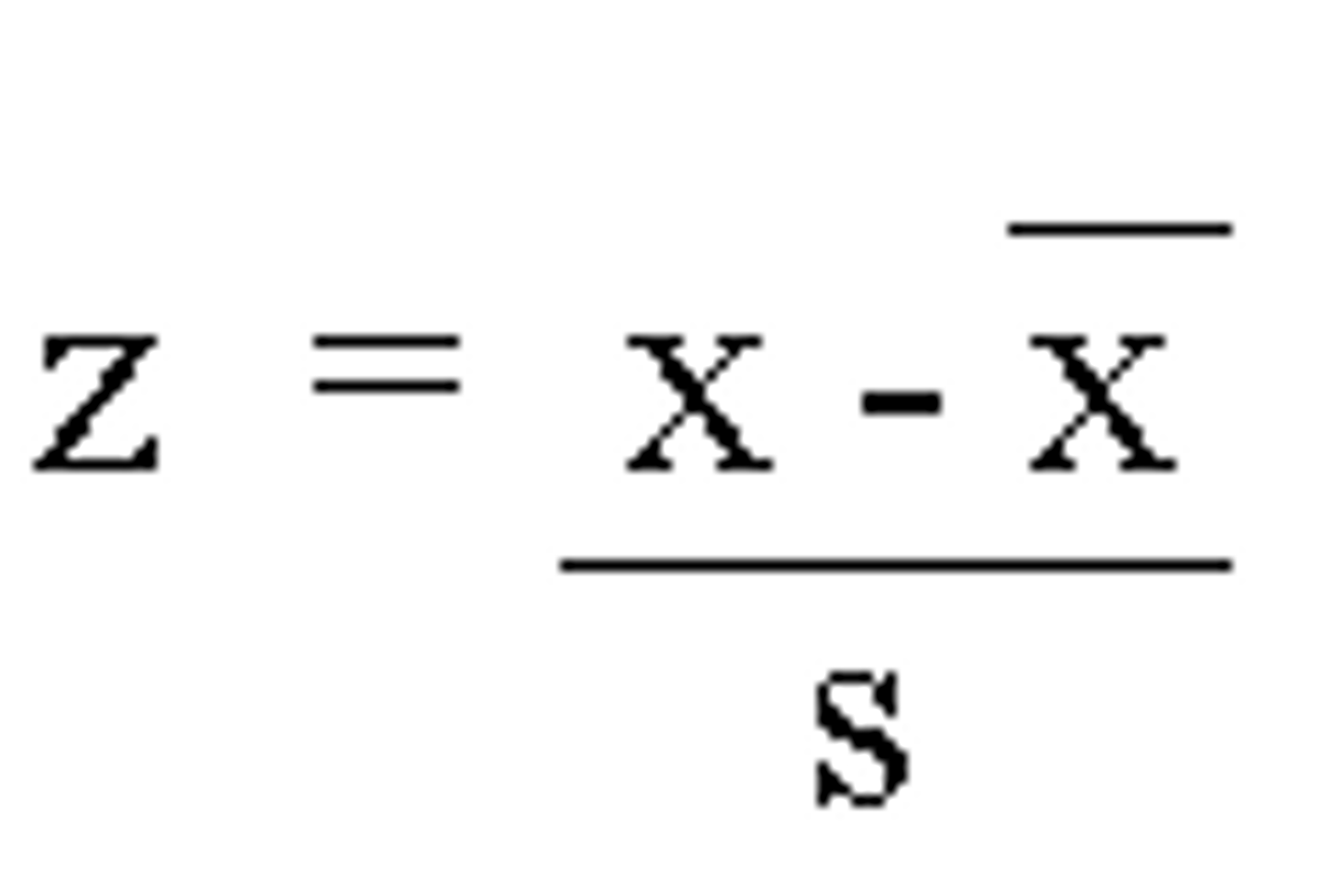
standard curve

easy acess to information about proportion under the curve

z-score of 0 means...

he data point's score is identical to the mean score

how can z-scores identify outliers

all scores less than or greater than 3 SDs from the mean is considered an outlier

what kind of claim do you use the Pearson r

correlational claim (association)

when to use pearson correlation

to quantify the direction and strength of the relationship between 2 quantitative variables of at least interval measurement scale

correlation statistic

describes the direction and strength of the relationship between 2 quantitative variables

quantitative variables

factors that can be counted

how can correlation strength be found

how close the points are to a trend line, the close to 1/-1 the better

how can correlation direction be found

the slope, pos./neg.

calculate r

sum of cross products/ √(SS for x)(SS for y)

calculate cross product

(score of x - mean) * (score of y - mean)
add all of them up

what indicates strength and direction in the statistic (pearsons r)

the numerator

what indicates strength and direction in the scatter plot (pearsons r)

negative correlation: x value higher than mean, y value lower than mean
positive correlation: x value lower than the mean, y value higher than the mean

if an extreme score (outlier) in the same direction is taken out, how does this affect the correlation

it gets weaker

if an extreme score (outlier) in the middle is taken out, how does this affect the correlation

it gets stronger

if an extreme score (outlier) in the opposite direction is taken out, how does this affect the correlation

it gets stronger/ stays the same

range restriction

occurs when the range of scores obtained for a variable has been artificially limited in some way

when you reduce variability (range restriction)...

the correlation will decrease