Goemtrey Unit 12- Transformations

Pre Image versus image

Pre image = The points before the transformation

Image = points after a transformation, notated with ‘

Translate

To slide (ridged motion), preserves angle measure and segment length

—> notated as (x,y)—> (x+ / - #, y + / - #)

Reflection

To flip, must include what you are reflecting over (aka: line of reflection)

—> line of reflection is the perpendicular bisector of the segment formed between the pre image and image

Dilate

NON rigid motion

To make something bigger/smaller proportionaly, to move points closer or further from the enter of dilation

—> must include center point and scale factor

—> dilated point = closer to further from another point, dilated line = longer or shorter

—> if dilated by n the area is n² and the perimeter is n

—> Dilated line = only change the y intercept by the scale factor

—> pRESERVE: Angle measure, shape, orientation

—> do NOT PRESERVE: Distance, congruence

—> if you can map on by dilation they are similar

Define “map onto”

If you can map a shape onto another shape using dilation they are ____

If you can map a shape onto another shape using transformations they are ____

Map onto: al points in a figure can be placed on top of a point on another figure

—> rigid motions (translation,rotation,reflection): shapes are CONGRUENT

—> non-rigid motions (dilations): shapes are SIMILAR

Rotational symmetry

If it can be rotated and mapped onto itself (ignore 0 and 360)

—> if regular polygon = can be mapped onto itself using any multiple of the measure of each angle, ex: regular decagon 360/10 =36, anything multiple of 36 will carry it onto itself

Point symmetry

If it has 180 rotational symmetry

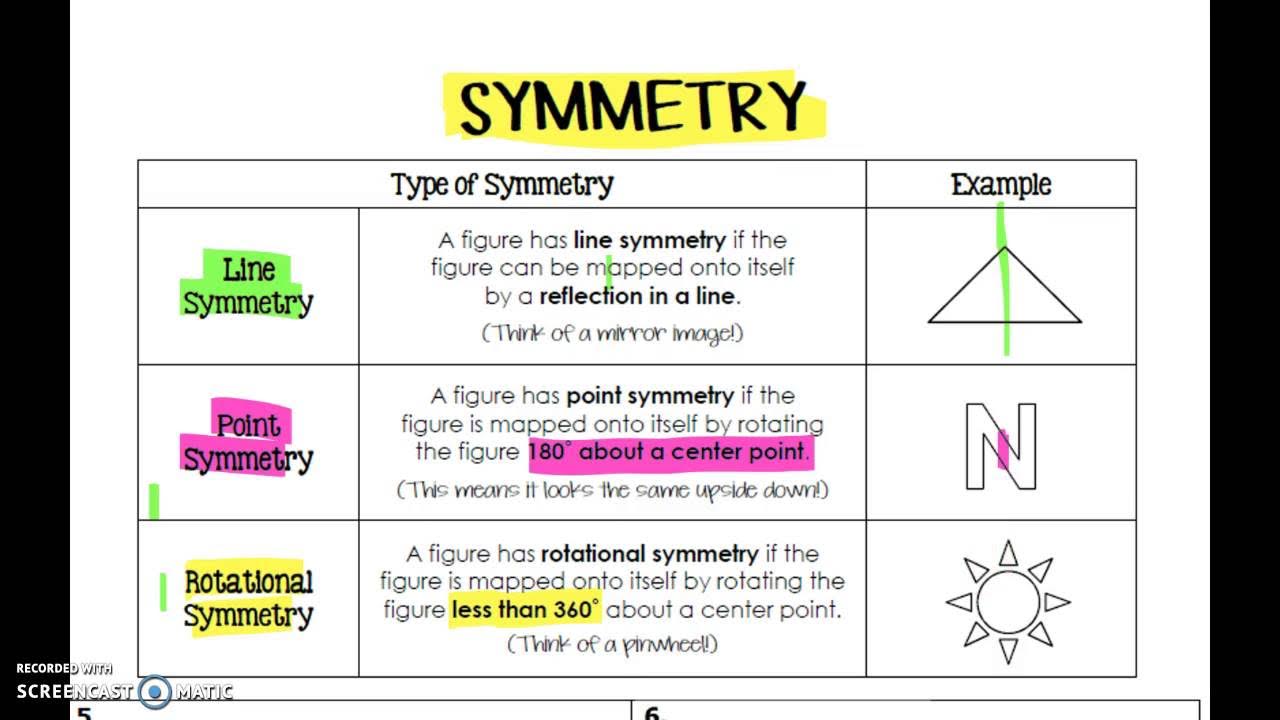
Line symmetry

If a shape can be reflected and mapped onto itself

Vector

Direction and magnitude (length)

—> same vector means they have the same direction and magnitude, doesn’t matter where they are placed

Tesselation

Geometric pattern that completely cover the plane (flat surface) without any gaps or overlaps

Ex: hexagons, triangles

Name all “-agons” 1-12

Line of reflection

What the points are being reflected over, also the perpendicular bisector of the segment formed by the two points (image and pre image)

—> count away from reflection line (equidistant)

—> labele points

Label your points!!!

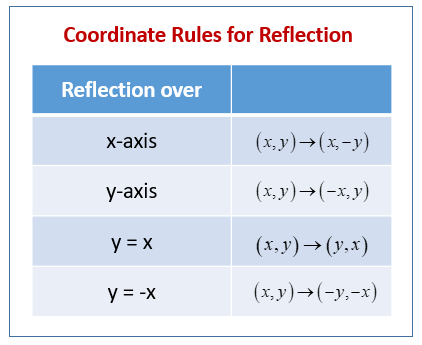
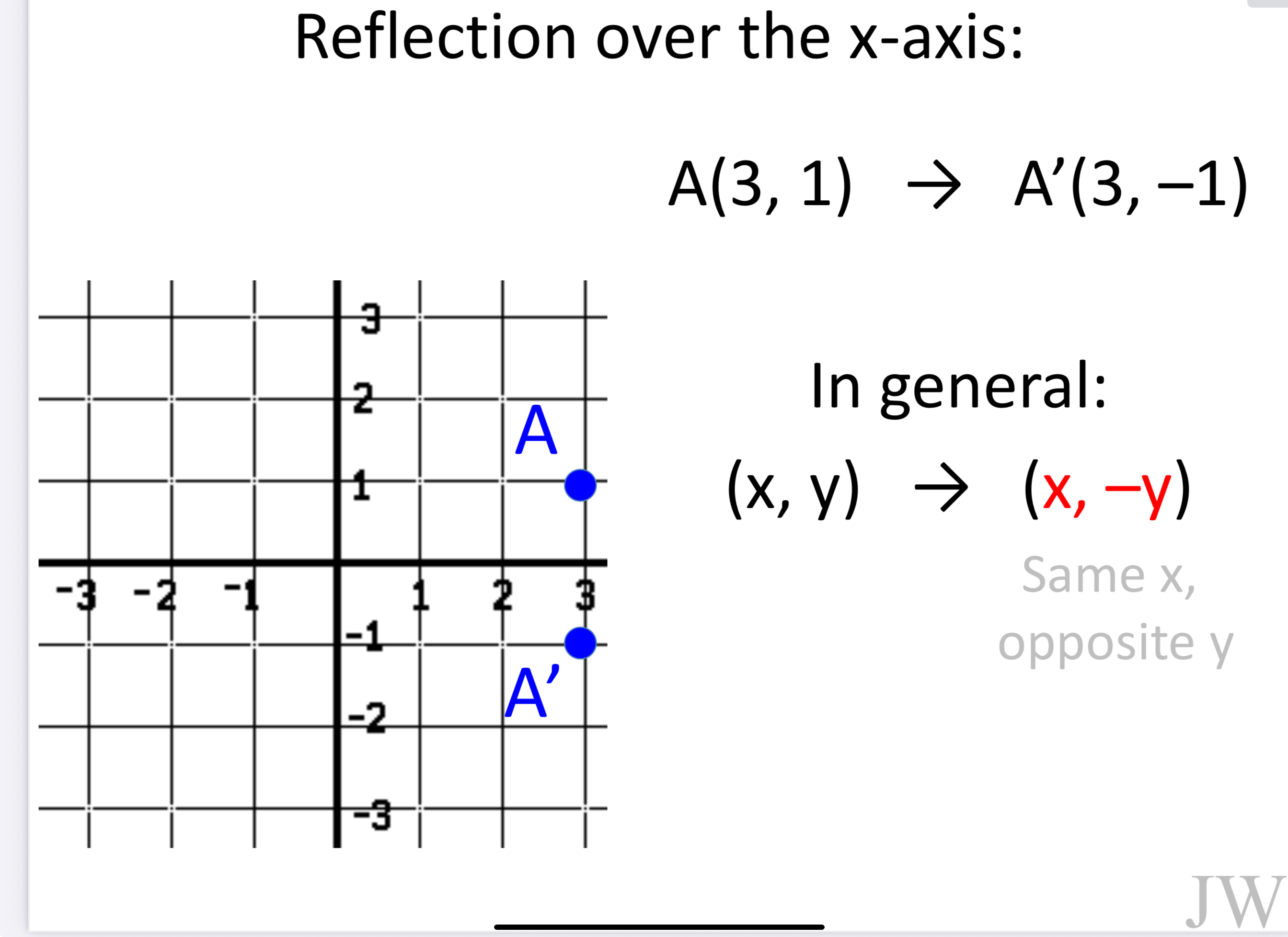
Reflected across…

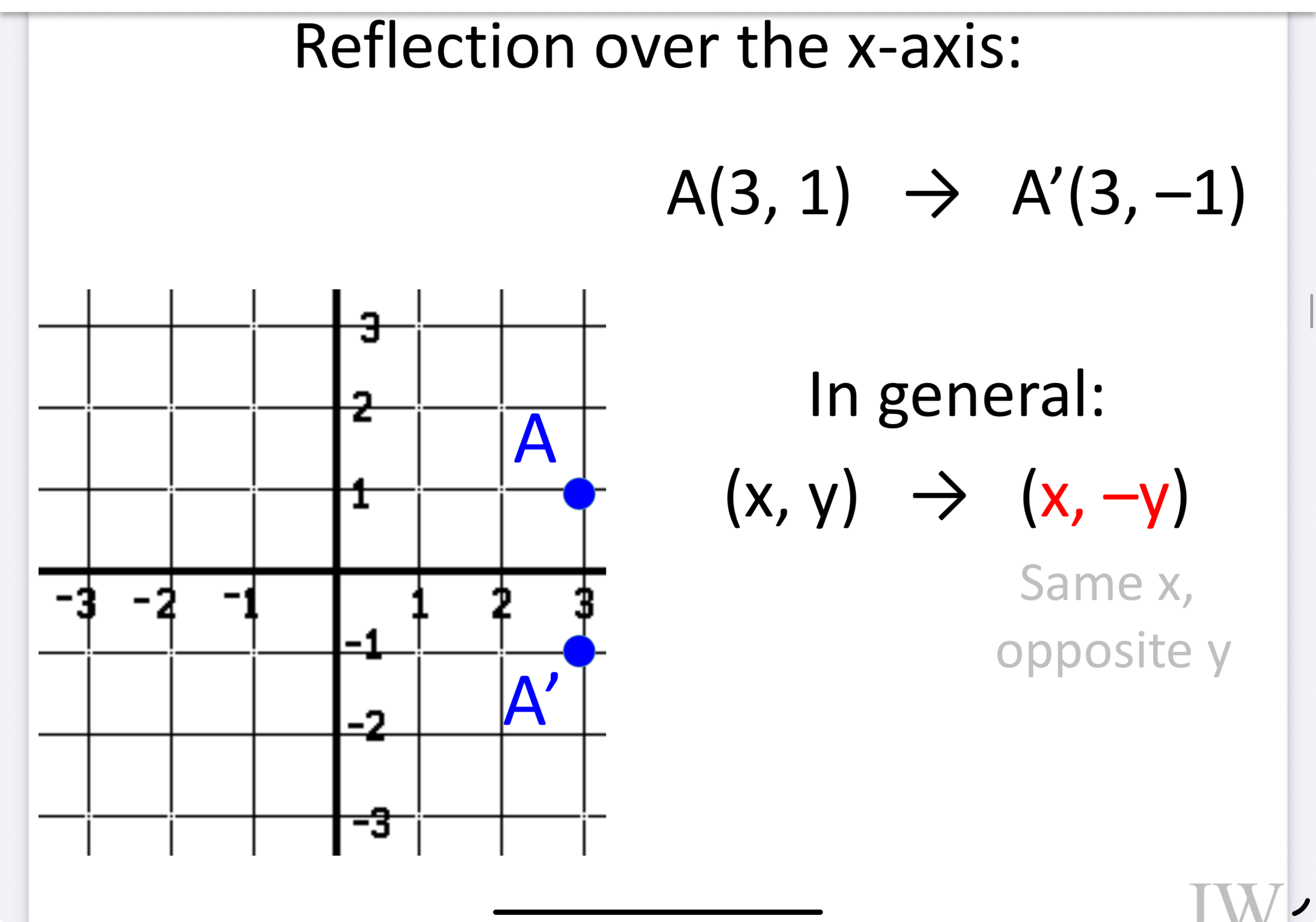
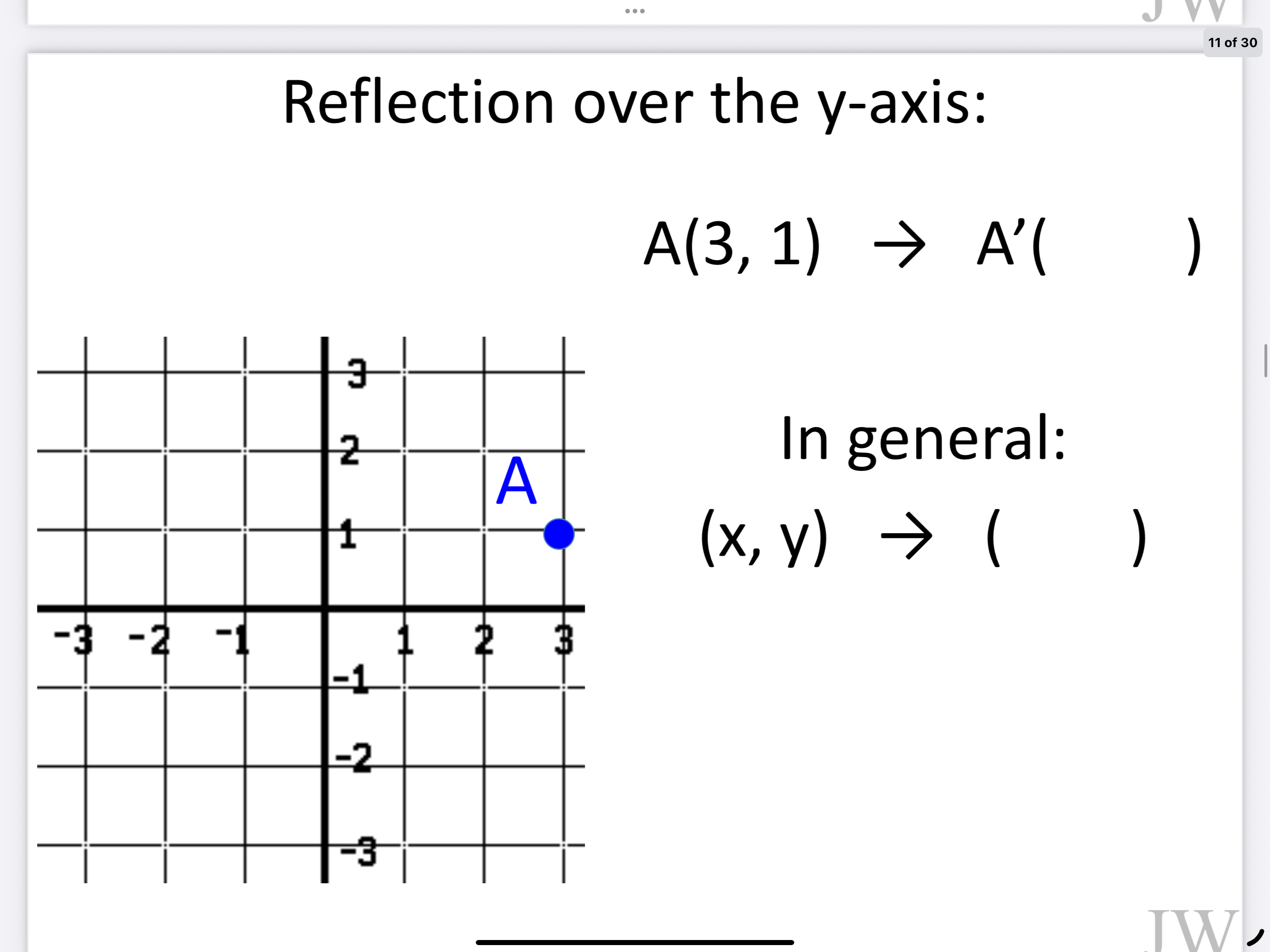
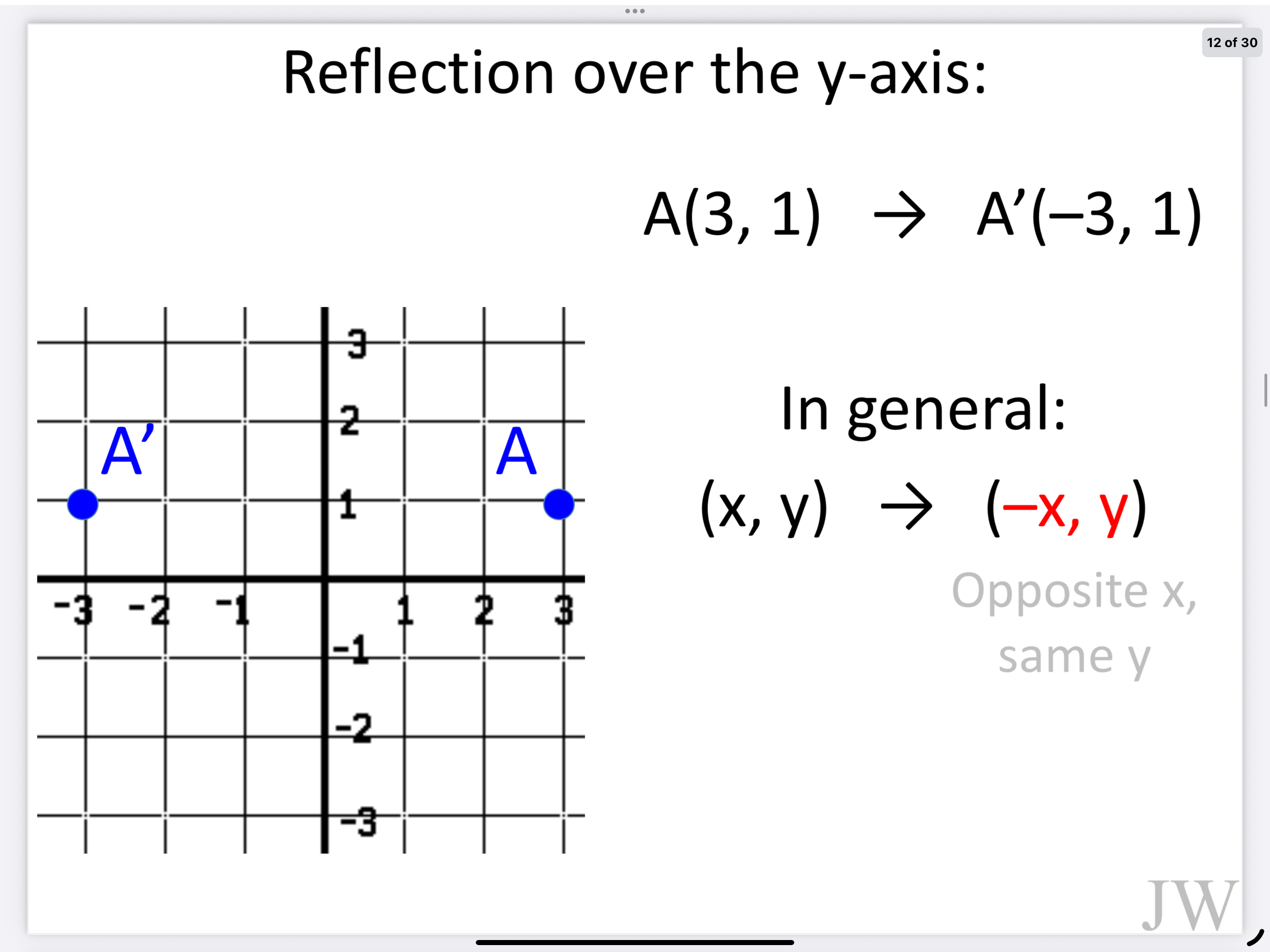
Y - axis

X - axis

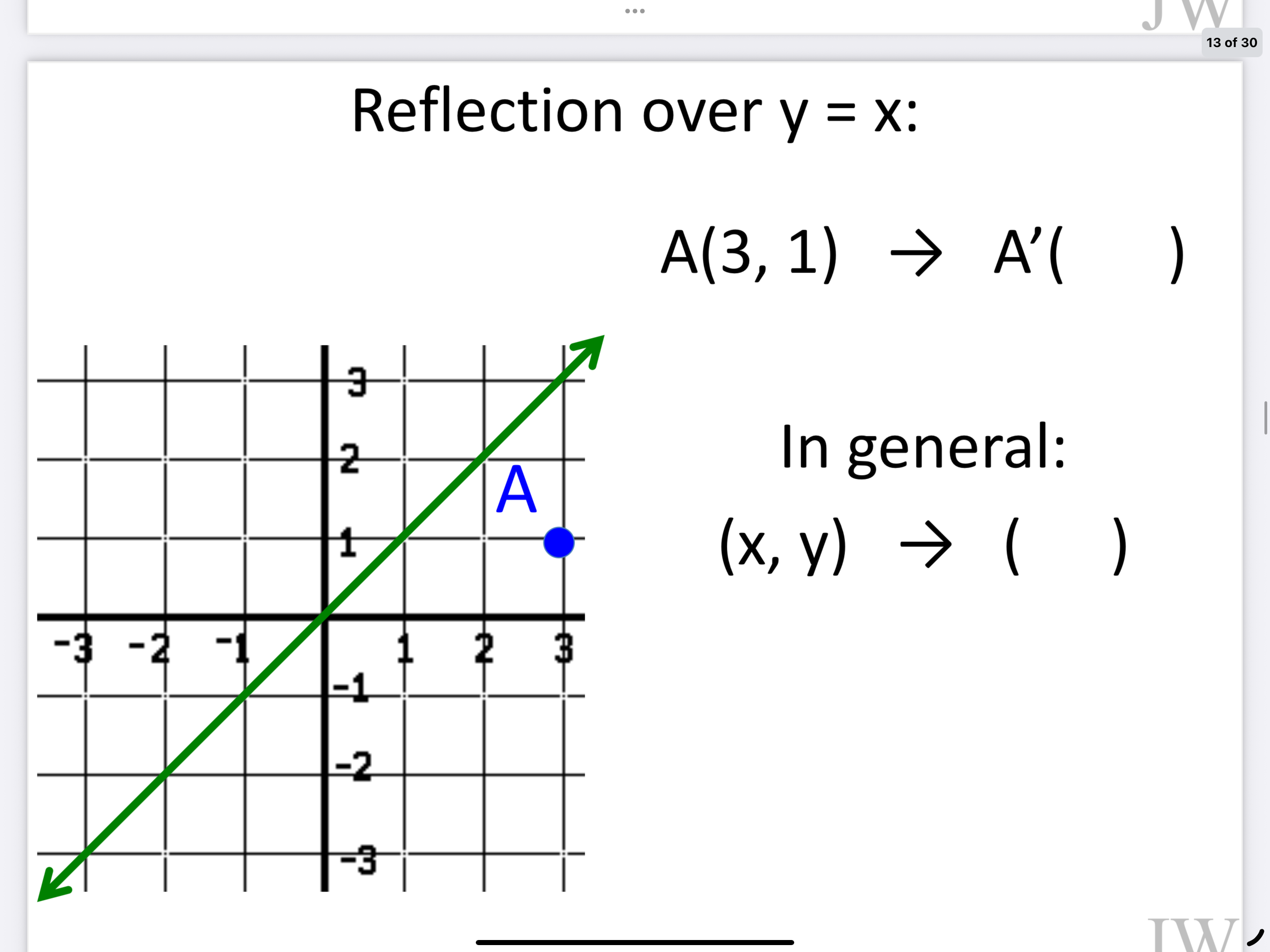
Y = X

Y = -X

Y -axis = (x, y) —> (-x, y)

X - axis = (x, y) —> (x, -y)

Y = x (x,y) —> (y,x)

Y= -x (x, y ) —> (-y, -x)

How to dilate an image

1) find length and mark it with a arc

2) replicate length by scale factor using compass (arc)

3) label new point with apostrophe

—> before: draw a line between center of dilator and the point you are dilating

Why: dilation of a point = moving a point closer or further

How to dilate a line (equation)

1) multiple the y - intercept by scale factor using

2) slope stays the same, only the y-intercept changes

3) ***MUST CHECK if the center is on the line (plug in the solutions in equation) then the equation does NOT change

Preserve

To stay the same

Rigid motions: preserve distance and angle

Dilations: preserve slope and angle

Rigid motion

Translations, rotations, and reflections.

—>Transfformations that produce a new figure congruent to the original figure

—> figures before and after the transformation are congruent

—> dilations are not rigid

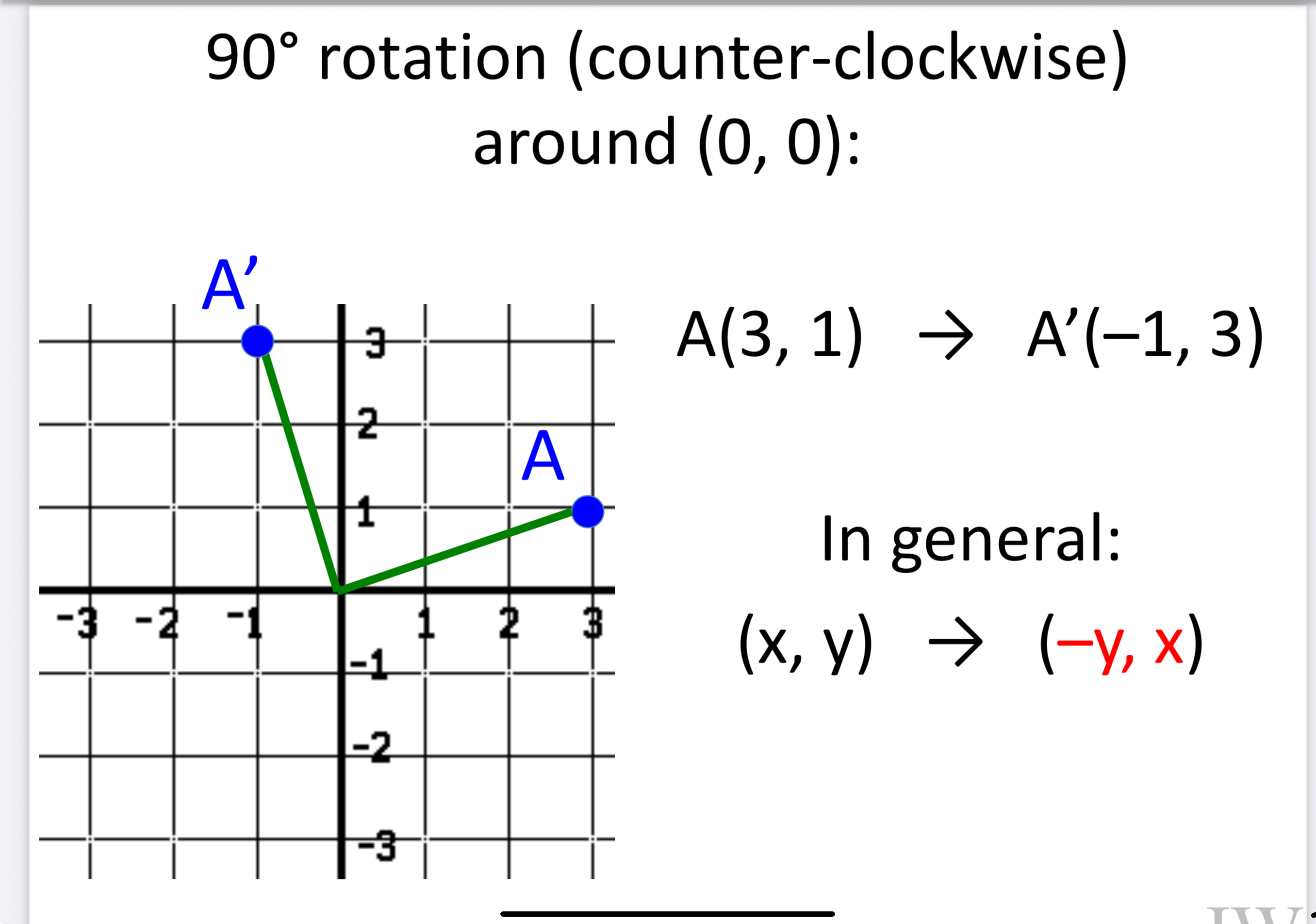
What is the rule for any counter clockwise 90 degree rotation

What is the rule for any 180 degree rotation

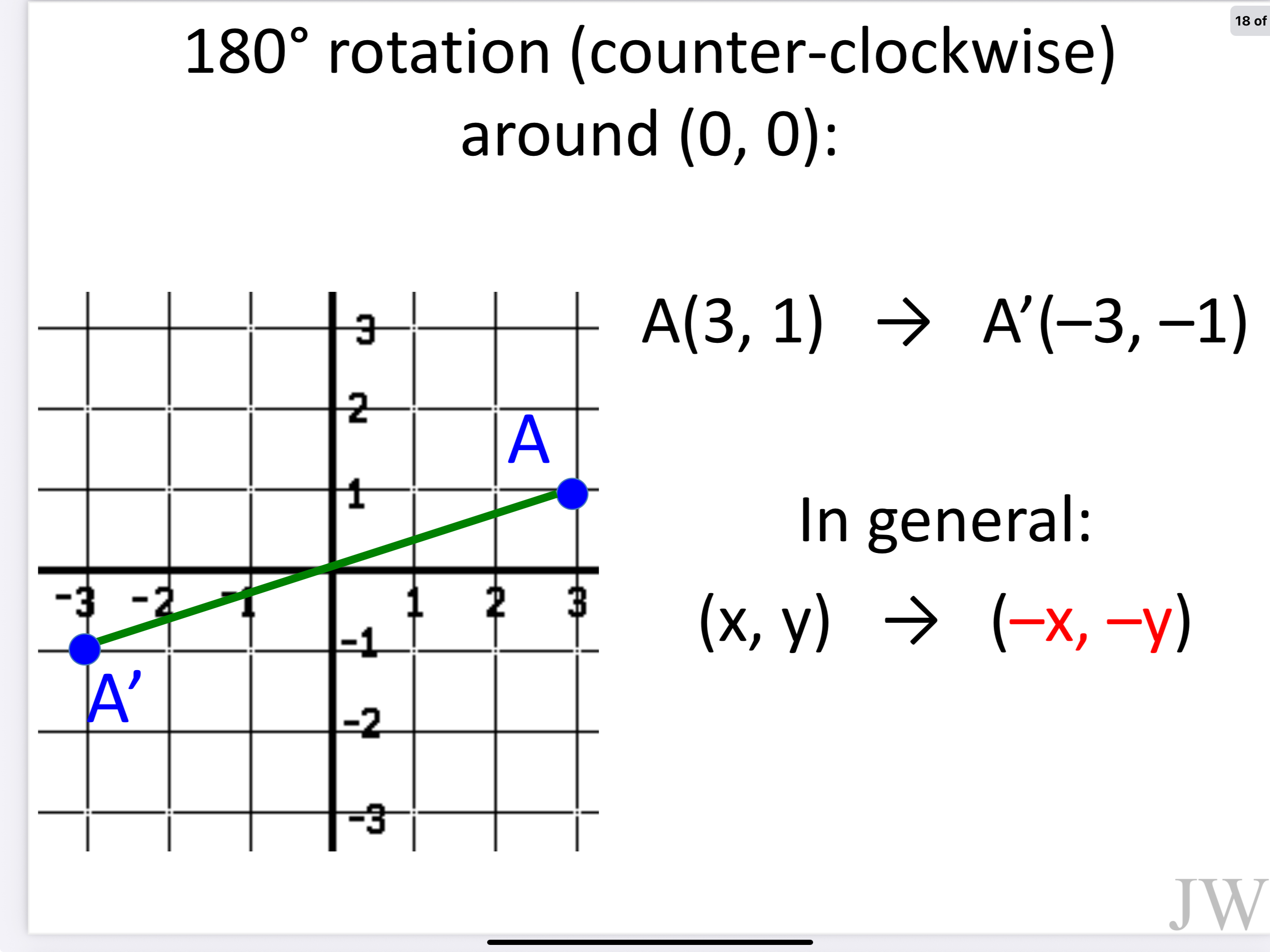
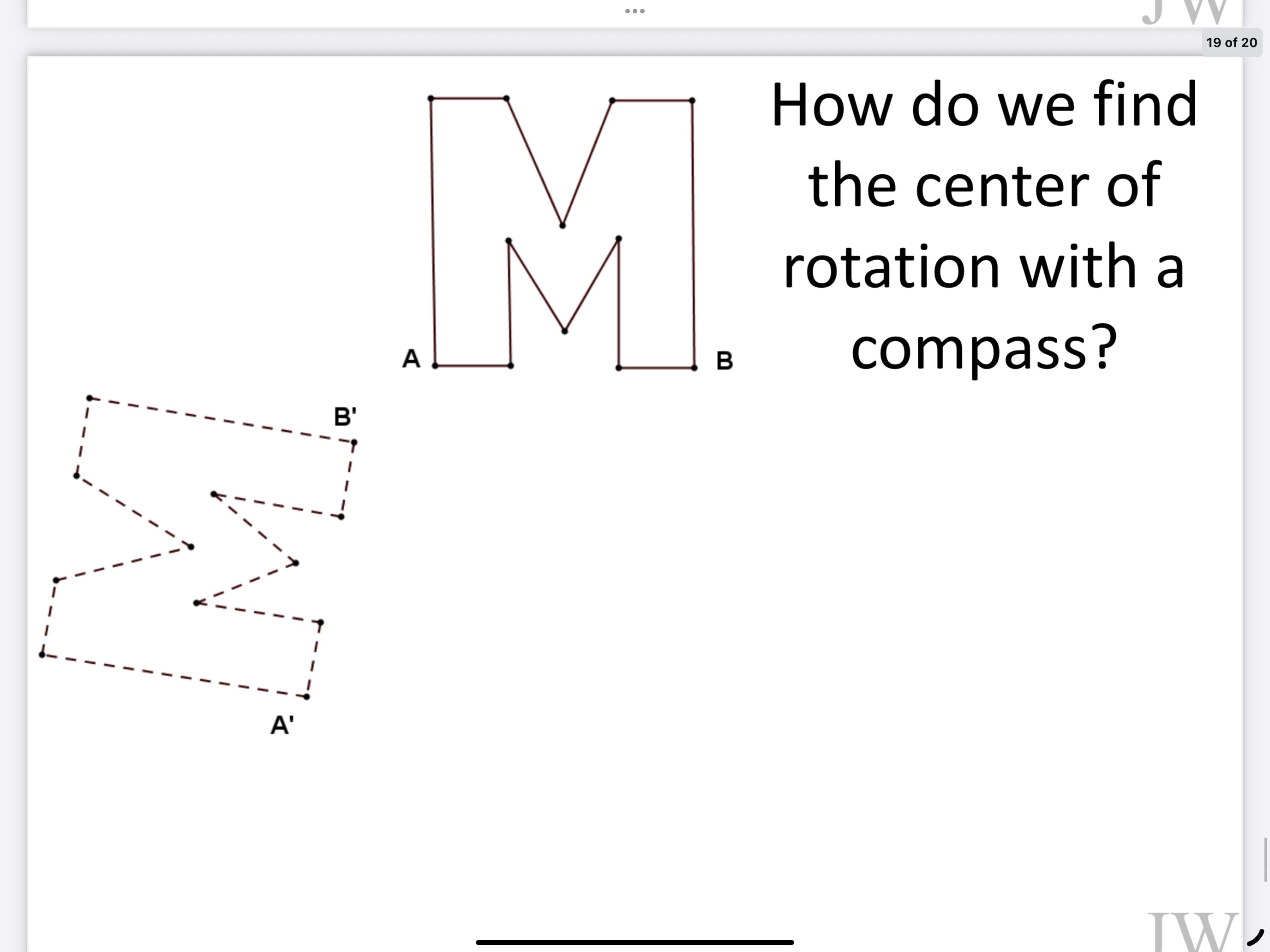
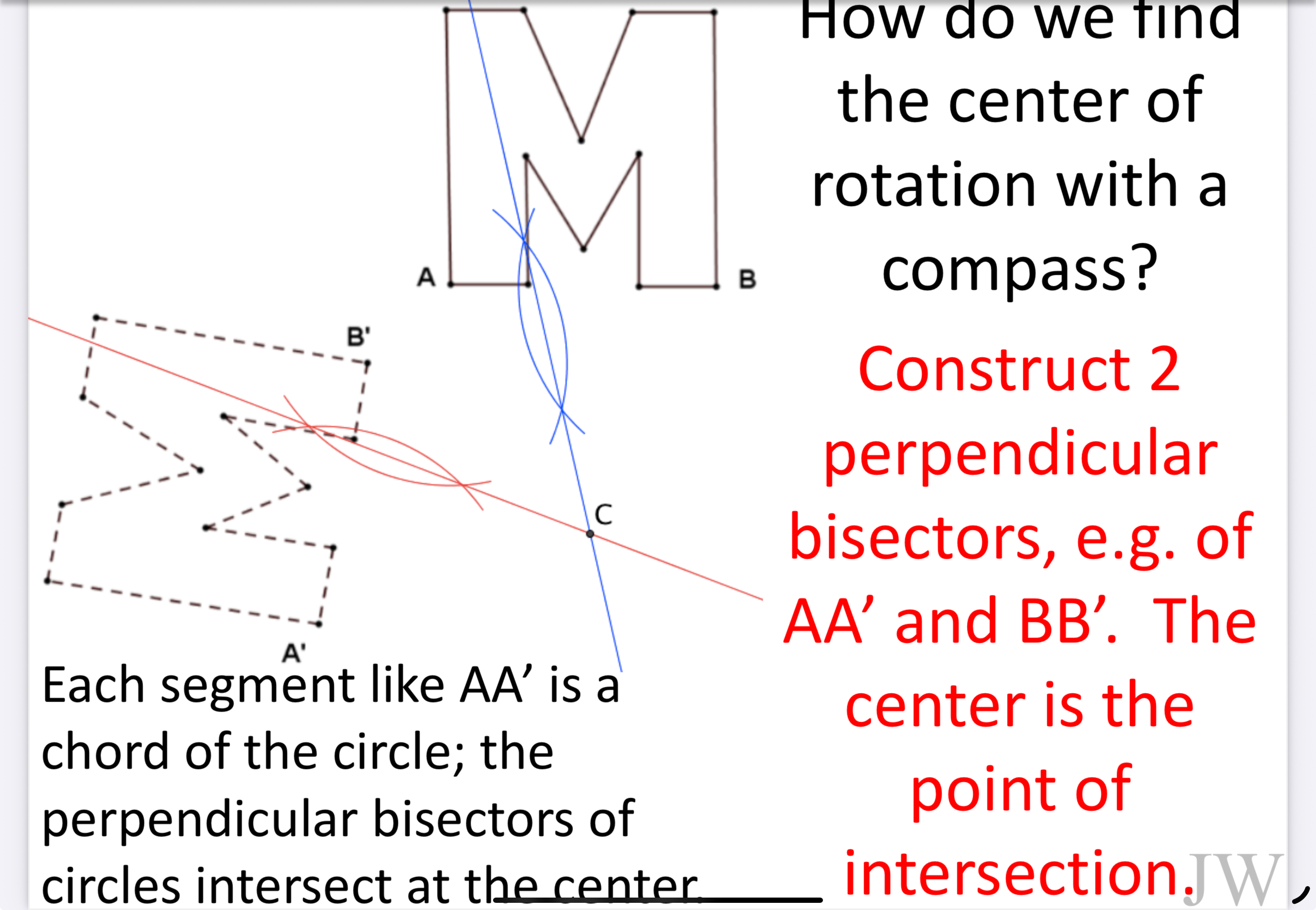
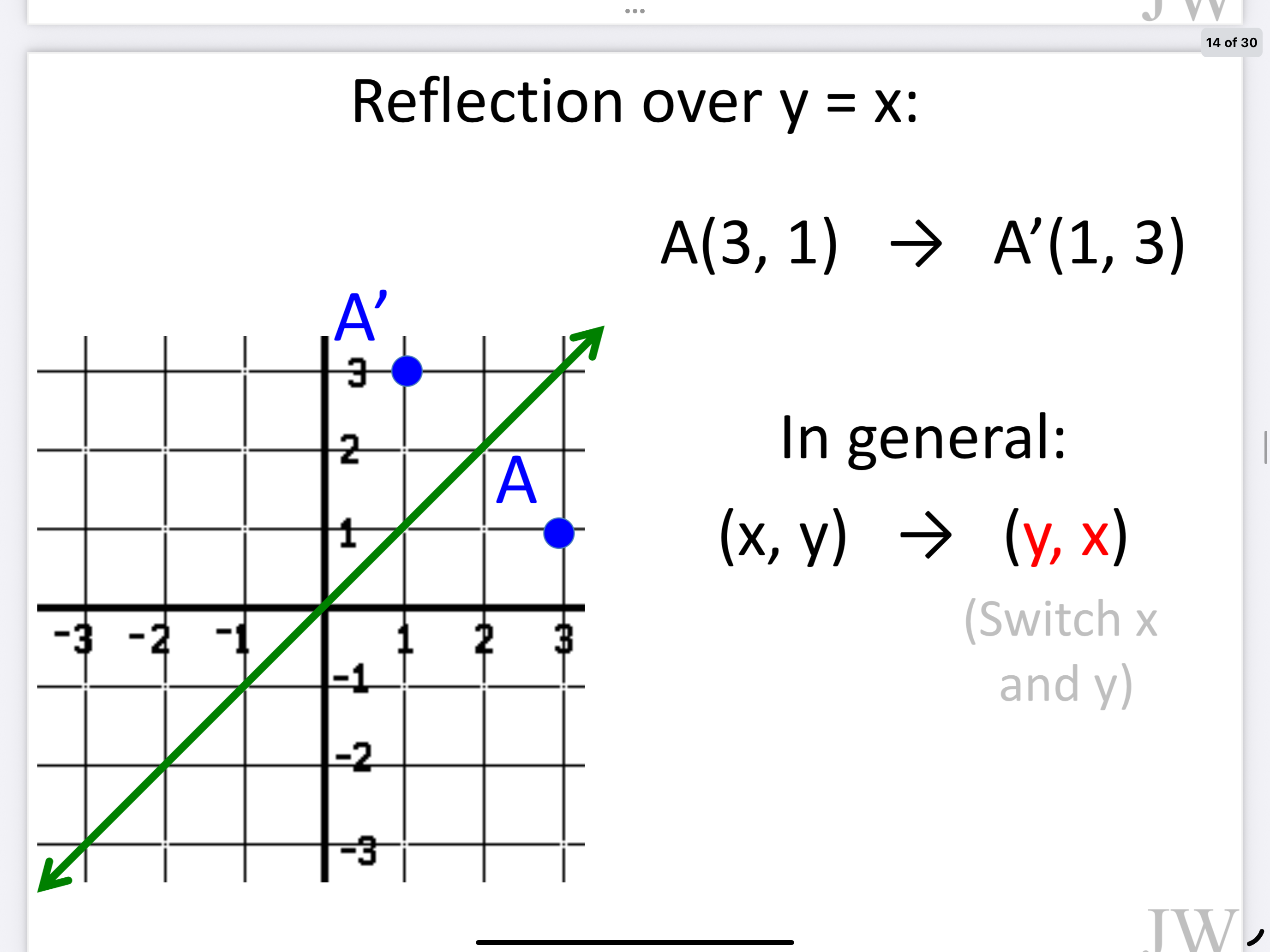
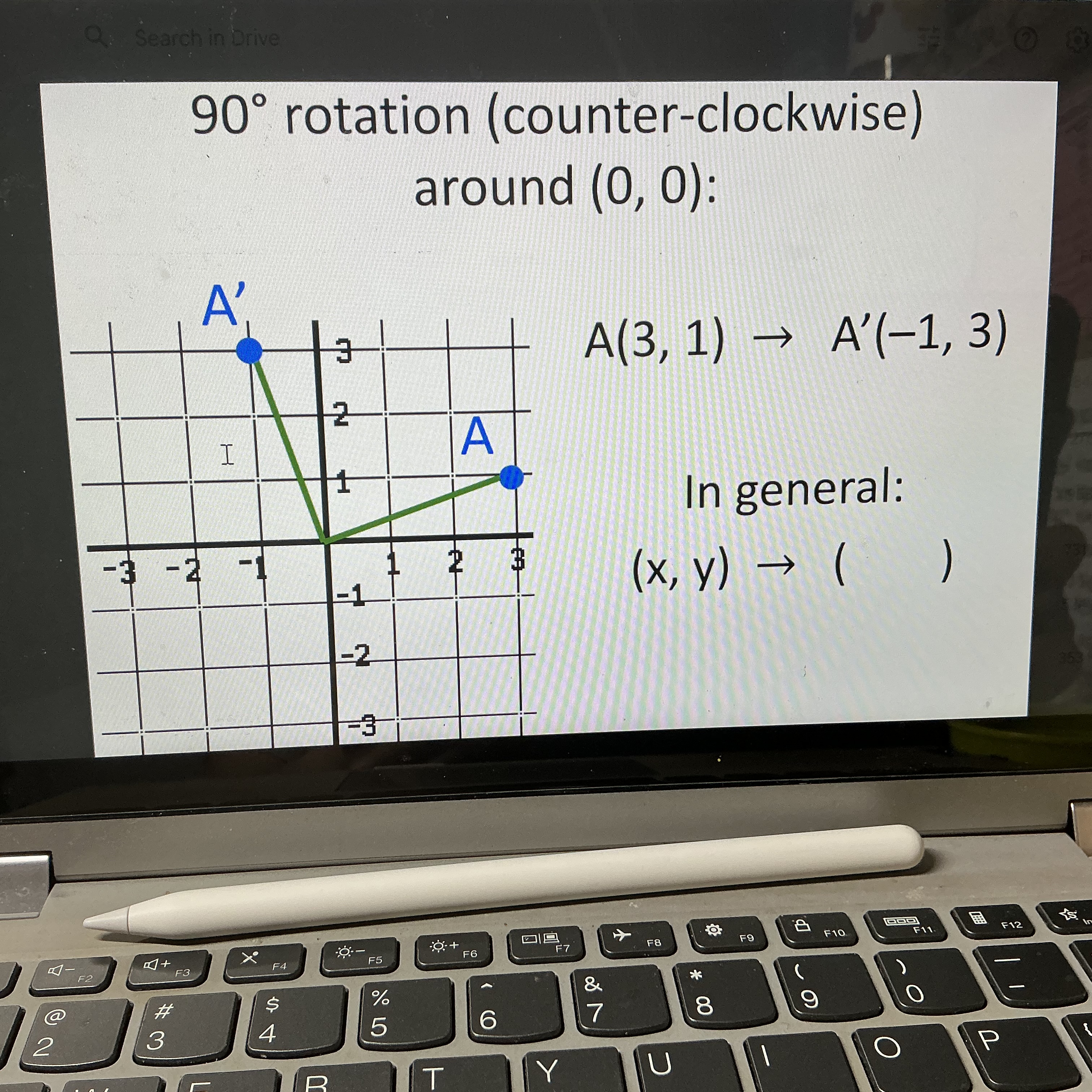
The slope of the line connecting the point being rotated and the other point (image and pre image) should be perpendicular (forming right angle) meaning they should have negative reciprocals (you can count from the center of rotation!)

IN GENERAL: (x,y) —> (-y,x)