Dynamics Midterm #1

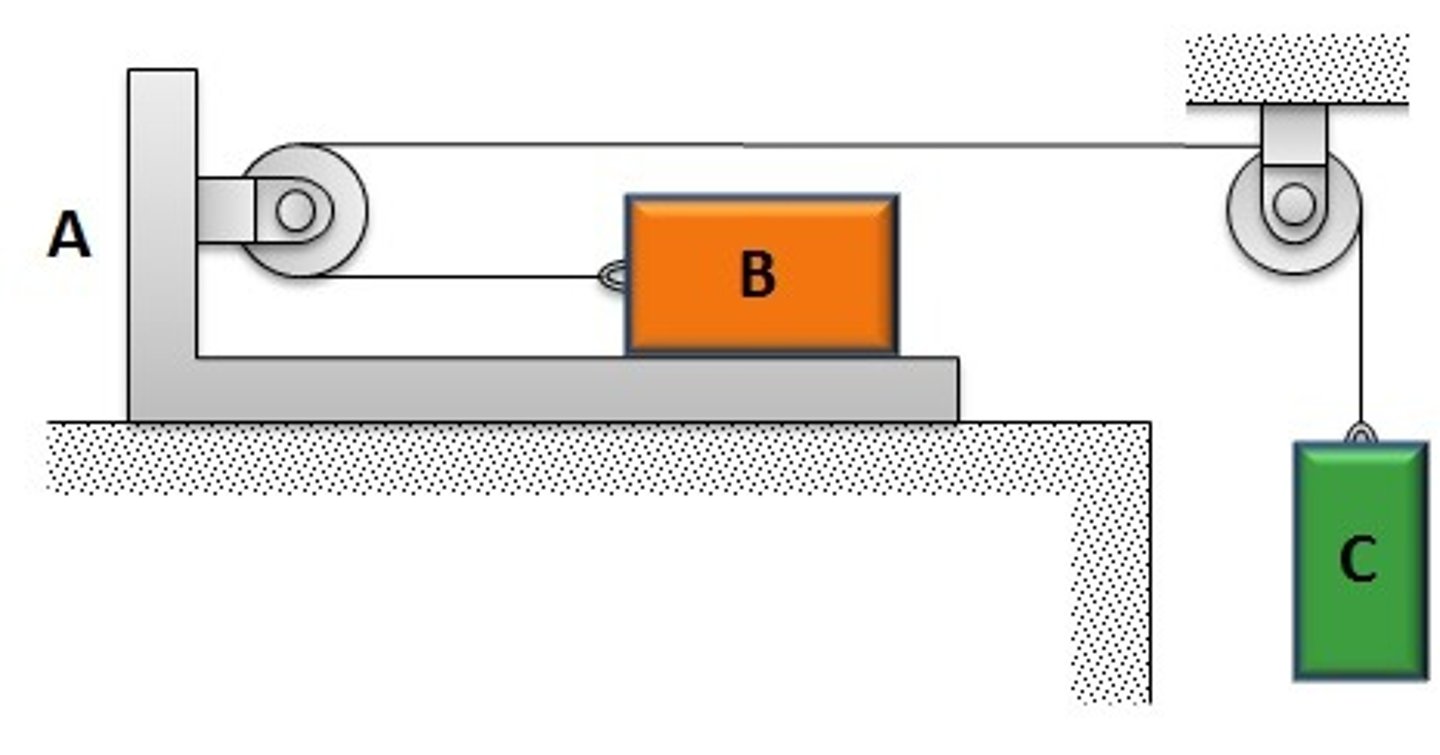
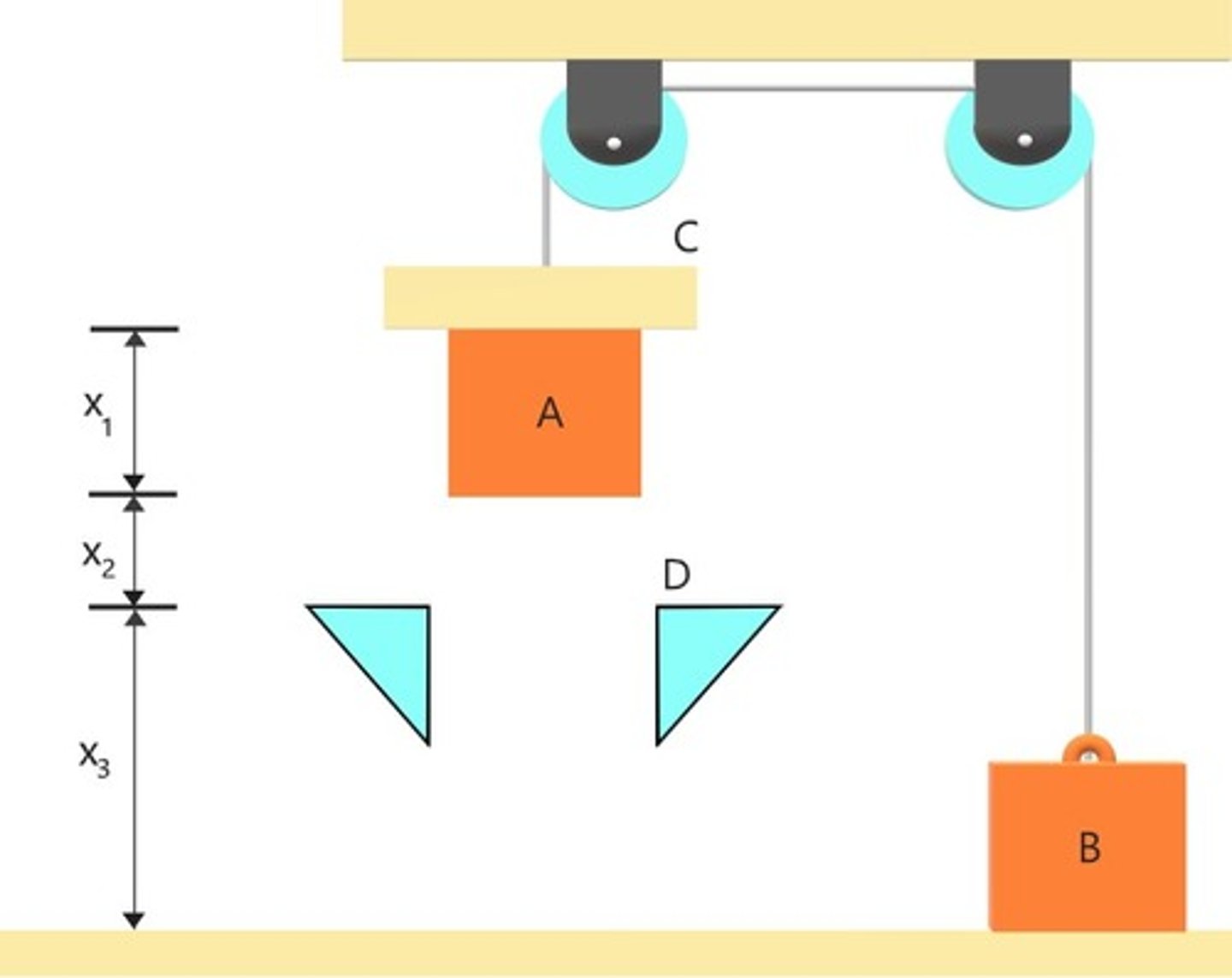
In the following problem, what is the relationship between the velocity of block A and the velocity of block B? Assume your coordinate system measures positive as away from the left hand side pulley.

3V_B+V_A=0

Suppose in this problem, you measure the distances from the fixed pulley located on the left hand side (just above C). Which one of the following statements is true:

Down and to the left are in the positive direction.

Consider the same set-up as before. What is the relationship between the velocity of the cable segment marked `C' to that of block B?

V_B + V_B + (V_B-V_C) =0

In this figure (same as before) what is the relationship between velocities of C and D (and possibly something else!). Pick the correct one

2V_B- V_D - V_C = 0

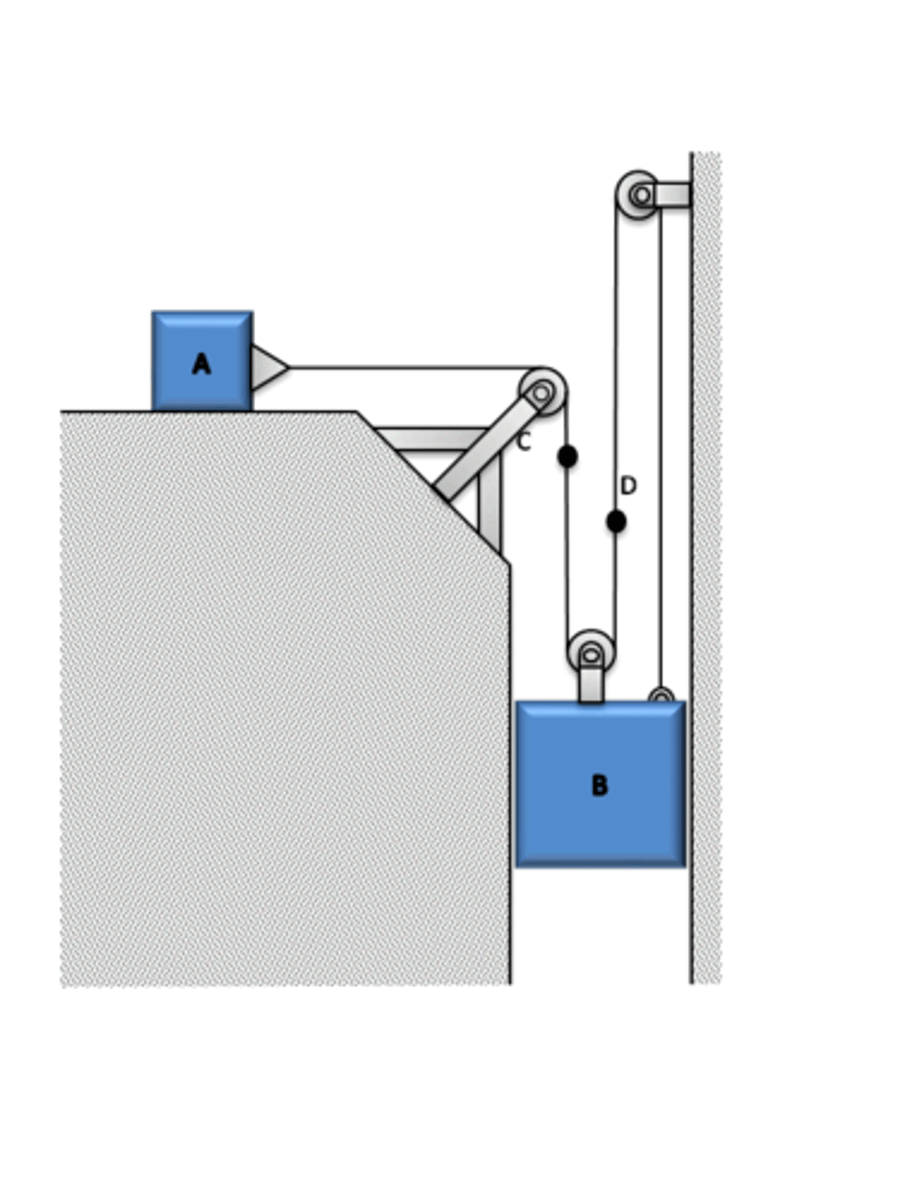
In this same problem, does it matter if distances are measured from the fixed pulley on the right or fixed pulley on the left?

It does not make a difference no matter what

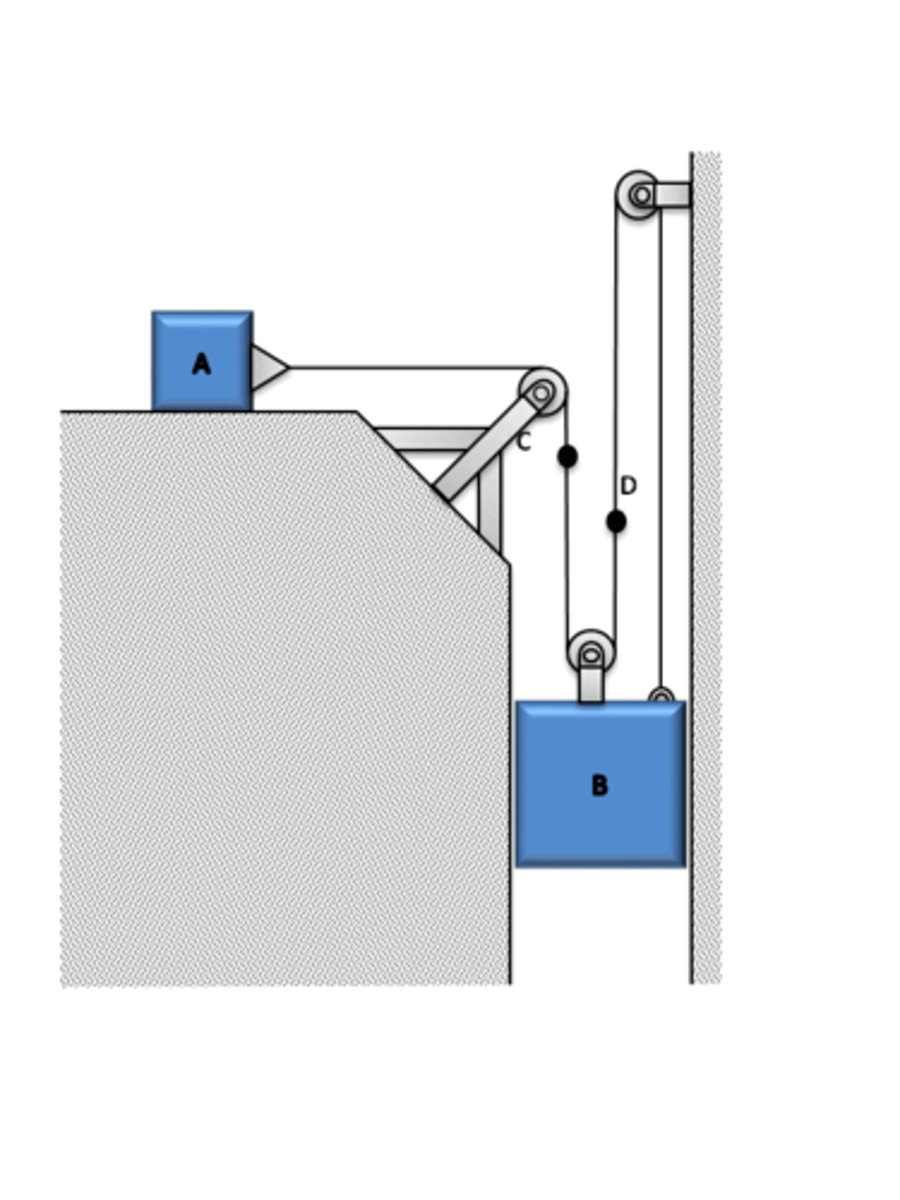
For this same problem, suppose we were measuring distance of B from the floor of the room. What would be the new relationship between the two blocks' velocities, if it were any different?

V_A - 3V_B=0

True or False: A vector that rotates has a derivative with respect to time, even if its length is constant.

True

True or false: The time derivative of a rotating unit vector is obtained by the following CROSS product: angular velocity VECTOR with which the unit vector rotates CROSS with the unit vector itself.

True

If position vector is d e_r, with constant d (i.e., constant distance but rotating around the center as e_r changes). Pick the right answer (here x-dot means time derivative of x)

Velocity is d (e_r-dot)

Suppose the position vector was r= d e_r , where theta is fixed (i.e., e_r does not rotate) but the length d is NOT constant. Which one of the following is correct

Velocity is (d-dot) e_r

In Polar coordinates, which one of the following statements is true

In a constant radius rotation, there is always a radial acceleration term

If motion is circular with constant radius, what is the so call `centrifugal acceleration'

it is the - r (\theta-dot)^2 in e_r direction

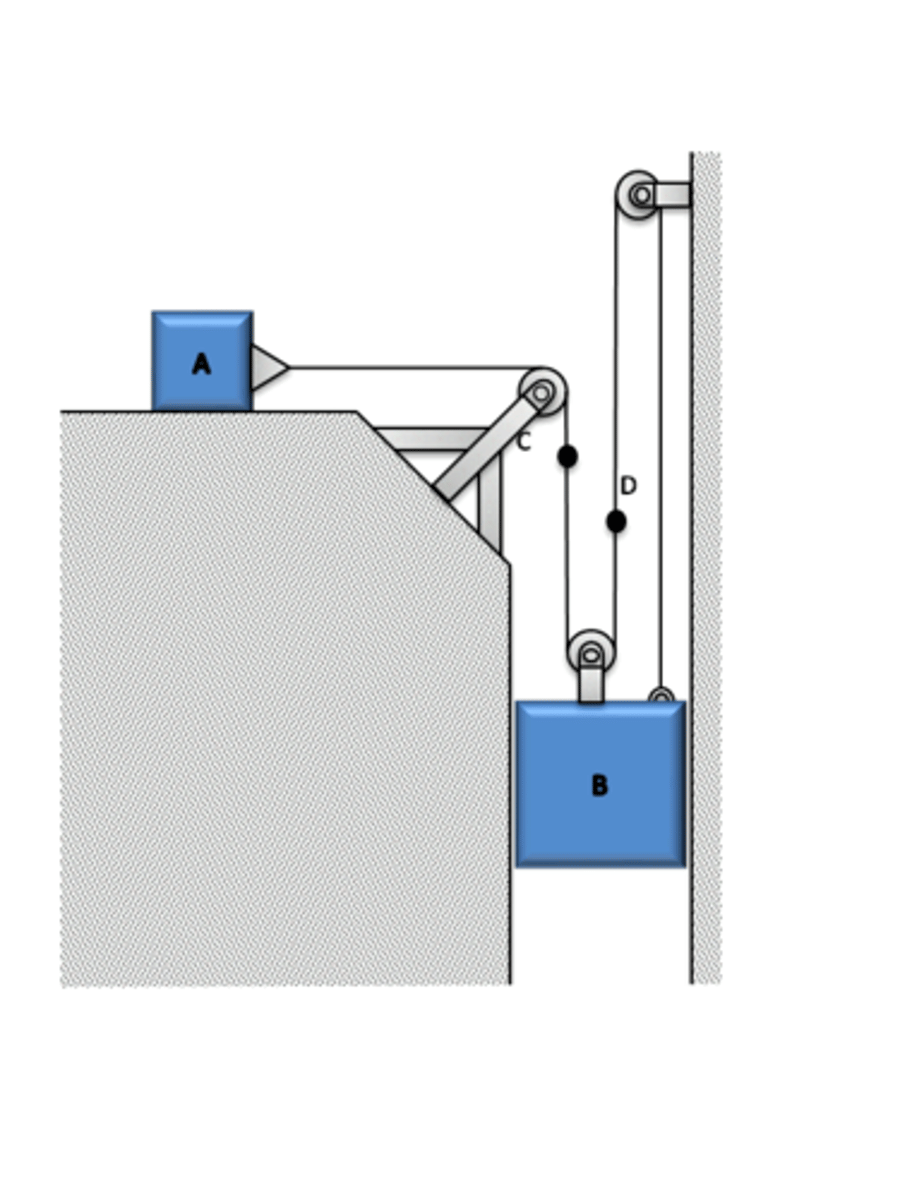
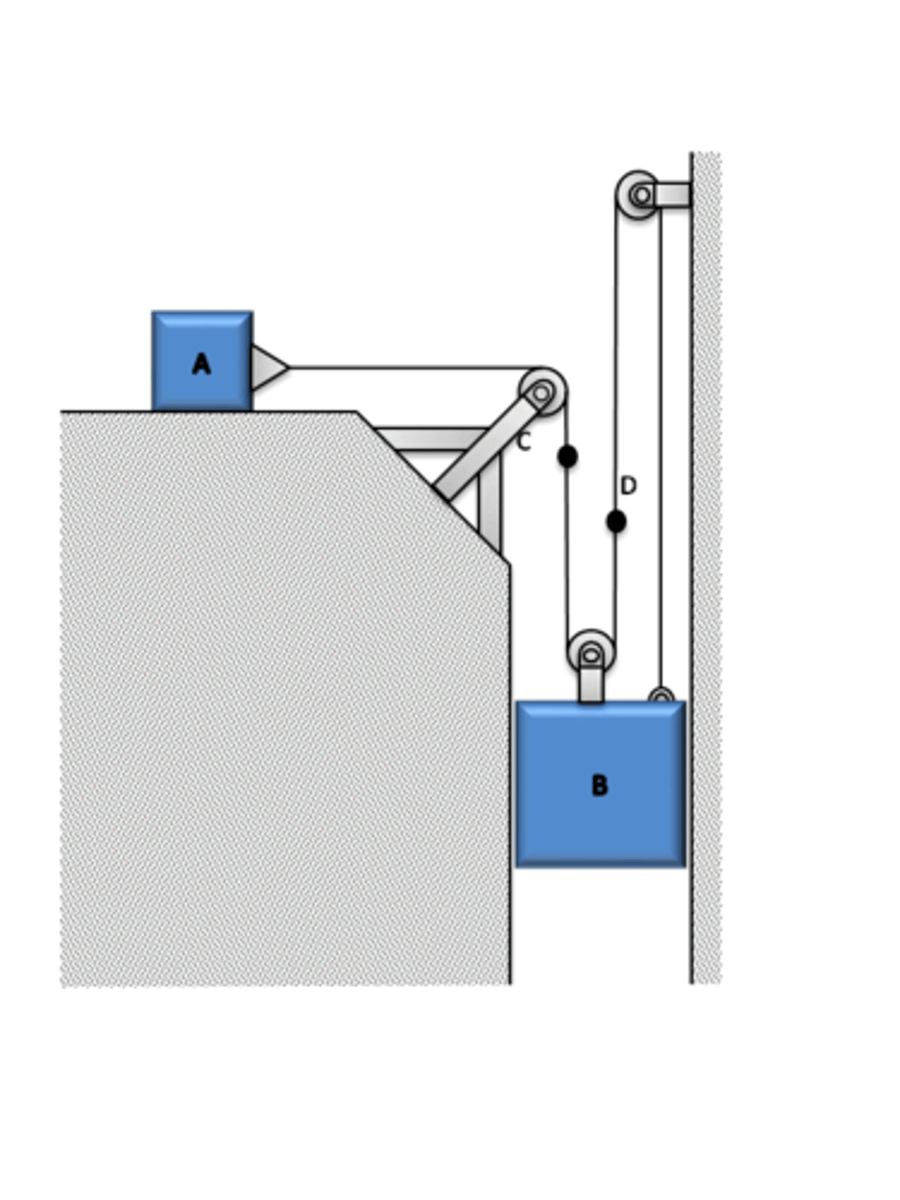
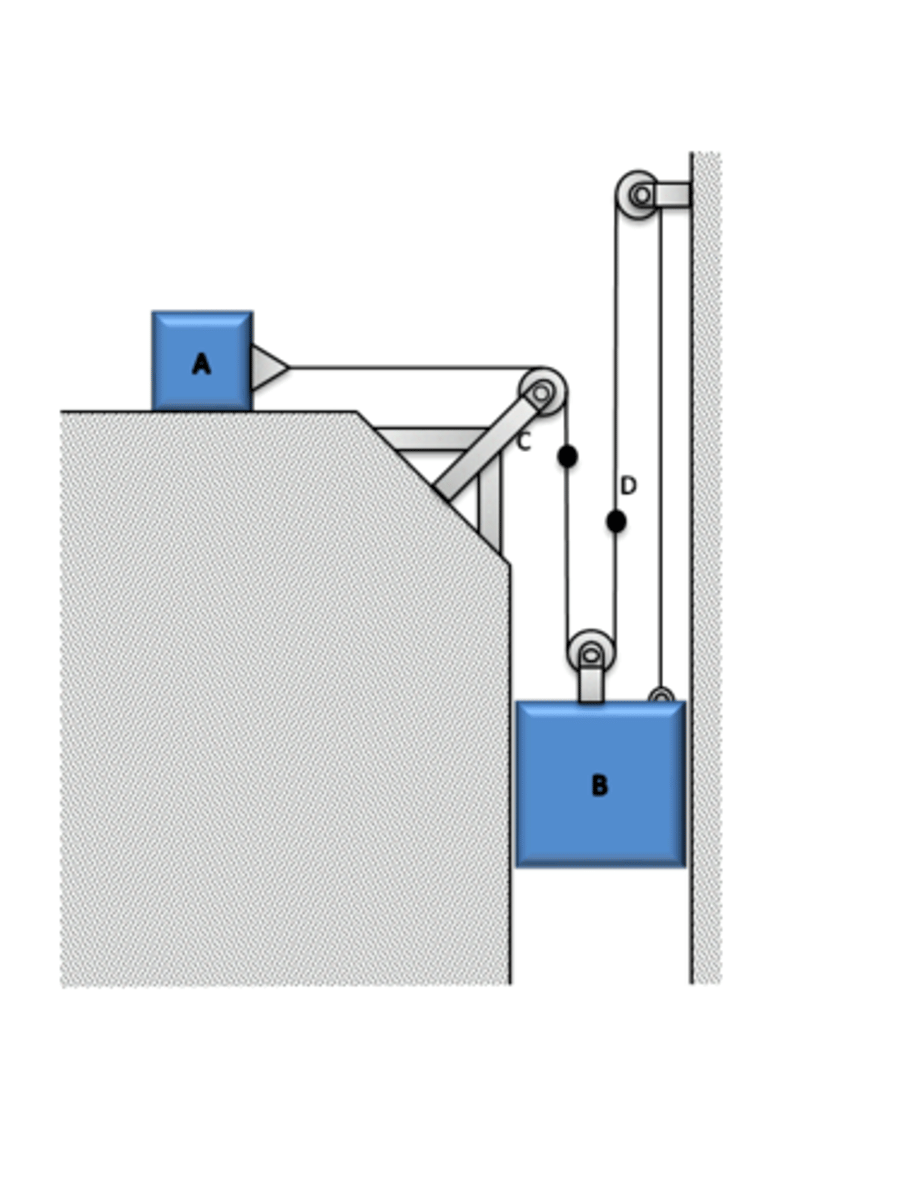
Which one of the following is correct?

2yA+2yB+yC=constant and (yD-yA)+(yD-yB)= constant

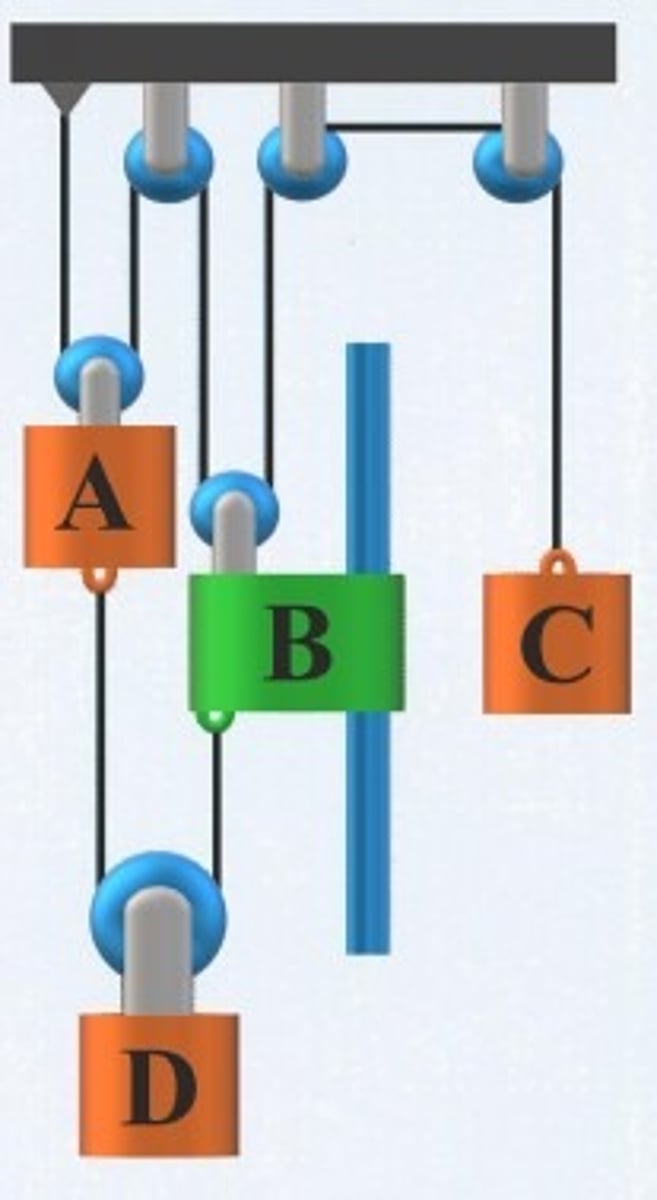
For the previous problem, express the acceleration of block C using its relative acceleration with respect to collar B, aC/B, and the acceleration of block D using its relative acceleration with respect to block A, aD/A.

aC=aC/B+aB,,aD=aD/aA

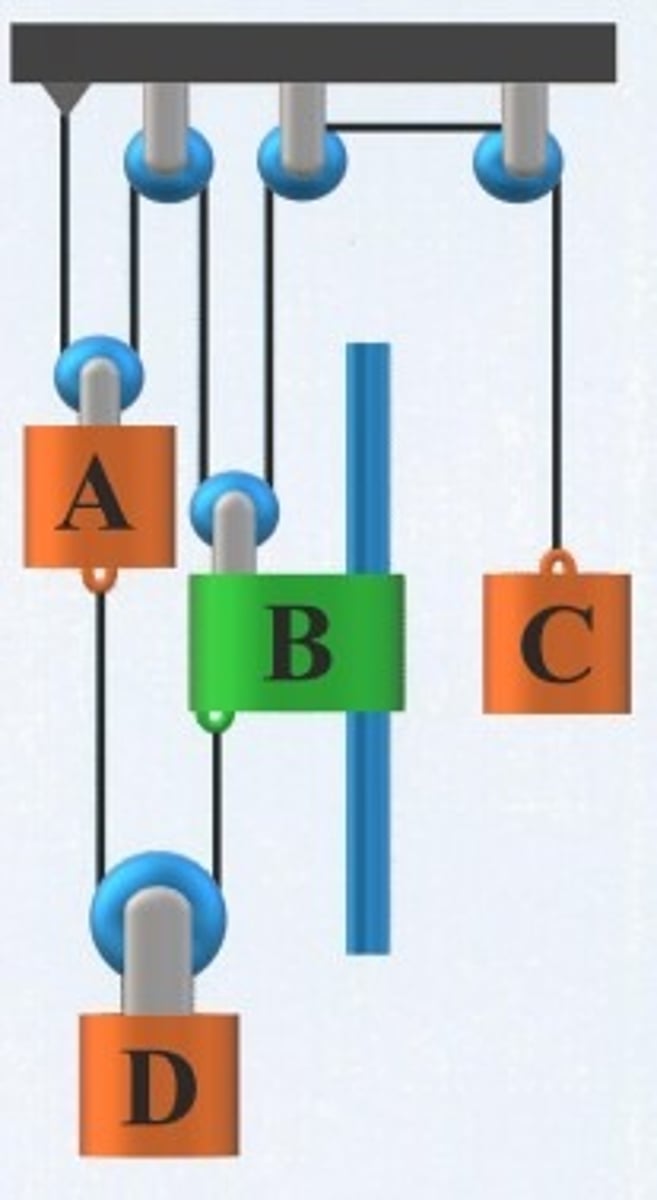
Can you write the length of the cable as 2xA+(xB−xA)=constant?

No

How would you express the length of the cable that connects B to the pulley on top of A?

xB/A

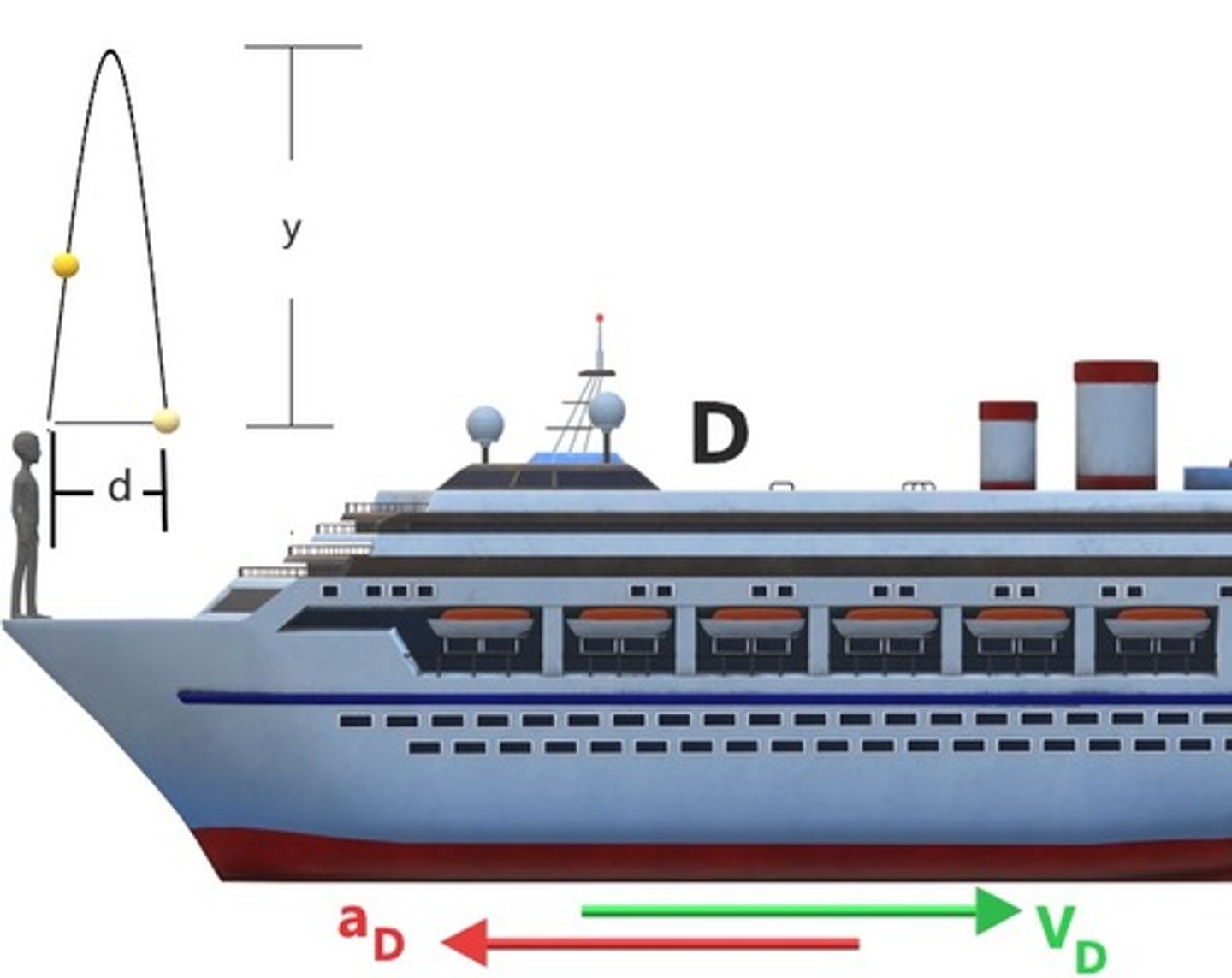
If the boy on the deck only throws the ball vertically upwards, does it come back to him if he stands where he is?

No it does not, boat slows in x-direction but ball does not

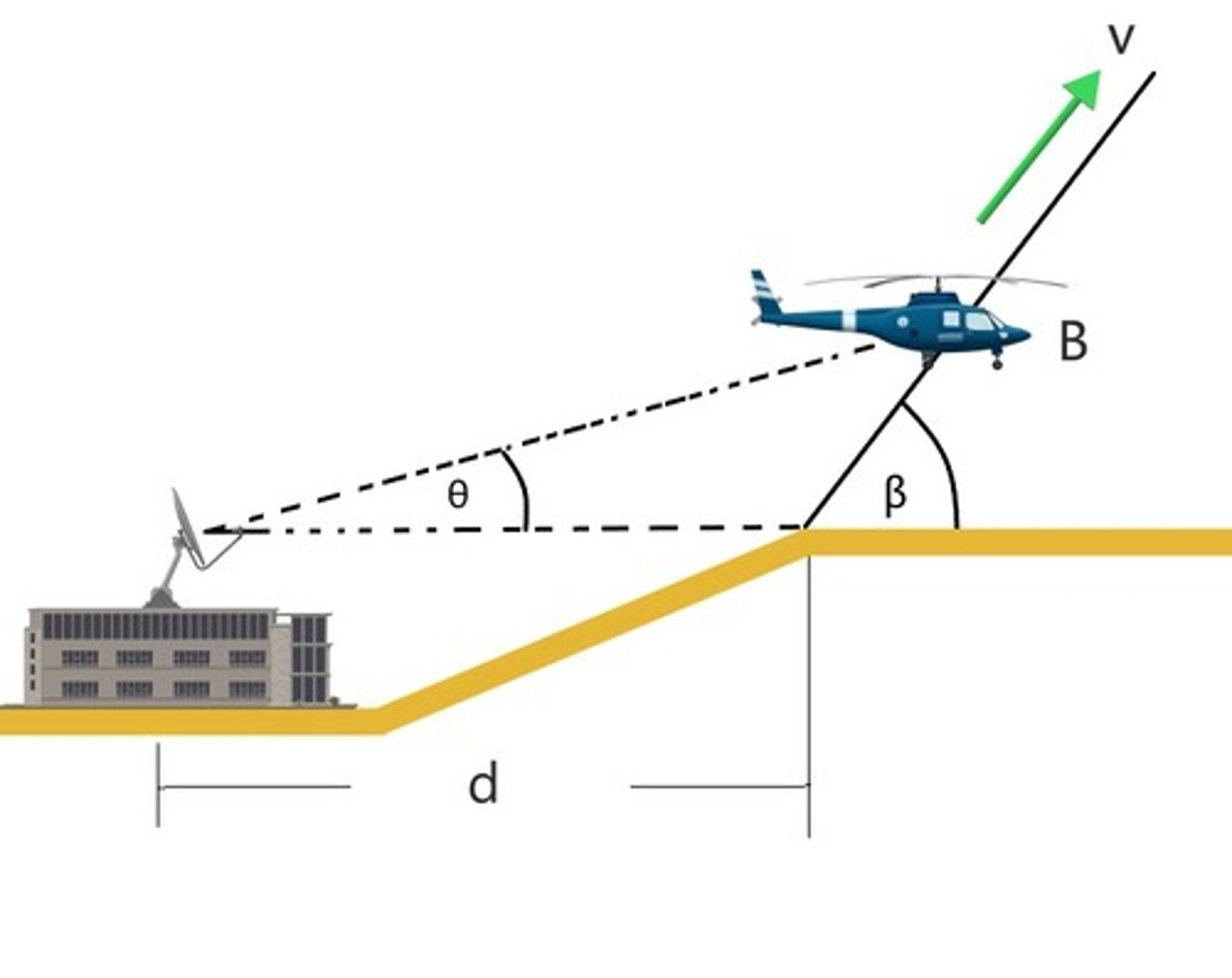
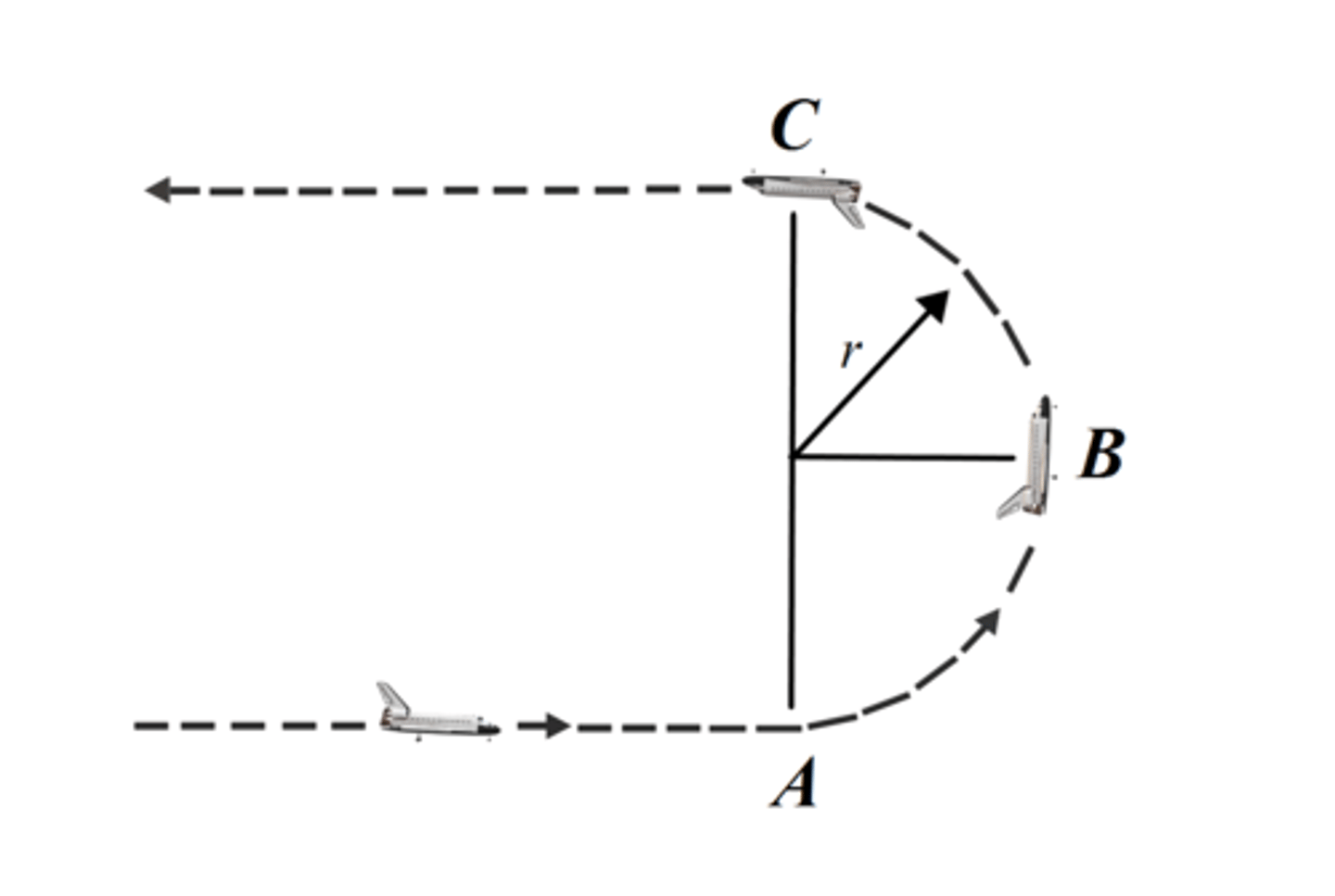
What is the velocity, vr and vθ, of the helicopter?

vr=vcos(β−θ)er,vθ=vsin(β−θ)eθ

In this problem, the polar coordinate is attached to the radar and the plane has a velocity of vo in the horizontal direction, at this instant since it is doing a large loop. Which expression is correct for the velocity in the polar coordinates

V=vocos⁡θer−vosin⁡θeθ

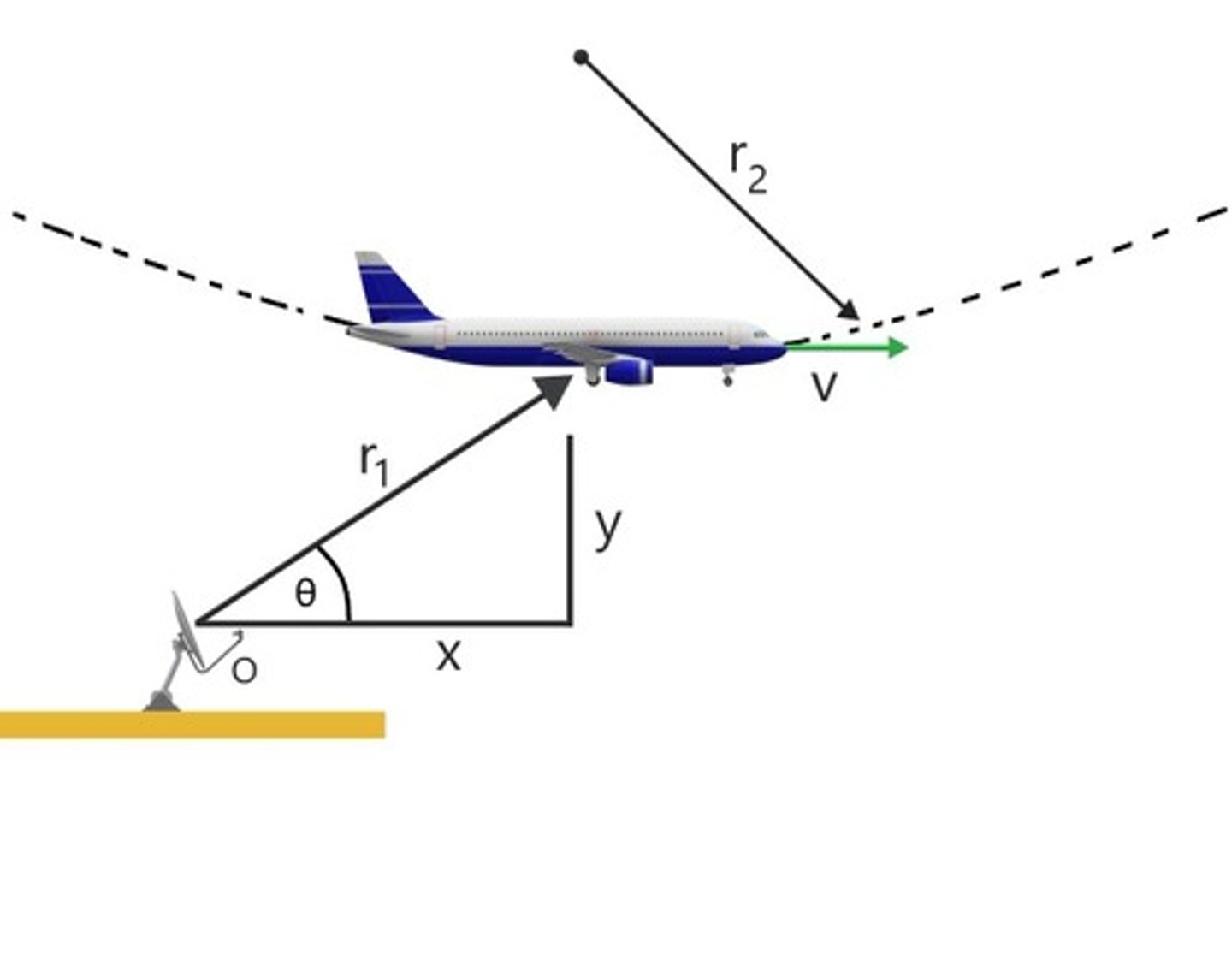
What are the general expressions for acceleration in the polar coordinates based on the radar location?

a=(r¨−rθ˙2)er+(rθ¨+2r˙θ˙)eθ

In Newton's second law pick the correct statement

F is sum of all external forces

True or False: Linear momentum in a direction is constant if external forces in that direction are zero

True

Which of the statements below apply to the famous 'centrifugal' force?

It is an 'inertial' force representing motion.

True or False: Normal forces are forces that the physical support provides to maintain the motion.

True

In a pendulum motion, consisting of a ball and a massless cable, which one of the following statements is correct

Tension is maximum at the bottom but can get to be zero above the 3 and 9 o clock positions

True or false: Friction always resists relative motion at the surface it operates.

True

Is the tension in case (2) the same as those in cases (1) or (3) - is the value 100 lb?

No, only in (2) the tension is 100 lb for sure

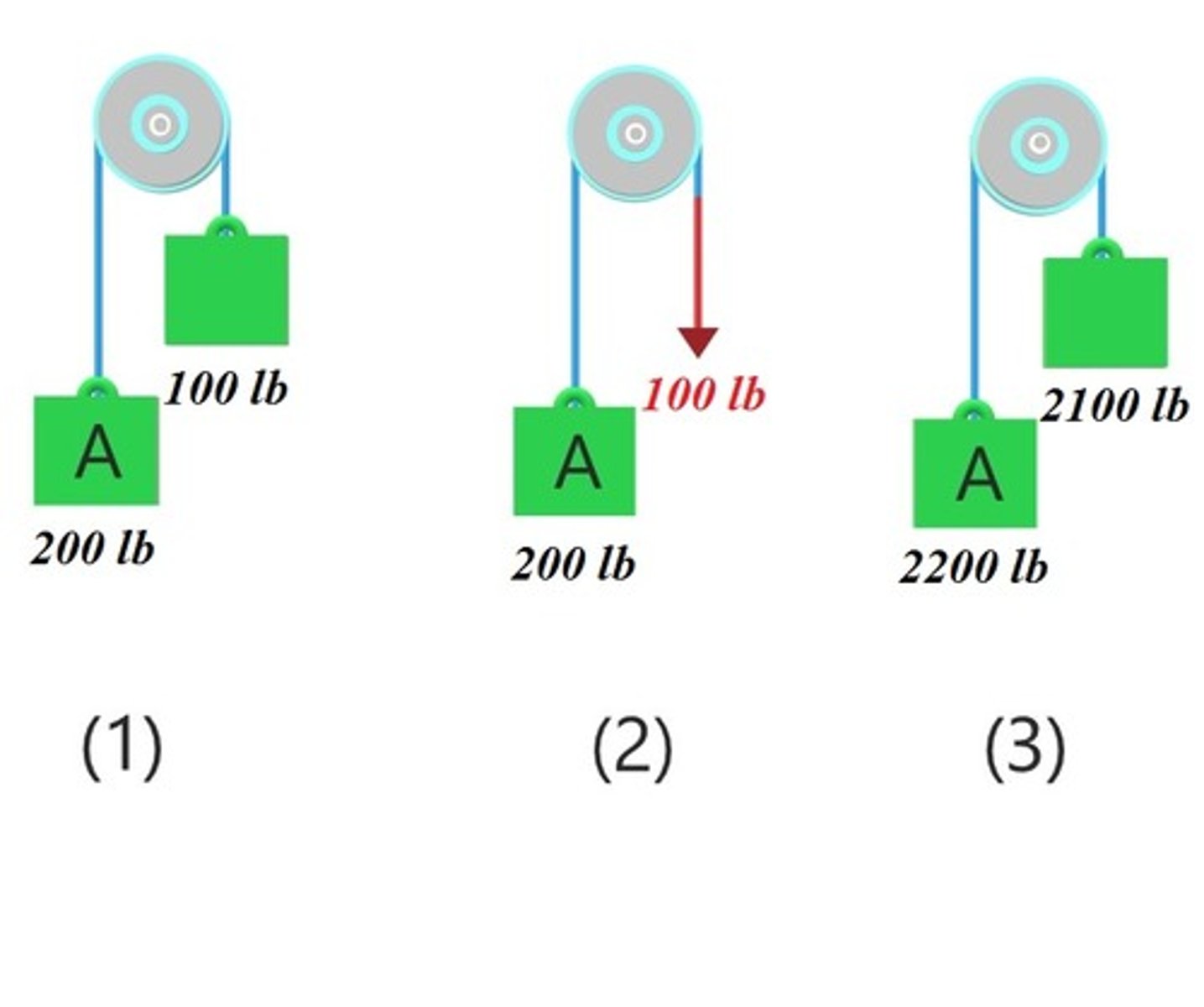
Even though scenario 1 and 3 have the same difference in weight between blocks A and B, will they move with the same acceleration? Why or why not?

Accelerations are not the same. The net force might be 100 lb, but the same force accelerates different amounts on mass in each problem.

Recall there is friction between B and A but not between A and the surface below it. Under what condition will the velocity/acceleration of bracket A and blocks B and C be the same?

When there is no slippage between bracket A and block B.

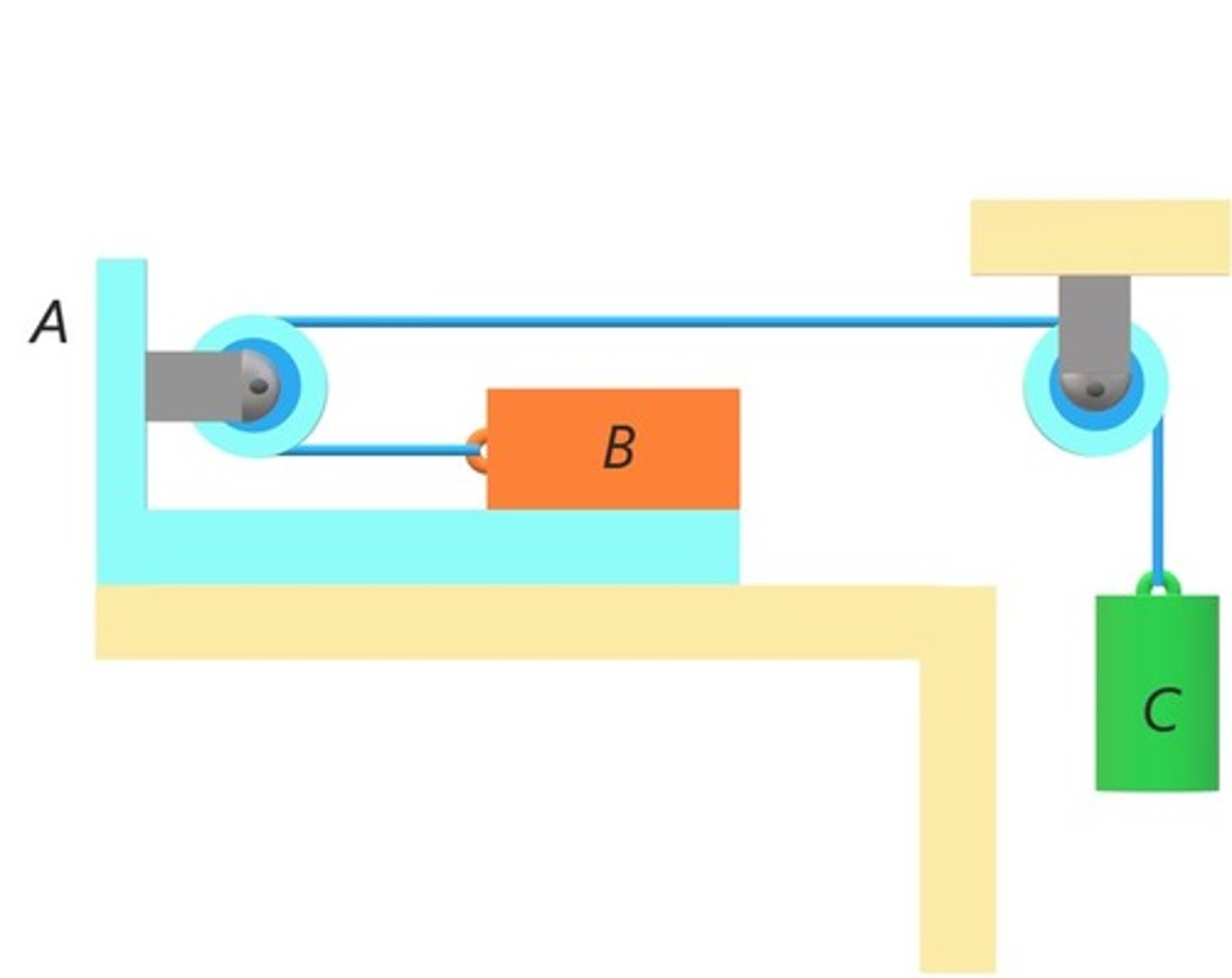
If there is no slippage between A and B, but motion starts for the assembly, what is the direction of motion of B?

To the right, with A since C can only go down, pulling A to the right

What is the direction of friction and cable tension acting on block B?

The friction force acting on block B is towards the right and the direction of tension is to the left

Which force is larger if B is not slipping on A but the whole assembly is moving? Why?

Friction, because B is moving to the right in absolute term.

Which one of the following explains why the slippage starts?

As C gets heavier, tension gets larger, the acceleration of A,B together goes higher, which required more friction force (to counter tension and provide force to move to the right). At some point, this force becomes equal or bigger than F=μsN and slippage starts

Given TAC(sin15∘)=mg sin45∘−mv2ρ cos45∘ and TBCsin15∘=mv2ρcos30∘−mgsin30∘, how does increasing the velocity of the sphere affect the tension in cable AC and BC?

We see that increasing the velocity increases the tension in cable BC and reduces the tension in AC, until tension in AC becomes zero

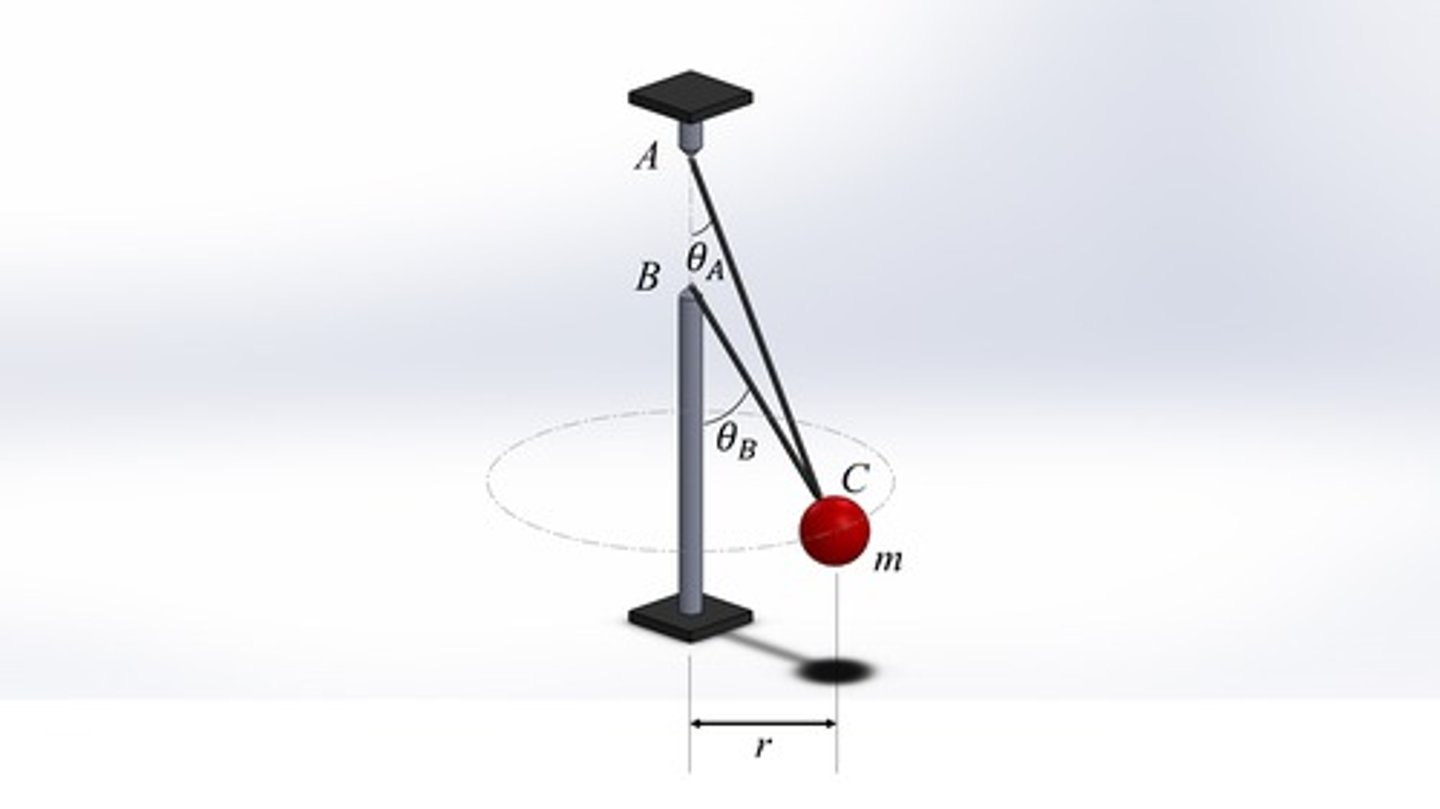
What happens if we increase or decrease the velocity by a lot?

If v is increased a lot, tension in AC become zero and the ball moves up, supported by BC only. If reduced a lot, tension in BC become zero first and then ball moved down supported by AC only

What is the direction of the normal forces on the pilot at points A and C?

Up and down, respectively

Are linear momentum and or energy conserved? Why or why not?

Neither is conserved.

The derivative of angular momentum is r x F, torque. Is there a direction (i, j, or k) in which r x F will always have a zero component?

The only torque is due to gravity in j, thus r x F is never in j, thus j component of angular momentum is conserved

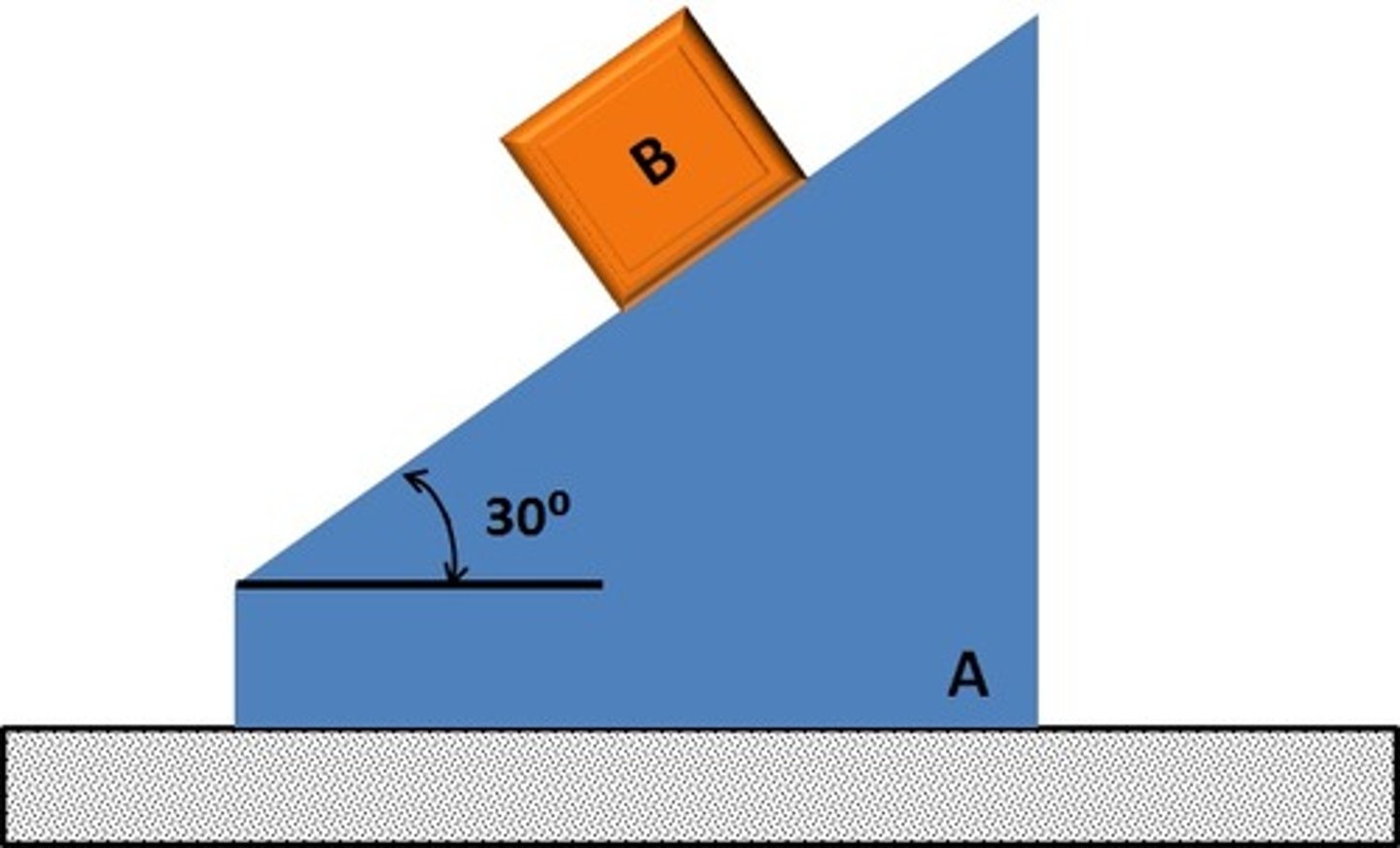
Here the `system' denoted A and B. Block A is free to move on the surface below (ie no friction between A and the ground). Pick the correct two statements:

1. Relative velocity of A with respect to the center of gravity of the system is in upward and to the right

2. Center of gravity of the system does not have any velocity in x-direction

Pick the correct two statements: ignore friction between A and B

1. Internal forces do not do `net' work in this system

2. Gravity does positive work on this system

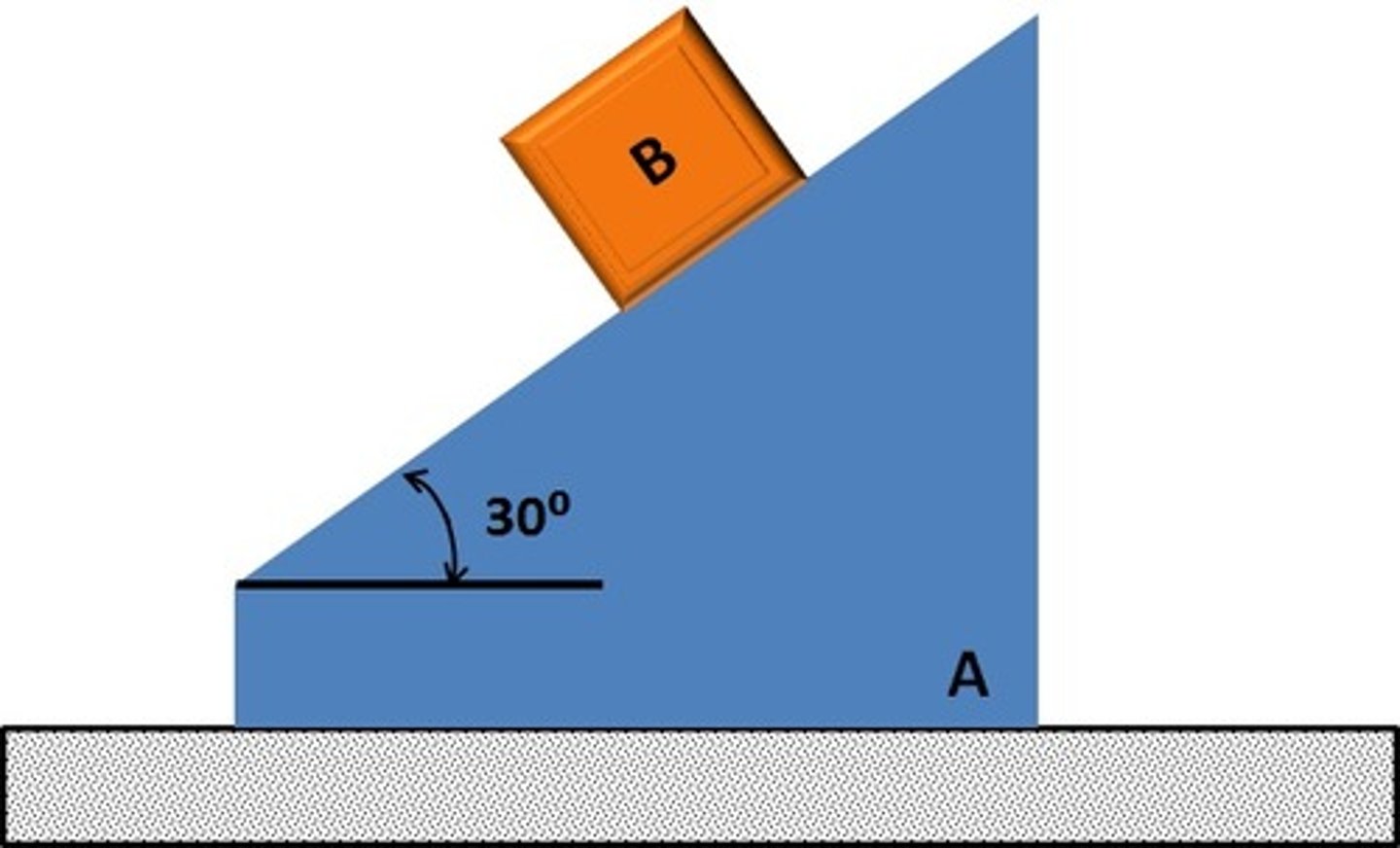
Pick the correct statement: This time THERE IS friction between A and B

Internal forces do `net' work in this system

For a system of particle, what is relationship between absolute position vector and position vector from center of mass, respectively r and r'

A. r=r′

B. ri=rG+ri′

C. ri′=rG+ri

B

Which of the following is good definition of center of mass

A. ∑miri=0

B. ∑miri′=0

C. mtotalrG=∑miri

D. mtotalri′=∑miri′

B and C

Which statement is true about the the right hand side of the following equation

mtotalaG=∑Fi

Sum of all external forces only

The two identical masses (connected with a compressed spring) are traveling to the right with a velocity of v_o. The string that holds the spring compressed breaks. Pick the two correct statements

1. The magnitude of the momenta (momentums!) of the two masses are the same in the Y direction

2. The center of gravity of the system will continue to move to the right with v_o

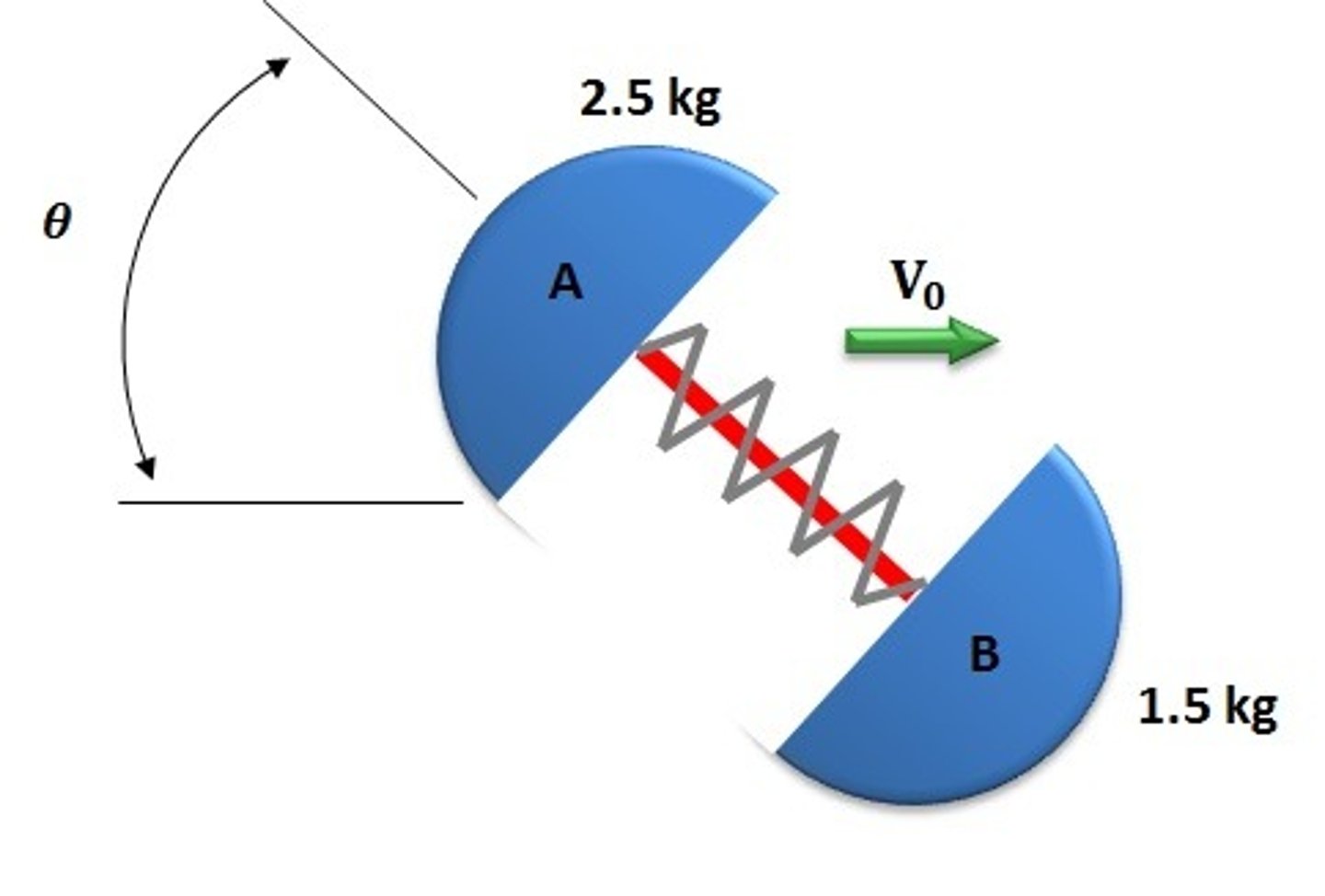
Pick 2.

1. The spring force does work on both masses, but not necessarily by equal amounts

2. The spring force does do net work on the system of two masses

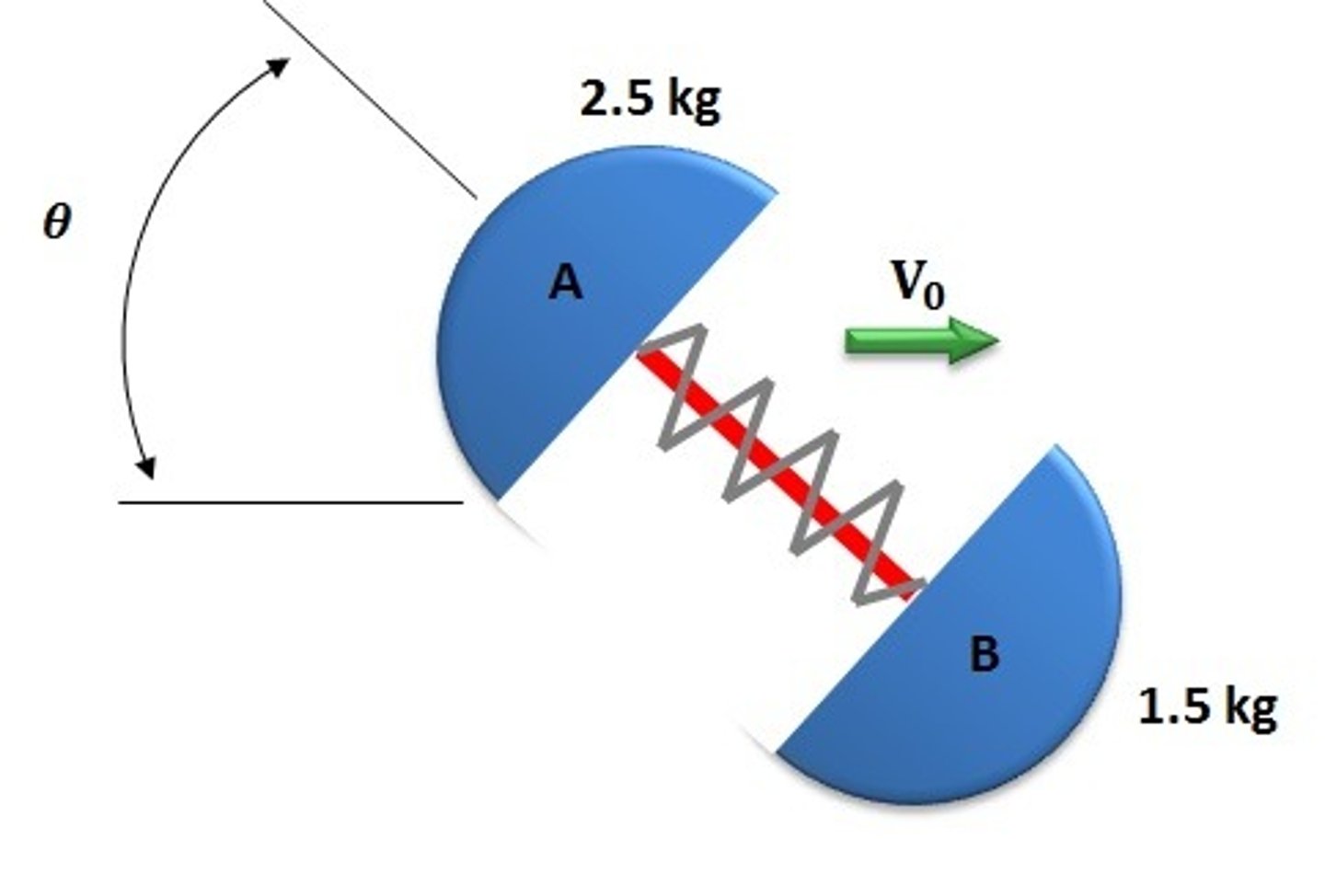
Pick 2

1. Linear momentum of this system is conserved

2. Angular momentum of this system, around the center of gravity or any other point, is constant

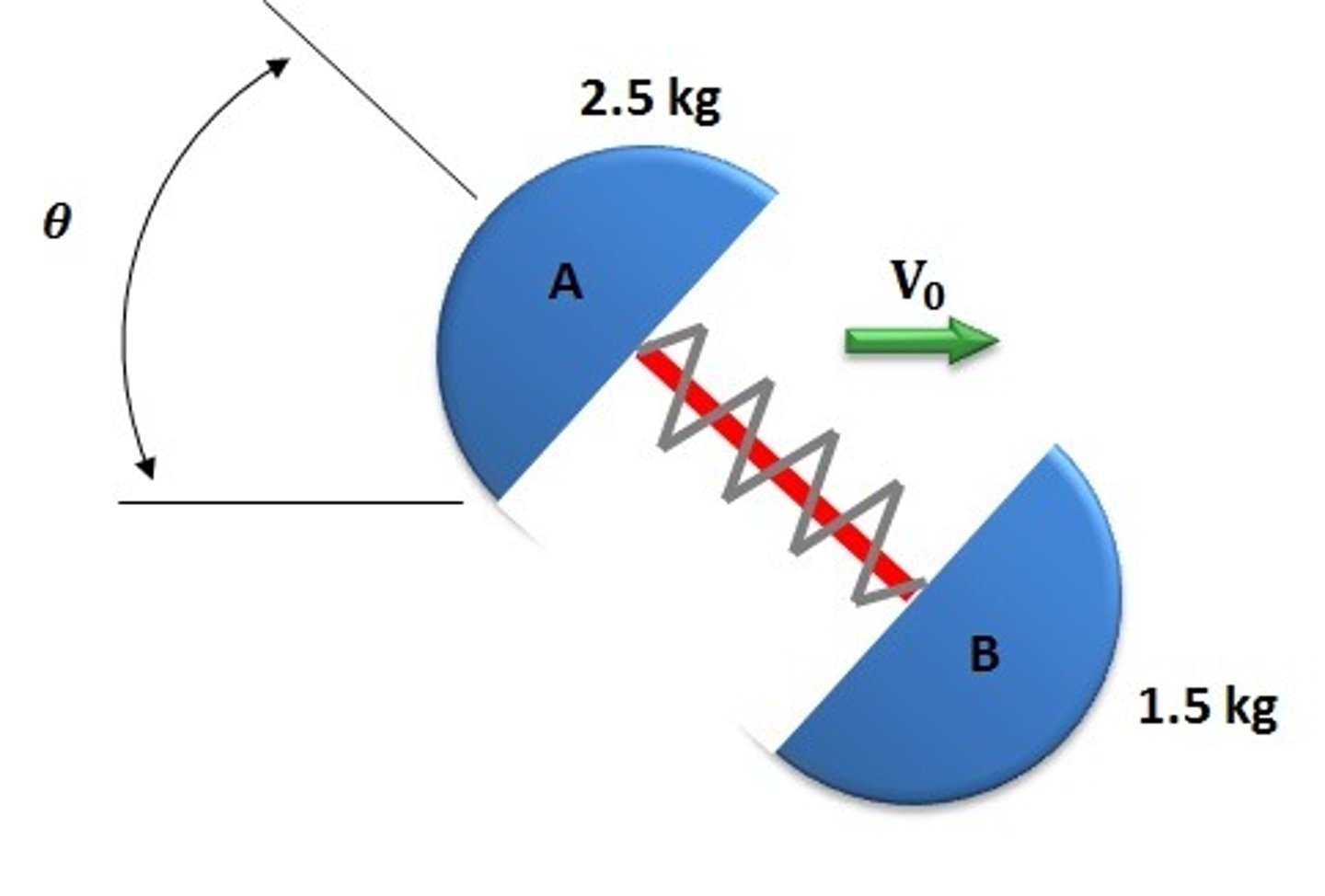
which of the following statements are correct

A. L=∑mivi

B. mtotalvG=∑mivi

C. L=∑mivi′

D. vG=∑mivi

A and B

In a system of particle, when we have sum of the forces in some direction is zero, it means that

Velocity of the center of mass in that direction is constant

For angular momentum, we have

ddtHo=Mo

what is the right hand side

Sum of the moments of external forces , internal forces cancel each other

consider the following two possible/candidate definitions for angular momentum about the mass center HG

A: HG=∑ri×mivi′

B: HG=∑ri′×mivi′

Only B is correct

How come internal forces do not show up in the angular momentum relationships (e.g., ddtHG=MG )

They do not show up: equal and opposite, their moments always cancel

In the work-energy approach, what role do internal forces play

They might do `net' work and we have to be careful since we might have to take them into account

In this problem, we release B from this position, both cart and mass from rest

The center of the gravity of the system has non-zero y-dir velocity

True or false: The normal force from the support to cart is not constant

True

True or false: The total mechanical energy is not constant

True

In this problem, we release B from this position WHILE HOLDING the cart and then release the cart once A gets to the 6 o'clock position

1. The center of the gravity of the system has nonzero y-dir velocity

2. The center of the gravity of the system has nonzero x-dir. velocity

Is the tension in the cable constant?

No.

Is the normal force from the support to the cart constant?

No.

Pick two

1. Cable does not do net work on the system

2. The total mechanical energy is constant

In the problem with 2 balls connected by a massless cable (with one of the balls given initial velocity), which quantity is conserved

A. Angular momentum about O, the origin of the global coordinate system

B. Angular momentum about G (system's center of mass)

C. Linear Momentum

D. Energy

All

In the problem with two masses connected by a massless cable when one mass is given initial velocity, what is y-component of the velocity of A and B, when they are in 12 & 6 o'clock position?

Zero: max and min displacement in y-direction, its derivative (velocity) is zero

In the same two balls connect .......

Does the cable connecting them work?

Yes, it works on both but positive and negative work cancel one another

In this problem, the bullet hits the box, the box starts sliding on the cart and at some point, while they are both moving, they hit the left hand side wall. There is friction between the box and the cart. The system considered in this case is the cart, the bullet, and the box.

During this whole process linear momentum is constant ONLY if there is no friction between the ground and the cart

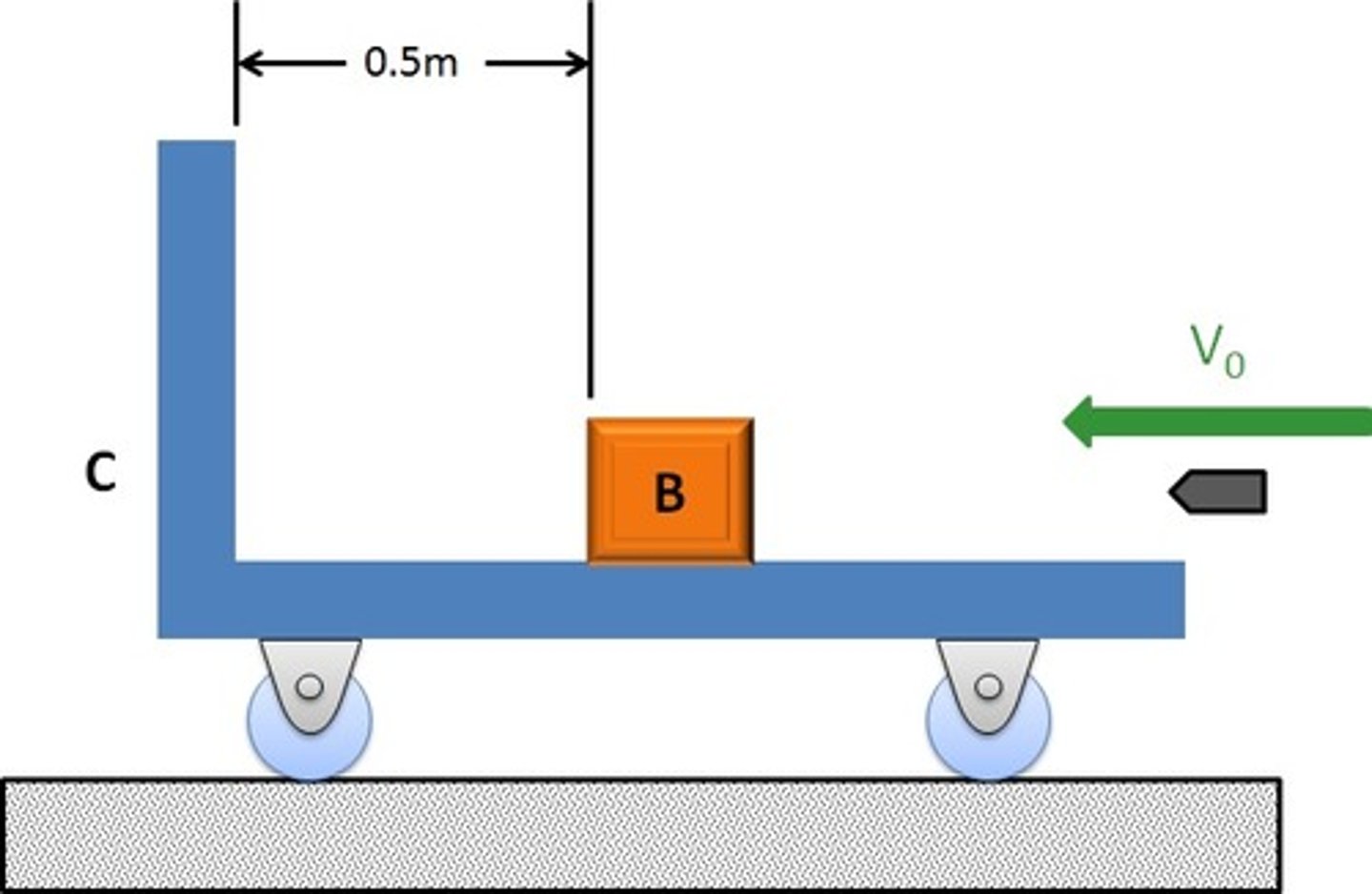
True or false: During the collision, we can ignore friction as long as mu is finite.

True

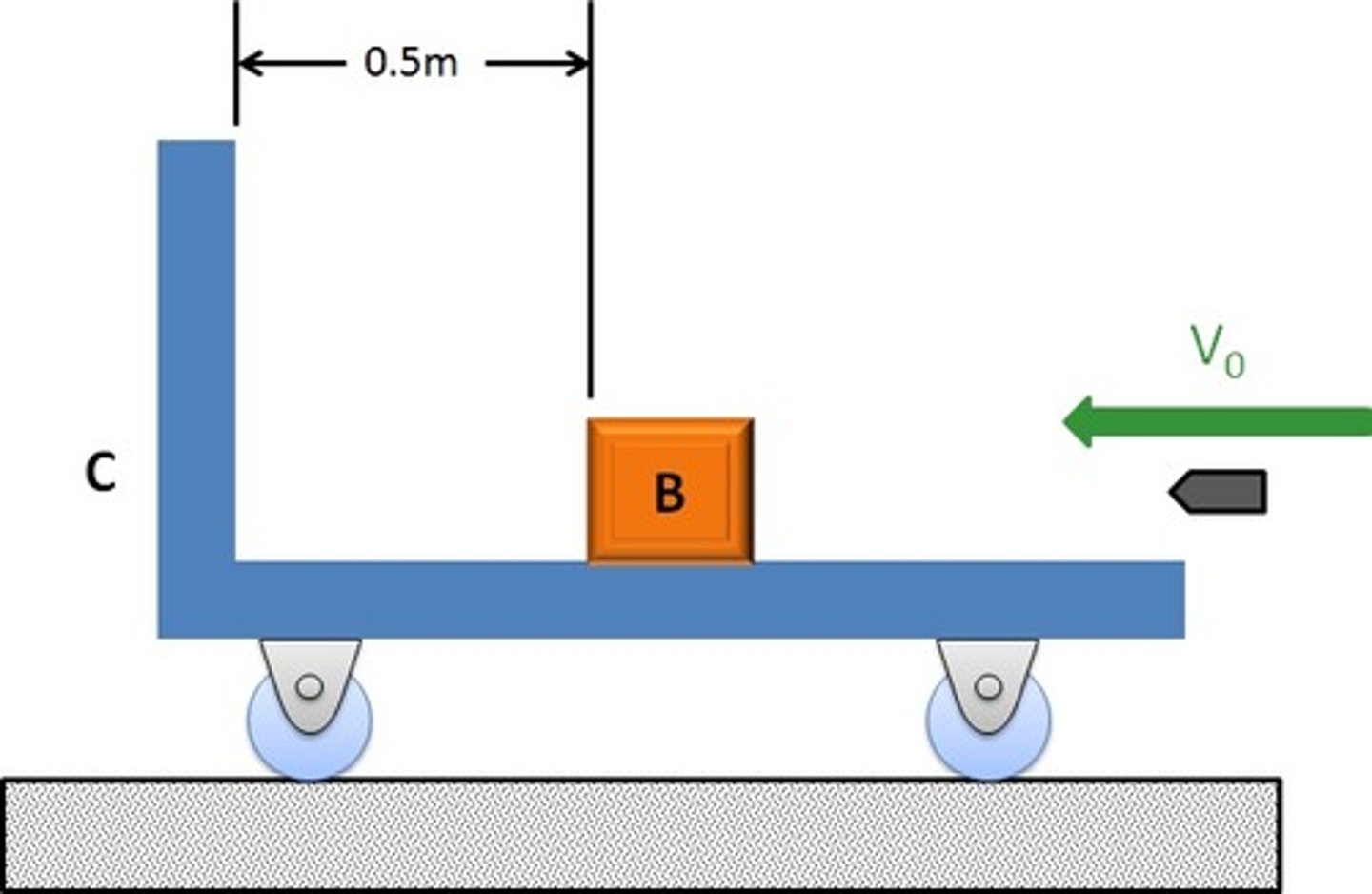
True or false: Friction (between cart and box) does net work.

True

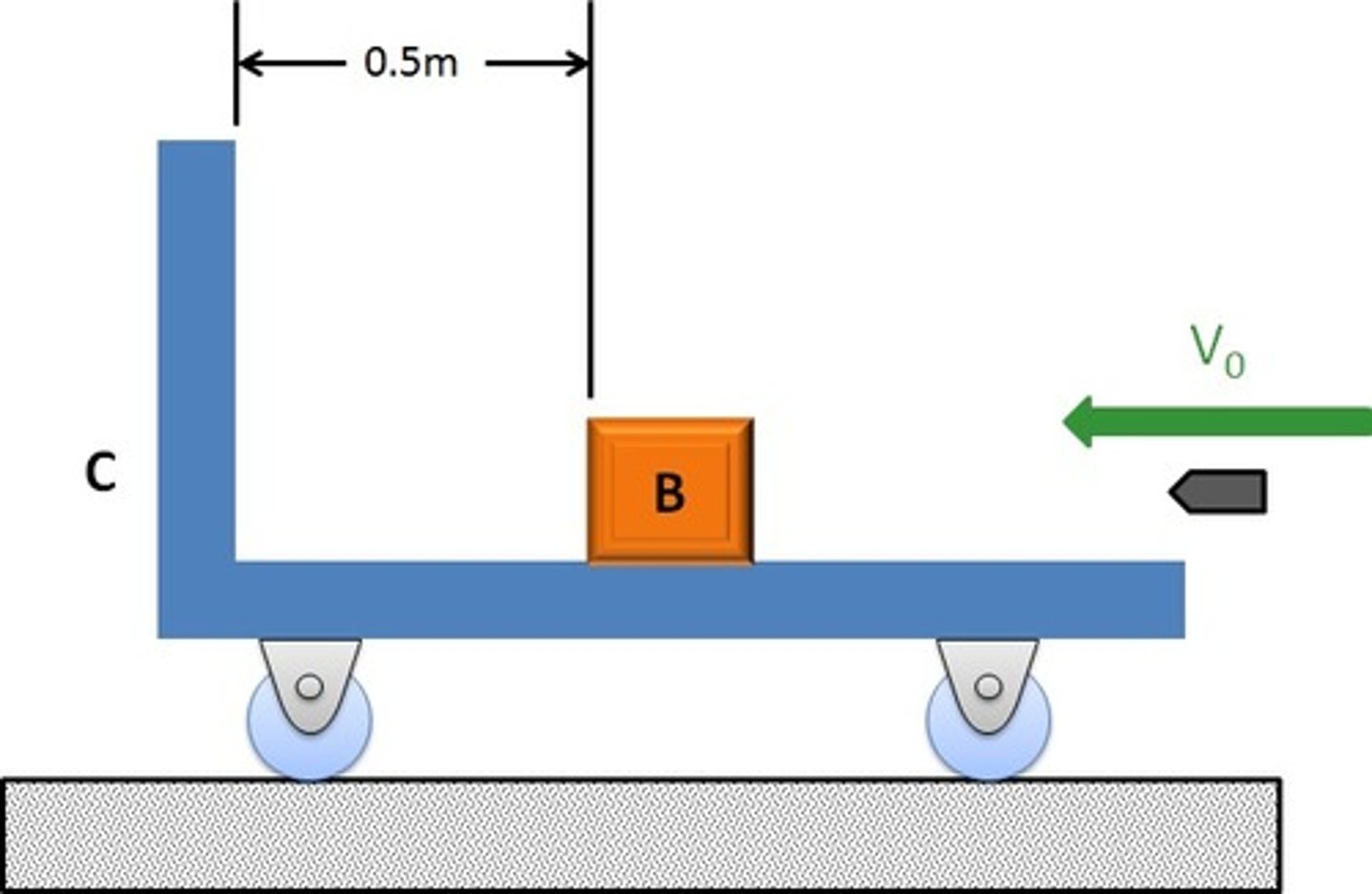
What is the relationship between accelerations of A and B?

Acceleration of A is twice the acceleration of B

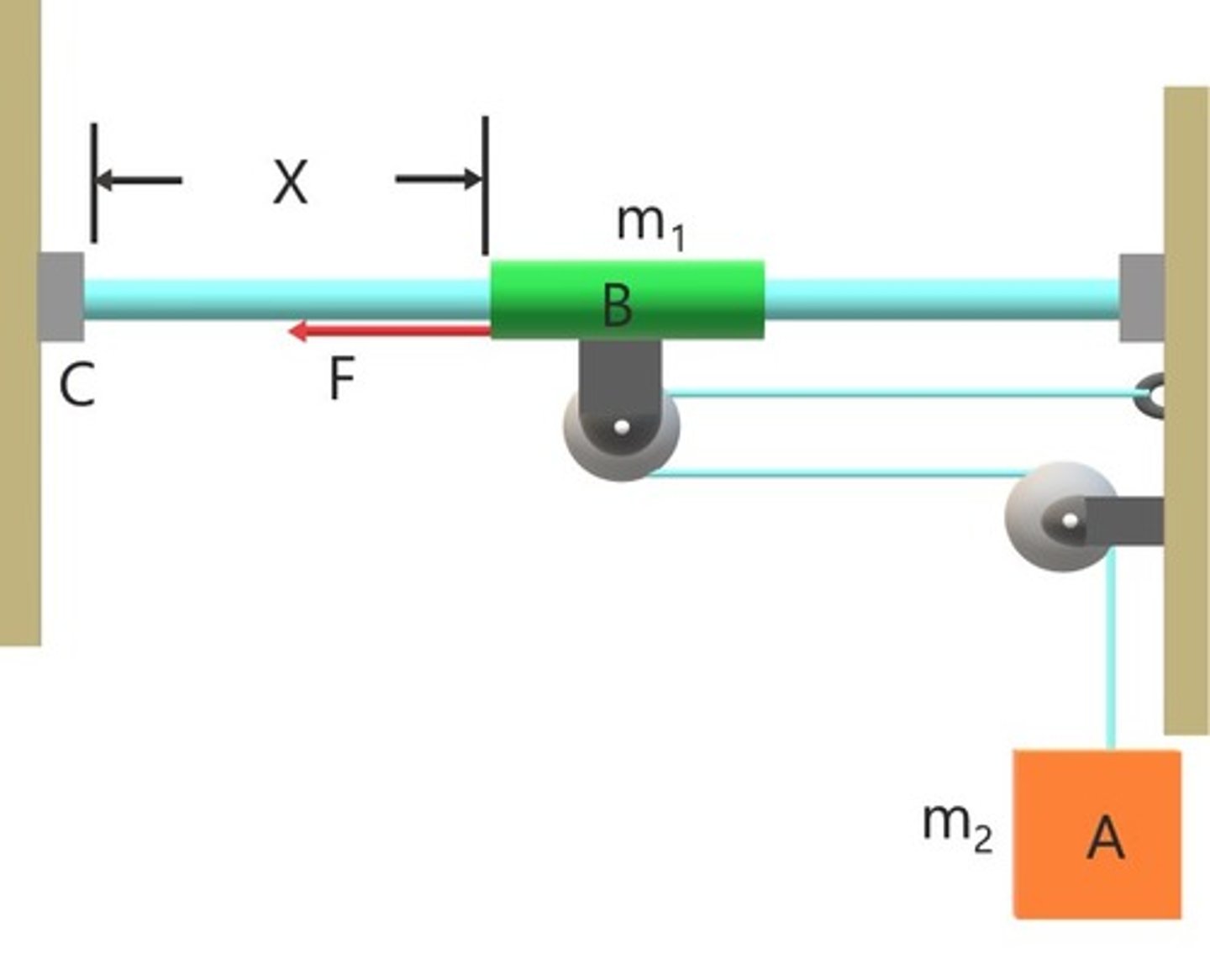
Can conservation of energy be applied to the whole motion, from start to end?

No, collision at D might not be perfectly elastic.

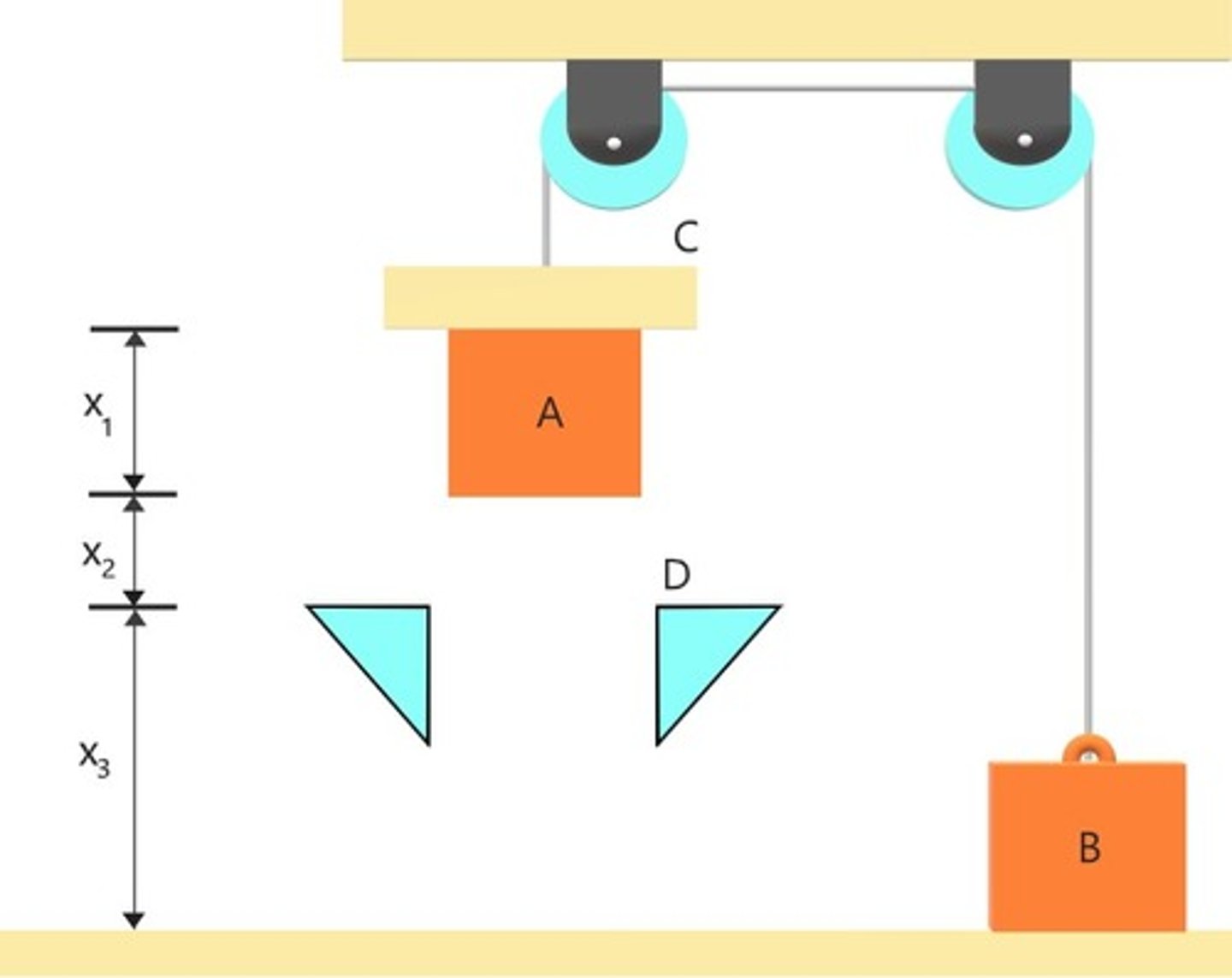
For a system comprising of A and B only, is the energy conserved throughout the whole process?

No, weight of C acts as an external force

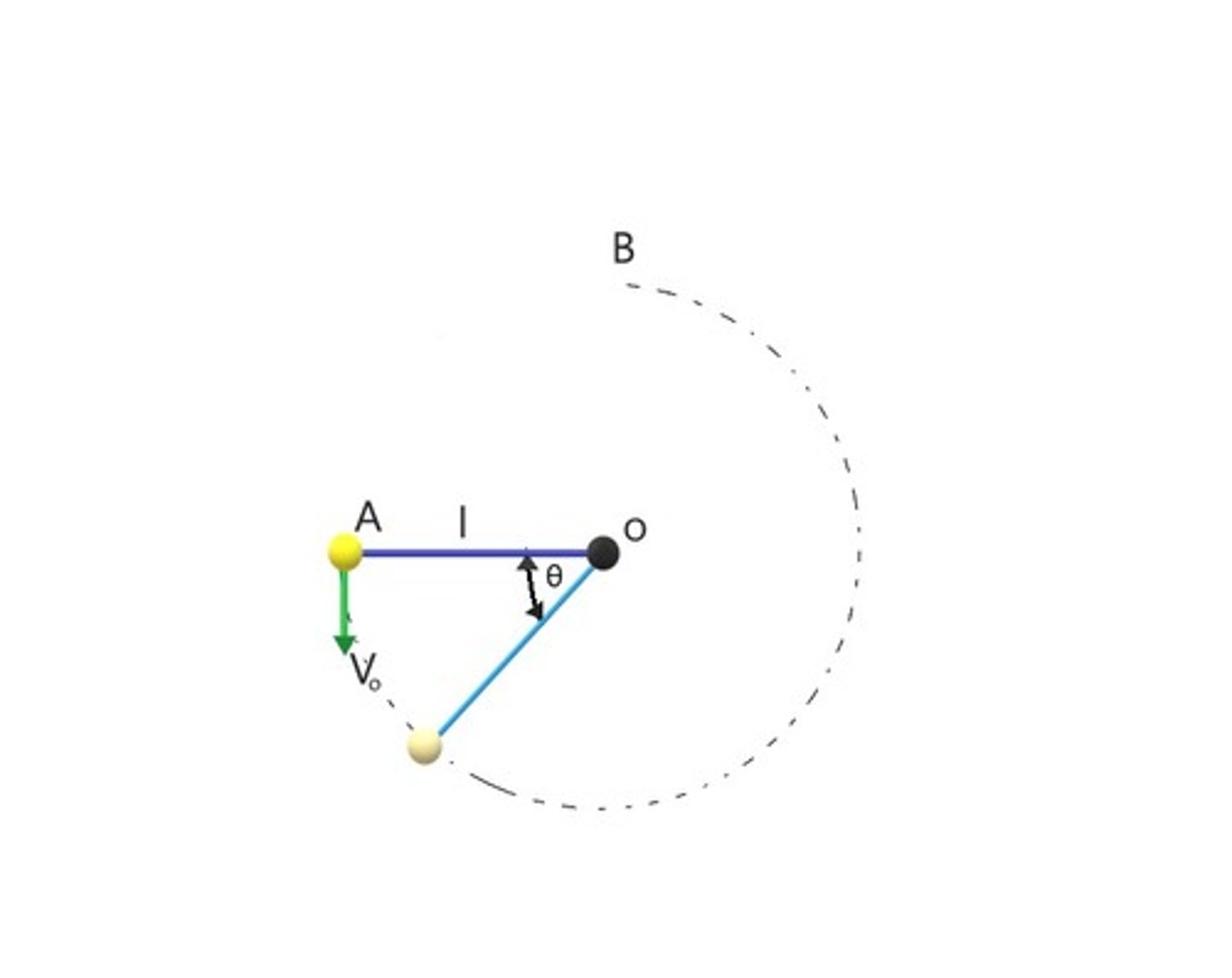
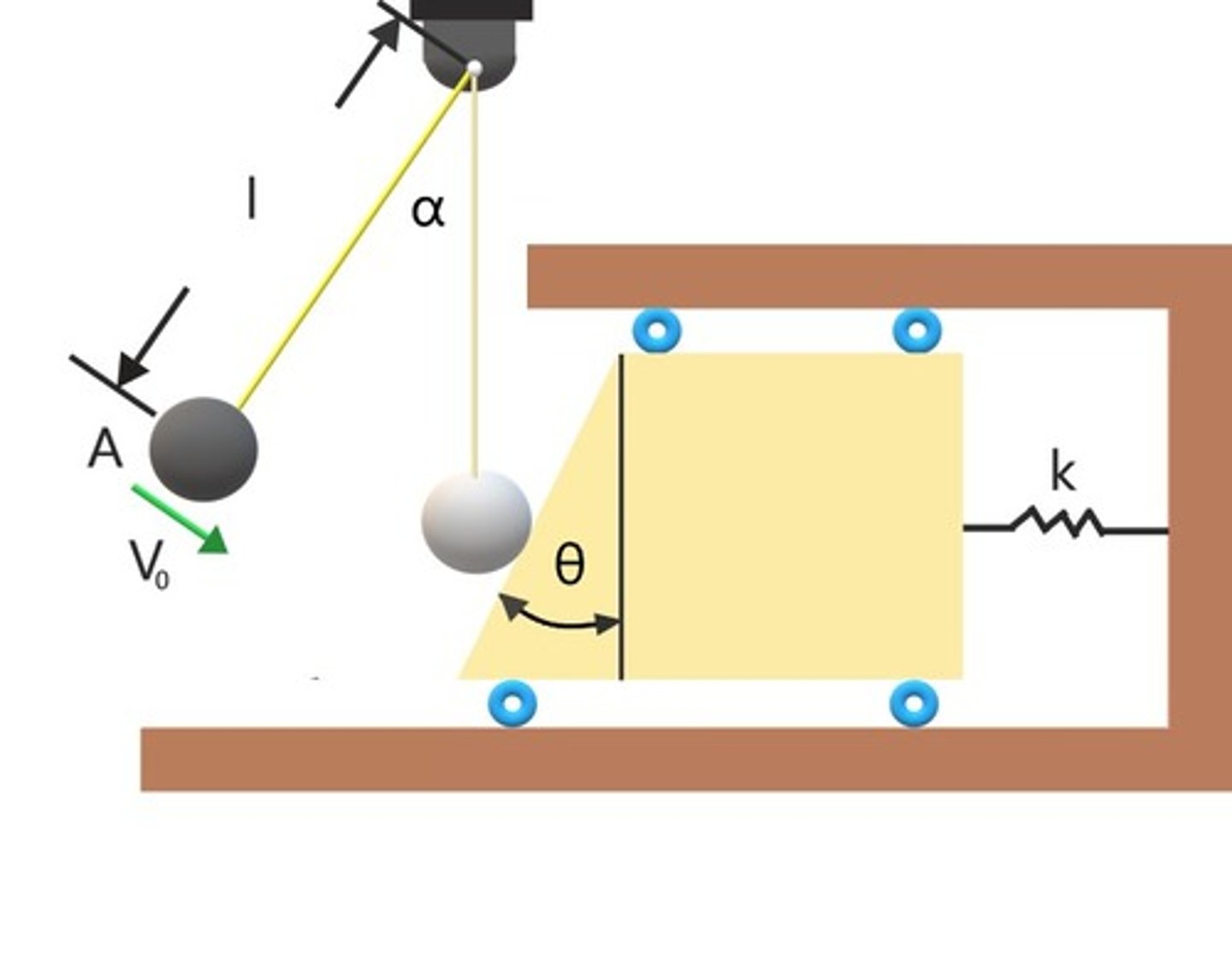
If the pendulum never makes it to Point B. Pick the right answer considering the following possible scenarios

a) Definitely the cable breaks between 6 o’clock and 3 o’clock positions

b) The ball will stop climbing when it has zero speed

c) The ball will fall off the circular path when tension in cable is zero

d) Cable break between 9 o’clock position and 6 o’clock position

it can be either c or d

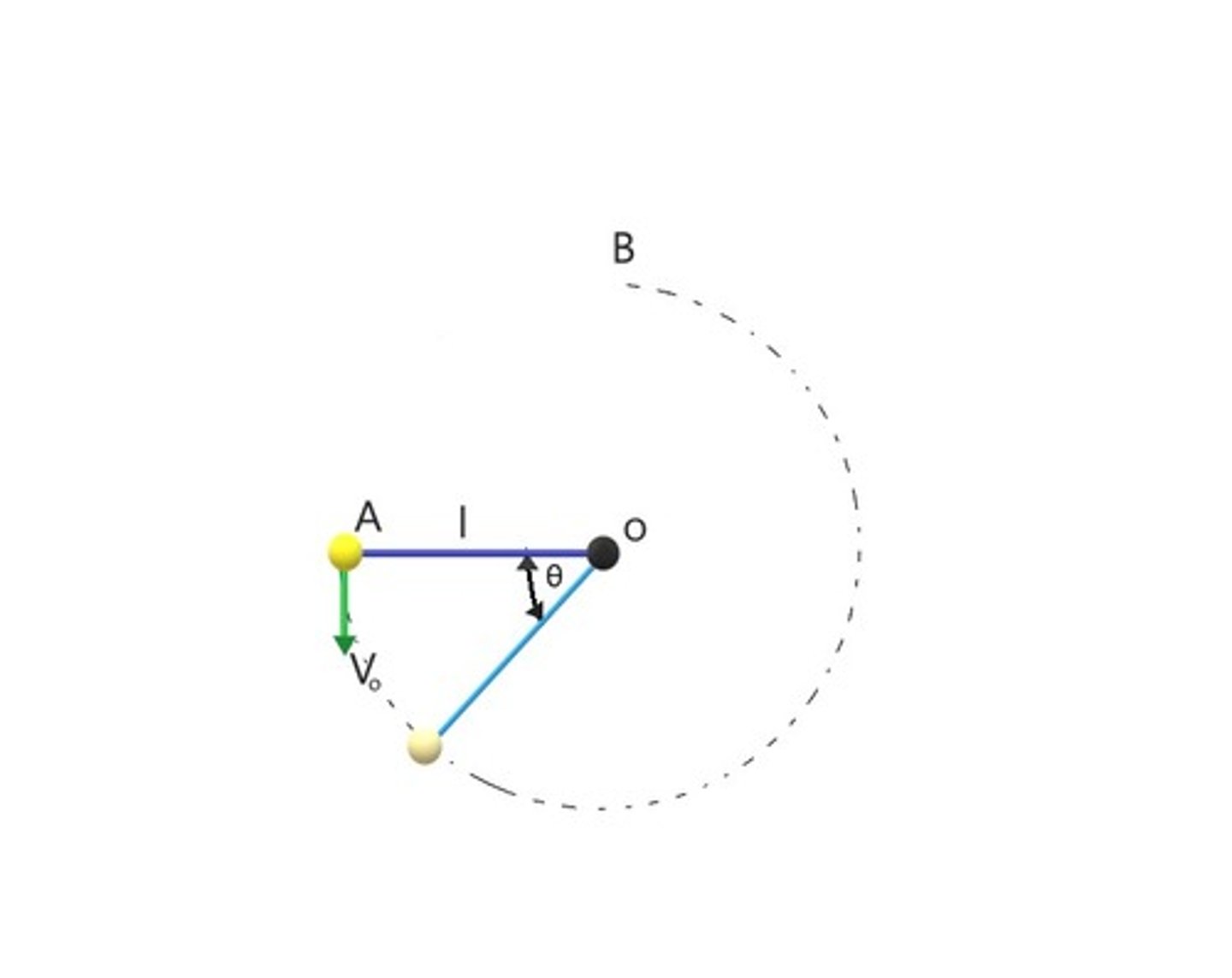
In this problem -- this time we use a solid rod instead of a cable. If the pendulum never makes it to Point B. Pick the right answer considering the following possible scenarios

a) Definitely the rod breaks between 6 o’clock and 3 o’clock positions

b) The ball will stop climbing when it has zero speed and falls back down

c) The ball will fall off the circular path when tension in rod is zero

d) Rod breaks between 9 o’clock position and 6 o’clock position

either b or d

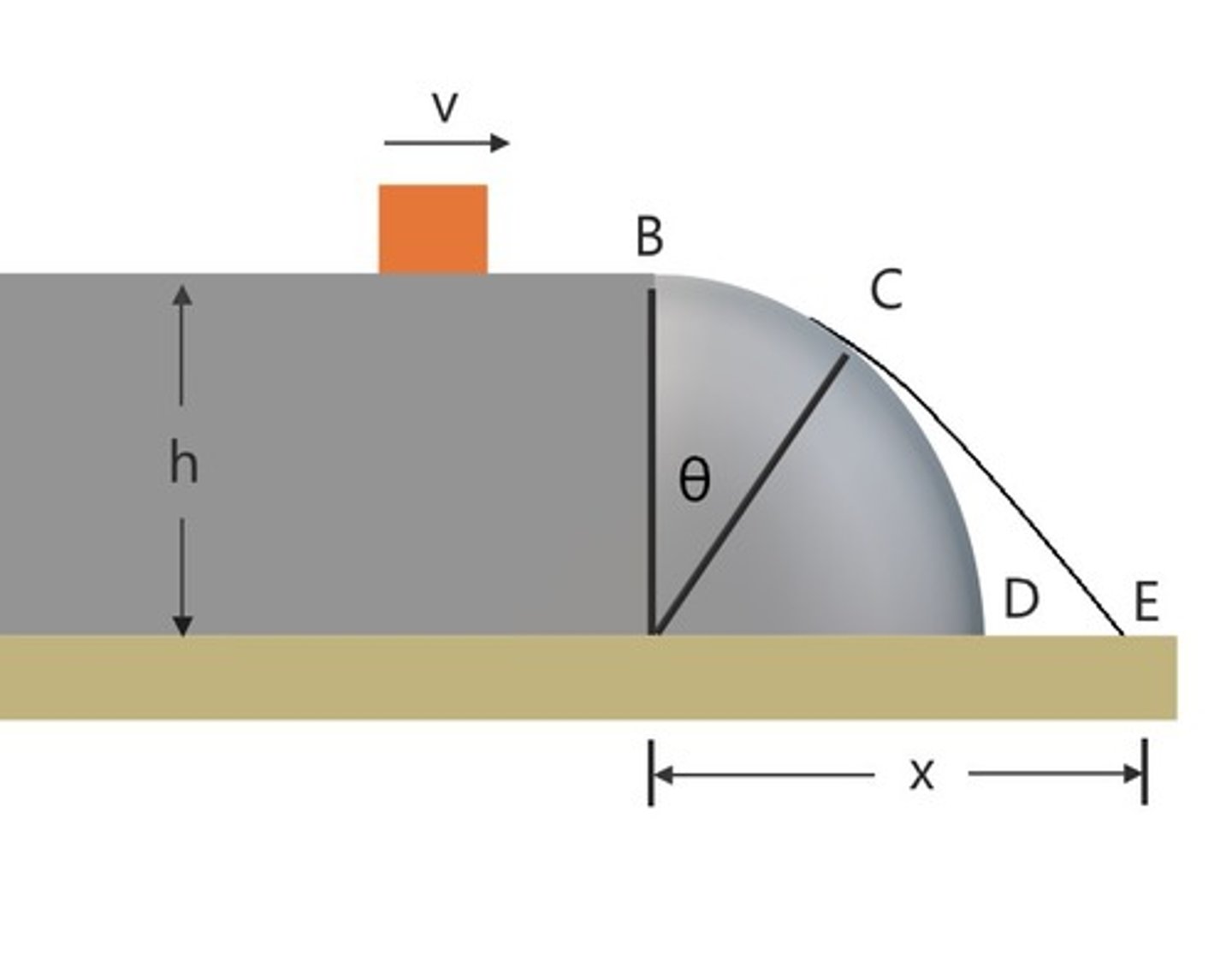
Can the package reach and touch point D?

No, it will never reach D.

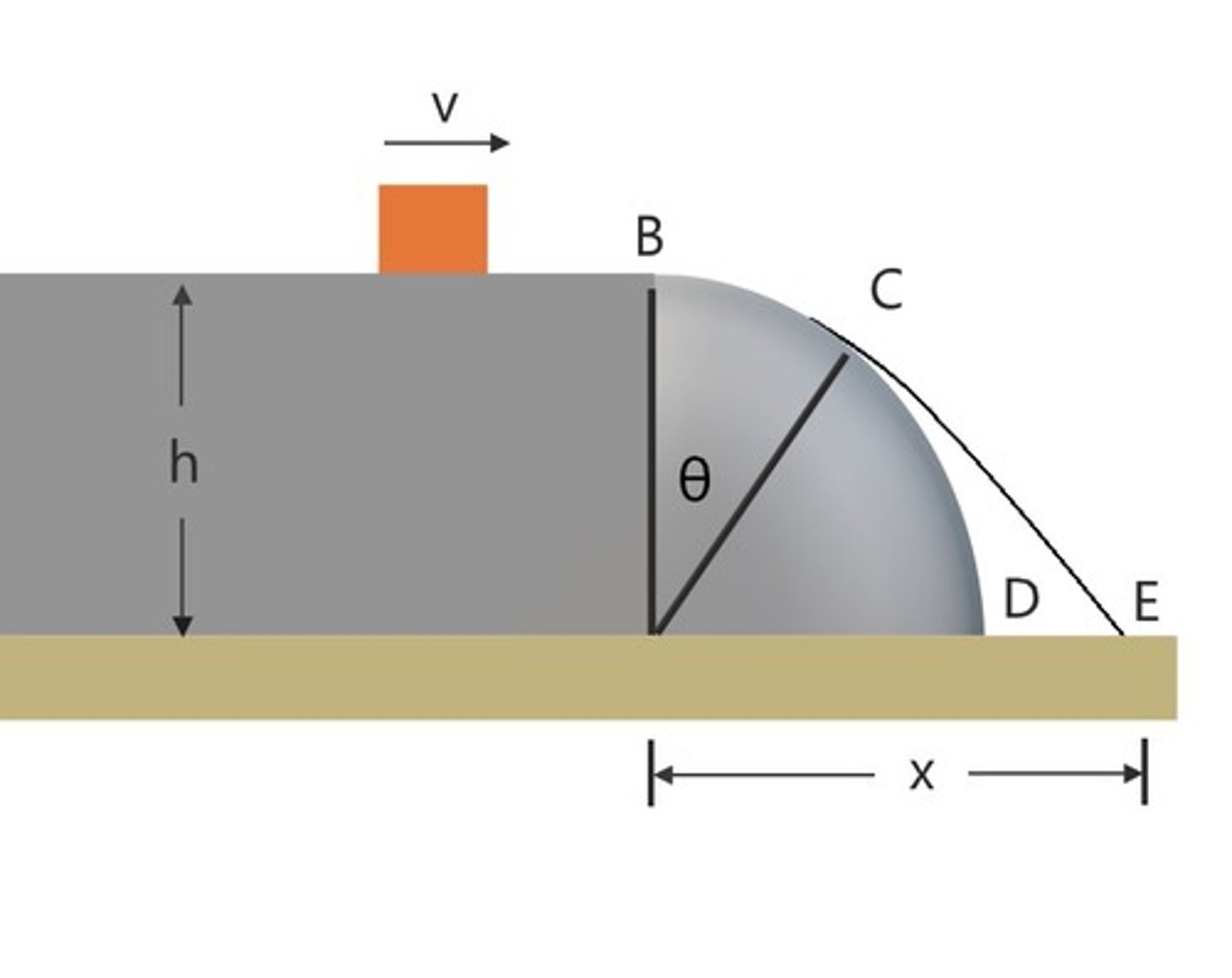
What happens if we increase the velocity v, which the box has at point B, by a huge amount?

The box might not enter the curved surface and will start a projectile motion to the right

In this problem, to make it to the position C, the _____ cannot become zero before reaching point B

Speed in right-hand side one and normal force in the left-hand side one

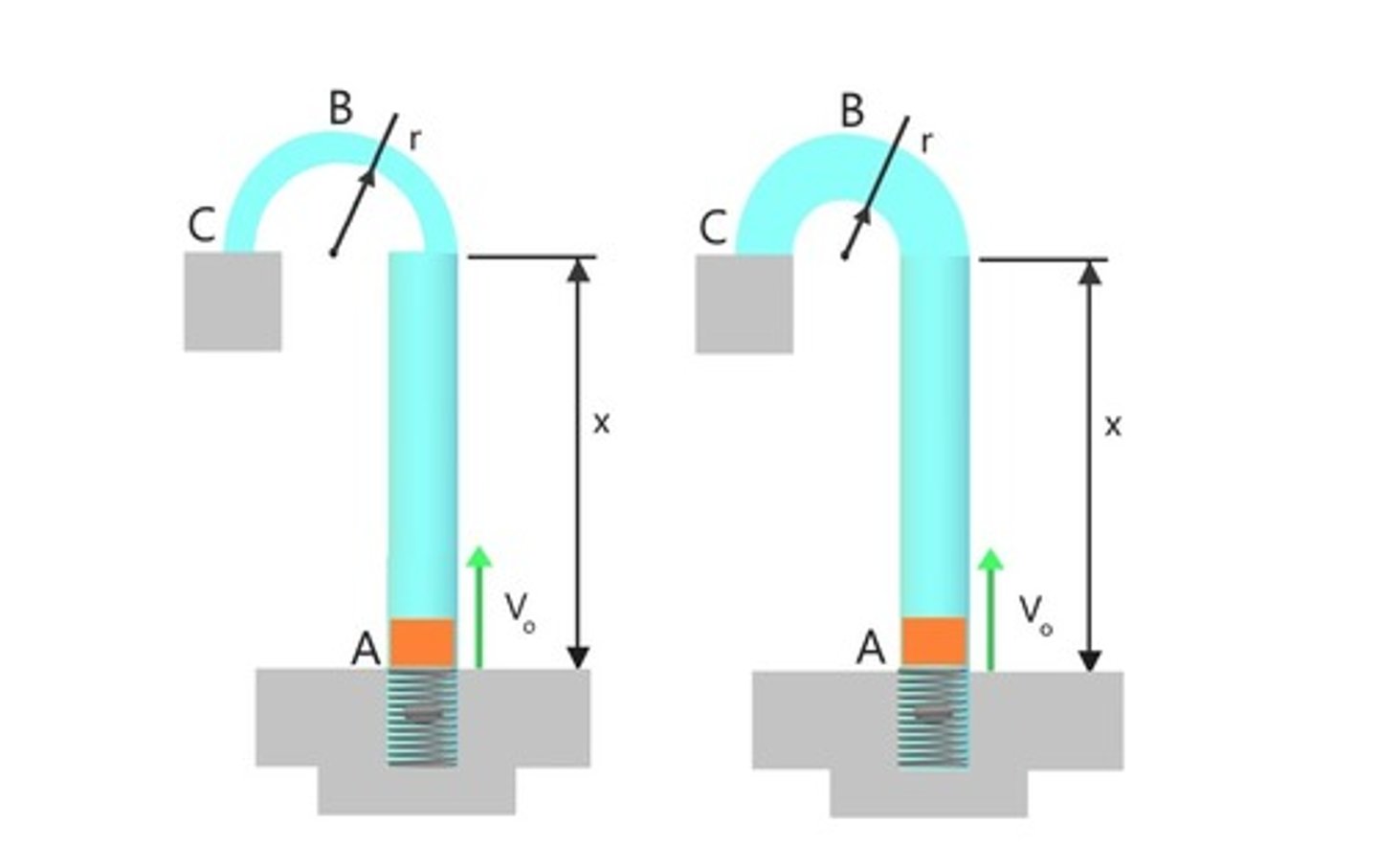
Suppose velocity of B is initially zero (i.e., B is at rest) and e= 1. What would happen next?

B moves away along the lines connecting the centers and A moves `down' perpendicular to that line

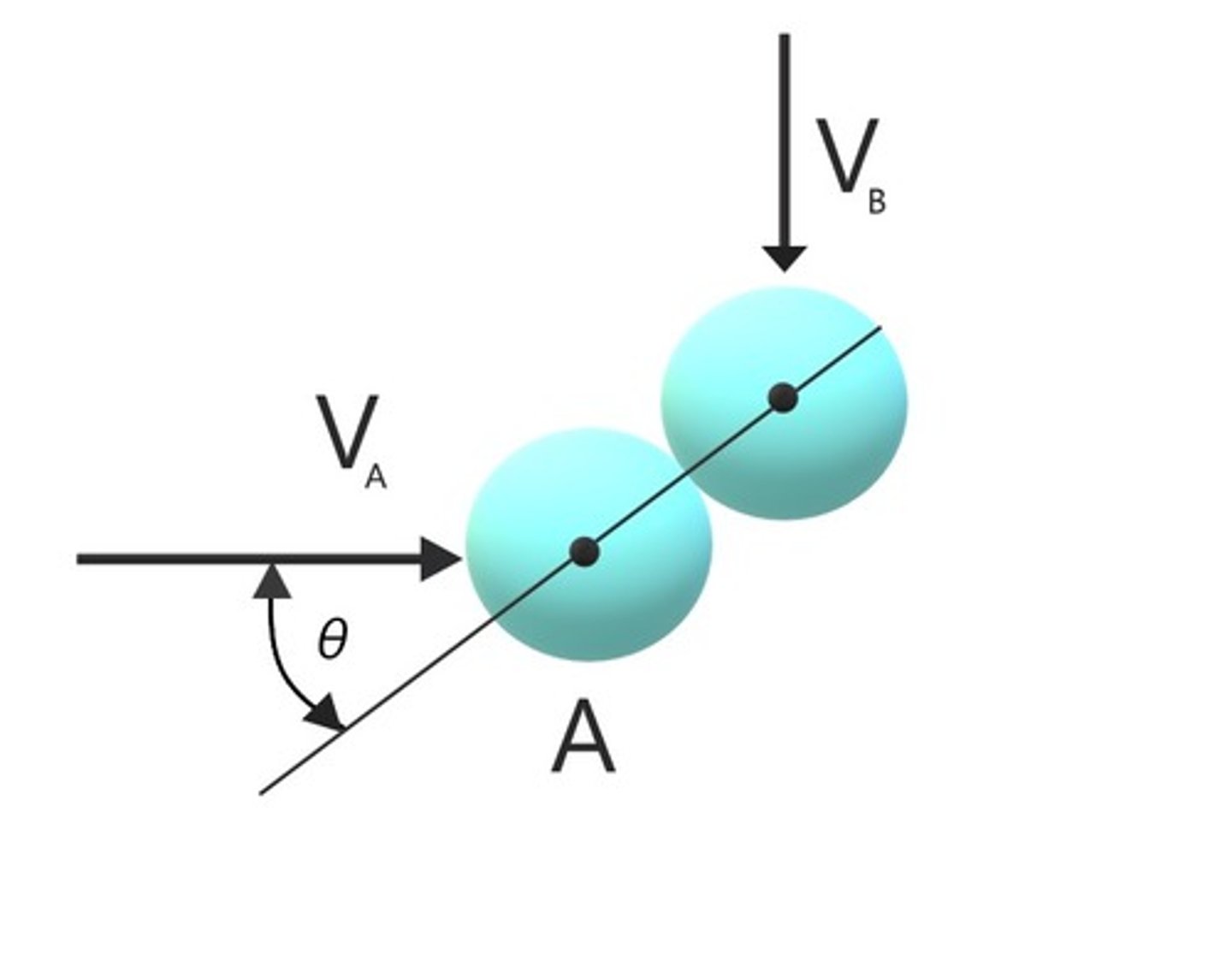
In what direction do impulsive forces act on the cart?

Normal to the slanted edge and normal to the ground

What happens to the Y- component of the impulsive force that the ball exerts in on the cart?

It gets countered (cancelled) by the impulsive force from the ground

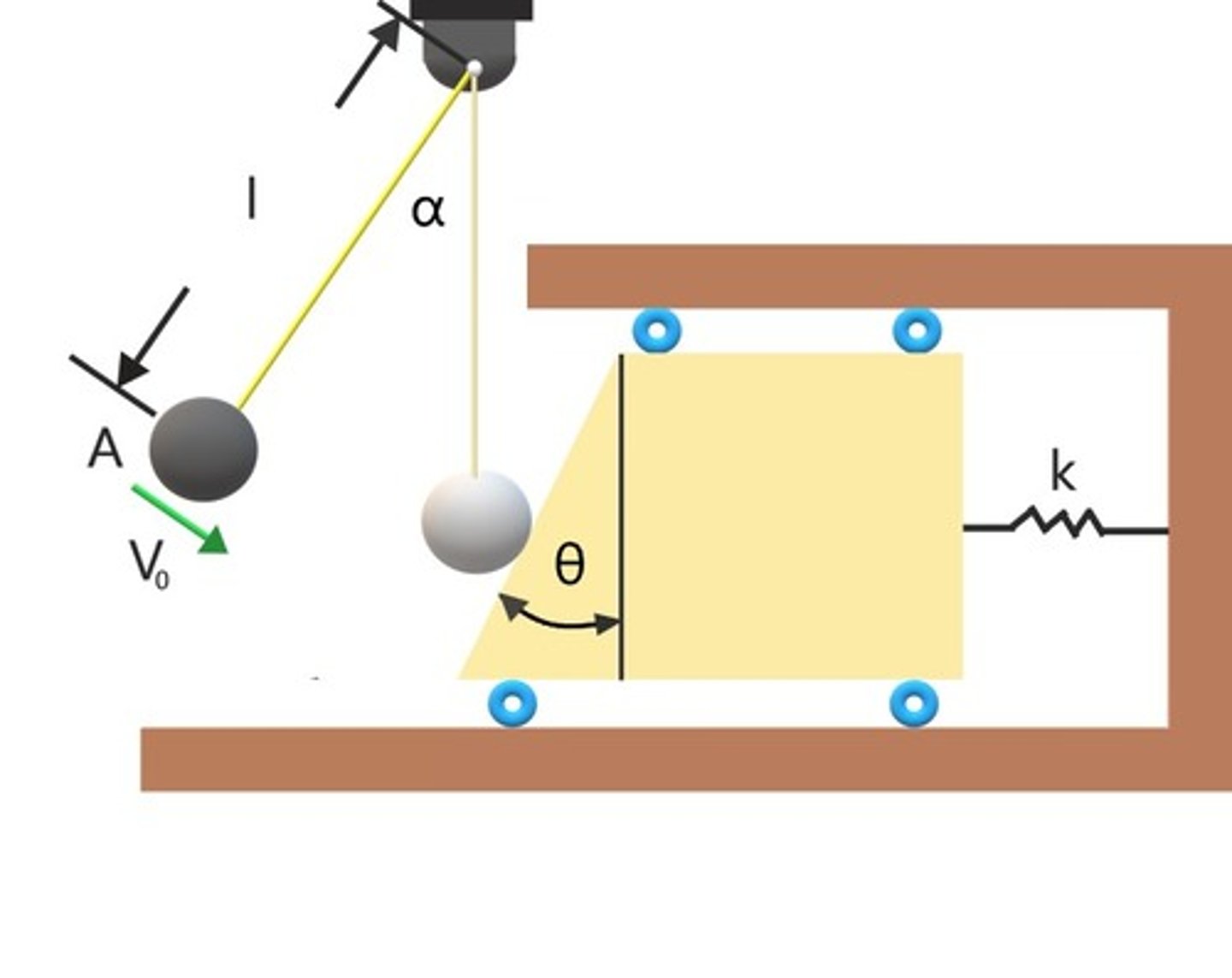
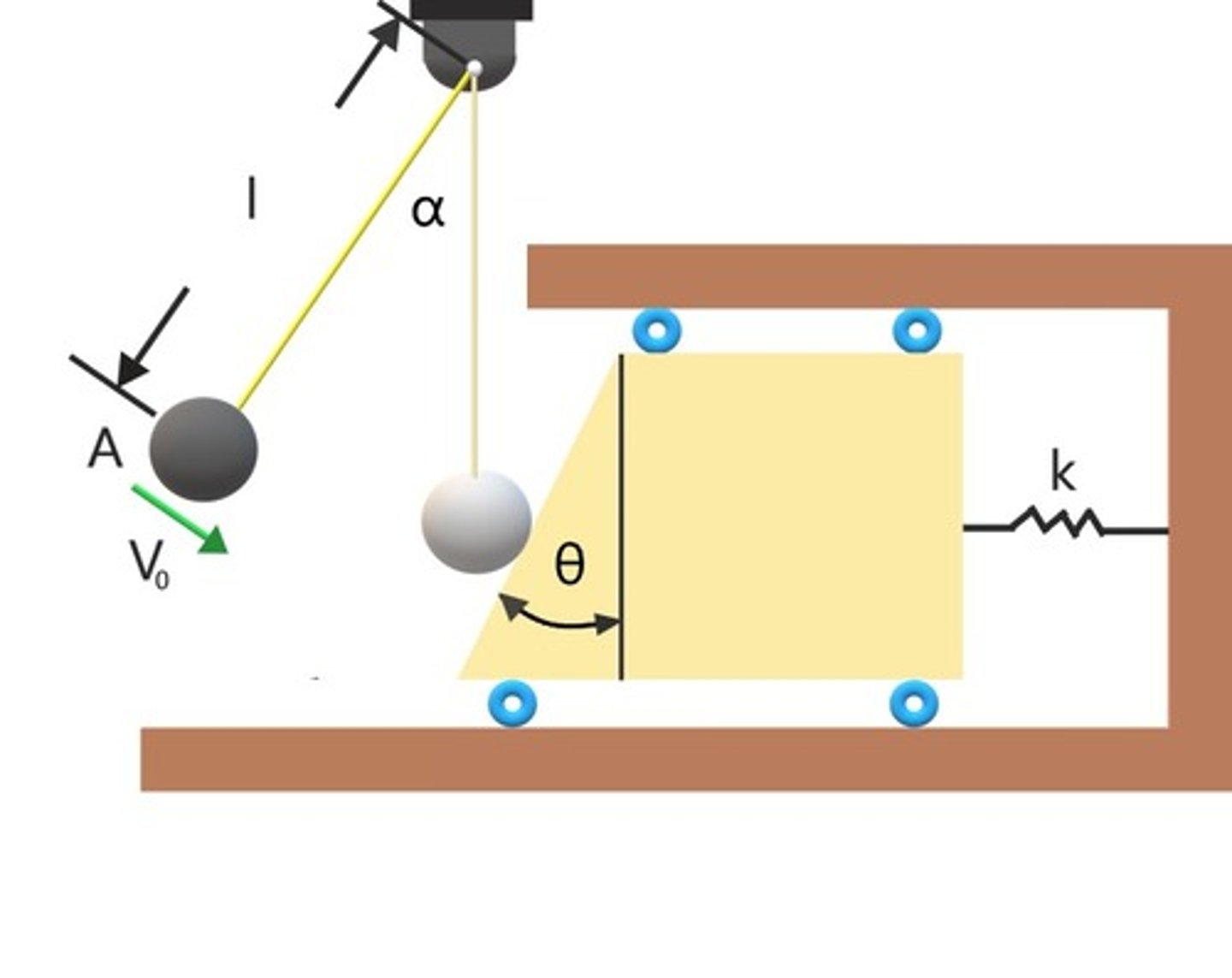
In the same problem, what can be said about the linear momenta of A +B in x and y direction, DURING the collision?

it is constant in x-dir and not constant in Y-dir

True or false: Linear momentum is conserved in each jump

True

For this problem, can we use conservation of linear momentum or conservation of energy?

Conservation of Linear momentum

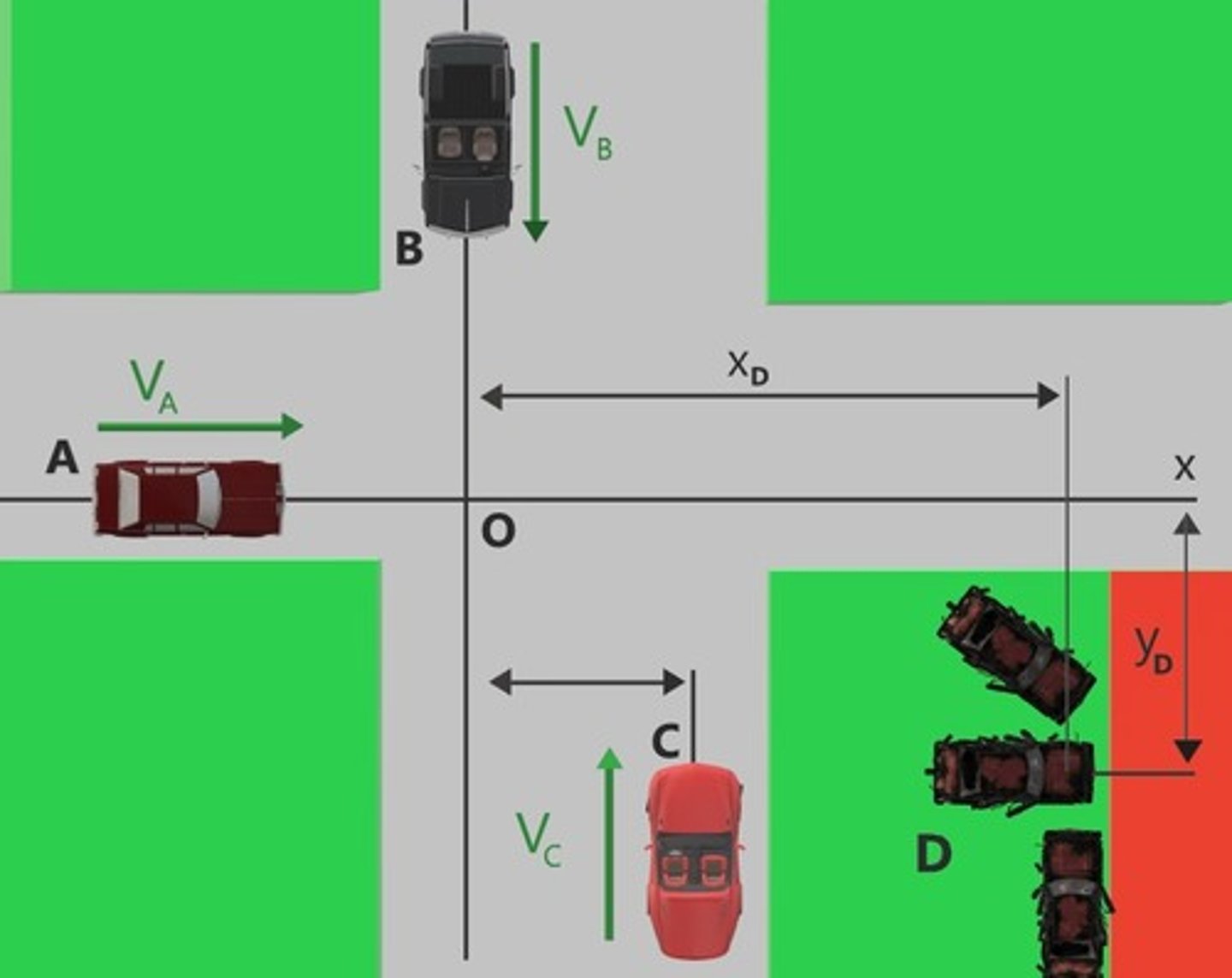
If velocity of something is constant, and you have two points that the thing goes through, can you guess the direction of the velocity?

Yes, since the direction is not changing while moving, we can find the direction with the two points.

What can be said about the normal force acting on A (from the support)?

It is less than total weight when B is sliding down

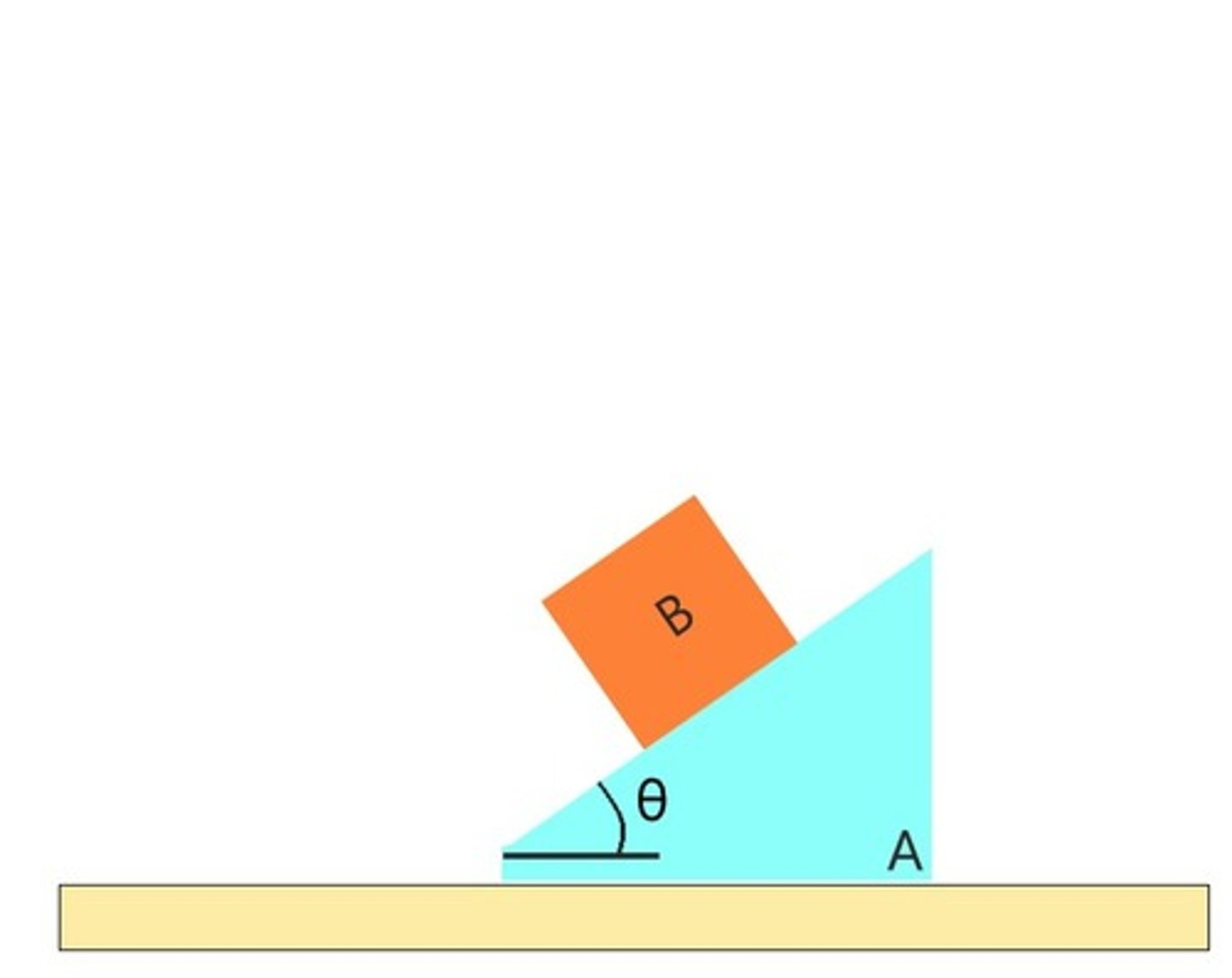
What can be said about momentum and energy in the previous problem

energy is conserved and linear momentum is conserved in X direction

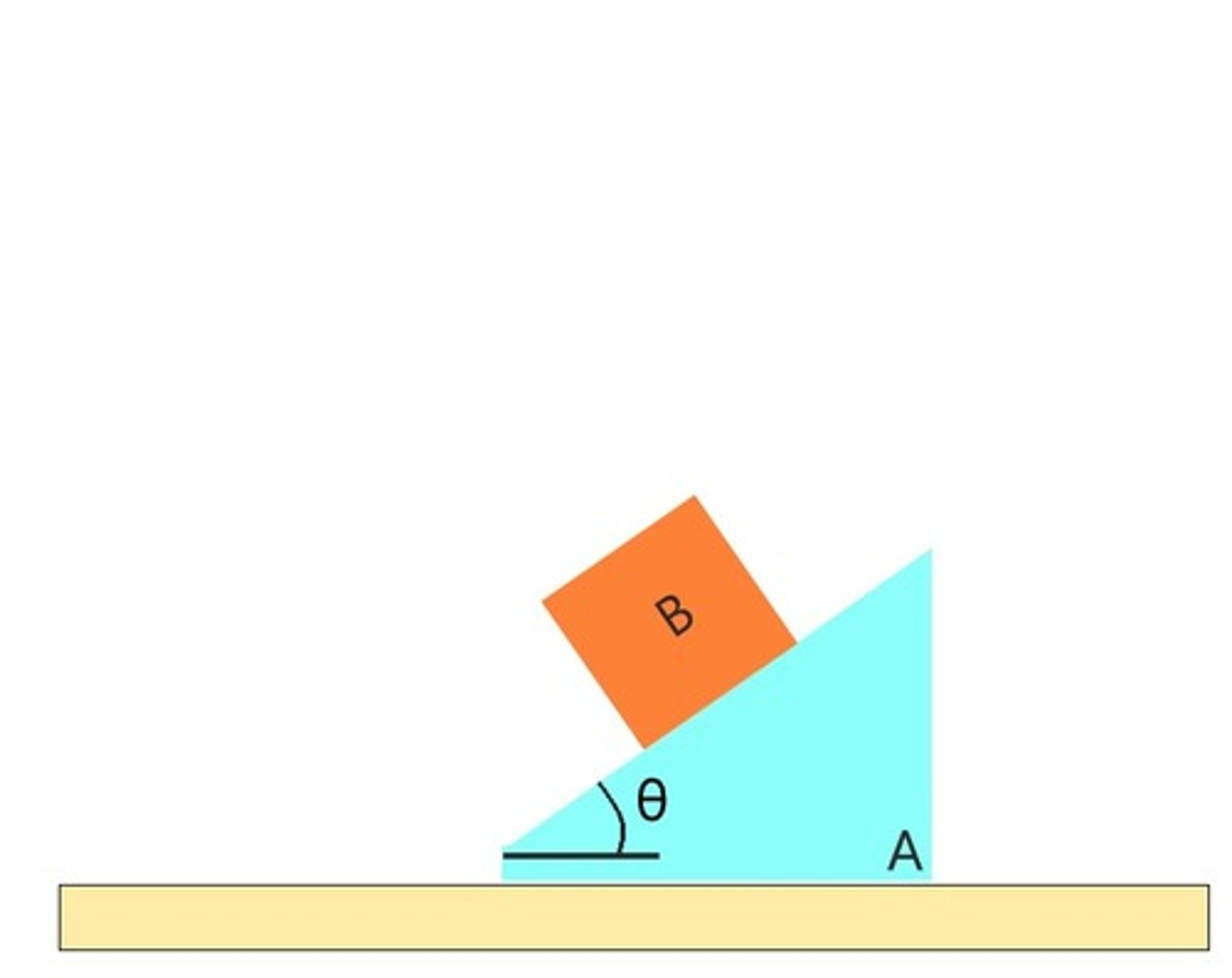
In the problem where block B slides down block A. Suppose there is friction between A and B -- not no friction between A and the ground. Pick the correct statement

Linear momentum is conserved in x-direction

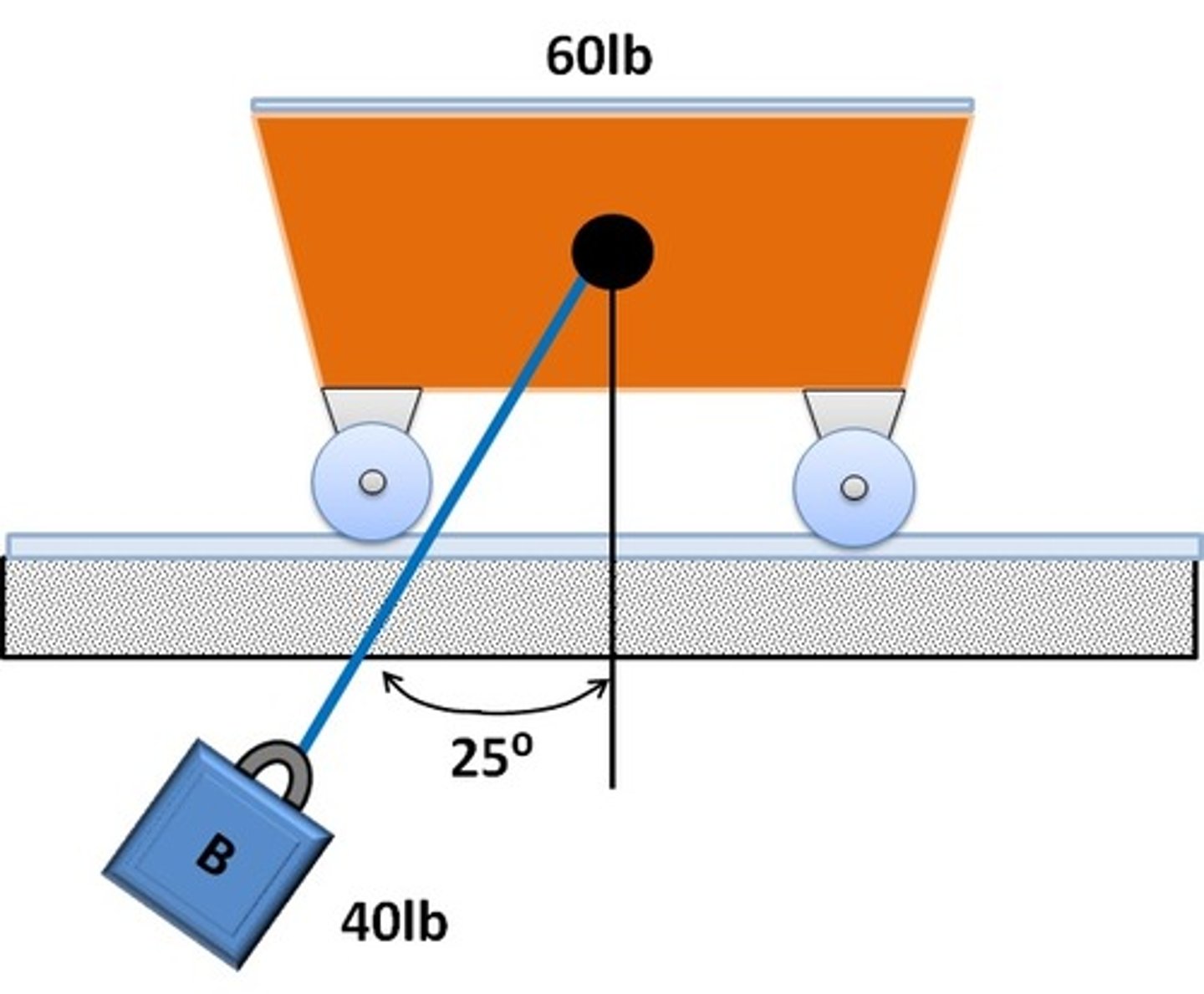
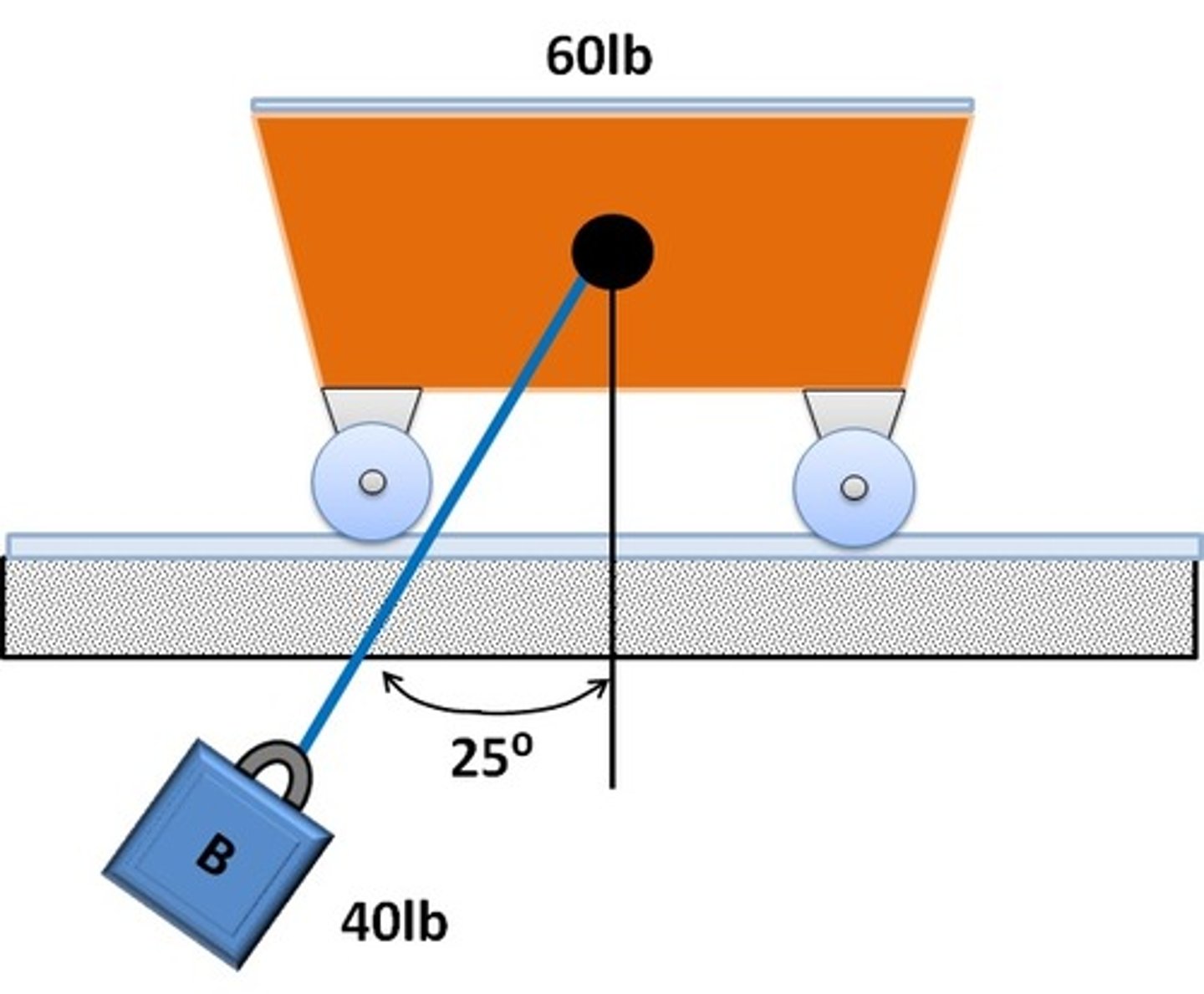
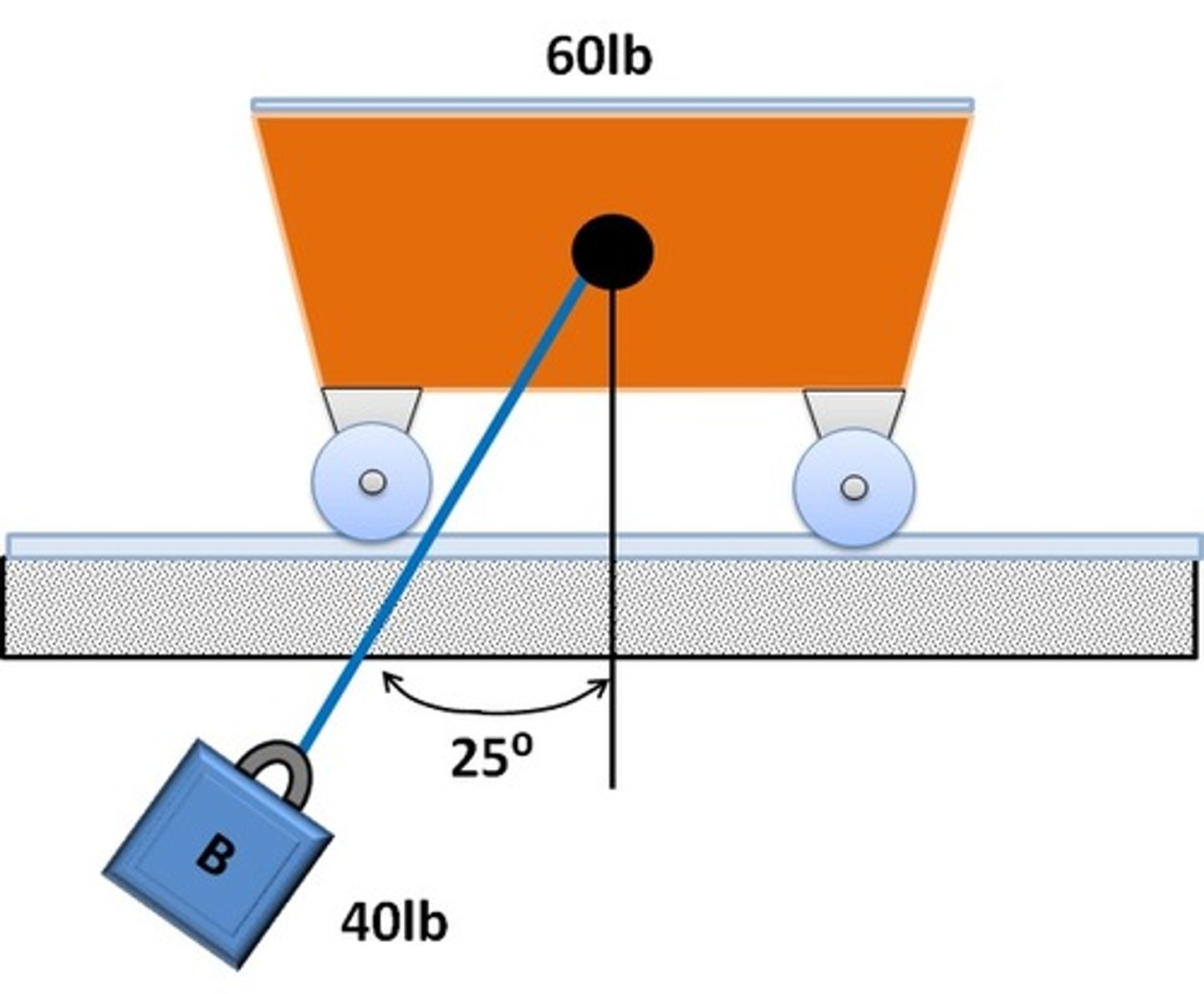
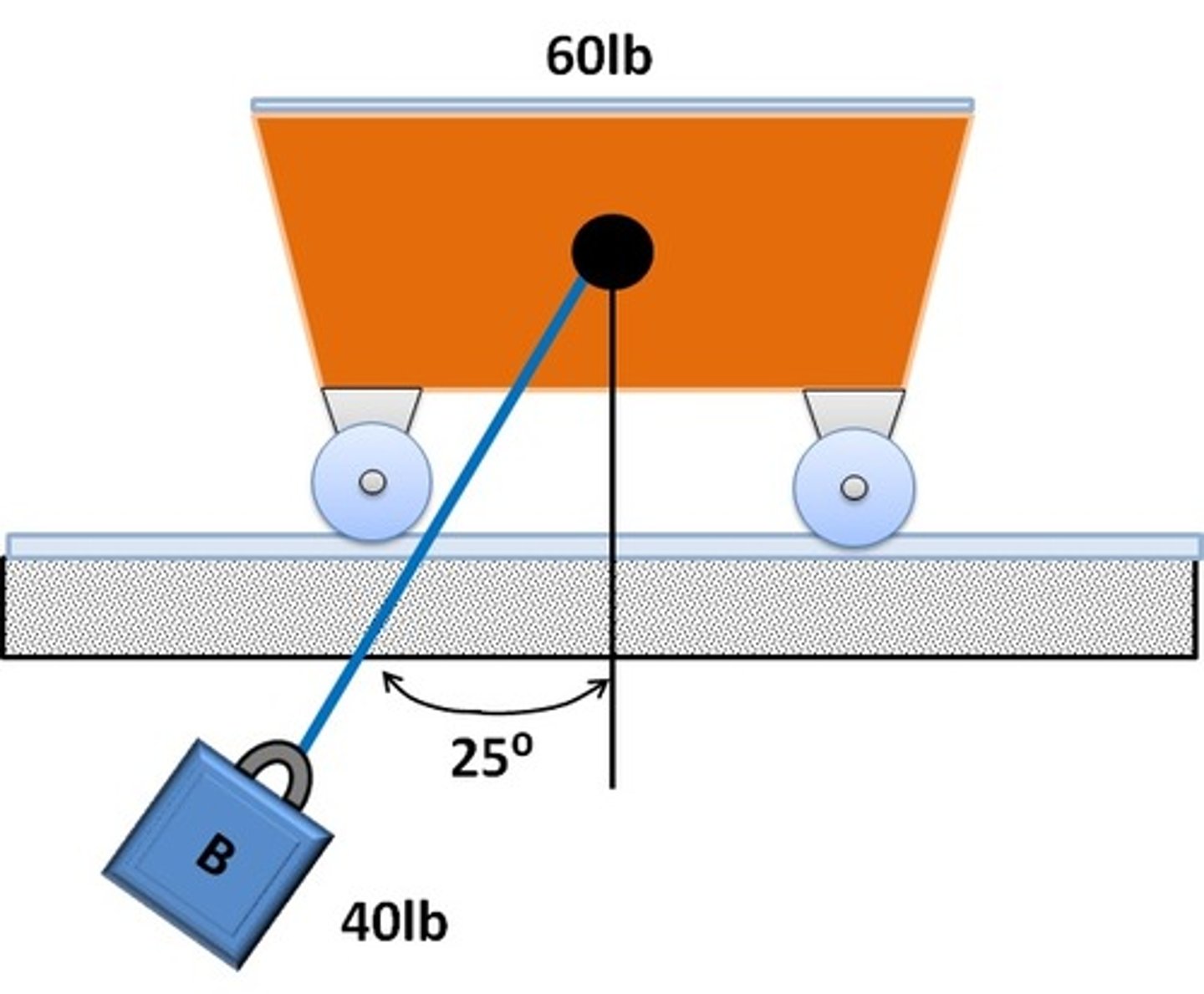
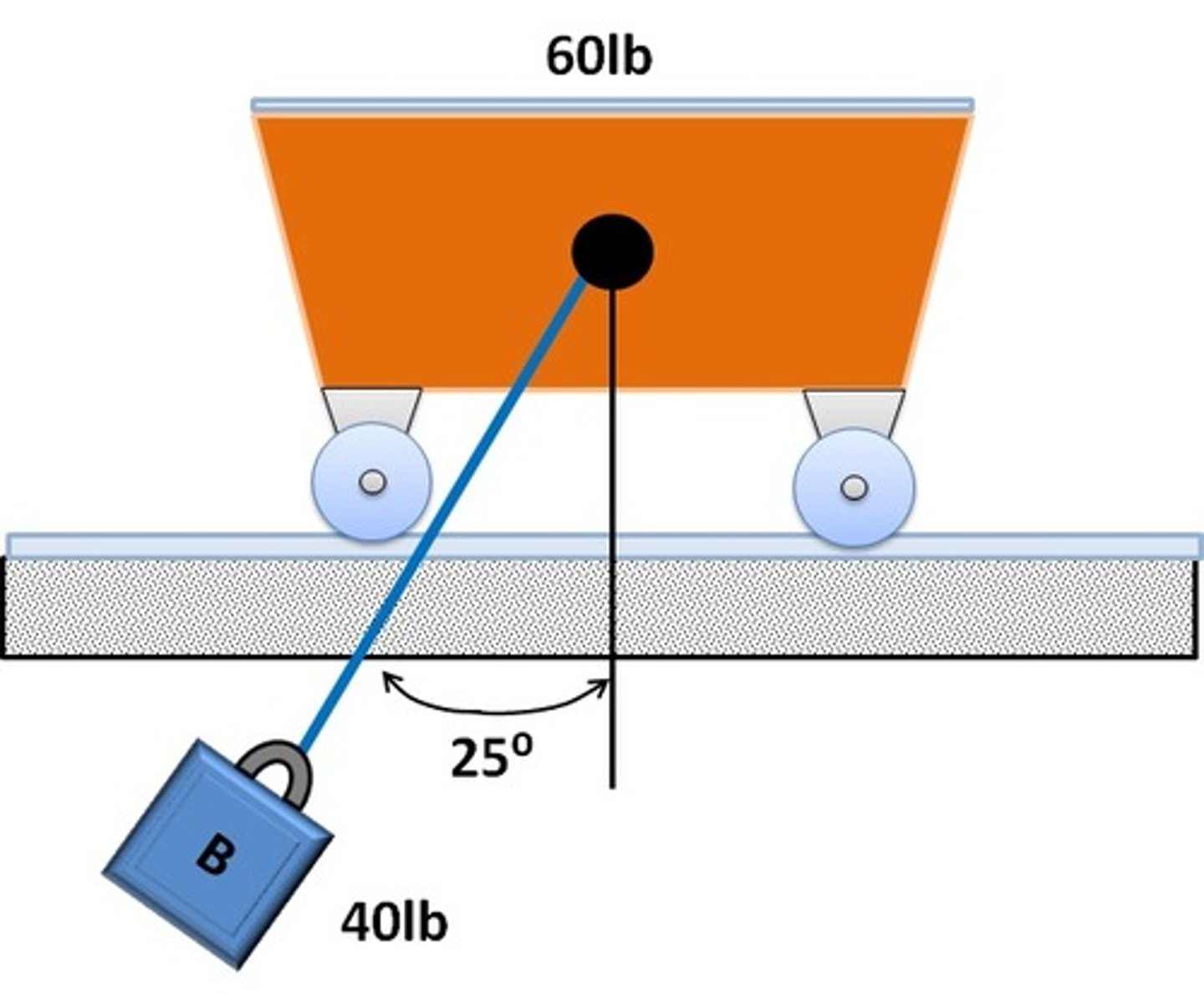
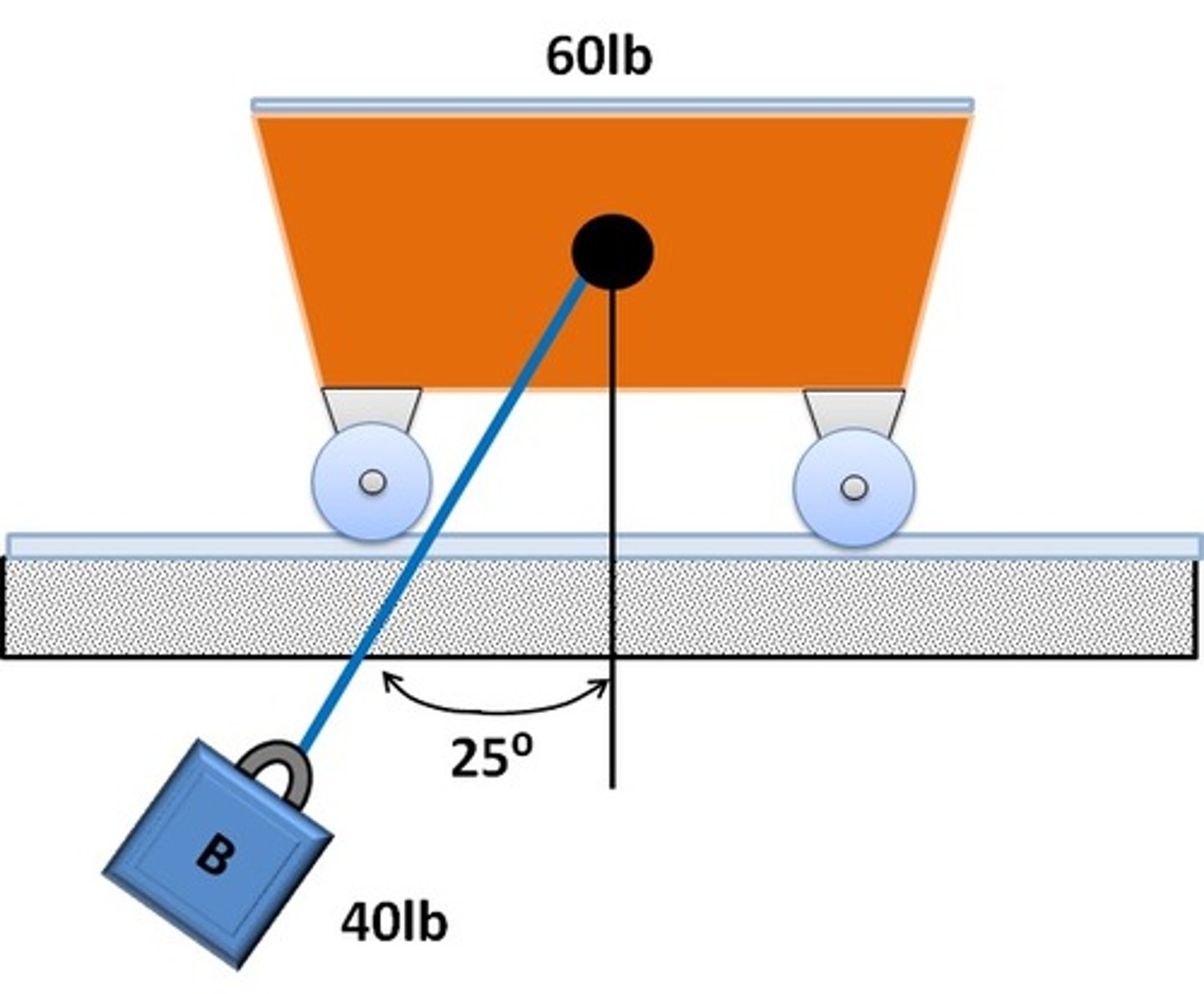
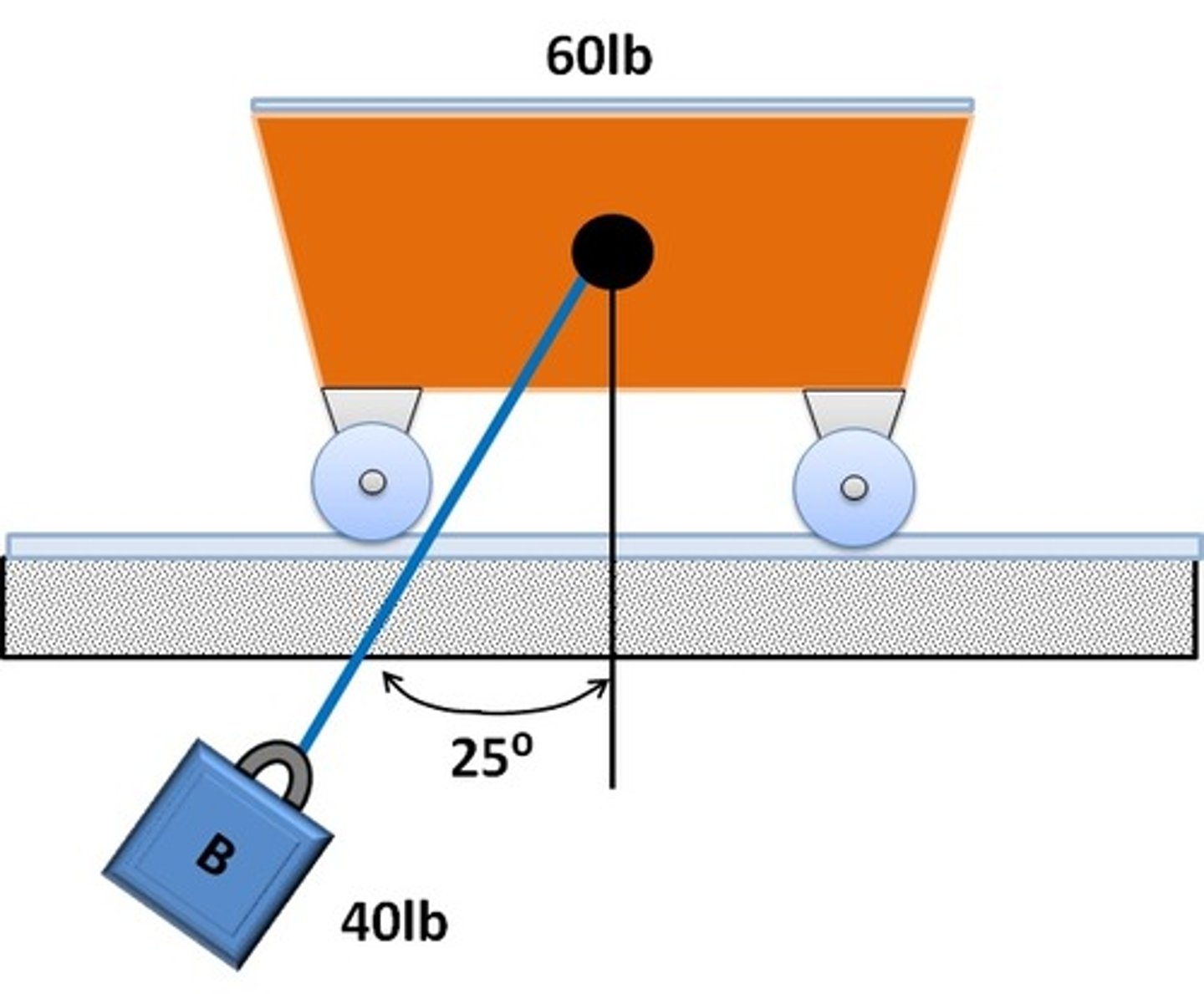
In the problem where B is released with zero velocity at some angle (say 25 degrees). When will the velocity of the cart and block equal to each other?

At max angle.

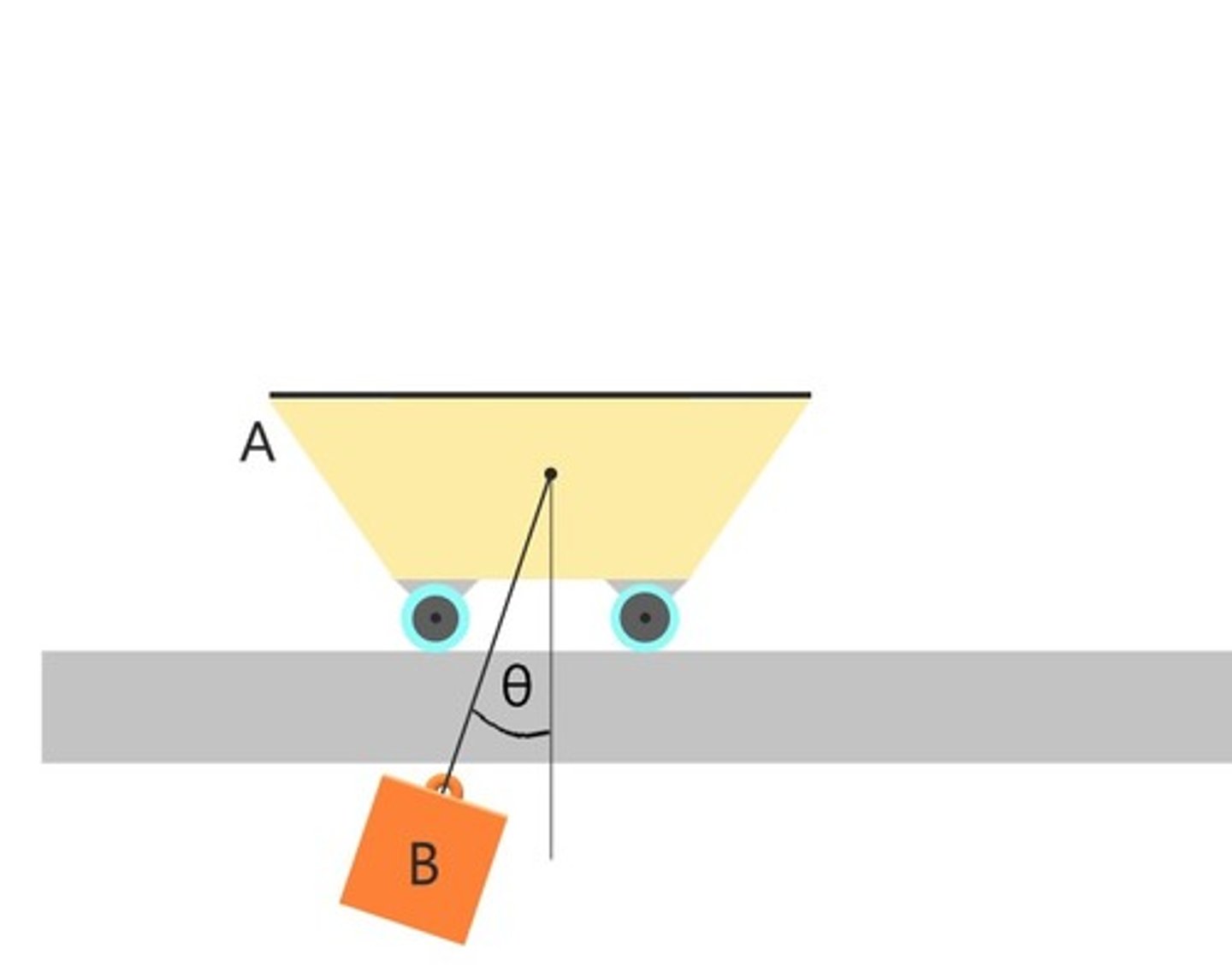
What can be said about the work done by the tension in the cable?

It is equal and opposite on the cart and the weight (so net work of zero)

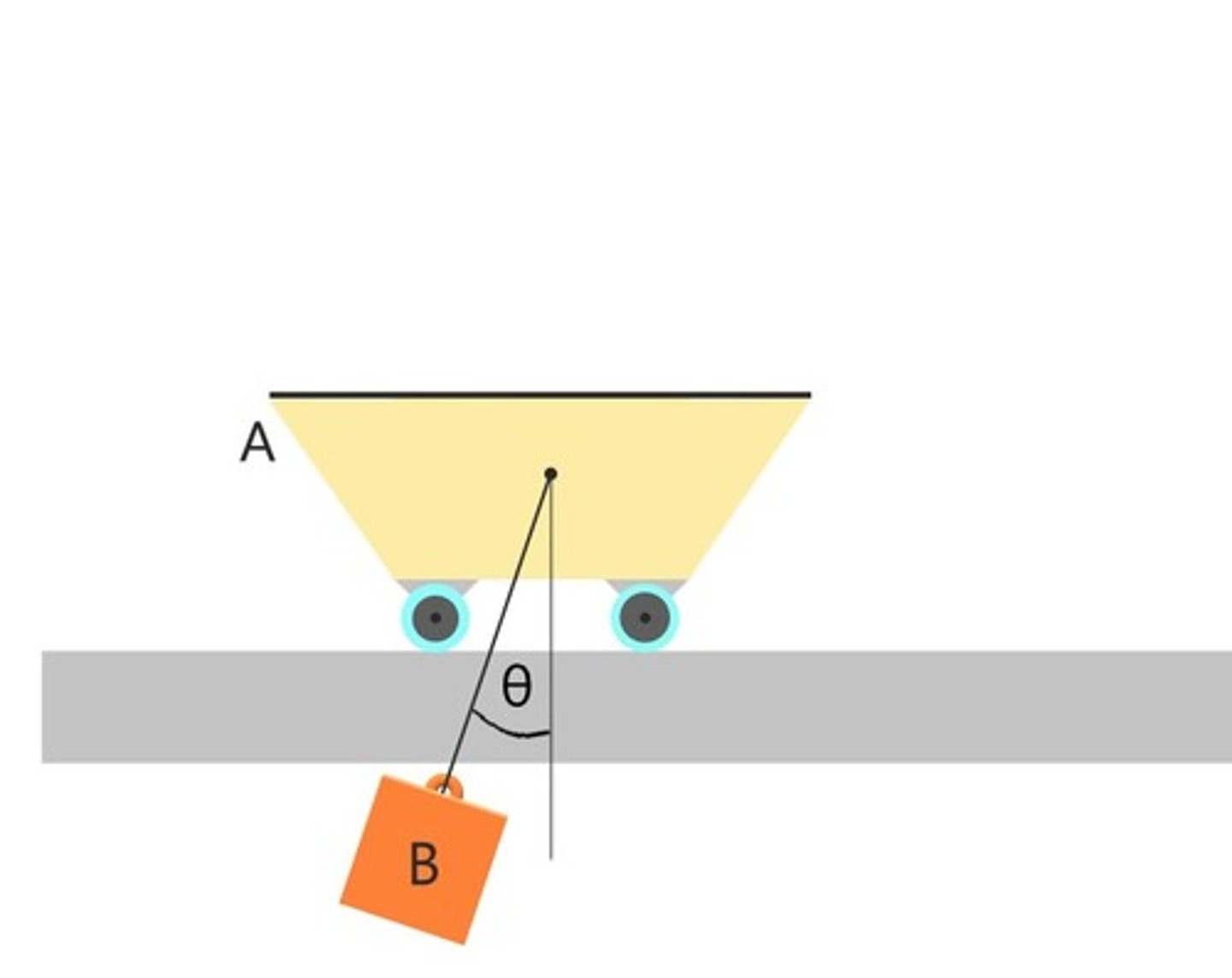
True or false: Linear momentum is conserved in x direction and energy is conserved

True

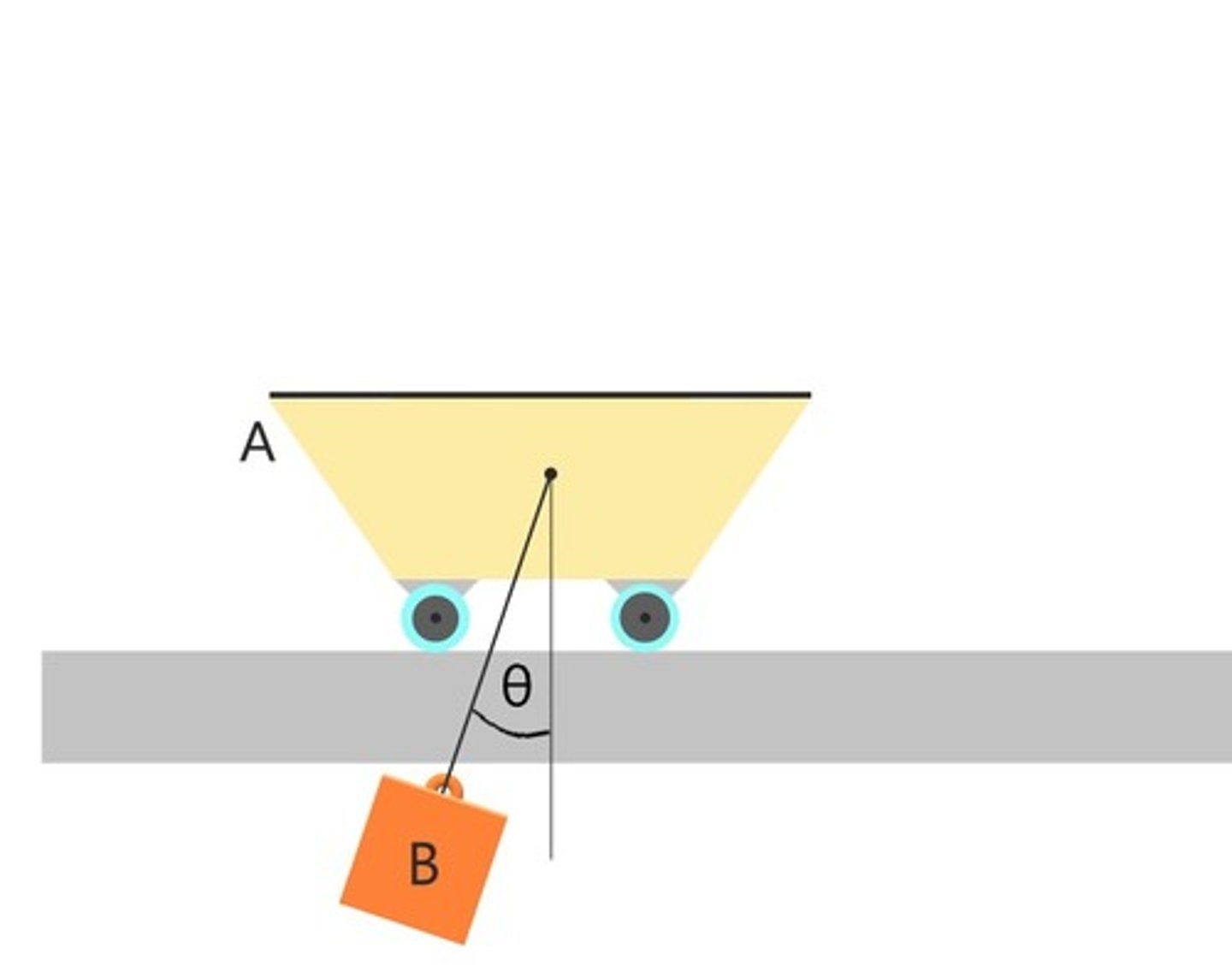
In the multi-ball collision problem (assume e is NOT 1). In the case that A hit one first and then the other one:

Solve 2 oblique collision problems: A hitting one first, changes velocity and then hits the other - also oblique

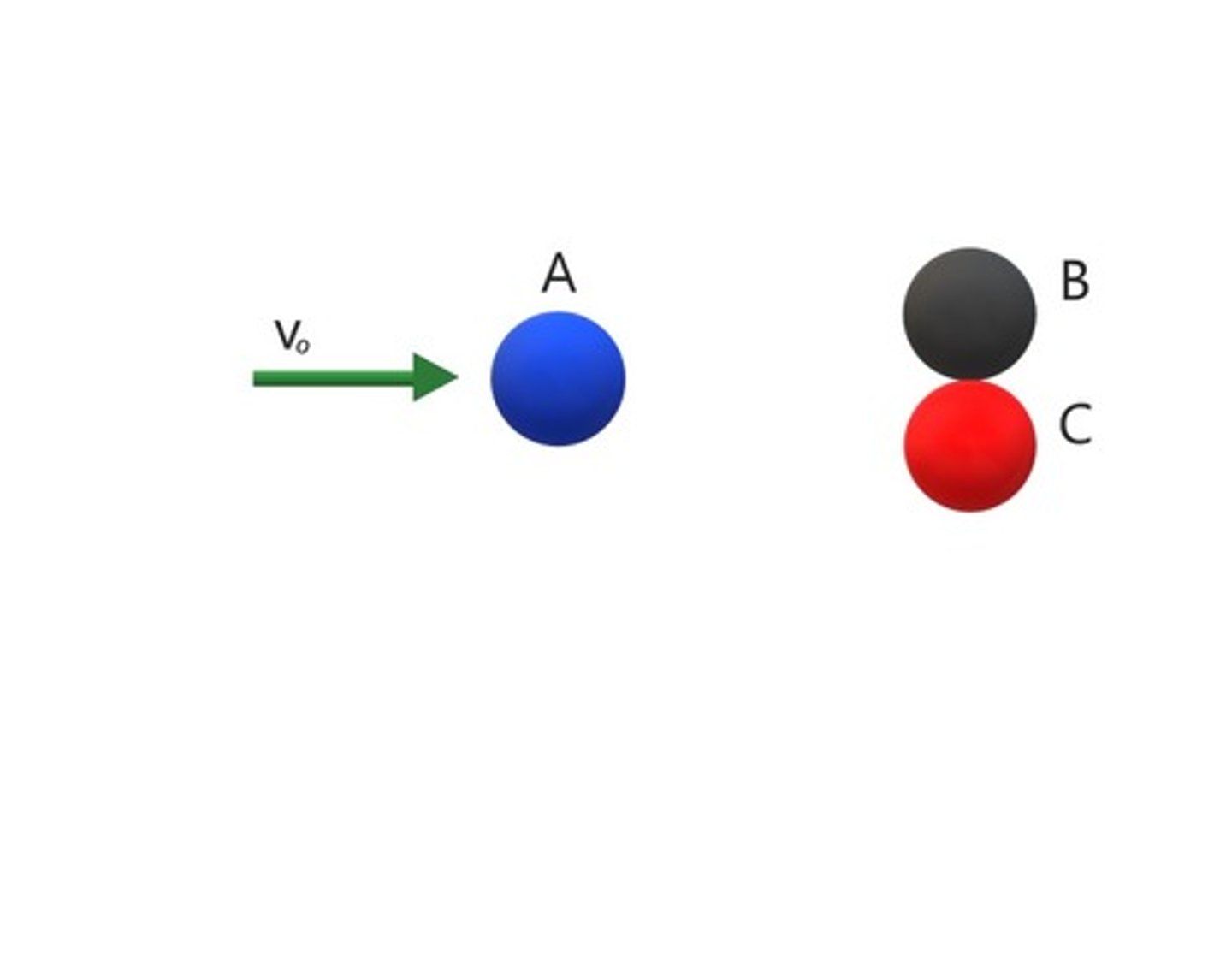
True or false: Spring does equal and opposite work on A and B (so net zero work done on A and B)

True

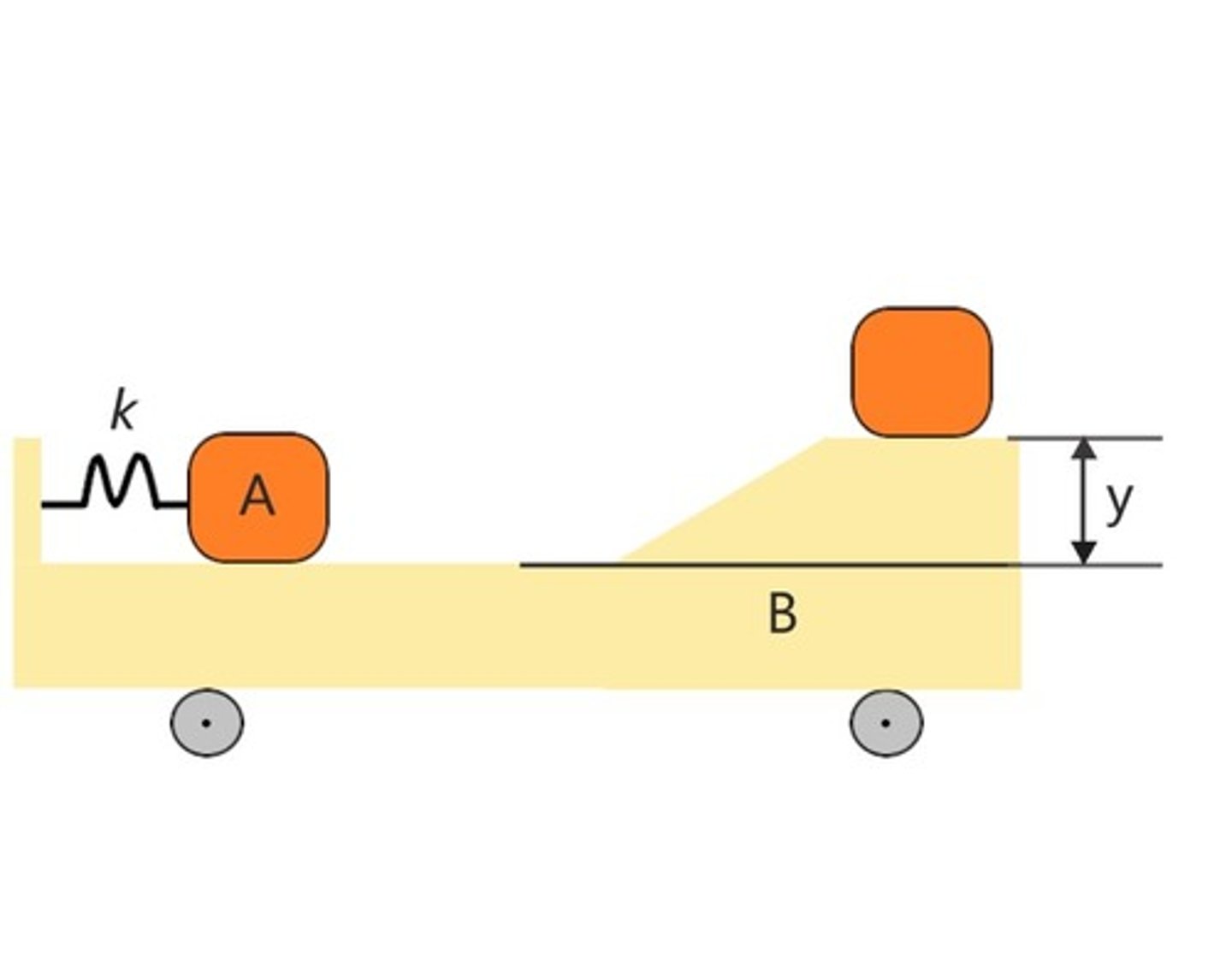
In the previous problem, is linear momentum conserved (for the system) in any direction?

Yes, only in x-direction.

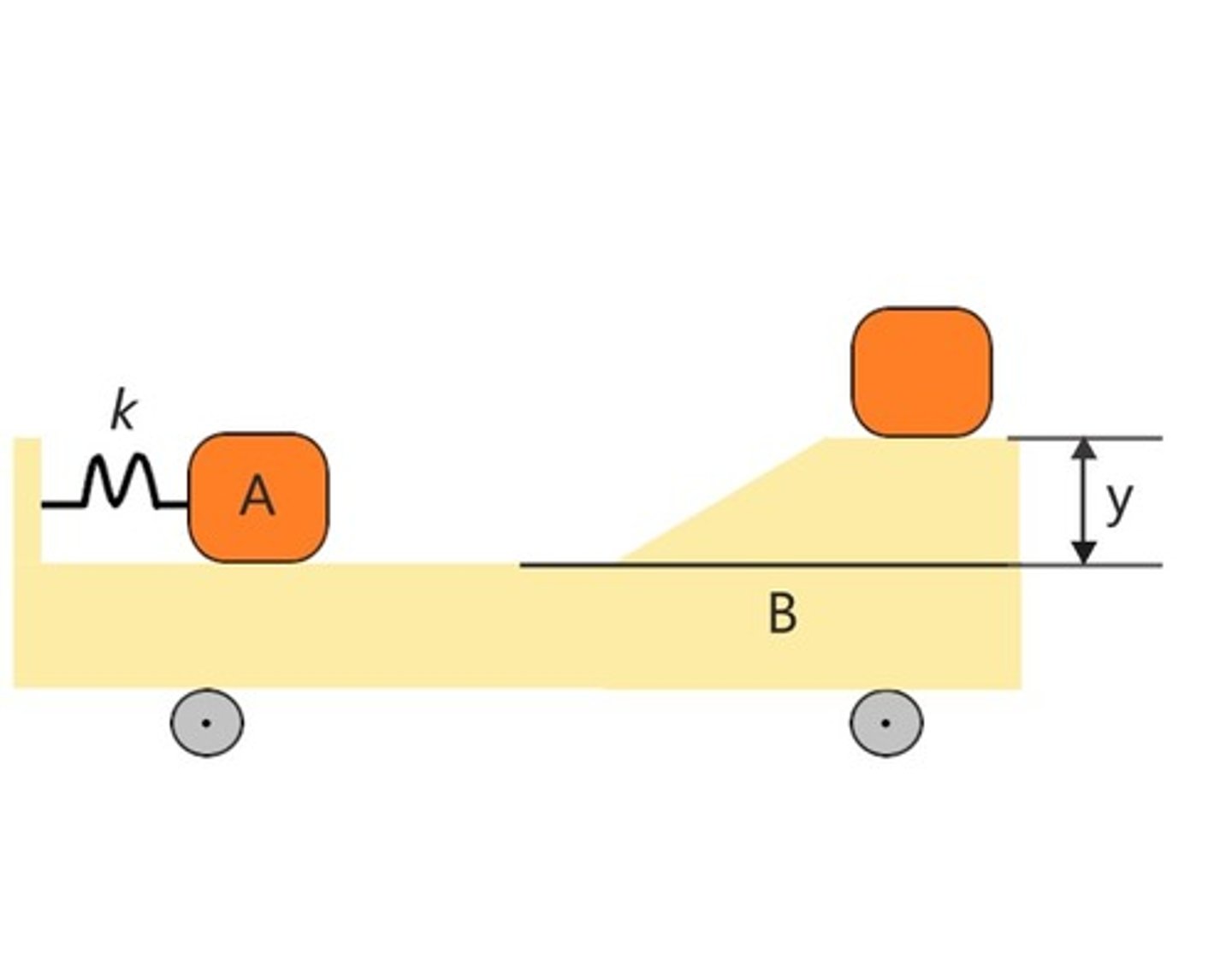
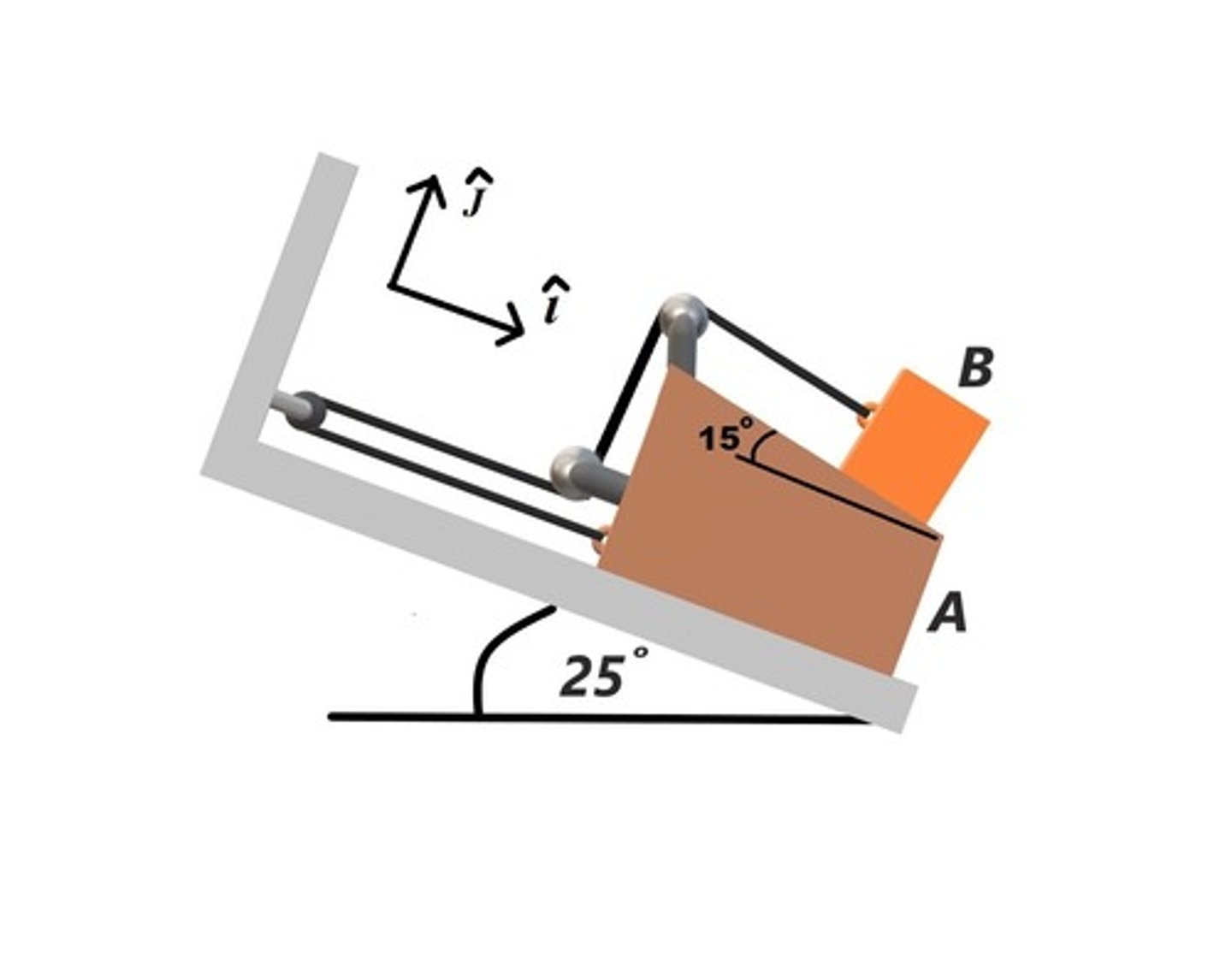
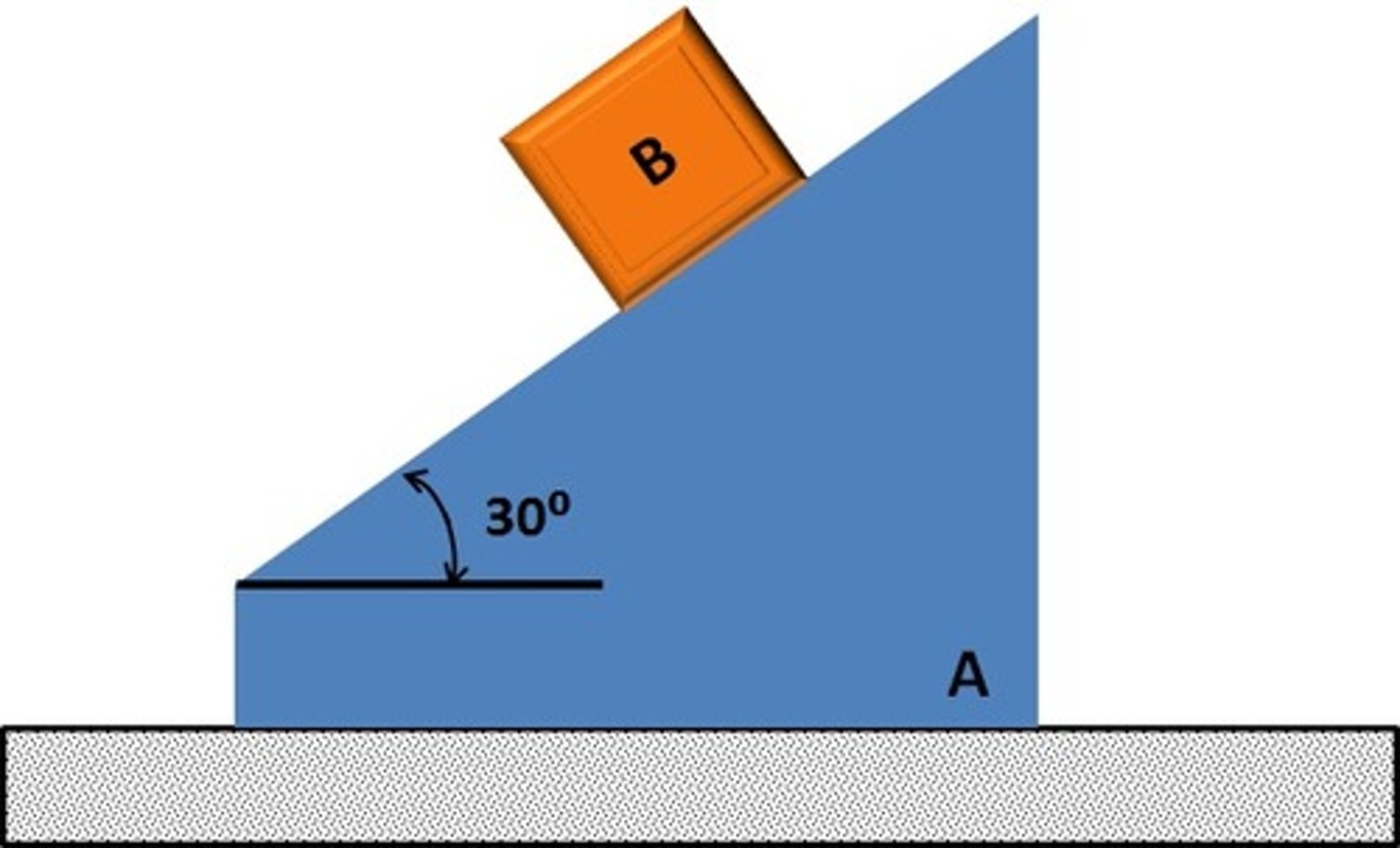
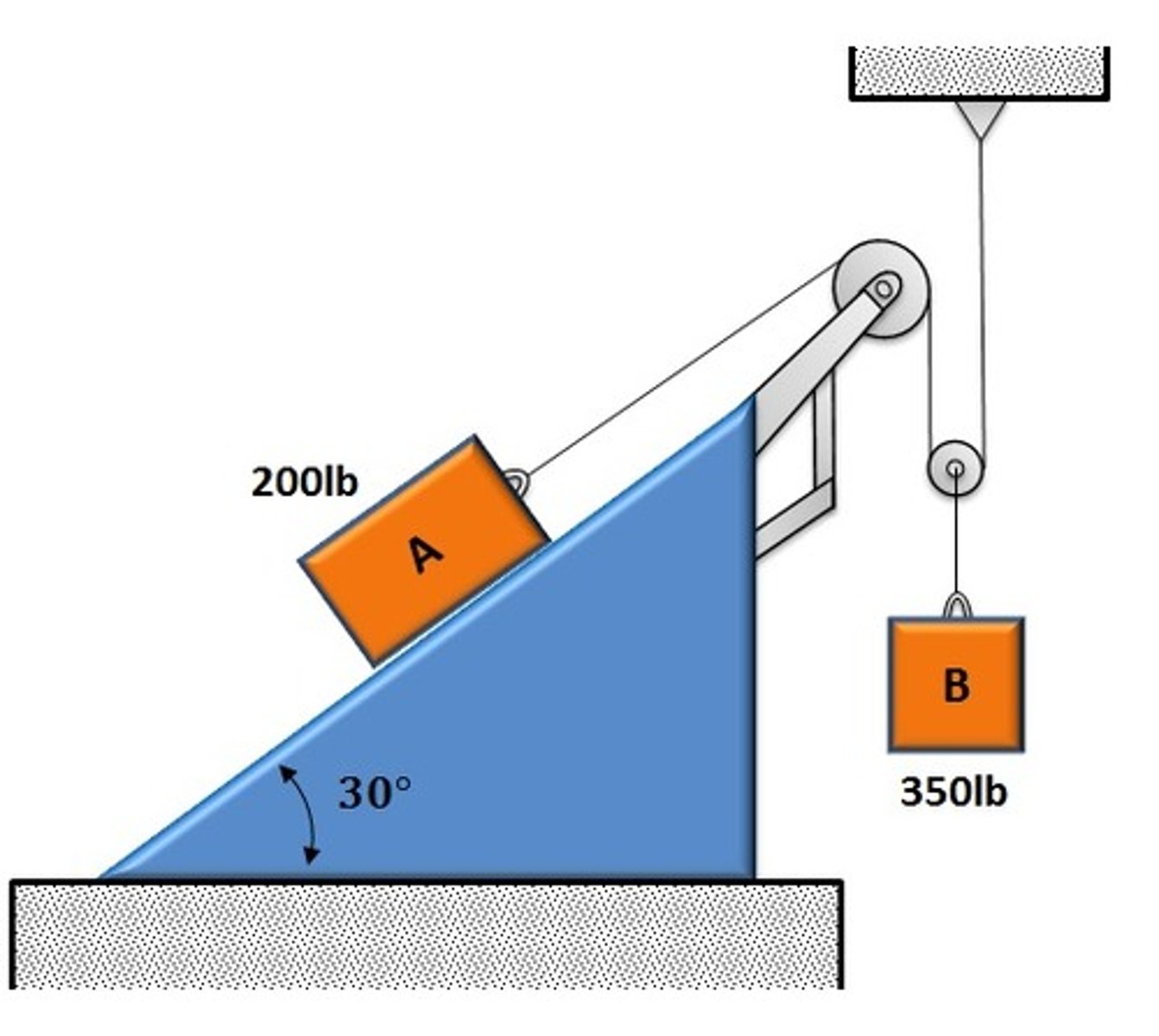
In the figure shown, ignore all frictions and masses of the pulleys and the cable. The incline is fixed and not moving.

What is the equation of motion for mass B:

m_B a_B = m_B g -2 T

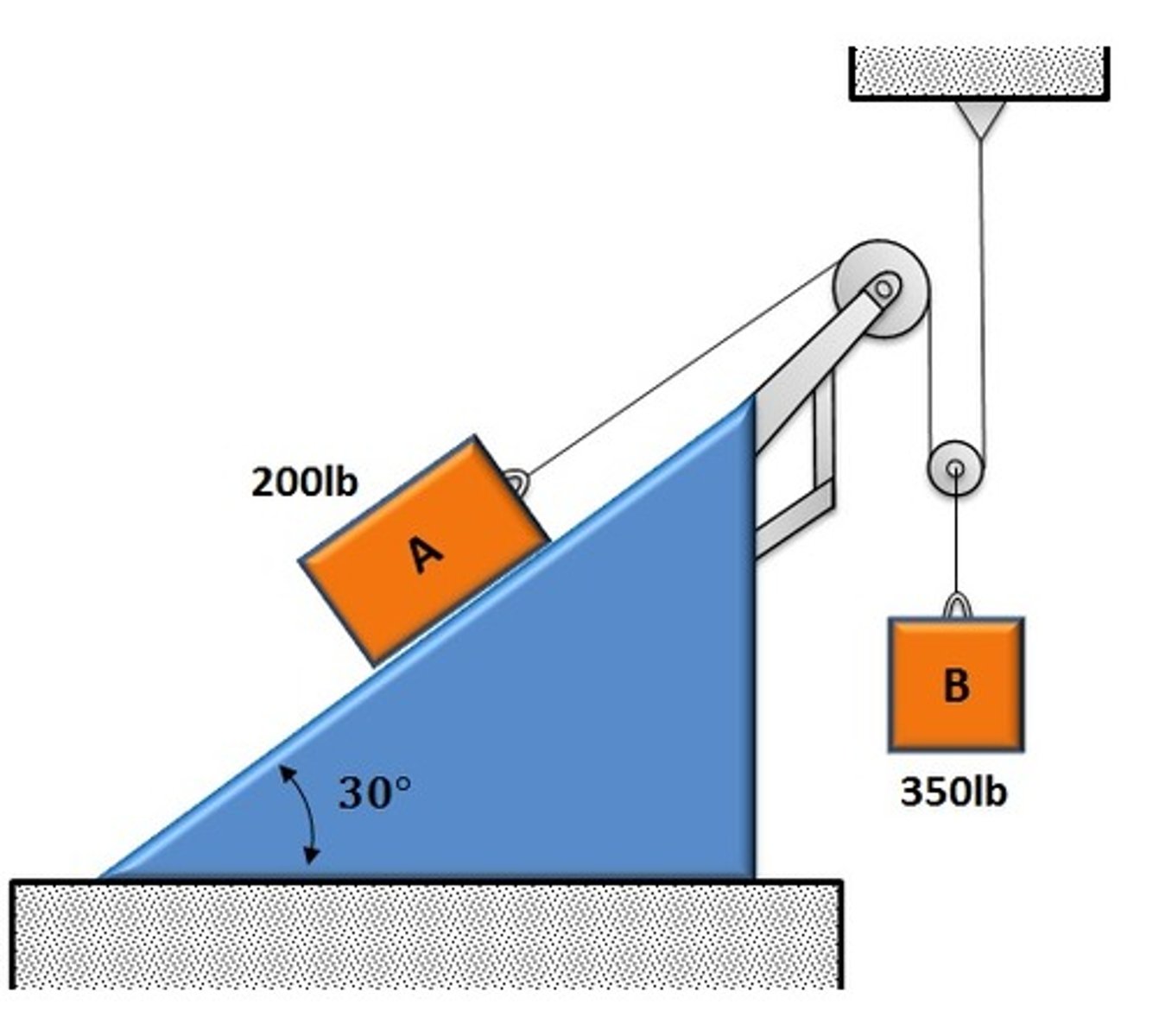
What is the equation of motion for mass A?

m_A a_A = T-m_A g sin 30

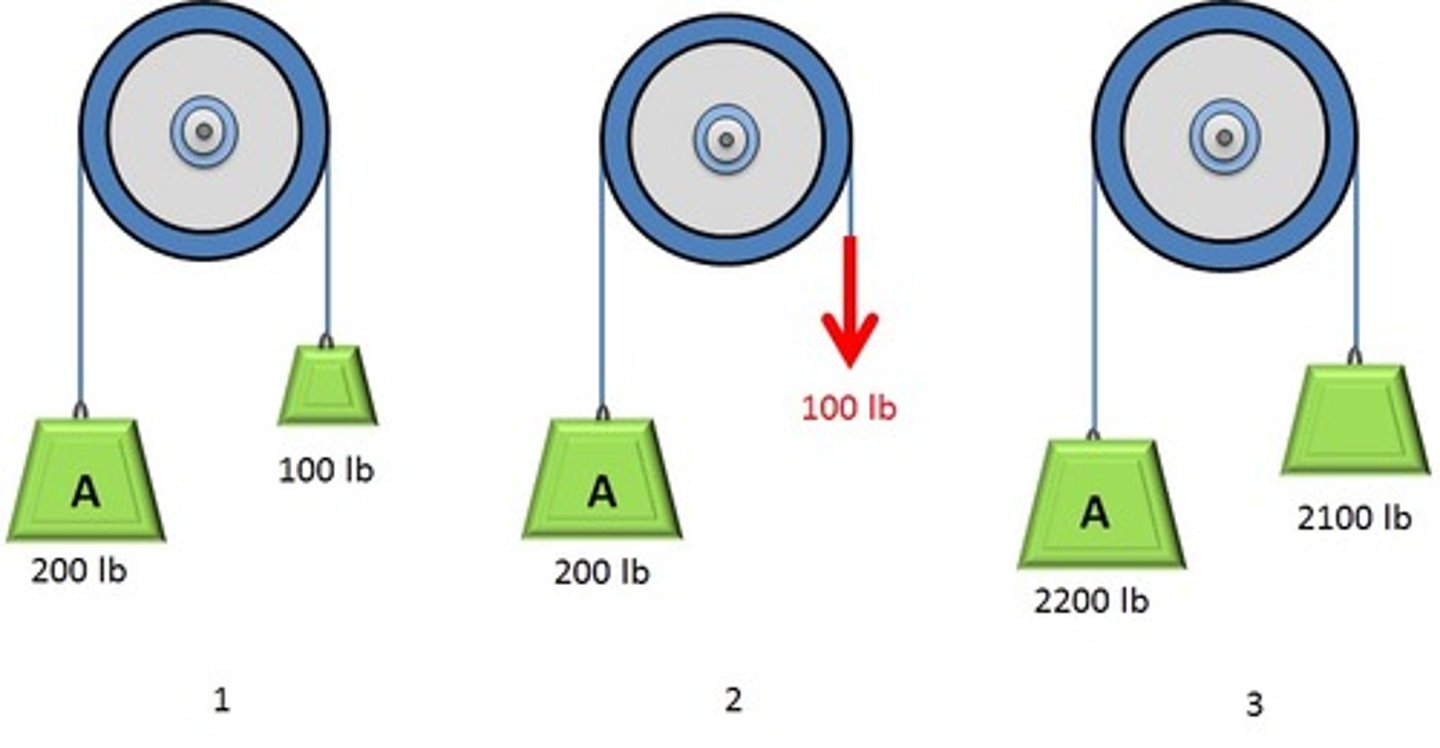
In which case does mass A have the largest acceleration?

Case 2

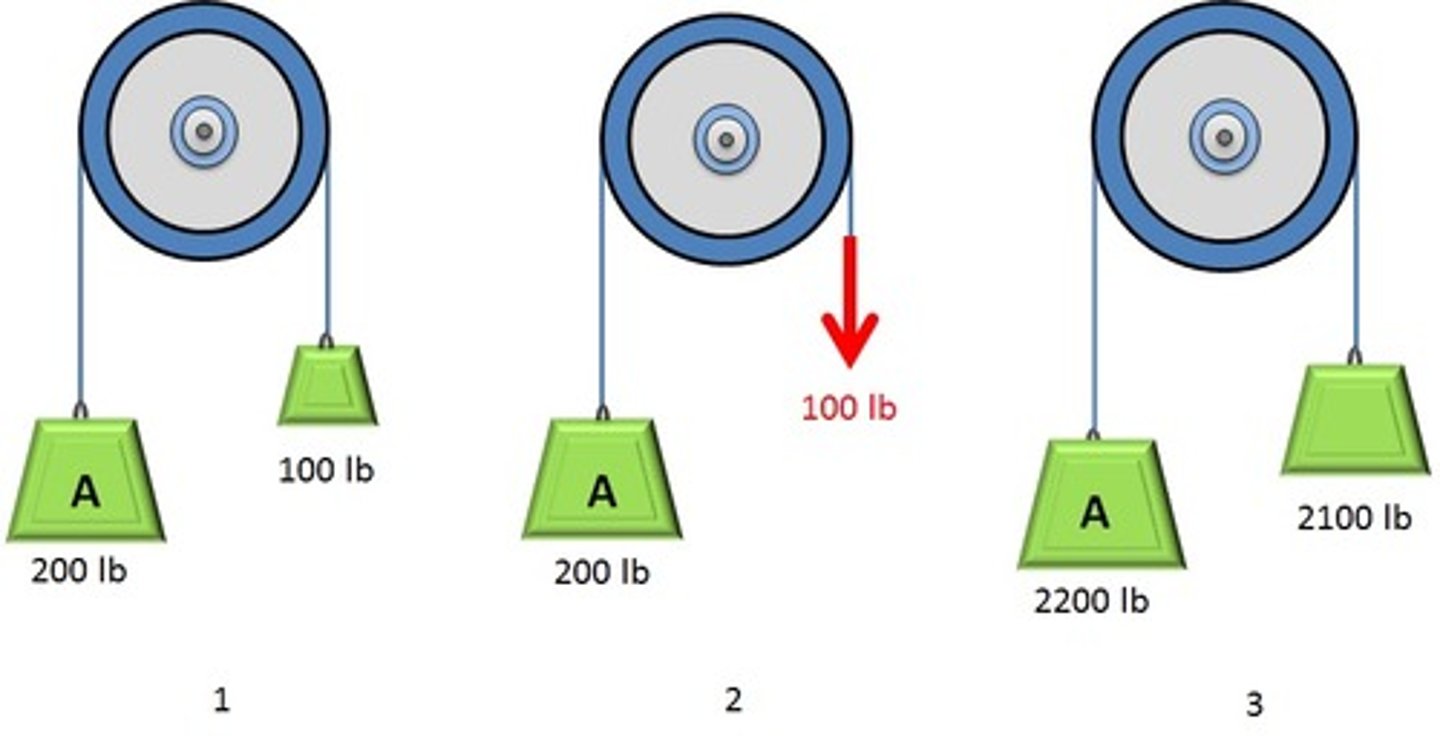
In which case does mass A have the smallest acceleration?

Case 3

Suppose two blocks are places on a moving belt, next to each other, with different coefficients of friction for each block - say 0.3 for the one in the front and 0.5 for the one behind.

The belt is given an acceleration of 0.4g. What happens and why?

Front one wants to slip, the back one does not -- slipping or not depends on the relative masses

Suppose a block is placed on a surface, with a friction coefficient of 0.25. The surface is then given a sudden acceleration. Pick the right answer

If there are no other forces or objects touching it, it will slip if belt moves with acceleration larger than 0.25g

In high speed slights, what is the `g force' in a circular path?

it is the inertial force perpendicular to plane velocity

Assume there is NO friction between the bracket A and the ground or at the pulleys but there IS friction between bracket A and mass B. Assume mass C is quite small. Pick the two correct statements:

1. Direction of friction on mass B is to the right

2. No matter how small the mass of C, the bracket will move

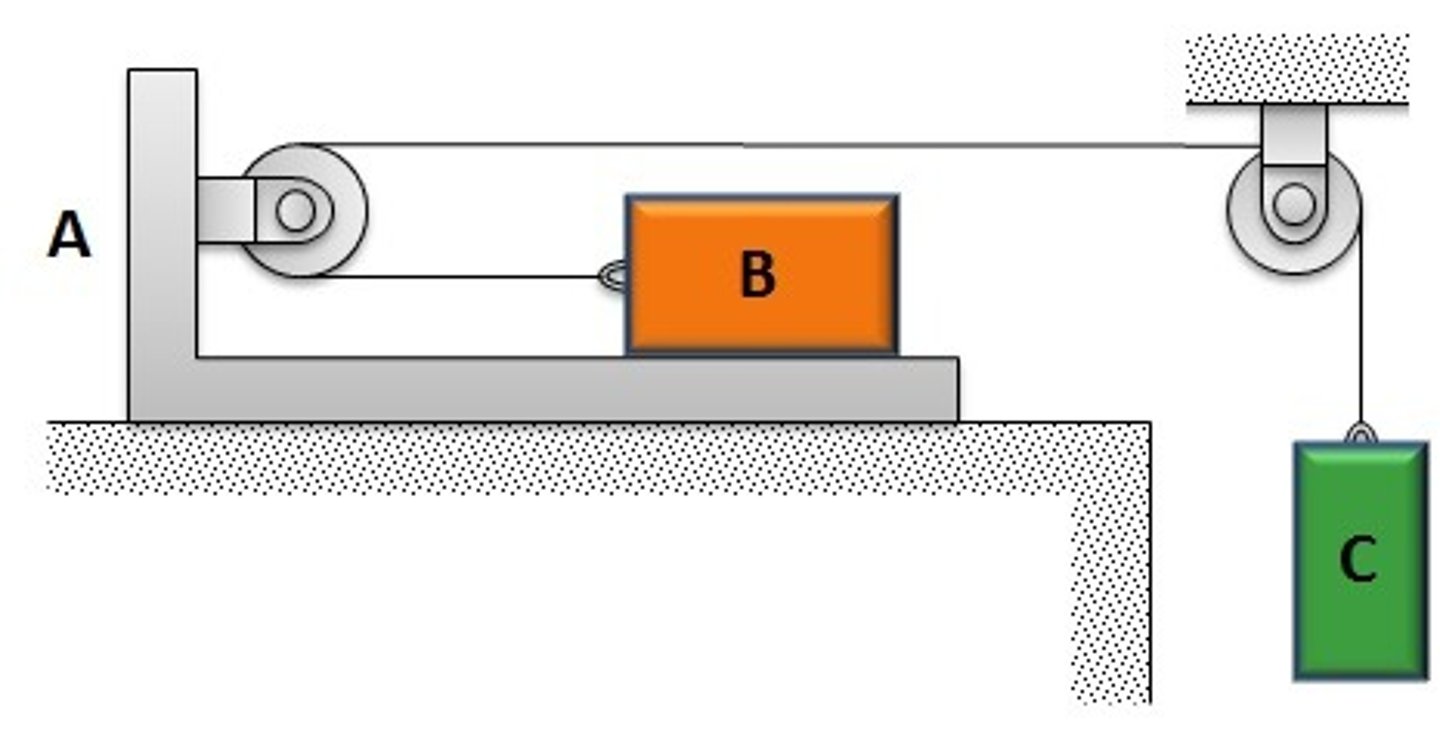
For the same figure, we slowly increase the mass of C. Pick the two correct answers

1. Slippage between A and B occurs once the friction cannot keep A and B together while staying less than (or equal to) mu * m_B g (mu is the coeff of friction).

2. If B moves with respect to A, it could have a leftward relative velocity

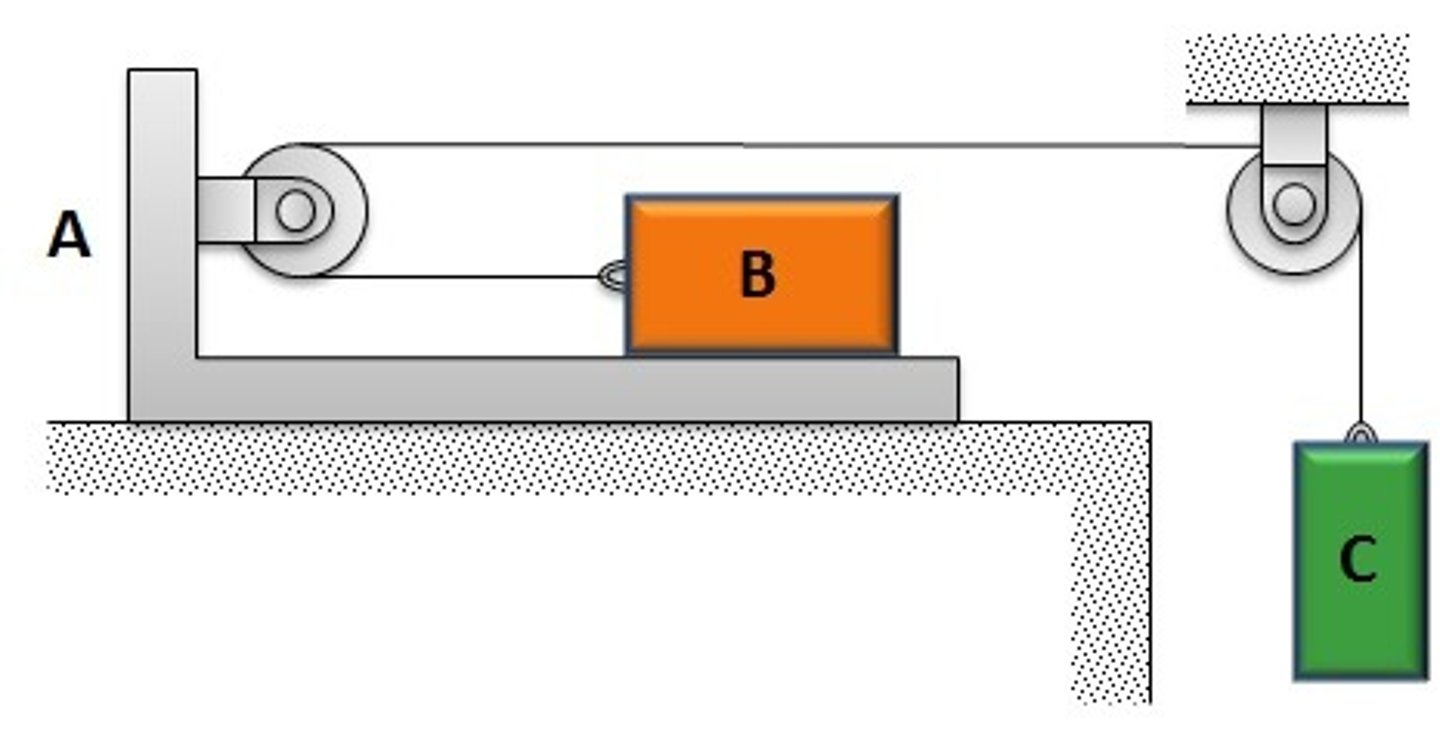
For the same figure: Now we use a rough surface between the bracket A and the support surface (same mu on both surfaces). Pick the two right answers.

1. Total forces on the mass B are the tension T to the left and friction to the right

2. Total forces on the bracket are 2T to the right and two friction forces (one on each surface) to the left