4. T-tests Pt2

What defines an independent-samples design, and how is it used in psychology?

• Subjects in each group are not matched.

• Groups are independent (e.g., control vs experimental).

• Typical research process:

  1. Randomly sample subjects.

  2. Randomly assign to control/experimental group.

  3. Compare group means on the dependent variable.

• Used widely in between-subjects experiments.

How else can independent samples be formed besides random assignment?

• Randomly sample from pre-existing groups.

  • Example: only-children vs first-borns (with younger siblings).

• Steps:

  1. Select participants from each group.

  2. Administer test of interest.

  3. Compare means between groups.

• Rationale: compare natural categories when manipulation isn’t possible.

• Think-pair-share question: Why only “oldest child” vs “only child”? → To isolate sibling-effect without mixing birth-order confounds.

What are the three main types of t-tests and when are they used?

• One-sample t-test: Compare sample mean X-bar to known population mean μ

• Dependent (paired) t-test: Compare mean of differences D-bar between matched or repeated measures.

• Independent t-test: Compare means of two independent groups X1 - X2

• All use:

  • Numerator = observed difference.

  • Denominator = standard error of that difference.

  • Logic: signal (effect) ÷ noise (variation).

What does the denominator represent in an independent-sample t-test?

• It’s the variance of the difference in sample means.

• Equivalent to: Standard Error of the Difference (SED).

• This is the SD of the sampling distribution of differences between two independent group means.

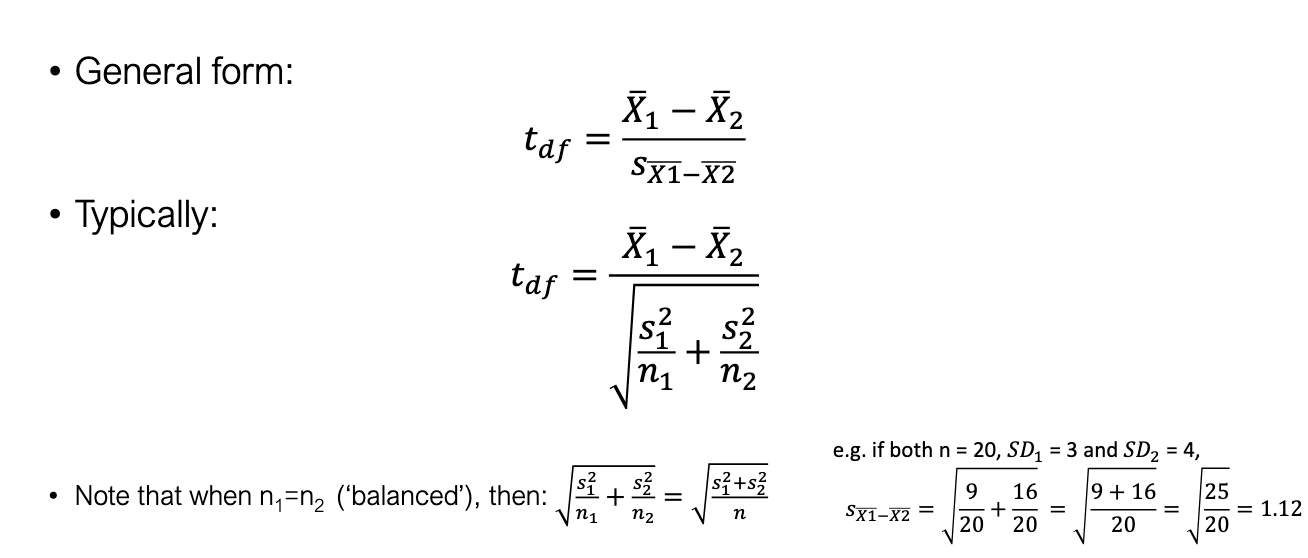
• Formula (general):

  

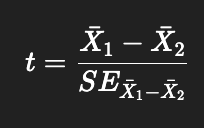
What is the denominator in the independent t-test called, and why is it important?

• Standard error of the difference between means (SED).

• Captures how much difference we expect by chance.

• Smaller SE → easier to detect real group differences.

• Denominator is the key to making inference valid.

How does the variance sum law apply to the independent-samples t-test?

• Law: Var(X ± Y) = Var(X) + Var(Y), if X & Y are independent.

• Applied to means:

  

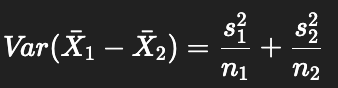
• Taking square root gives standard error of difference.

• Explains why both group variances contribute to denominator.

How do we compute the variance of the difference in sample means?

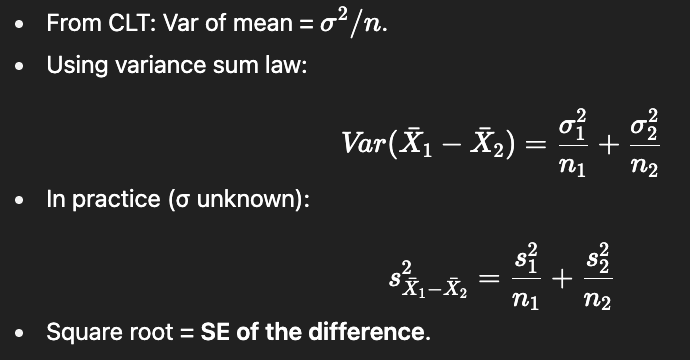
What is the formula for the independent t-statistic using group variances?

• Numerator = mean difference.

• Denominator = standard error of difference.

• Shows difference in relation to variability.

  

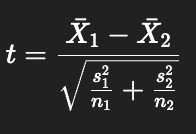
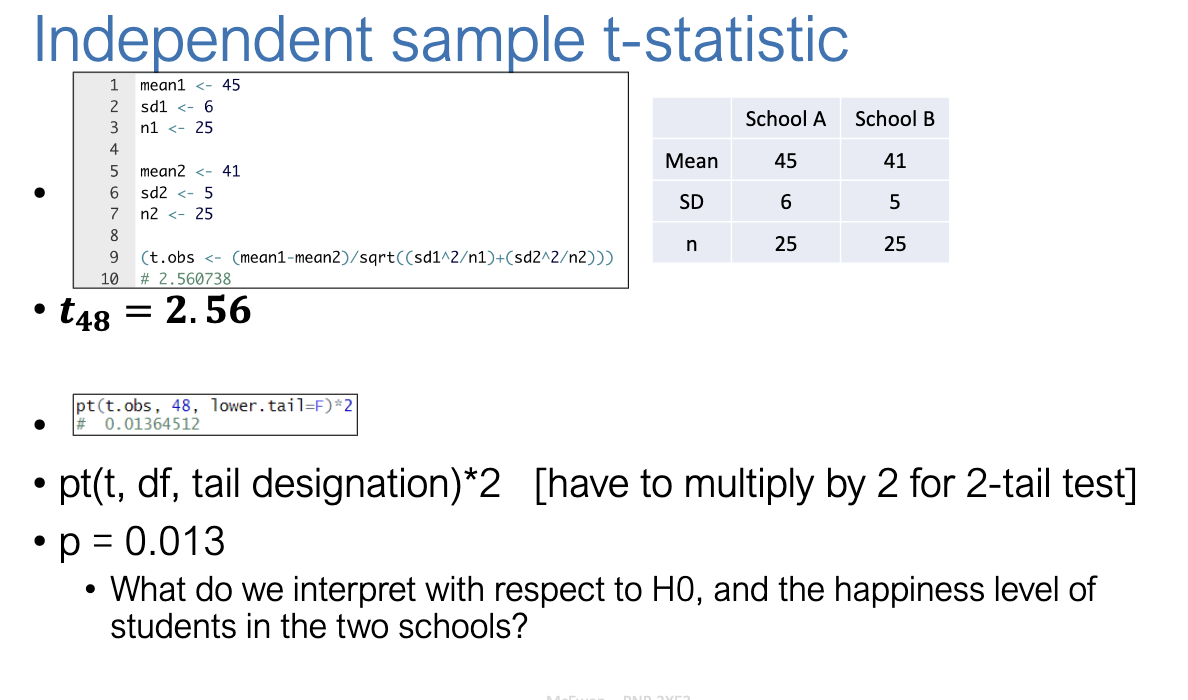
How do we set up an independent t-test with two groups (School A vs School B)?

• School A: X-bar=45, s=6, n=25

• School B: X-bar=41, s=5, n=25

• Steps:

  1. State hypotheses: H0:μ1=μ and H1:μ1≠μ2

  2. Compute mean difference = 4.

  3. Compute SE using formula.

  4. Calculate t.

  5. Compare with critical value or p-value.

What does the result of the happiness study tell us?

• Obtained statistic: t(48)=2.56

• p = 0.013 (two-tailed).

• Interpretation: Reject H0

• Students’ happiness differs significantly between schools.

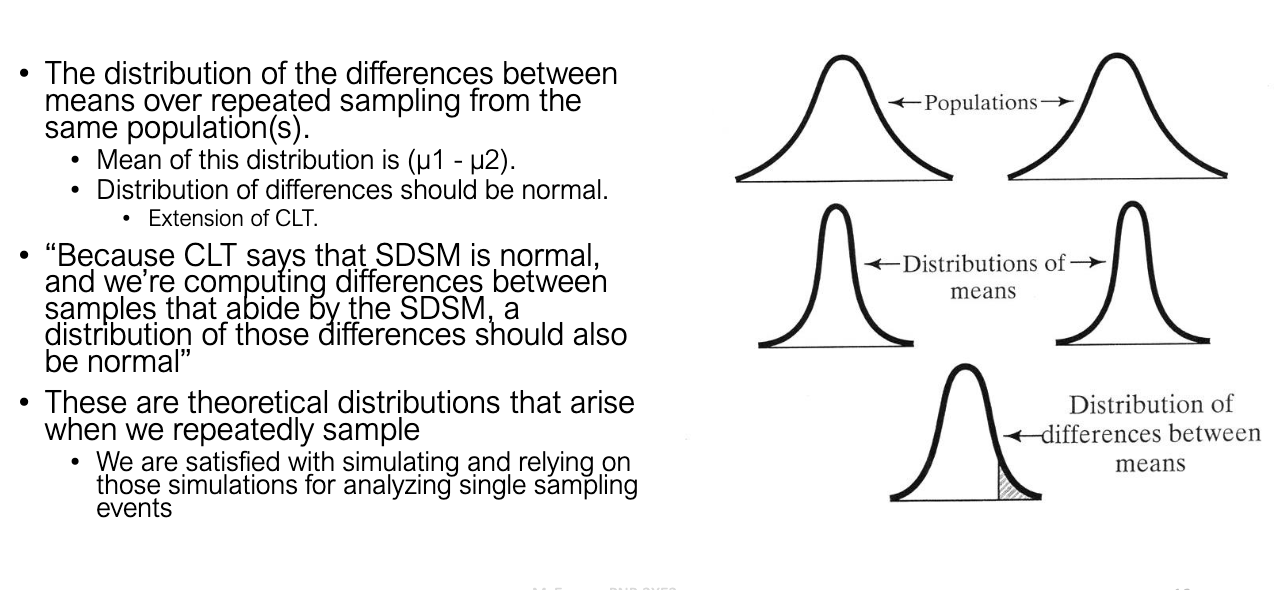
What is the distribution of differences between means?

• It’s the sampling distribution of X1-X2

• Center = μ1−μ2

• Shape ≈ normal (by CLT).

• Spread = SE of difference.

• Important: this is the theoretical distribution against which our observed difference is tested.

How do we get from populations to the distribution of mean differences?

• Process:

  1. Sample repeatedly from population 1 → distribution of means.

  2. Sample repeatedly from population 2 → distribution of means.

  3. Subtract group means for each pair of samples.

  4. Result = distribution of differences between sample means.

• That’s the reference distribution for the independent t-test.

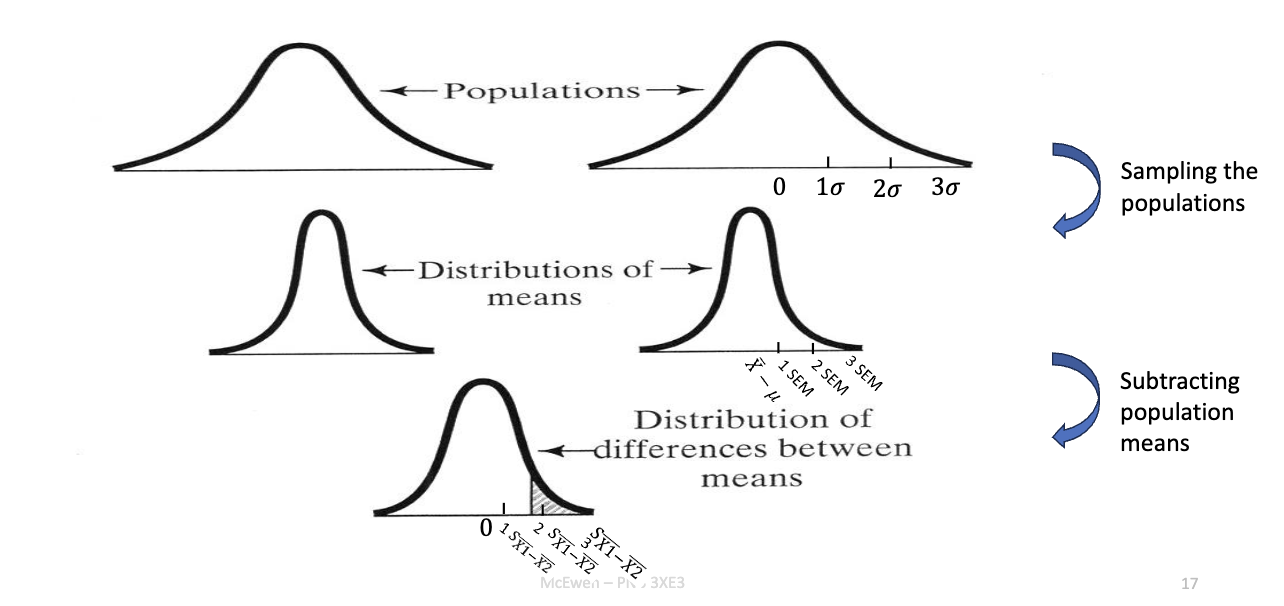
What defines the distribution of differences between means in t-tests (independent samples t-test)?

• Center: observed mean difference X1-X2

• Width: standard error s_X1-X2

• Test statistic:

  

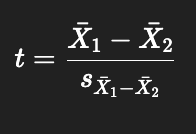
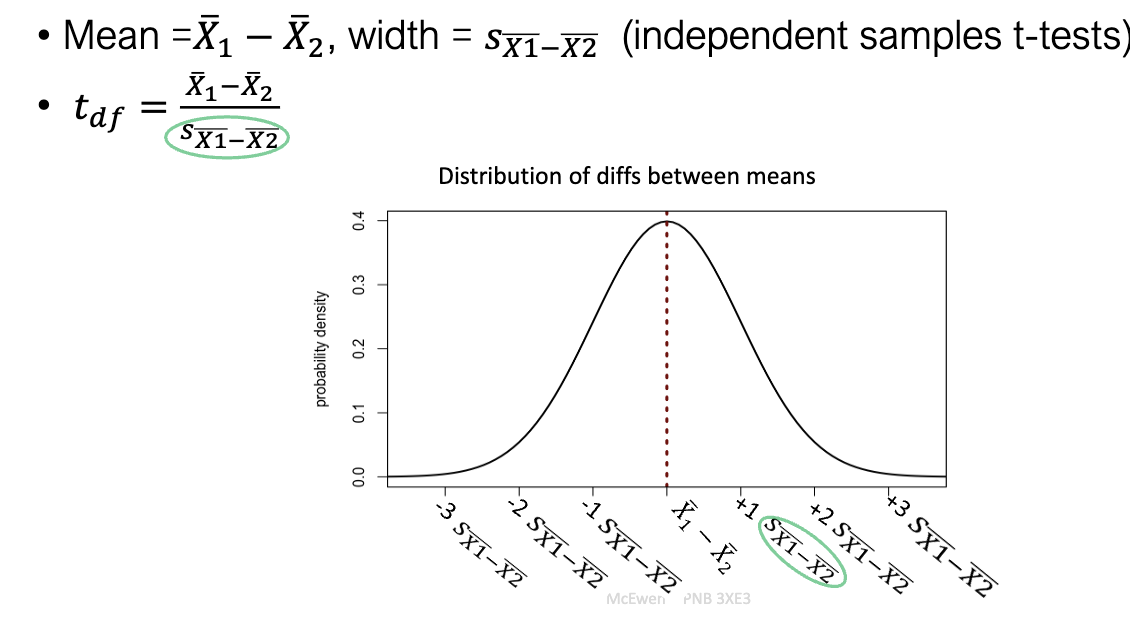
What is the general form of the independent t-test?

Why do we use pooled variance when sample sizes are unequal?

• Unequal n → SE formula can overweight one group’s variance.

• Solution: use pooled variance (weighted average of group variances).

• Weights each variance by its df, giving fairer estimate of true variance.

Formula:

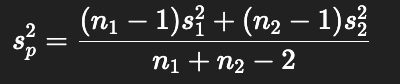
When should we use pooled variance?

• Use if:

  • S²₁ ≈ S²₂ (similar variances, less than 4× different).

  • Especially when n1≠n2

• Don’t pool if:

  • Variances differ a lot (≥4×).

• If n1=n2, pooled variance = simple average of group variances.

How does the independent t-test formula change with pooled variance?

Replace each variance with pooled variance:

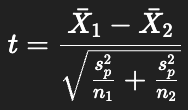
• If variances are similar and n1≠n2​ → use pooled.

• If variances are too different → don’t pool.

• If variances similar & n1=n2​ → either method works (same result).

What happens when sample sizes are equal?

Pooled variance simplifies to:

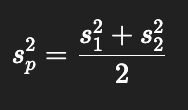
• Just the average variance.

• With equal n, pooled and non-pooled give identical t.

How is the DrugX experiment set up for an independent t-test?

• IV: Drug condition (DrugX vs Placebo).

• DV: Number of maze errors (lower = better).

• Group 1 (DrugX): X-bar = 14, n=9

• Group 2 (Placebo): X-bar=16, n=10

• H0:μ1=μ2

• H1:μ1≠μ2

What are the null and alternative hypotheses for DrugX?

• H0​: μ1=μ2​ → Drug has no effect.

• H1​: μ1≠μ2​ → Drug does affect learning.

• Inference: Reject or fail to reject based on t-test outcome.

What formula is used for the DrugX study’s t-test?

What are the key descriptive stats for the DrugX groups?

• Group 1 (DrugX): n=9, X-bar=14, s²=23.25

• Group 2 (Placebo): n=10, X-bar=16, s²=15.78

• Hypotheses:

  • H0: No difference in errors.

  • H1: Difference exists.

• Data collected: number of maze errors (lower = better).

Why must pooled variance be used in the DrugX example?

• Sample sizes unequal (n=9 vs n=10).

• Variances similar (ratio < 4).

• Rule: with unequal n and similar variances → must pool.

What are the calculated statistics for the DrugX example?

• Pooled variance: sp2=19.3

• Standard error: SE=2.02

• Observed t: t=−0.99

• df = 17.

• Group 1: X-bar=14.

• Group 2: X-bar=16

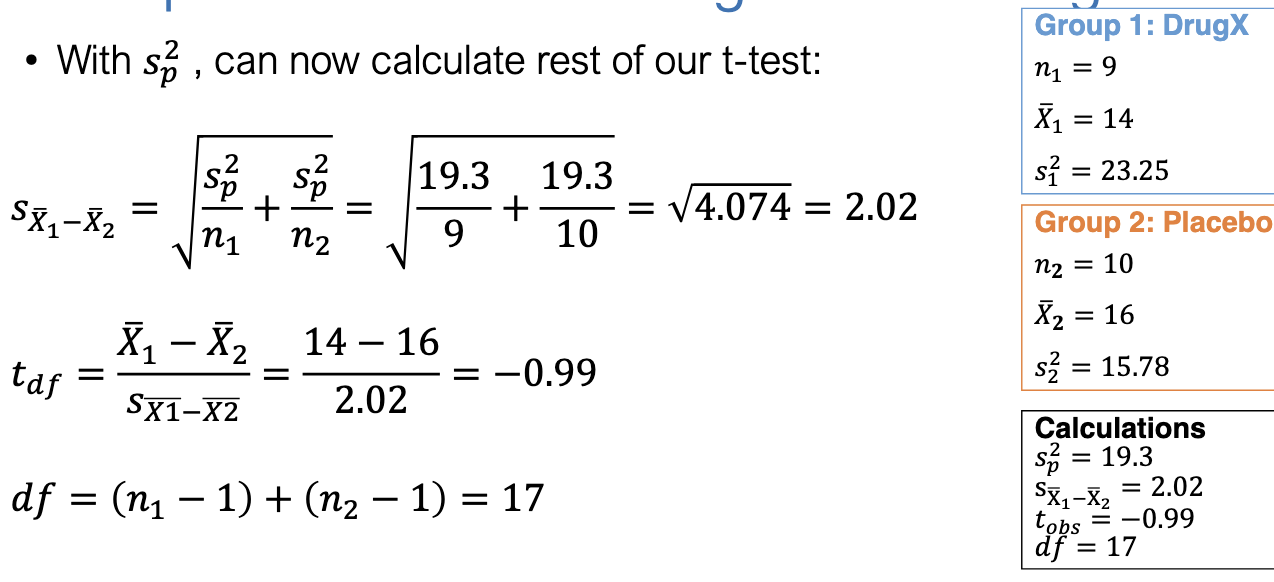
What does the t-test reveal about DrugX’s effect on learning?

• tobs=−0.99

• Critical t (df=17, α=0.05, 2-tailed) = ±2.11.

• ∣tobs∣<tcrit→ fail to reject H0.

• Conclusion: No significant evidence DrugX affects maze learning errors.

• p-value confirms (p > .05).

How do we compute a 95% confidence interval for an independent t-test?

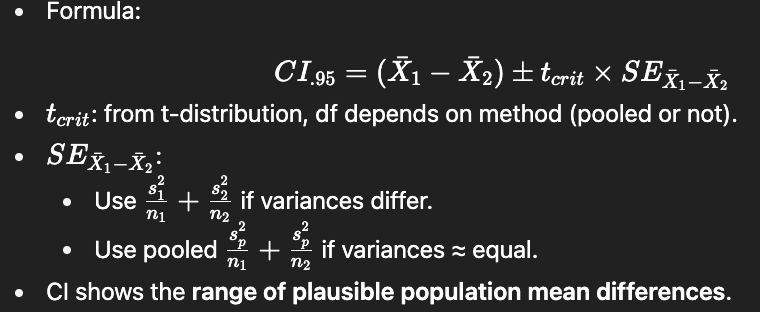
What did the 95% CI for the DrugX study show, and what does it mean?

• Calculation: 

• CI includes 0 → difference could plausibly be 0.

• Interpretation: Fail to reject H0H_0H0​.

• Conclusion: No evidence DrugX significantly changed maze errors.

What is the “homogeneity of variance” assumption in t-tests?

• Assumption: population variances equal (σ²₁=σ²₂)

• If violated → “heterogeneity of variance.”

• Rule of thumb: difference ≥ 4× → too different → don’t pool variances.

• If heterogeneous: use separate variance formula instead of pooled.

What are the three main assumptions of an independent-sample t-test?

• Equal variances (homogeneity).

  • Even if means differ, assume variances are the same.

• Normality.

  • Group means should come from normal populations.

  • CLT helps if n ≥ 30 per group; issue if very small n.

• Independence.

  • Individuals’ scores not related (no pairing)

Why use effect size with t-tests, and how is it calculated?

• Problem: p-values depend on sample size.

• Effect size gives a standardized difference, less sensitive to n.

• Formula:

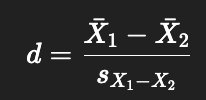
• Important: denominator = standard deviation of differences, not standard error.

• Uses variance sum law for calculation.

How do we compute Cohen’s d for independent samples?

How was the mindfulness/anxiety study designed?

• n=12 per group (low anxiety vs high anxiety).

• IV: Anxiety group.

• DV: Mindfulness (FFMQ scores).

• Hypotheses:

  • H0​: No difference in mindfulness.

  • H1: Groups differ in mindfulness.

What are the 5 steps of hypothesis testing (applied to mindfulness/anxiety)?

1. State hypotheses.

2. Choose test (independent t-test).

3. Gather what’s needed (means, variances, n, SE).

4. Calculate t and make decision.

5. Check effect size.

How do we choose the test and decide 1- vs 2-tailed for mindfulness/anxiety?

• Test: Independent t-test.

• Method:

  • Option 1: Compute tobs

  • Option 2: Compute CI.

• Tail: TWO-tailed (question is whether mindfulness differs, not directional).

What info do we need to compute tobs​ in mindfulness/anxiety?

• Group means (X1, X2)

• Group sizes (n1, n2)

• Variances (s²₁, s²₂)

• Decide: pool or not?

  • If n1=n2​ and variances ≈ equal → pool.

  • If variances ≥4× different → don’t pool.

How do we compute pooled variance for mindfulness/anxiety?

What is the observed t-value for mindfulness/anxiety?

What is the conclusion from the mindfulness/anxiety test?

• tobs=2.73​=2.73, p = 0.012 (< 0.05).

• Reject H0

• Conclusion: Low- and high-anxiety groups differ in mindfulness scores.

What is the effect size for mindfulness/anxiety, and how do we interpret it?