Topic 4 Series

Convergent Series

When partial sums approach a certain value; infinite series can only be evaluated if the series is convergent

Divergent Series

When the partial sums approach positive or negative infinity

Explicit Formula of an Arithmetic Sequence

Formula for Partial Sum of an Arithmetic Series

Sigma Notation for Arithmetic Series

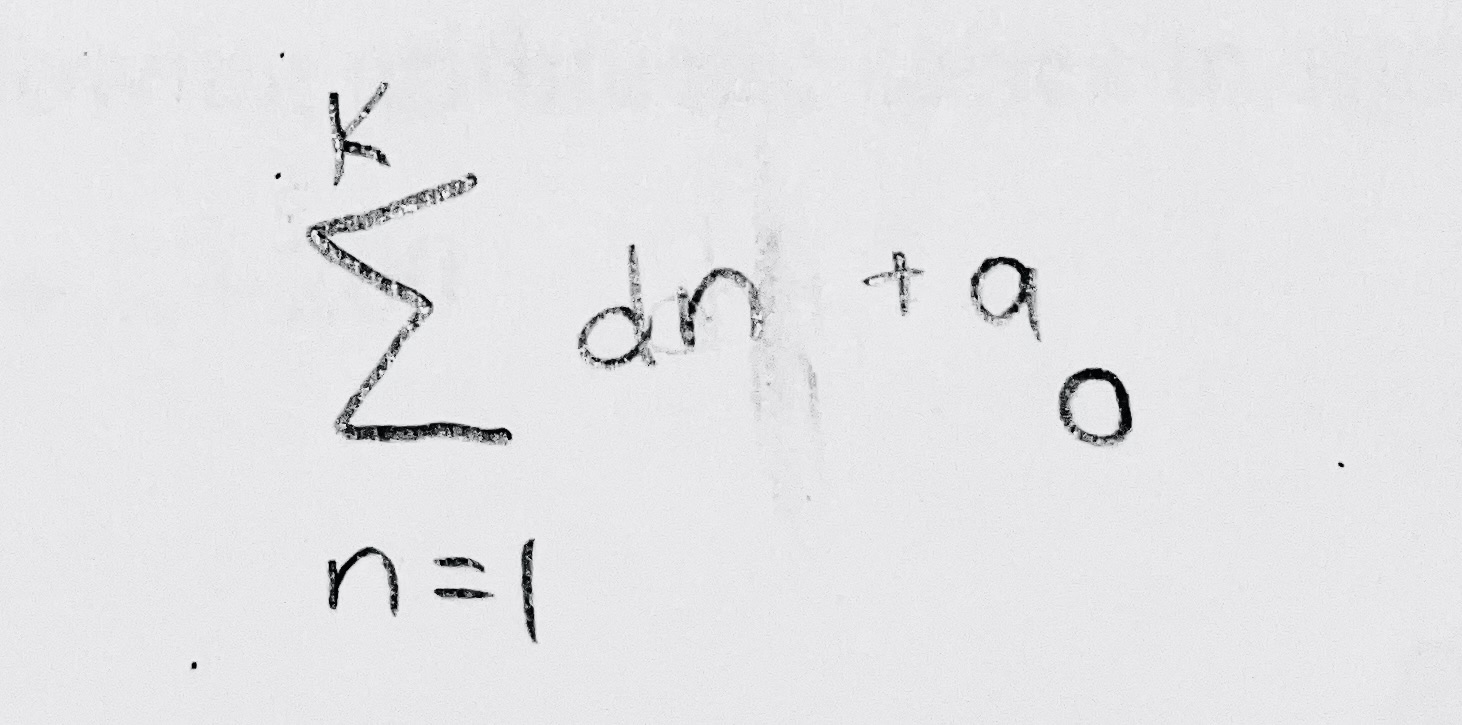
Arithmetic Series

Difference includes subtraction or addition; always divergent due to being linear

Geometric Series

Uses ratio instead of differences, multiplication and division; convergent when absolute value of ratio is less than one (fraction)

Explicit Formula of a Geometric Sequence

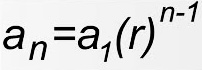
Sigma Notation of a Geometric Series

Partial Sum of a Geometric Sequence

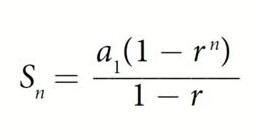
Sum of an Infinite Geometric Sequence

SSF: Series of a Constant

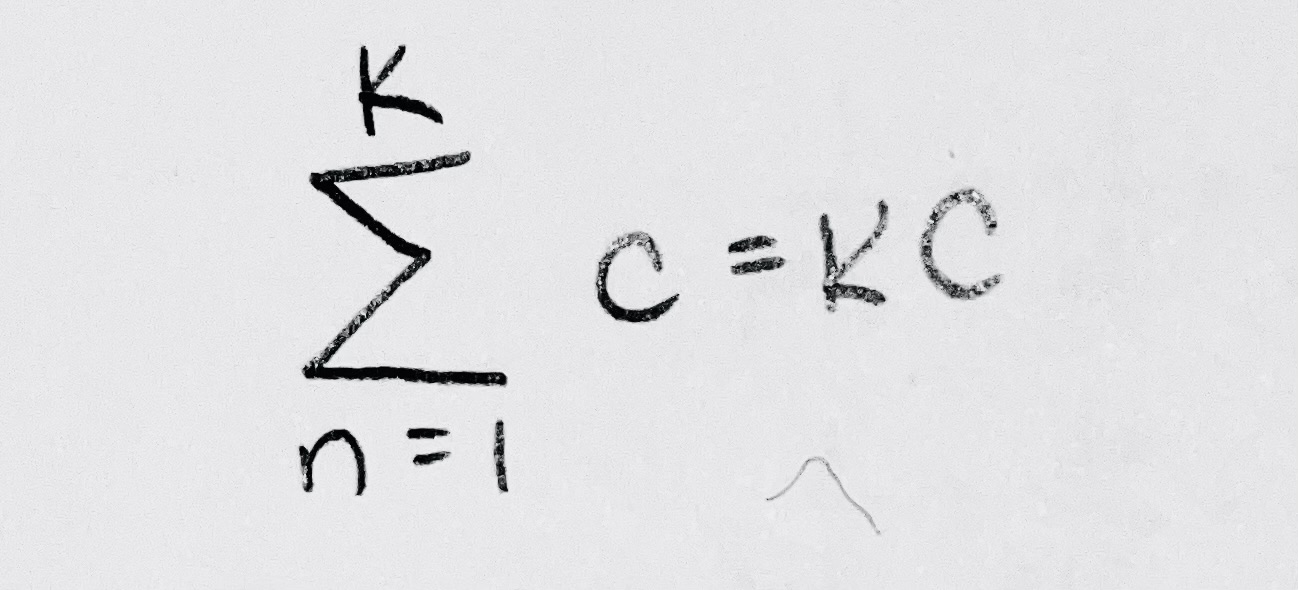
SSF: Positive Integers

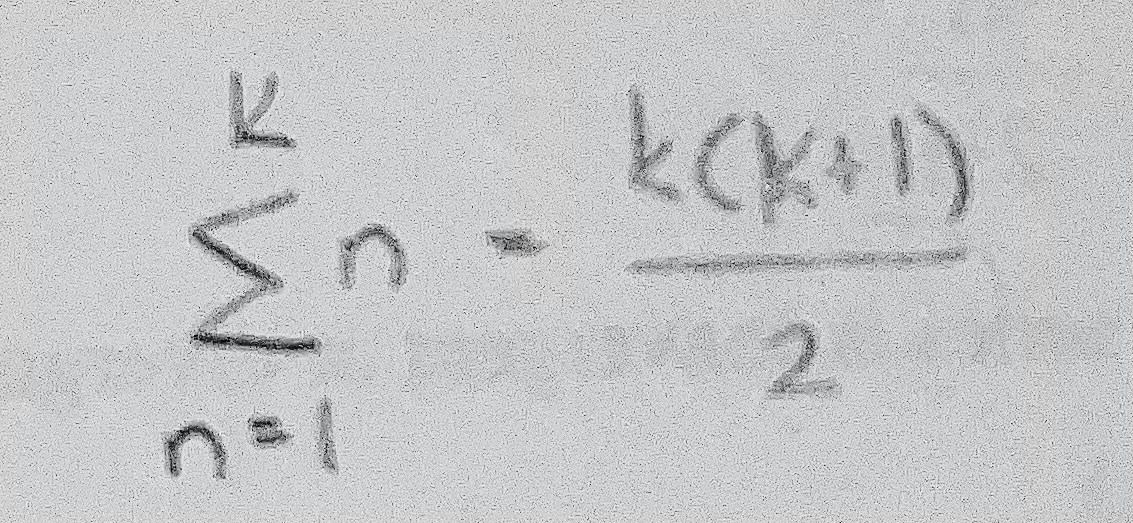
SSF: Squares of Positive Integers

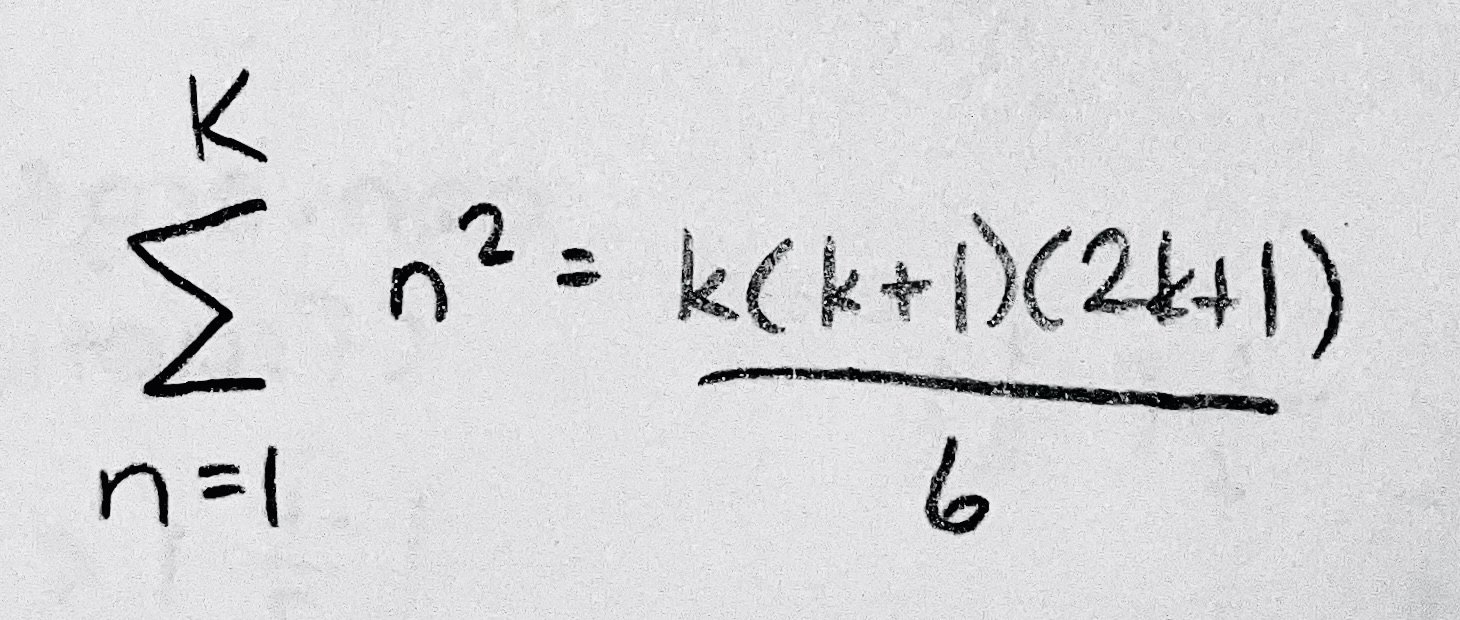
SSF: Cubes of Positive Integers