AP Calculus AB Flashcards

Volume of Sphere

\frac43\pi r^2

Volume of rectangular prism/cube

lwh

Volume of cone

\frac{\pi r^2h}{3}

volume of cylinder

\pi r^2h

area of right triangle

\frac12bh

area of semi-circle

\frac{\pi r^2}{2}

area of quarter-circle

\frac{\pi r^2}{4}

area of circle

\pi r^2

area of square

s^2

area of rectangle

wl

area of trapezoid

\frac{\left(a+b\right)}{2}h

equation of semi-circle function

\sqrt{r^2-\left(x-h\right)^2}+k , where the center of the circle is (h,k) and the radius is r

equation of a circle function

\left(x-h\right)^2+\left(y-k\right)^2=r^2 , where the center of the circle is (h,k) and the radius is r

distance formula

d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} (this is an application of the Pythagorean theorem!)

height of equilateral triangle and relation to 30-60-90 triangle

\frac{a\sqrt3}{2} , an equilateral triangle split in half is a 30-60-90 triangle

tangent line/point slope form

y_2-y_1=m\left(x_2-x_1\right)

local linearity

y-y_1=m\left(x-x_1\right)

tangent line

instantaneous rate of change (IROC): slope from one point

mean value theorem

f^{\prime}\left(c\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a} , IROC = AROC if… f(x) is continuous on [a,b] abd differentiable on (a,b), then somewhere IROC = AROC

first derivative tells you…

increasing/decreasing — first thing you notice from just looking at if f’(x) is neg/pos

definition of derivative

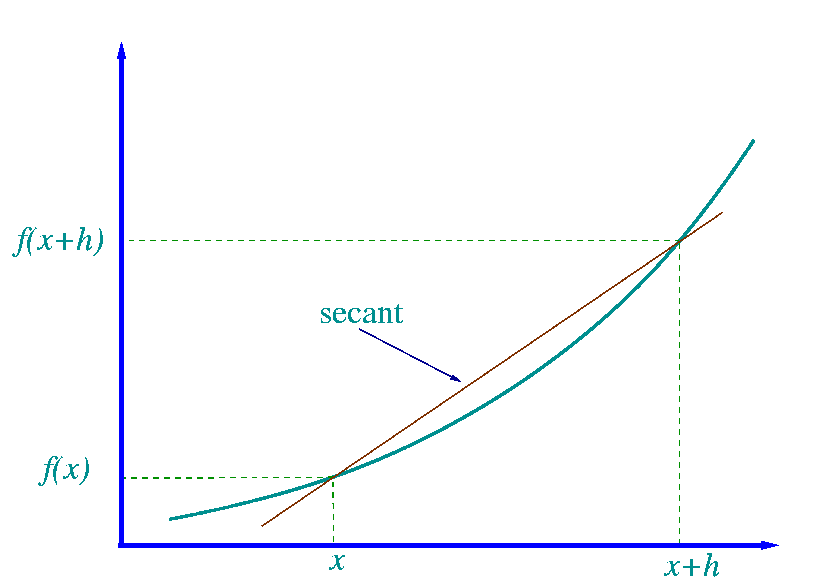
\lim_{h\rightarrow0}\frac{f\left(x+h\right)-f\left(x\right)}{h} , h= smallest gap from IROC you are solving for

secant line

AROC: slope from 2 points

infinite limit of sin(x)/x

\lim_{x\rightarrow\infty}\frac{\sin\left(x\right)}{x}=0\cup\lim_{x\rightarrow-\infty}\frac{\sin\left(x\right)}{x}=0

Differentiability

\lim_{x\rightarrow a^{-}}f\left(x\right)=\lim_{x\rightarrow a^{+}}f\left(x\right)=f\left(a\right) — continuous

\lim_{x\rightarrow a^{-}}f^{\prime}\left(x\right)=\lim_{x\rightarrow a^{+}}f^{\prime}\left(x\right) — smooth at x=a, right and left limits approaching the same value

definition of continuity

\lim_{x\rightarrow a^{-}}f\left(x\right)=\lim_{x\rightarrow a^{+}}f\left(x\right)=f\left(a\right)

intermediate value theorem

if f(x) s continue on [a,b] and k is any value between f(a) and f(b), then there is at least one value c in the interval [a,b] such that f (c ) = k

squeeze theorem

f\left(x\right)\le g\left(x\right)\le h\left(x\right)\cup\lim_{x\rightarrow C}f\left(x\right)=L,\lim_{x\rightarrow C}h\left(x\right)=L\Rightarrow\lim_{x\rightarrow C}g\left(x\right)=L

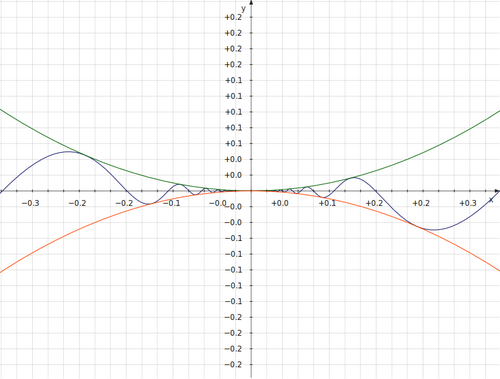
infinite limit: same degrees

\frac{x^2}{x^2}\rightarrow\frac{c}{c}=\lim_{x\rightarrow a}f\left(x\right)

infinite limit: higher degree in numerator

\frac{x^2}{x}\rightarrow\frac{big}{small}\rightarrow\lim_{x\rightarrow a}f\left(x\right)=\pm\infty

infinite limit: lower degree in numerator

\frac{x}{x^2}\rightarrow\frac{small}{big}\rightarrow\lim_{x\rightarrow a}f\left(x\right)=0

infinite/essential/asymptotic discontinuity

\lim_{x\rightarrow a^{-}}f\left(x\right)\ne\lim_{x\rightarrow a^{+}}f\left(x\right) AND one or both DNE (*can be continuous at other points)

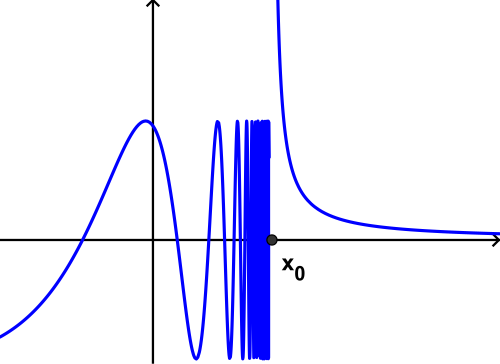
jump discontinuity

\lim_{x\rightarrow a^{-}}f\left(x\right)\ne\lim_{x\rightarrow a^{+}}f\left(x\right)

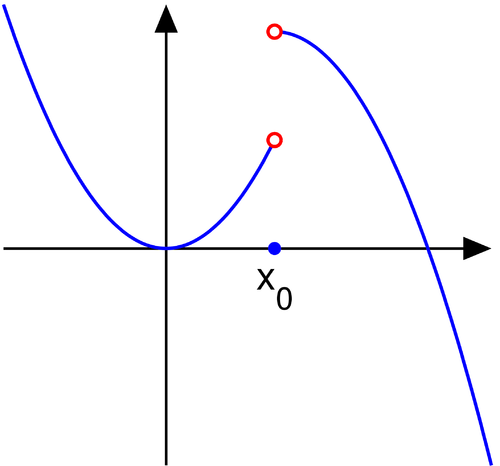
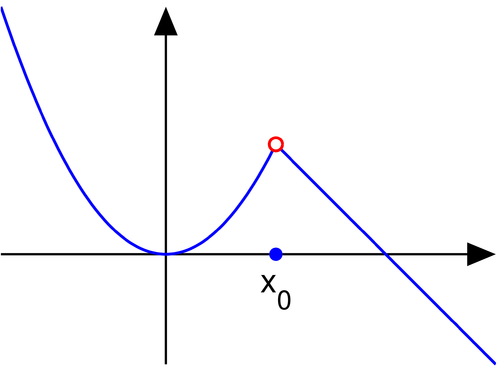
removable discontinuity

\lim_{x\rightarrow a}f\left(x\right)\ne f\left(a\right)

power rule of limits

\lim_{x\rightarrow a}\left\lbrack f\left(x\right)\right\rbrack^{n}=\left\lbrack\lim_{x\rightarrow a}f\left(x\right)\right\rbrack^{n}

root rule of limits (application of the power rule)

\lim_{x\rightarrow a}\left\lbrack\sqrt{f\left(x\right)}\right\rbrack=\lim_{x\to a}\left\lbrack f\left(x\right)\right\rbrack^{\left(\frac12\right)}=\left\lbrack\lim_{x\to a}f\left(x\right)\right\rbrack^{\left(\frac12\right)} a square root is the same as the power of 1/2, so you can adapt all radical functions using the power rule of limits

sum and difference rule of limits

\lim_{x\to a}\left\lbrack f\left(x\right)\pm g\left(x\right)\right\rbrack=\lim_{x\to a}f\left(x\right)\pm\lim_{x\to a}g\left(x\right)

constant multiple rule of limits

\lim_{x\to a}\left\lbrack cf\left(x\right)\right\rbrack=c\cdot\lim_{x\to a}f\left(x\right)

product rule of limits

\lim_{x\to a}\left\lbrack f\left(x\right)g\left(x\right)\right\rbrack=\lim_{x\to a}f\left(x\right)\cdot\lim_{x\to a}g\left(x\right)

quotient rule of limits

\lim_{x\to a}\left\lbrack\frac{f\left(x\right)}{g\left(x\right)}\right\rbrack=\frac{\lim_{x\to a}f\left(x\right)}{\lim_{x\to a}g\left(x\right)}

sum and difference rule of derivatives

\frac{d}{\differentialD x}f\left(x\right)\pm g\left(x\right)=f^{\prime}\left(x\right)\pm g^{\prime}\left(x\right)

product rule of derivatives

\frac{\differentialD y}{\differentialD x}\left\lbrack f\left(x\right)\cdot g\left(x\right)\right\rbrack=f\left(x\right)\cdot g^{\prime}\left(x\right)+f^{\prime}\left(x\right)\cdot g\left(x\right)

quotient rule of derivatives

\frac{\differentialD y}{\differentialD x}\left\lbrack\frac{f\left(x\right)}{g\left(x\right)}\right\rbrack=\frac{g\left(x\right)\cdot f^{\prime}\left(x\right)-f\left(x\right)\cdot g^{\prime}\left(x\right)}{\left\lbrack g\left(x\right)\right\rbrack^2}

chain rule

\frac{\differentialD y}{\differentialD x}\left\lbrack f\left(g\left(x\right)\right)\right\rbrack=f^{\prime}\left(g\left(x\right)\right)\cdot g^{\prime}\left(x\right)

l’hopitals rule

\lim_{x\to a}\frac{f\left(x\right)}{g\left(x\right)}=\frac00\cap\frac{\infty}{\infty}\Rightarrow\lim_{x\to a}\frac{f^{\prime}\left(x\right)}{g^{\prime}\left(x\right)}=L

first derivative test

tells you relative extrema. plug in numbers on either side of candidates, pos to negative = maximum, neg to positive = minimum

second derivative test

tells you relative extrema. plug in candidates to f’’(x), if positive = minimum, if negative = maximum

\frac{\differentialD p}{\differentialD t}=kt\ldots

\ldots P=P_0e^{rt}

volumes of revolution formula

\pi\int_{a}^{b}\left(f\left(x\right)-a\right)^2-\left(g\left(x\right)-a\right)^2\differentialD x

area between curves formula (terms of x)

\int_{a}^{b}f\left(x\right)-g\left(x\right)\differentialD x

area between curves formula (terms of y)

\int_{c}^{d}f\left(y\right)-g\left(y\right)\differentialD y

indefinite integral

\int_{\placeholder{}}^{\placeholder{}}f\left(x\right)dx

definite integral

\int_{a}^{b}f\left(x\right)\differentialD x

average value formula

\frac{1}{b-a}\int_{a}^{b}f\left(x\right)\differentialD x

fundamental theorem of calculus part one

\frac{\differentialD y}{\differentialD x}\int_{a}^{t}f\left(x\right)\differentialD x=f\left(t\right) , derivatives and integrals are inverse operations

fundamental theorem of calculus part two

\int_{a}^{b}f\left(x\right)\differentialD x=F\left(b_{}\right)-F\left(a\right)

extreme value theorem

If a function is continuous on [a,b], then it must have a maximum and a minimum on that interval.

power rule of derivatives

\frac{\differentialD y}{\differentialD x}x^{n}=nx^{n-1}

reverse power rule of integrals

\int_{a}^{b}x^{n}dx=\frac{1}{n+1}x^{n+1}

\frac{\differentialD y}{\differentialD x}\log_{a}x

\frac{1}{\ln\left(a\right)\cdot x}

\frac{\differentialD y}{\differentialD x}a^{x}

a^{x}\cdot\ln\left(a\right)

\frac{\differentialD y}{\differentialD x}\sin^{-1}\left(x\right)

\frac{1}{\sqrt{1-x^2}}

\frac{\differentialD y}{\differentialD x}\cos^{-1}\left(x\right)

\frac{-1}{\sqrt{1-x^2}}

\frac{\differentialD y}{\differentialD x}\csc^{-1}\left(x\right)

\frac{-1}{\left\vert x\right\vert\sqrt{\left(x^2-1\right)}}

\frac{\differentialD y}{\differentialD x}\sec^{-1}\left(x\right)

\frac{1}{\left\vert x\right\vert\sqrt{\left(x^2-1\right)}}

\frac{\differentialD y}{\differentialD x}\cot^{-1}\left(x\right)

\frac{-1}{1+x^2}

\frac{\differentialD y}{\differentialD x}\tan^{-1}\left(x\right)

\frac{1}{1+x^2}