Bstats

exam 1

Which of the following is an example of quantitative data?

	the player’s number on a baseball uniform
	the serial number on a one-dollar bill
	the part number of an inventory item
	the number of people in a waiting line

the number of people in a waiting line

Which of the following is NOT an example of descriptive statistics?

	a histogram depicting the age distribution for 30 randomly selected students
	an estimate of the number of Alaska residents who have visited Canada
	a table summarizing the data collected in a sample of new-car buyers
	the proportion of mailed-out questionnaires that were returned

an estimate of the number of Alaska residents who have visited Canada

Which of the following is an example of categorical data?

	social security number
	score on a multiple-choice exam
	height, in meters, of a diving board
	number of square feet of carpet

social security number

The number of observations in a complete data set having 10 elements and 5 variables is _____.

	5
	10
	25
	50

10

The entities on which data are collected are _____.

	elements
	populations
	sets
	samples

elements

The set of measurements collected for an element is called a(n) _____.

	census
	variable
	observation
	sample

observation

A characteristic of interest for the elements is called a(n) _____.

	sample
	data set
	variable
	observation

variable

All data collected in a study are referred to as the _____.

	census
	inference
	variable
	data set

data set

In a data set, the number of observations will always be the same as the number of _____.

	variables
	elements
	data sets
	data

elements

Quantitative data _____.

	are always nonnumeric
	may be either numeric or nonnumeric
	are always numeric
	are always labels

are always numeric

Categorical data _____.

	are always nonnumeric
	may be either numeric or nonnumeric
	are always numeric
	indicate either how much or how many

may be either numeric or nonnumeric

Arithmetic operations are inappropriate for _____.

	categorical data
	quantitative data
	both categorical and quantitative data
	large data sets

categorical data

In a questionnaire, respondents are asked to mark their gender as Male, Female, Transgender MtoF, Transgender FtoM, Non-binary, or Intersex. Gender is an example of a(n) _____ variable.

categorical

In a questionnaire, respondents are asked to record their age in years. Age is an example of a _____.

quantitative variable

The graph below best exemplifies a _____.

       

	bar graph
	time series graph
	cross-sectional graph
	line graph

time series graph

The collection of all elements of interest in a study is _____.

	the population
	the sampling
	statistical inference
	descriptive statistics

the population

A portion of the population selected to represent the population is called _____.

	statistical inference
	descriptive statistics
	a census
	a sample

a sample

In a sample of 800 students in a university, 160, or 20%, are Business majors. Based on the above information, the school's paper reported, "20% of all students at the university are Business majors." This report is an example of _____.

	a sample
	a population
	statistical inference
	descriptive statistics

statistical inference

Six hundred residents of a city are polled to obtain information on voting intentions in an upcoming city election. The 600 residents in this study is an example of a(n) _____.

	census
	sample
	observation
	population

sample

A statistics professor asked students in a class their ages. Based on this information, the professor states that the average age of students in the university is 21 years. This is an example of _____.

	a census
	descriptive statistics
	an experiment
	statistical inference

statistical inference

In a recent study based upon an inspection of 200 homes in Daisy City, 120 were found to violate one or more city codes.

Refer to Exhibit 1-1. The Daisy City study is an example of the use of a _____.

	census
	sample
	probability
	population

sample

In a recent study based upon an inspection of 200 homes in Daisy City, 120 were found to violate one or more city codes.

Refer to Exhibit 1-1. The manager's statement that 60% of Daisy City's 3,000 homes are in violation of city codes is _____.

	an accurate statement
	only an approximation, since it is based upon sample information
	obviously wrong, since it is based upon a study of only 200 homes
	None of the other answers is correct.

only an approximation, since it is based upon sample information

In a sample of 3,200 registered voters, 1,440, or 45%, approve of the way the president is doing his job.

Refer to Exhibit 1-2. The 45% approval is an example of _____.

	a sample
	descriptive statistics
	statistical inference
	a population

descriptive statistics

In a sample of 3,200 registered voters, 1,440, or 45%, approve of the way the president is doing his job.

Refer to Exhibit 1-2. A political pollster states, "Forty five percent of all voters approve of the president." This statement is an example of _____.

	a sample
	descriptive statistics
	statistical inference
	a population

statistical inference

The sum of the relative frequencies for all classes will always equal _____.

	the sample size
	the number of classes
	1
	100

1

The height and weight are recorded by the school nurse for every student in a school. What type of graph would best display the relationship between height and weight?

	bar graph
	stem-and-leaf plot
	histogram
	scatter diagram

scatter diagram

In a cumulative frequency distribution, the last class will always have a cumulative frequency equal to _____.

	1
	100%
	the total number of elements in the data set
	None of the answers is correct.

the total number of elements in the data set

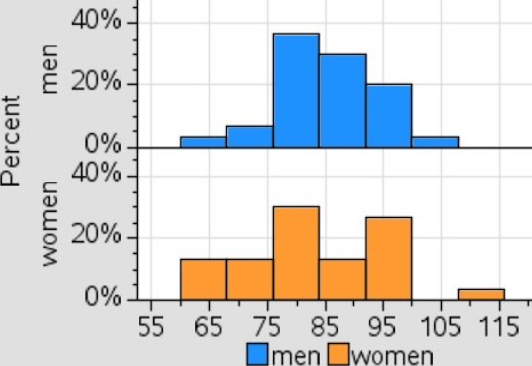
College students were surveyed to determine how much they planned to spend in various categories during the upcoming academic year.  One category is the amount spent on school supplies. The graphs below show the amount of money spent on school supplies by women and men.

5

The numbers of hours worked (per week) by 400 statistics students are shown below.

	Number of Hours	Frequency
	0x10	20
	10x20	80
	20x30	200
	30x40	100

​

Refer to Exhibit 2-1. The class width for this distribution _____.

is 10

The numbers of hours worked (per week) by 400 statistics students are shown below.

	Number of Hours	Frequency
	0x10	20
	10x20	80
	20x30	200
	30x40	100

​

Refer to Exhibit 2-1. The number of students working less than 20 hours is _____.

100

The numbers of hours worked (per week) by 400 statistics students are shown below.

	Number of Hours	Frequency
	0x10	20
	10x20	80
	20x30	200
	30x40	100

​

Refer to Exhibit 2-1. The relative frequency of students working less than 10 hours is _____.

0.05

The numbers of hours worked (per week) by 400 statistics students are shown below.

	Number of Hours	Frequency
	0x10	20
	10x20	80
	20x30	200
	30x40	100

​

Refer to Exhibit 2-1. The cumulative relative frequency for the class of 20

≤ x ≥ 30 is _____.

0.75

The numbers of hours worked (per week) by 400 statistics students are shown below.

	Number of Hours	Frequency
	0x10	20
	10x20	80
	20x30	200
	30x40	100

​

Refer to Exhibit 2-1. The percentage of students working between 10 and 20 hours is _____.

20%

The numbers of hours worked (per week) by 400 statistics students are shown below.

	Number of Hours	Frequency
	0x10	20
	10x20	80
	20x30	200
	30x40	100

​

Refer to Exhibit 2-1. The percentage of students working less than 20 hours is _____.

25%

The numbers of hours worked (per week) by 400 statistics students are shown below.

	Number of Hours	Frequency
	0x10	20
	10x20	80
	20x30	200
	30x40	100

​

Refer to Exhibit 2-1. The cumulative percent frequency for the class of 30 to 40 is _____.

100%

The numbers of hours worked (per week) by 400 statistics students are shown below.

	Number of Hours	Frequency
	0x10	20
	10x20	80
	20x30	200
	30x40	100

​

Refer to Exhibit 2-1. The cumulative frequency for the class of 20 to 30 is _____.

300

The numbers of hours worked (per week) by 400 statistics students are shown below.

	Number of Hours	Frequency
	0x10	20
	10x20	80
	20x30	200
	30x40	100

​

Refer to Exhibit 2-1. If a cumulative frequency distribution is developed for the above data, the last class will have a cumulative frequency of _____.

400

The numbers of hours worked (per week) by 400 statistics students are shown below.

	Number of Hours	Frequency
	0x10	20
	10x20	80
	20x30	200
	30x40	100

​

Refer to Exhibit 2-1. The percentage of students who work at least 10 hours per week is _____.

95%

The correlation coefficient ranges from which two values?

	0 and 1
	−1 and +1
	minus infinity and plus infinity
	1 and 100

-1 and +1

Let r be the correlation coefficient. If r = 0.5 for data set A and r = 0.8 for data set B, which of the following is true?

	The variables in B are more strongly correlated than the variables in A.
	The two data sets have the same level of correlation.
	The variables in A are more strongly correlated than the variables in B.
	None of the answers is correct.

the variables in B are more strongly correlated than the variables in A.

What would be the most appropriate way to measure the central location for the following data: 30, 25, 27, 31, 28, 29, 30, 27, 27, 1000. Hint: observe the extreme value in the data.

	mean
	range
	variance
	median

median

The variance of the exam grades for BE251-01 is 14, while the variance is 18 for BE251-02. Which class has more dispersed grades?

	None of the answers is correct.
	They are equally dispersed
	BE251-01
	BE251-02

BE251-02

The median of a sample will always equal the _____.

	mode
	mean
	50th percentile
	All of the answers are correct.

50th percentile

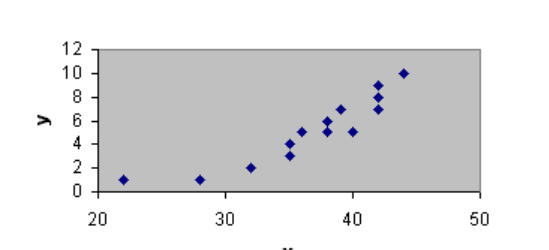
What relationship between x and y can you observe?

	A positive relationship
	A negative relationship
	No relationship
	None of the above

a positive relationshi

A researcher has collected the following sample data.

	5	12	6	8	5
	6	7	5	12	4

Refer to Exhibit 3-1. The 25th percentile is _____.

5

A researcher has collected the following sample data.

	5	12	6	8	5
	6	7	5	12	4

Refer to Exhibit 3-1. Suppose the 25th percentile is calculated to be 5. What does it mean?

25% percent of data

A researcher has collected the following sample data.

	5	12	6	8	5
	6	7	5	12	4

Refer to Exhibit 3-1. The median is _____.

6

A researcher has collected the following sample data.

5 12 6 8 5

6 7 5 12 4

Refer to Exhibit 3-1. The mode is _____.

5

A researcher has collected the following sample data.

	5	12	6	8	5
	6	7	5	12	4

Refer to Exhibit 3-1. The mean is _____.

7

A researcher has collected the following sample data.

	5	12	6	8	5
	6	7	5	12	4

Refer to Exhibit 3-1. The 1st quartile is _____.

5

A researcher has collected the following sample data.

3

5

12

3

2

Refer to Exhibit 3-2. The variance is _____.

16.5

A researcher has collected the following sample data.

3

5

12

3

2

Refer to Exhibit 3-2. The standard deviation is _____.

4.062

A researcher has collected the following sample data.

3

5

12

3

2

Refer to Exhibit 3-2. The range is _____.

10

A researcher has collected the following sample data.

3

5

12

3

2

Refer to Exhibit 3-2. The coefficient of variation is _____.

0.81

A numerical measure computed from a sample, such as sample mean, is known as a _____.

	population parameter
	sample parameter
	population statistic
	sample statistic

sample statistic

A numerical measure, such as a mean, computed from a population is known as a _____.

	population parameter
	sample parameter
	population statistic
	sample statistic

population parameter

The coefficient of variation is

	the same as the variance
	the standard deviation divided by the mean
	the square of the standard deviation
	the square root of the variance

the standard deviation deviation by the mean