Sampling distribution of the sample proportion

Sampling distribution of the sample proportion

Sampling distribution

• repeatedly taking a sample from a population

• calculating a statistic for every individual sample such as xbar

• combining that information on a graph to create a distribution (called sampling distribution)

Proportion

• describes the fraction of favourable outcomes, in relation to the whole

• This is what we are trying to study, e.g. someones height, age or score that they got on a test, etc = this is measured variables which we can record from a population or sample.

Example of a proportion

• proportion of people that have green eyes - we can measure this in two ways:

  1. take a sample and see how many people have green eyes within that sample

  2. we can interview the entire population and record how many people have green eyes

• sample size of 10, however only 2 people had green eyes: 2/10 = 0,2

• population size of 5000 and only 900 people had green eyes: 900/5000= 0,18

proportion of a sample is represented by

p hat: ˆp

proportion of a population is represented by

P

Formula of the proportion

number of favourable outcomes/ total number of outcomes

How to find: Sampling distribution of the sample population

• if we repeatdly take samples from the original population and calculate “p hat/ˆp” for each sample, we will get a lot of different data, & the possibilities are endless.

• the value of p hat/ˆp depends on the data which have been collected, & each sample can be different due to probability

• if we take all of these p hats/ ˆp, & put them onto a graph = distribution of p-hats/ ˆp = in other words this refers to the sampling distribution of the sample proportion.

Meaning of Sampling distribution of the sample population

• a distribution of the statistic ˆp, which was made from repeatedly taking random samples.

• like any distribution it will contain a value for the mean & a value for the standard deviation

The mean denoted of the sampling distribution of the sample proportion

µˆp = Mu p-hat

µˆp

The mean denoted of the sampling distribution of the sample proportion

The standard deviation denoted of the sampling distribution of the sample proportion

sigma p-hat

The standard deviation denoted of the sampling distribution of the sample proportion

In sample proportions, the standard deviation of the sample proportion is used to

• measure how much the sample proportion (𝑝̂) is likely to vary from the true population proportion (p).

Here’s the formula for the standard deviation (σₚ̂ ) of the sample proportion

What can we say about a sample proportion which is normal and follow a central limit theorem?

1. mu p-hat is equal to P \ this means that the average of all p-hats combined is equal to the population proportion P

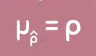
2. the standard deviation sigma p-hat is equal to the square root of PQ divided by n, where n is equal to the sample size, P is equal to the proportion of successful outcomes, & Q is equal to the proportion of outcomes that are not successful = because of this Q is equal to 1 minus P

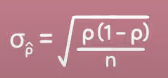
3. if it follows a mean of p, and a standard deviation of square root of p times 1 minus p/n - then we can use the score table and the standardization formula to help us calculate areas related to certain Z-scores

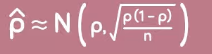
Central limit theorem is different

• in sampling distribution of the sample mean x-bar, the central limit theorem applies when the sample size n is greater than or equal to 30

  

• in sampling distribution of the sample proportion = it has to satisfy two conditions: n*p must be greater or equal to 10, & second condition is that n*1-p must be greater than or equal to 10

if this is done, the central limit theorem can be applied, & also the z-score table can be used by using the appropriate standarization formula.

Relation to sampling distribution of the sample proportion

• binomial distribution

• probability