CLASS 1 - COVARIANCE AND SCATTERPLOTS

STATS II

Variance:

how much do observations deviate from the central tendency? 

How spread out are the variables? More spread out = more variance. 

Sum up all the mean, square so it’s positive then subtract the number of observations minus one. 

Covariance:

 How much do variables vary together? How much do those circles overlap?

Sum up all the mean, square so it’s positive (now we look at both observations together) then subtract the number of observations minus one. 

FOCUS: If one variable increases or decreases, how does it affect the outcome? (-,+)

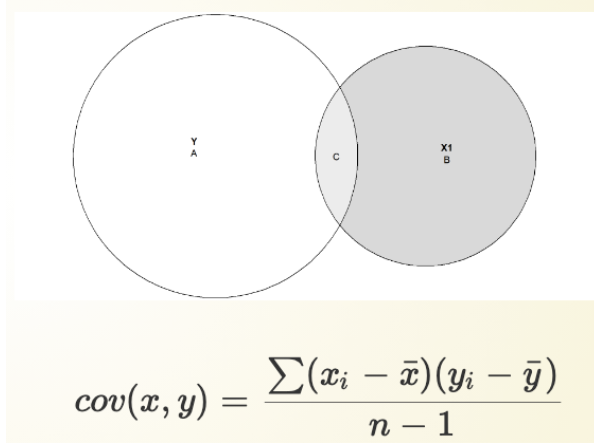
Looking for Covariance in a Scatterplot

Scatterplots: Visual inspection (for two continuous variables)

x-axis = IV

y-axis = DV

<= Negative Association (data clusters in the upper left and bottom right quadrants). 

To better analyze the relationship => Divide the figure into quadrants (determined by means), it is easier to see prevalence then.

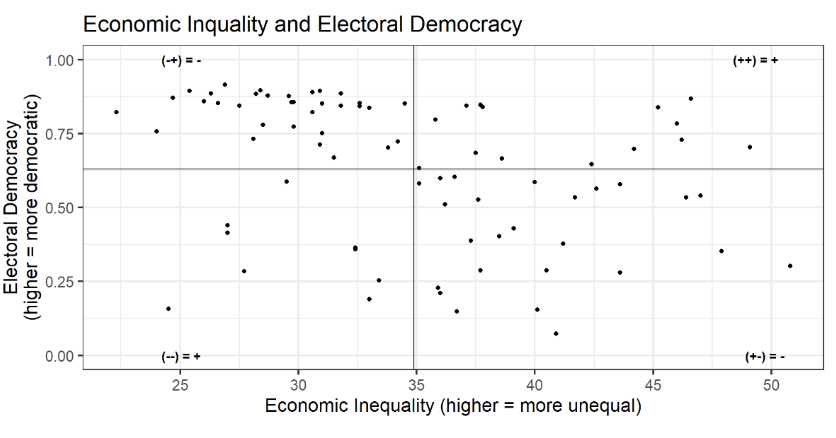
Covariance: Calculation 

Covariance Statistic: Summary statistic of relationship 

<= Negative covariance (Note, probably calculations not on the exam)

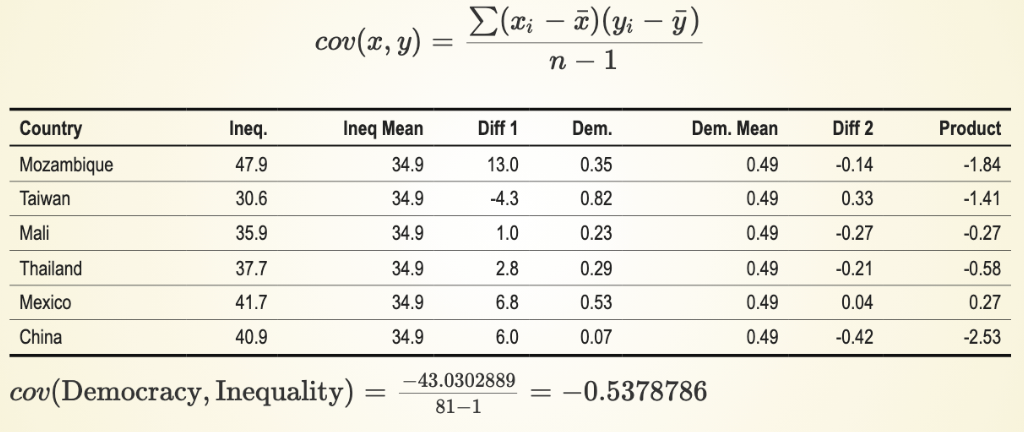
Covariance: Scale

Scale matters

<= The denominator is the same (the number of observations on both are the same), in both cases DV is the same, but with different IVs.

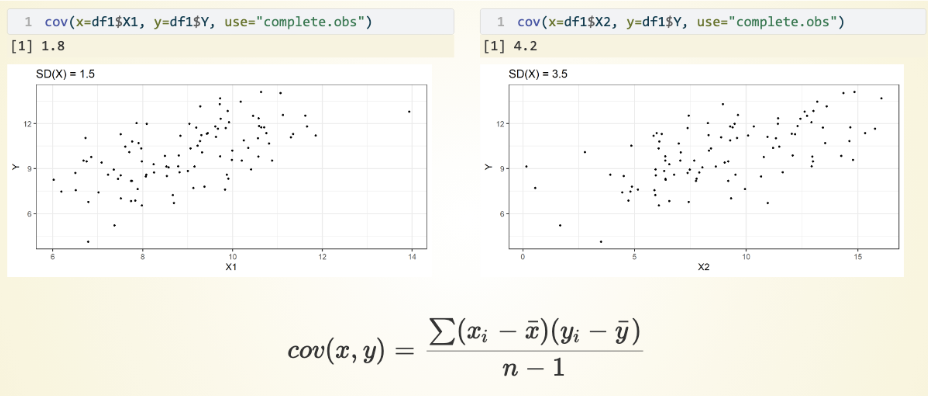
Are covariance statistics standardized or unstandardized?

Covariance statistics are unstandardized. 

Are correlation statistics standardized or unstandardized?

Correlation coefficients = standardized covariance statistic.

Are linear regression models standardized or unstandardized?

Linear regression models are not standardized but with many other advantages.  

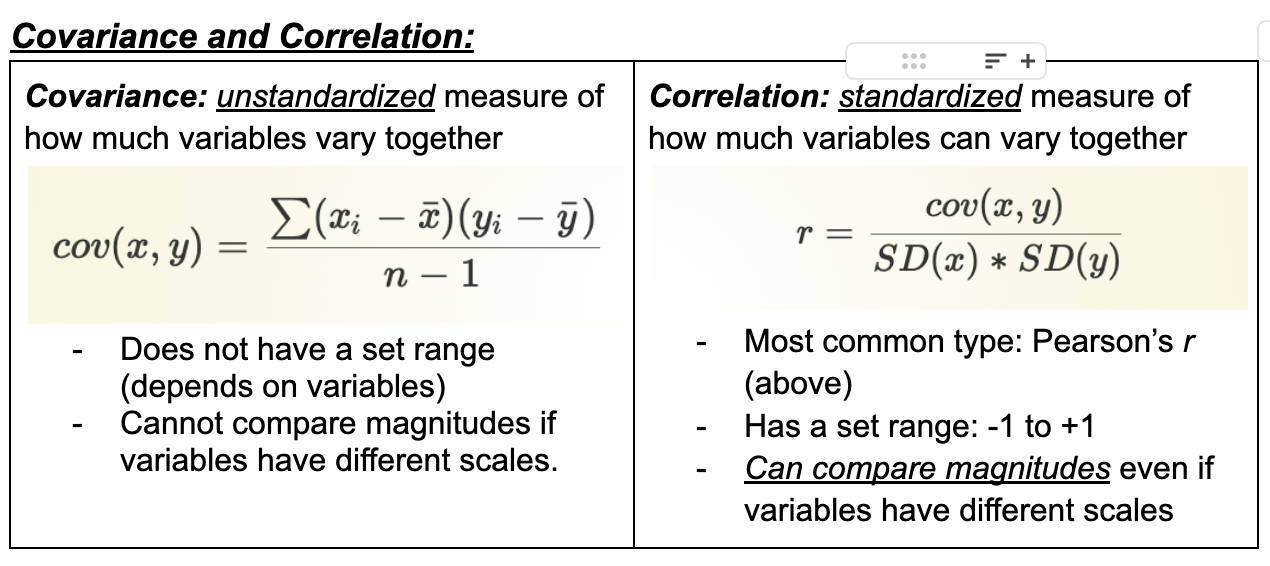
Covariance

unstandardized measure of how much variables vary together

• Does not have a set range (depends on variables)

• Cannot compare magnitudes if variables have different scales.

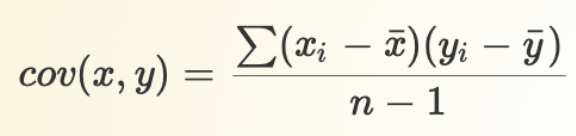
Correlation

standardized measure of how much variables can vary together

• Most common type: Pearson’s r (above)

• Has a set range: -1 to +1

Can compare magnitudes, even if variables have different scales

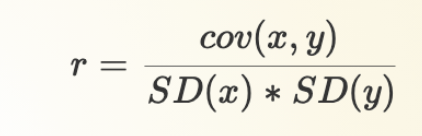
Correlation vs Covariance

Correlation: Basic Interpretation

Correlation statistics range from -1 to +1

• Positive values

  • As one variable increases, so does the other one

  • +1 = perfect positive linear relationship 

    • Positive relationship (= as one variable increases the other does as well)

      • +1 = all of our points in a scatterplot fall in a perfectly sloped straight upwards line.

• Negative Values 

  • As one variable increases, the other decreases

  • - 1= perfect negative linear relationship 

  • Negative relationship (= as one variable increases the other decreases)

    • - 1 = all of our points in a scatterplot fall in a perfectly sloped straight downwards line.

• 0 value: No linear relationship

Correlation: “Size” Rule of Thumb

Correlations range from -1 to +1 

• -1: Perfect negative linear relationship between variables

• 0: No linear relationship between variables

• +1: Perfect positive linear relationship variables

One common rule of thumb for interpreting correlation effect sizes:

• r < |0.1|: Very small

• |0.1| <= |0.3|: Small

• |0.3| <= |0.5|: Moderate

• r > |0.5|: Large

P-Value

P-value: Assuming that the correlation between the two variables in the population was 0, what is the probability of finding a t-statistic of this size (|3.12|) or greater?

Conventional threshold for “significance”: p < 0.05

Reporting and interpretation  - Economic Inequality and Electoral Democracy

Interpretation: Higher levels of economic inequality are associated with lower levels of electoral democracy (r = -0.33). This association is moderate in size and statistically significant (p < 0.01).

Caution: Correlation

A correlation coefficient (unless -1 or +1) could hide a variety of different patterns. 

<= every plot shows zero correlation (but do not reflect NO relationship ONLY that there is NO LINEAR relationship). 

• There are relationships with different kinds of correlation. 
  

Model = simplification of reality (can give wrong answers, must learn how to interpret).

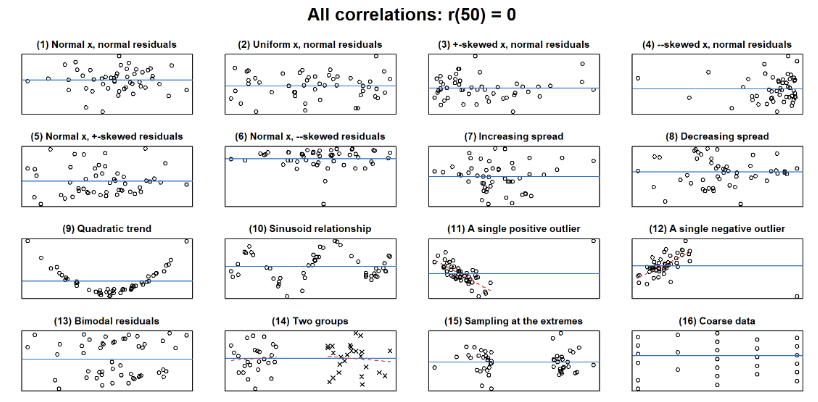
Assumptions of Pearson’s r

• Interval-ratio (“continuous”) variables

• A linear relationship between variables < = Assumption can be wrong!

Spearman’s rho

• Primarily used for discrete ordinal variables and when assumptions of Pearson’s are violated (e.g., no linear relationship)

  • Data is ordinal or the relationship is not strictly linear

• Measures the strength and direction of association between two ranked variables

  • Looking at the association between the ranks of two variables in the distribution

May also see Kendall’s tau-b when there are many ties

Quick Review: Correlations

• Correlation Coefficient: a standardized measure of the linear association between two continuous variables

• Ranges from -1 to +1: values closer to -1/+1 = stronger associations

• Non-linear relations and/or ordinal data? Use Spearman’s rho

• Correlation ≠ Causation

Linear Regression

Correlation: How closely do points cluster around a straight line?

Linear Regression:What are the properties of that straight line?

Linear Regression: Definition: Linear regression is “a method that allows researchers to summarize how predictions or average values of an outcome vary across [observations] defined by a set of predictors.”

Why Two Methods? 

When both variables are continuous: provide different (but related) information

• Both tell us about the direction of the relationship 

• Correlation is easier to use when assessing effect size (correlation = standardized effect size). 

• Linear regression allows to assessment of standardized effect size, more specific predictions, and causality

DV and IV

Prediction

Goal = What is our best guess about one variable if we know what the other variable(s) equals?

Goal = to guess, or best predict one variable based on another.

Example: what is our best guess about the level of democracy in a country if we know its level of inequality?

Predicting one variable with Another

• Prediction with access to just Y: average value of Y

• Prediction with another variable: for any value of X, what’s the best guess

• of Y?

  • Example: What’s my best guess about the country’s level of democracy if the Gini coefficient = 30?

• We need a function (y=f(x)) that maps values of X into predictions

  • Machine learning = fancy ways to determine the function.

Using a Line to Predict

• Can we smooth these binned means and close gaps? Yes, via a model!

• Models: abstractions that may be useful for answering our questions

  • We make some simplifying assumptions to generate predictions. 

• Simplest model: a straight line

All we need to know in order to make a prediction: the value of X, the intercept of the line, and its slope: y = ax + b

Sample Regression Equation 

• The equation here refers to the “line of best fit” or “best fitting” line within a sample of observations. 

  • Regression line = straight line

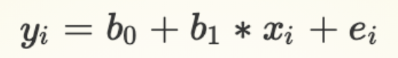
Subscript i 

Subscript i refers to different observations in our mode

• y_i = Value of y for observation i = {1,2,3...}

• x_i = Value of x for observation i = {1,2,3...}

• e_i = Value of for observation i = {1,2,3...}

y₂₅ = b₀ + b₁* x₂₅: What is the predicted value for observation 25?

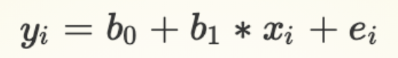
Parameters / Coefficients

Coefficients/Parameters: b₀ ,b₁

• b₀: Intercept of the line of best fit (also referred to as the Constant term)

• b₁: Slope of the line of best fit

Multiple linear regression models will have multiple slope terms/coefficients: b₂,b₃ …

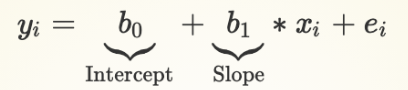
Intercept - Regression Equation

b₀: intercept

• Average value of Y we expect to observe when X = 0

• Average value of V-Dem democracy score measure we expect to observe when the inequality measure = 0

  • The expected average value of a country with perfect equality

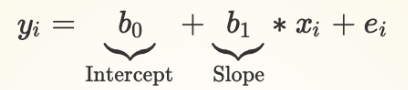
Slope Coefficient - Regression Equation

b₁: Slope of line (Slope term; coefficient for IV)

• How we expect the mean of Y to change when X increases by one unit

  • When x changes given how Y changes (rise/run)

• How we expect the mean V-Dem democracy score to change when our inequality measure goes from 0 to 1, or 1 to 2, or 10 to 11...

• Assumption: same amount of expected change in Y for each one unit change in X (Week 4)

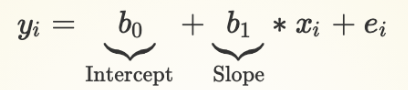
Populations vs Sample

Population: Observations of relevance for our RQ

Sample: Selection of observations we actually analyze

Coefficients: Sample and Population

• Our goal is to understand what b₀ and b₁ are in the population

• We use estimates of them in our sample to infer what they are likely to be in the population

  • An estimate is our best guess about some parameter

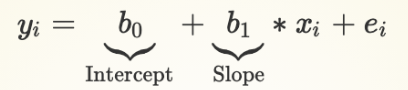
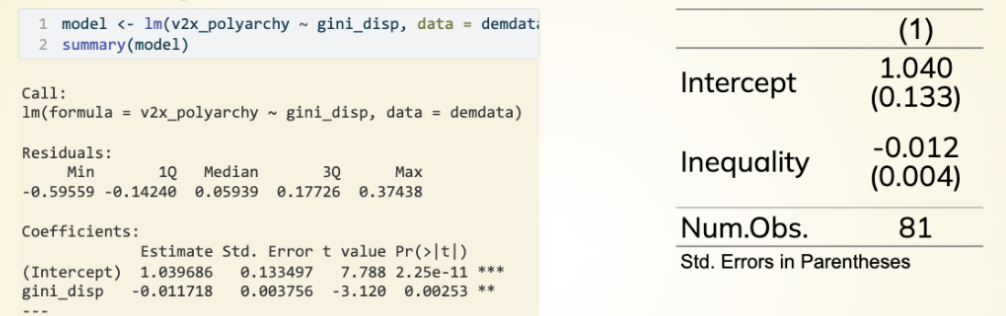
Our Example - What do columns mean?

• “Estimate” = Coefficient (Intercept or Slope)

• “Std. Error” = Standard Error of coefficient (next week!)

• “Num.Obs” = # Observations in mode

• What is the mean value we expect to observe when our IV = 0?

  • ...What if X doesn’t/cannot equal 0?

What do we do if IV cannot Equal Zero?

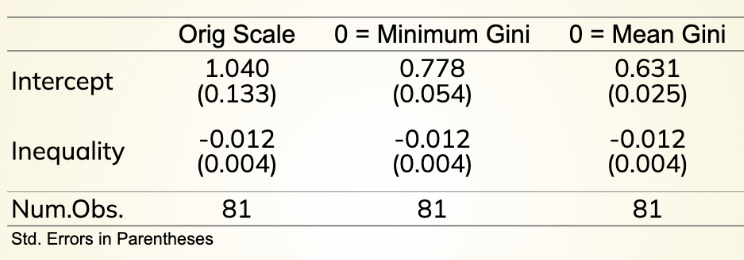
Intercept = Mean value we expect to observe when IV = 0 

< = If cannot = 0 (not actually possible), rescale the IV

Orig scale = In a perfect world we would expect 0 inequality and a democracy score of 1.040

Minimum Gini = Found inequality variable and subtracted the minimum from it  

Mean Gini = Found inequality variable and subtracted the mean from each observation. 

^ Intercepts change because you change what zero means in each context of the regression. 

• Changing Y but not the slope (inequality remains the same). 

Slope Term /Coefficient

• How should we expect the mean of Y to change if X increases by 1 unit?

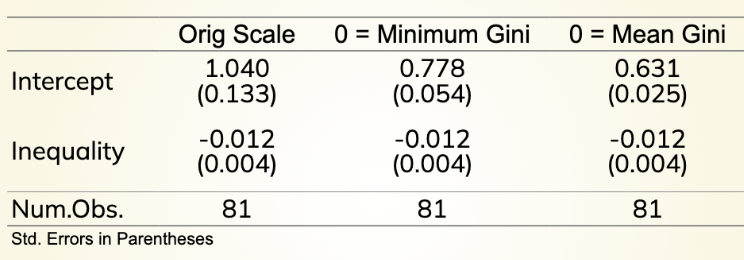
Reporting/Interpretation of Slope (IV: Democratic scores; DV: Inequality)

Higher levels of economic inequality are associated with lower levels of electoral democracy. We expect that democracy scores will decrease by 0.012 scale points, on average, with each one-unit increase in inequality.

^ incremental change (per one unit increase). 

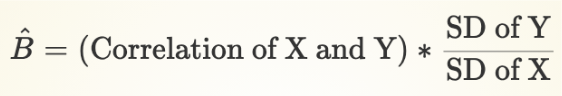
Slope Coefficient and Correlation Coefficient

The slope coefficient is related to the correlation coefficient

• Correlation = -0.33

• SD of X = 6.78

• SD of Y = 0.25

• Coefficient = -0.012

• Is this a “big” or “small” relationship?

  • It's 0.012 and unstandardized

  • Difficult to assess because changes are incremental

• Regression coefficients are unstandardized so it’s difficult to say

• A way to start: use the model to calculate predicted or expected values of

• Y at different values of X and use knowledge about the topic to advance a claim about the importance

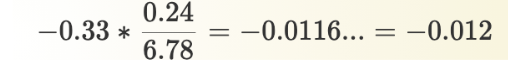
Review

Three related ways for investigating the relationship between a continuous DV and a continuous IV:

• Covariance: Unstandardized measure of the association between two continuous measures

• Correlation: Standardized measure of the association between two continuous measures

• Linear Regression: Prediction line telling us how to expect the mean of Y to change when X changes by 1 unit