AP Calculus BC - Polar Equations
0.0(0)
0.0(0)
Card Sorting
1/52
Earn XP
Description and Tags
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
53 Terms
1
New cards
√x^2 + y^2
(Cartesian to polar) r =
2
New cards
arctan y/x
(Cartesian to polar) θ =
3
New cards
r cos θ
(Polar to cartesian) x =
4
New cards
r sin θ
(Polar to cartesian) y =
5
New cards
Circles, Roses, lines, and limaçons
Types of polar equations
6
New cards
r = a
r = a sin θ
r = a cos θ
r = a sin θ
r = a cos θ
Equations of circles
7
New cards
The x-axis
A polar equation that has cos θ has symmetry with...
8
New cards
The y-axis
A polar equation that has sin θ has symmetry with...
9
New cards
The length of the diameter
In a circle equation (excluding r = a), a is...
10
New cards
The location of the circle in the polar plane
In a circle equation (excluding r = a), the sign of a determines:
11
New cards
0 ≤ θ ≤ 2π
Range of θ for r = a
12
New cards
0 ≤ θ ≤ π
Range of θ for r = a sin θ & r = a cos θ
13
New cards
r = a sin nθ
r = a cos nθ
r = a cos nθ
Types of rose equations:
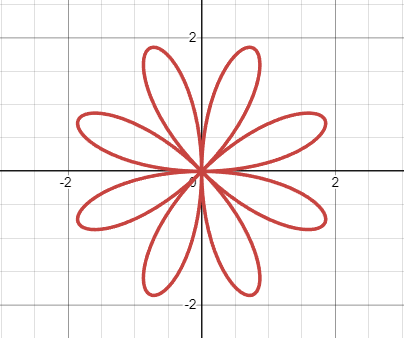
14
New cards
The length of the petals
In a rose equation (r = a sin nθ & r = a cos nθ), a is equal to:
15
New cards
The number of petals the graph will have
In a rose equation (r = a sin nθ & r = a cos nθ), if n is odd, then n is equal to:
16
New cards
n times 2 is equal the number of petals the rose will have (2n).
In a rose equation (r = a sin nθ & r = a cos nθ), if n is even, then n is equal to:
17
New cards
0 ≤ θ ≤ 2π
Range of rose equations (r = a sin nθ & r = a cos nθ):
18
New cards
r = a ± b sin θ
r = a ± b cos θ
r = a ± b cos θ
Equations of limaçons:
19
New cards
Cardiods, Iner Loops, and Beans
Types of limaçons:
20
New cards
0 ≤ θ ≤ 2π
Ranges of limaçons:
21
New cards
Where the graph is located
In a limaçon, the sign of b determines:
22
New cards
heart
A cardiod graph roughly has the shape of a
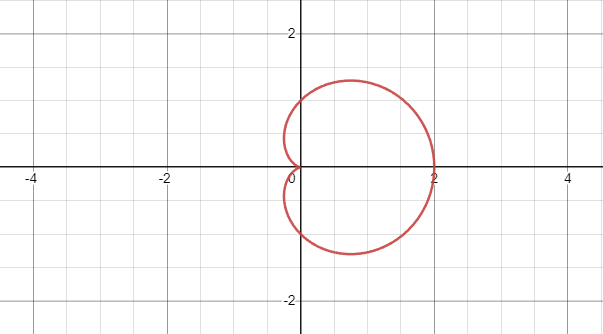
23
New cards
a = b
For a limaçon to be a cardiod, what is the relationship between a & b:
24
New cards
The length from the origin to the intercepts it has with either axis (the axis which is being intercepted depends on wether it is cos θ or sin θ)
In a cardiod, a is equal to:
25
New cards
The point from the origin to the max length
In a cardiod, a + b determines:
26
New cards
Where most of the graph is located.
In a cardiod, the sign of b determines:
27
New cards
0
In a cardiod, b-a is equal to:
28
New cards
It has an inner loop that then loops around and connects to make a bigger shape
What does an inner loop graph look like?
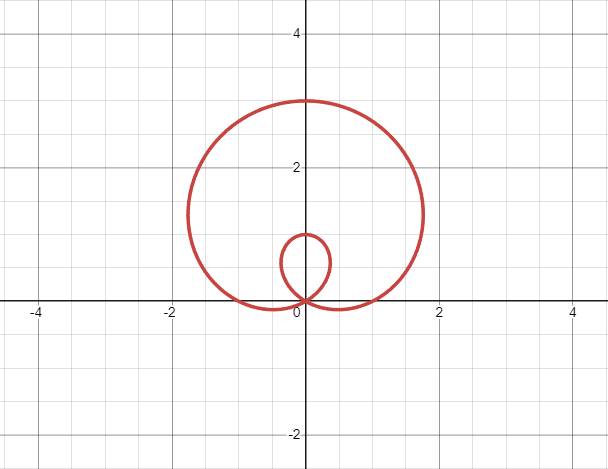
29
New cards
a < b
For a limaçon to be an inner loop, what is the relationship between a & b:
30
New cards
The length of the intercepts the graph will have
In an inner loop, what does the value of a determine?
31
New cards
Where most of the graph will be located in
In an inner loop, what does the sign of b determine?
32
New cards
The vertex of the inner loop
In an inner loop, what does b-a determine?
33
New cards
The vertex of the big shape
In an innner loop, what does b+a determine?
34
New cards
Like a bean
What does the graph of a bean limaçon look like?
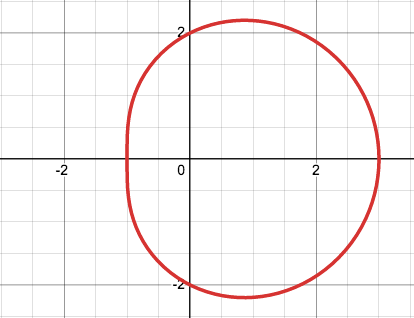
35
New cards
a > b
For a limaçon to be a bean, what is the relationship between a & b:
36
New cards
The length the short vertext
In a bean, what does a determine?
37
New cards
Where most of the graph will be
In a bean, what does the sign of b determine?
38
New cards
The length of the main long vertext
In a bean, what does the value of a+b determine?
39
New cards
The length of the main short vertext
In a bean, what does the vale of b-a determine?
40
New cards
A line
What does a line graph look like?
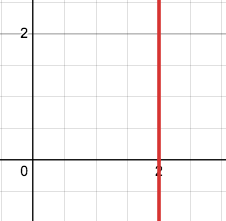
41
New cards
r = a sec θ
r = a csc θ
r = a csc θ
What are the equation for line graphs?
42
New cards
Vertical line at the value of a
r = a sec θ is a
43
New cards
Horizontal line at the value of a
r = a csc θ is a
44
New cards
Trig Idenitity: cos^2 θ=
1/2(1+ cos 2θ)
45
New cards
Trig Idenitity: sin^2 θ=
1/2(1-cos 2θ)
46
New cards
At what values does a polar equation have horizontal tangent lines?
When dy/dθ = 0 and dx/dθ ≠ 0
47
New cards
How can we find a horizontal tangent line?
We must find values that make dy/dθ = 0 and then substitute them into dx/dθ to ensure that dx/dθ ≠ 0 at that value.
48
New cards
At what values does a polar equation have vertical tangent lines?
When dx/dθ = 0 and dy/dθ ≠ 0
49
New cards
How can we find a vertical tangent line?
We must find values that make dx/dθ = 0 and then substitute them into dx/dθ to ensure that dy/dθ ≠ 0 at that value.
50
New cards
What is dy/dx in a Polar Equation?
dy/dθ / dx/dθ
51
New cards
What is dy/dθ / dx/dθ?
r cos θ + r' sin θ
-------------------------------
r(-sin θ) + r' (cos θ)
-------------------------------
r(-sin θ) + r' (cos θ)
52
New cards
What is dy/dθ ?
r cos θ + r' sin θ
53
New cards
What is dx/dθ ?
r(-sin θ) + r' (cos θ)