Exam 2: Absolute Value Functions, Quadratic Functions, and Polynomials

Defining the absolute value function as a piecewise function

If x is negative, the absolute value of x can be represented by the "opposite of x" (written -x). If x is greater than or equal to 0, the absolute value of x can be represented as just x.

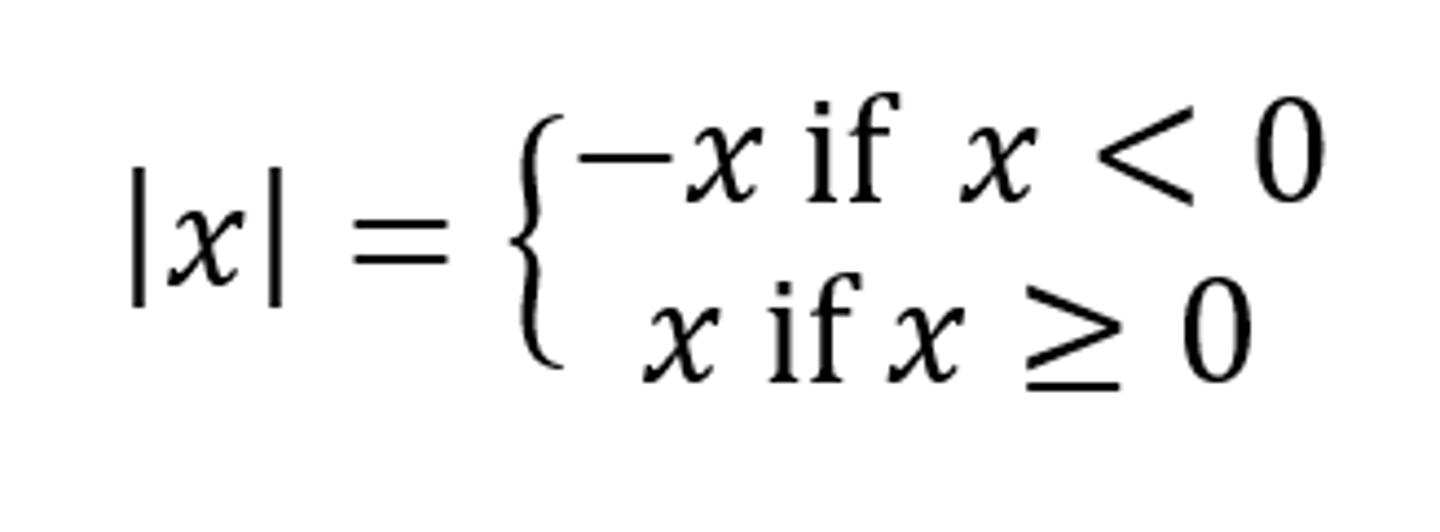
|x| = 0 if and only if ___________________________.

x = 0

For c>0 (meaning positive!), |x| = c if and only if ____________________________.

x = c or x = -c

For c<0 (meaning negative!), |x| = c has _______________________________.

no solution

What are the steps for solving a "simple" absolute value equation with no other x-terms outside of the absolute value?

1. Get the equation in the form absolute value equals some number

2. Use the sign of the number on the righthand side to determine which case of the "Equality Properties for Absolute Value" you have.

3. Solve any equation(s) you get from applying the "Equality Properties for Absolute Value".

What are the steps for solving an absolute value equation that cannot be expressed in the form absolute value equals some number?

1. Write the absolute value parts as piecewise functions.

2. Break up the equation into cases, by using each piece of the piecewise function individually.

3. Solve the equations corresponding to each piece.

4. Check for extraneous solutions!!

What is the general form for a quadratic function?

f(x)=ax²+bx+c

What is the standard form for a quadratic function?

f(x)=a(x-h)²+k

For a quadratic function given in the standard form f(x)=a(x-h)²+k, identify the vertex and the axis of symmetry.

vertex: the point (h,k)

axis of symmetry: the vertical line x=h

What is the domain of a polynomial function?

(-∞,∞)

What are the 4 ways to solve a quadratic equation for x?

1. Factor and use the zero product property

2. Complete the square

3. Use the "Square Root Property"

4. Use the quadratic formula

What are the steps to get a quadratic function from general form [f(x)=ax²+bx+c] into standard form [f(x)=a(x-h)²+k]?

Complete the Square:

1. Factor out the number a from the x² and x terms.

2. Take half of the new coefficient of x and square that quantity.

3. Add a form of zero, by adding the result from step 2 inside the parentheses and the subtracting that total value outside of the parentheses.

4. Factor the inside of the parentheses into a perfect square and combine constant terms.

The Quadratic Formula

Solves equations of the form ax²+bx+c=0 where

"x equals the opposite of b plus or minus the square root of b squared minus 4ac all over 2a"

The Discriminant

The inside of the square root part of the Quadratic Formula: b²-4ac

3 Different Cases Based on the Sign of the Discriminant

1. If the discriminant is negative, then the equation ax²+bx+c=0 has no real zeros.

2. If the discriminant is zero, then the equation ax²+bx+c=0 has 1 real zero.

3. If the discriminant is positive, then the equation ax²+bx+c=0 has 2 real zeros

the imaginary unit, i

Satisfies two properties:

1. i ² = -1

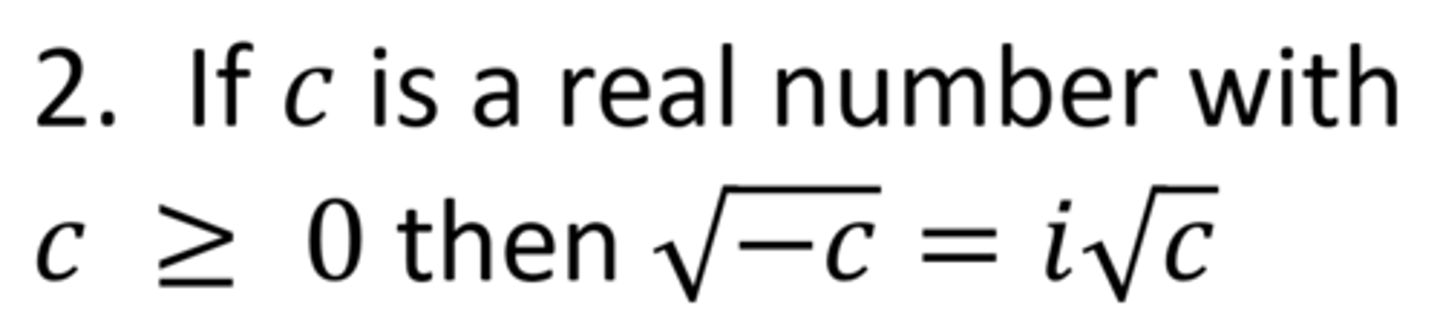
4 Different Types of Solutions Based on the Discriminant

1. If the discriminant is negative, then the equation ax²+bx+c=0 has two complex zeros.

2. If the discriminant is zero, then the equation ax²+bx+c=0 has one rational zero.

3. If the discriminant is positive and a perfect square, then the equation ax²+bx+c=0 has two rational zeros

4. If the discriminant is positive and a not perfect square, then the equation ax²+bx+c=0 has two irrational zeros

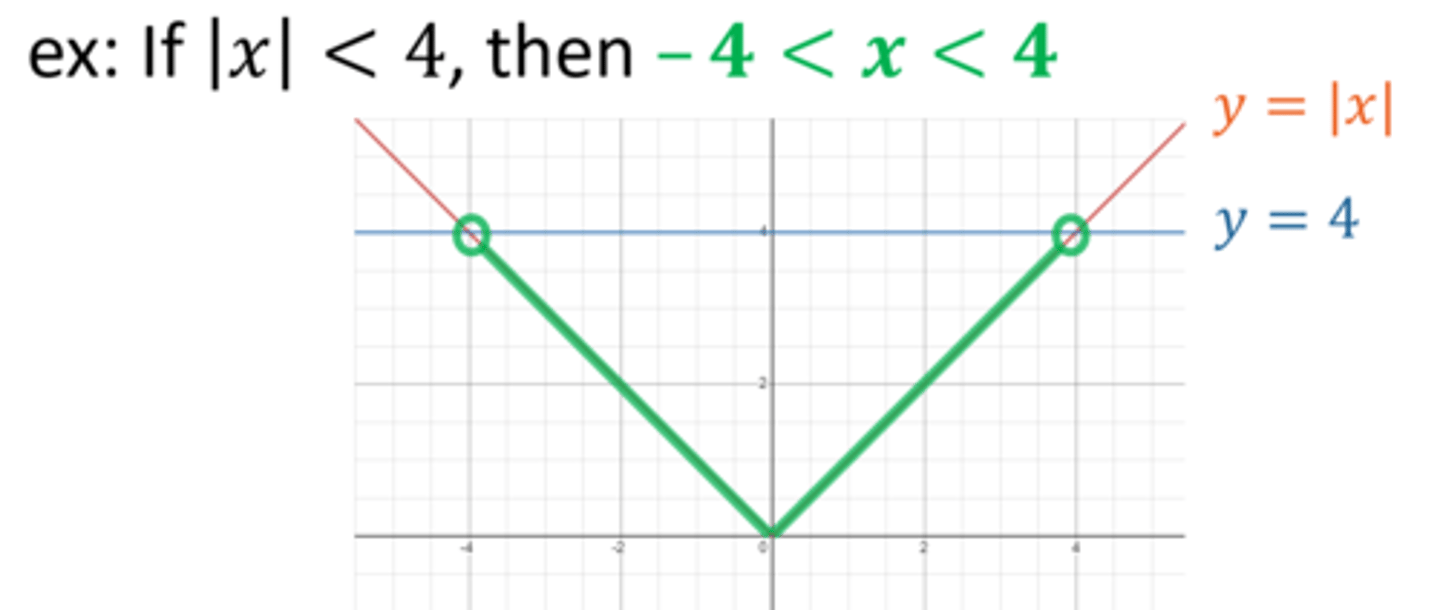
Complete the "Theorem: Inequalities Involving the Absolute Value"

Let c be a real number.

For c > 0, |x| < c is equivalent to __________________________ .

-c < x < c

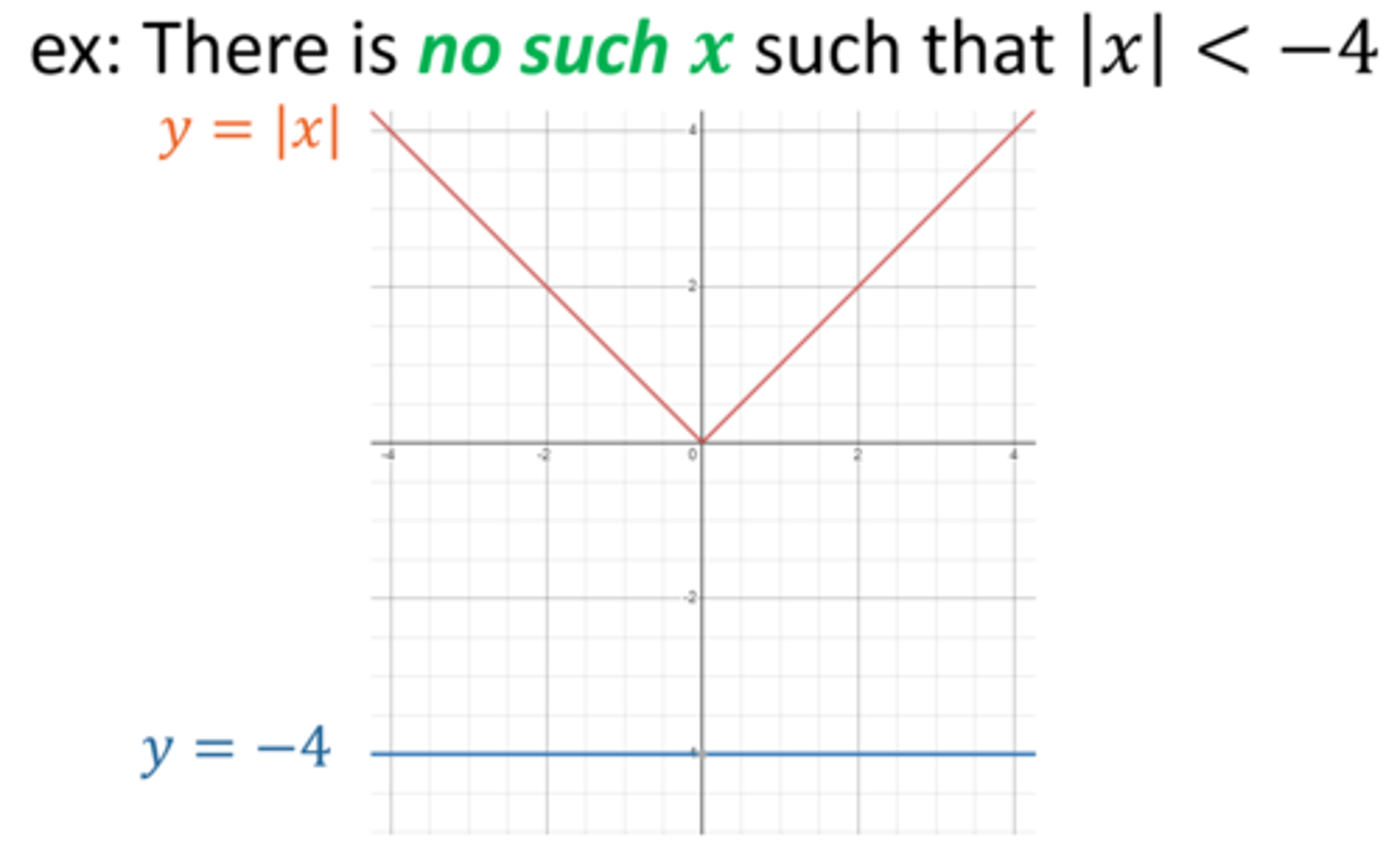
Complete the "Theorem: Inequalities Involving the Absolute Value"

Let c be a real number.

For c ≤ 0, |x| < c is equivalent to __________________________ .

no solution

Complete the "Theorem: Inequalities Involving the Absolute Value"

Let c be a real number.

For c ≥ 0, |x| > c is equivalent to __________________________ .

x < -c or x > c

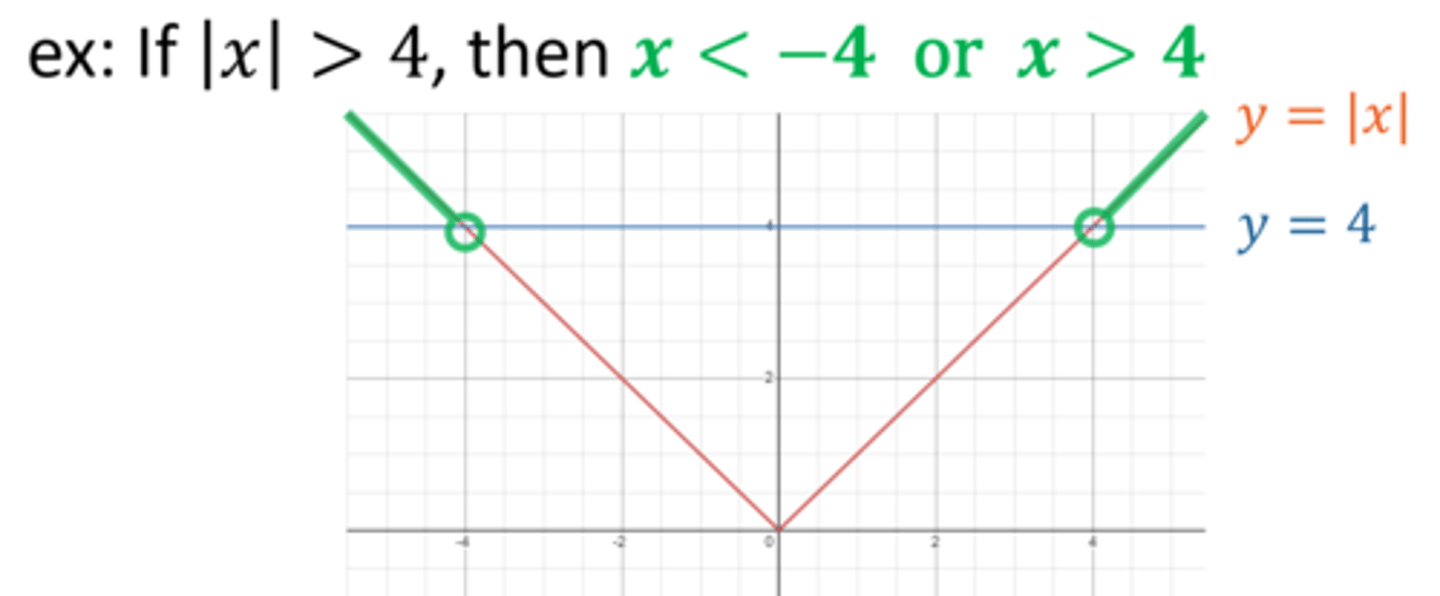
Complete the "Theorem: Inequalities Involving the Absolute Value"

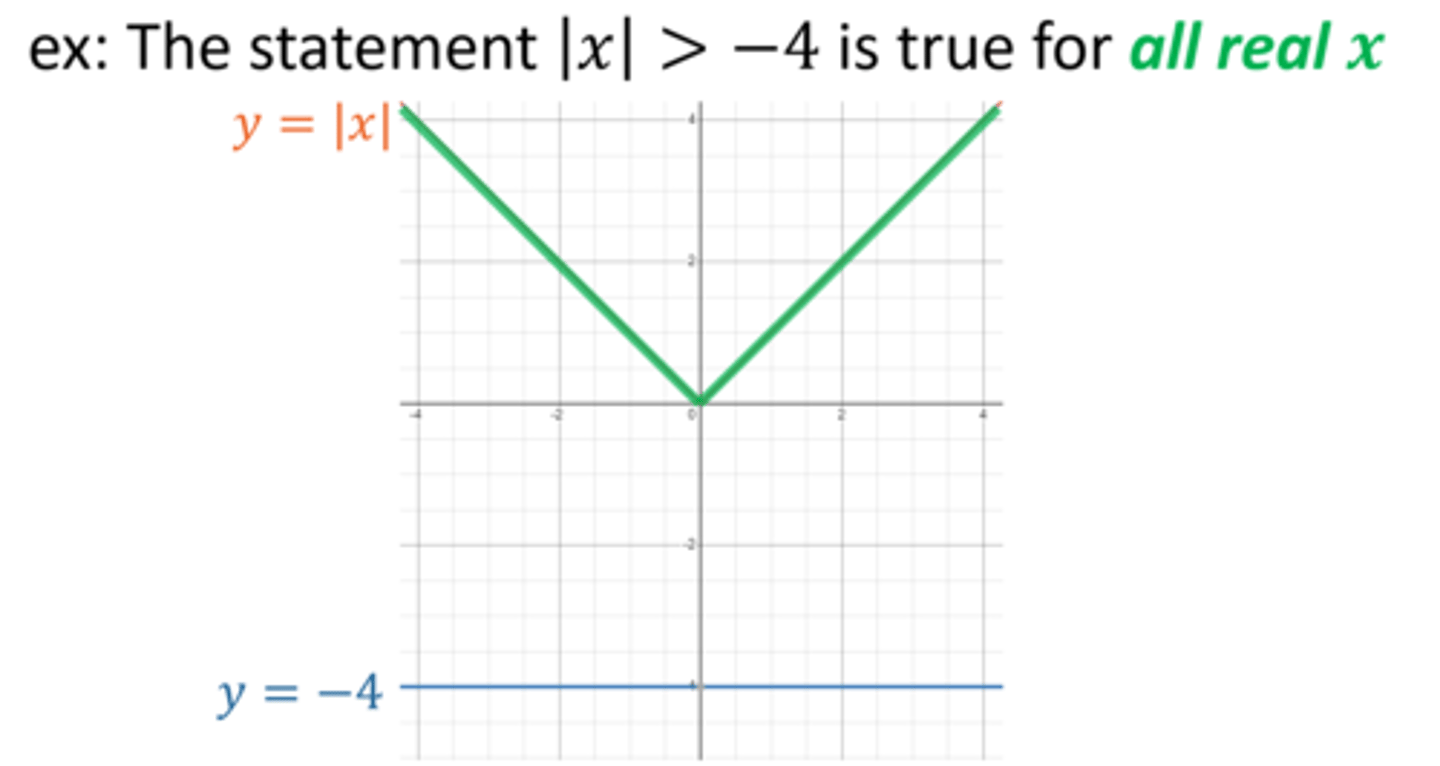
Let c be a real number.

For c < 0, |x| > c is equivalent to __________________________ .

all real numbers

What are the steps for solving a "simple" absolute value inequality [with no other x-terms outside of the absolute value]?

1. Isolate the absolute value on one side of the inequality with a number on the other side.

2. Determine which of the 4 structures of our "Theorem: Inequalities Involving the Absolute Value" your problem resembles.

3. Use the result from the Theorem to rewrite the inequality as an equivalent inequality [or inequalities] that does not have an absolute value.

4. Solve.

5. Draw the solution intervals on a number line to help you state the answer in interval notation.

What are the steps for using a sign diagram to solve a quadratic inequality?

1.Rewrite the inequality, if necessary, as a quadratic function f(x) on one side of the inequality and 0 on the other.

2.Find the zeros of f and place them on the number line with the number 0 above them.

3.Choose a real number, called a test value, in each of the intervals determined in step 2

4.Determine the sign of f(x) for each test value in step 3, and write that sign above the corresponding interval.

5.Choose the intervals which correspond to the correct sign to solve the inequality.

A Polynomial

A function with the pictured form:

where the coefficients are real numbers and

n>=1 is a natural number, {1, 2, 3, ...}.

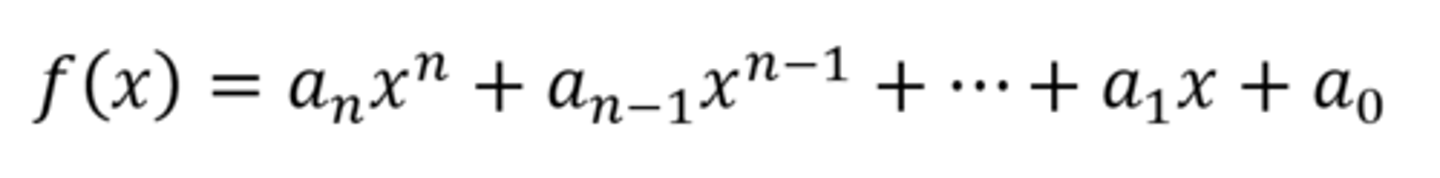
The Degree of a Polynomial

The largest power on x when the polynomial is expressed in its general/expanded form.

The Leading Term of a Polynomial

The term corresponding to the largest power on x when the polynomial is expressed in its general/expanded form.

The Leading Coefficient of a Polynomial

The number by which xⁿ is multiplied in the leading term

The Constant Term of a Polynomial

The term that has no variable when the polynomial is expressed in its general/expanded form.

What are the characteristics of a polynomial graph?

Polynomials are smooth, continuous, and have infinite end behavior.

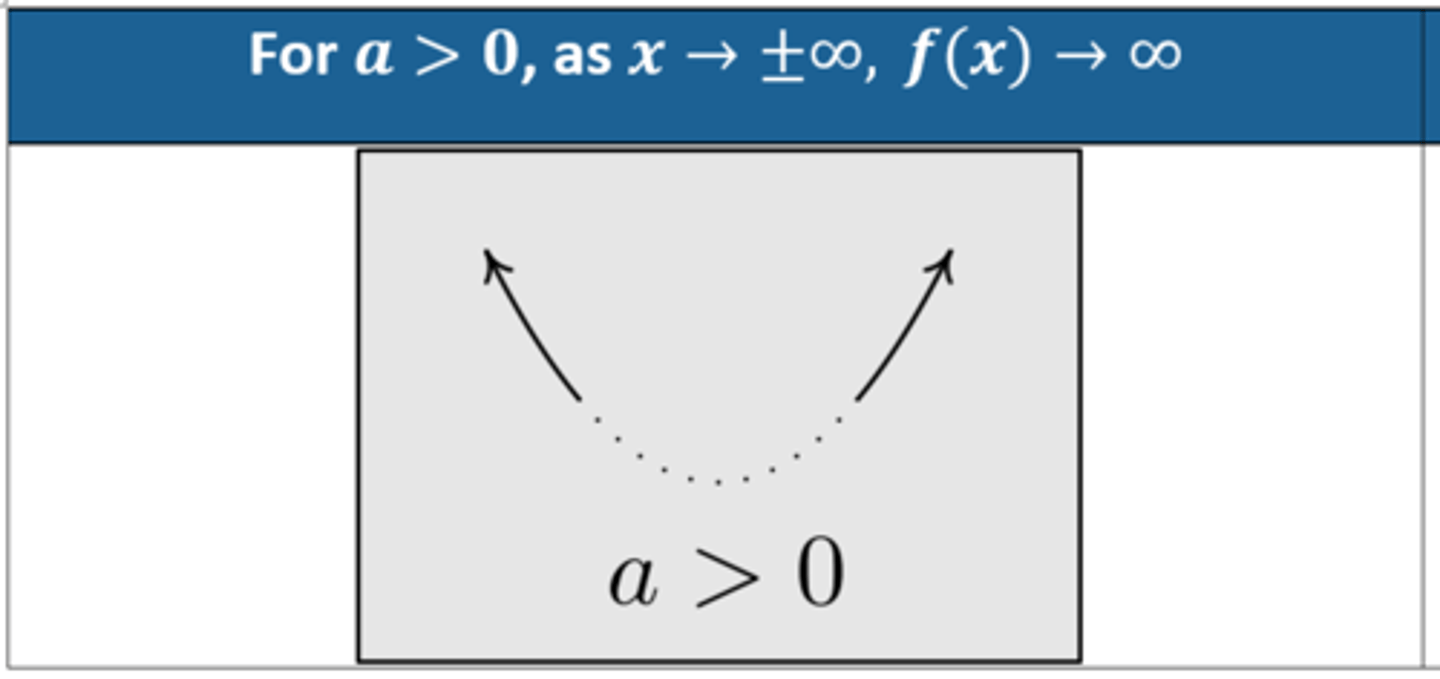
What is the end behavior for the function f(x)=axⁿ, when n is even and a is positive?

As x→±∞, f(x)→∞

What is the end behavior for the function f(x)=axⁿ, when n is even and a is negative?

As x→±∞, f(x)→-∞

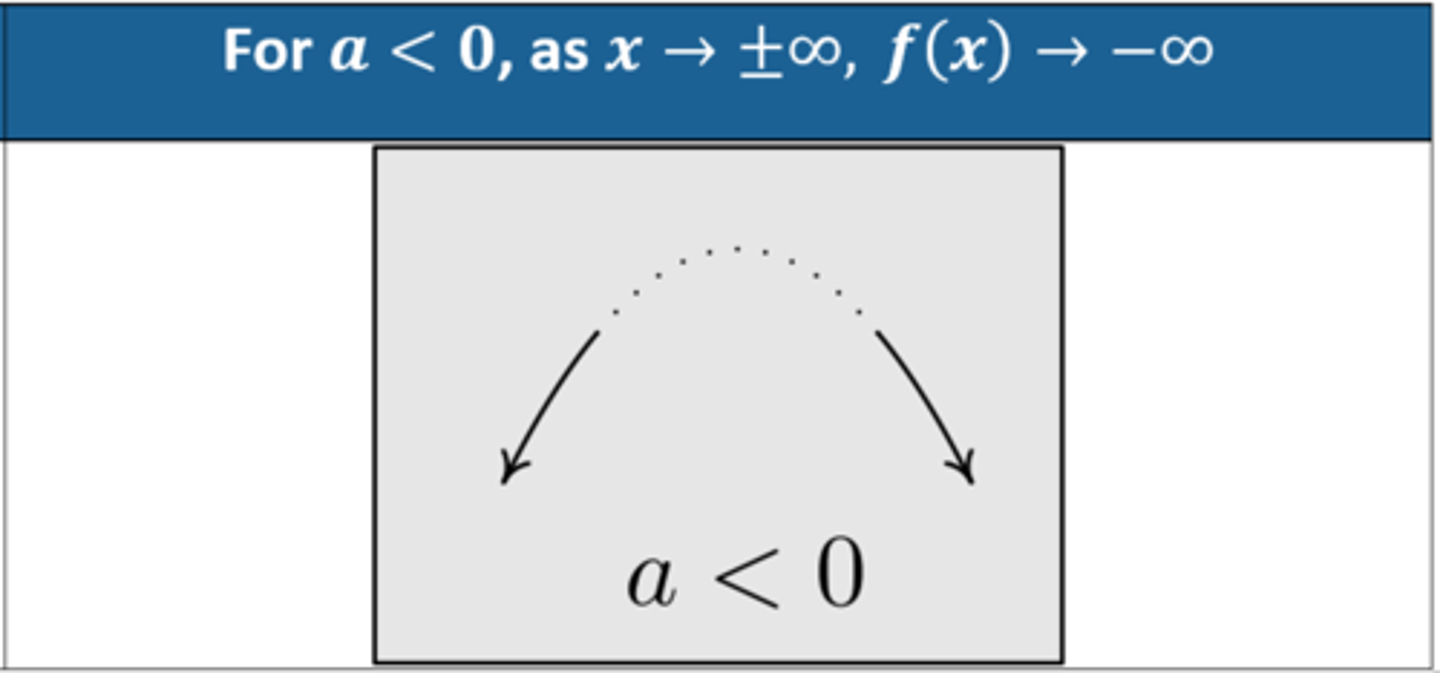
What is the end behavior for the function f(x)=axⁿ, when n is odd and a is positive?

As x→-∞, f(x)→-∞ and as x→∞, f(x)→∞

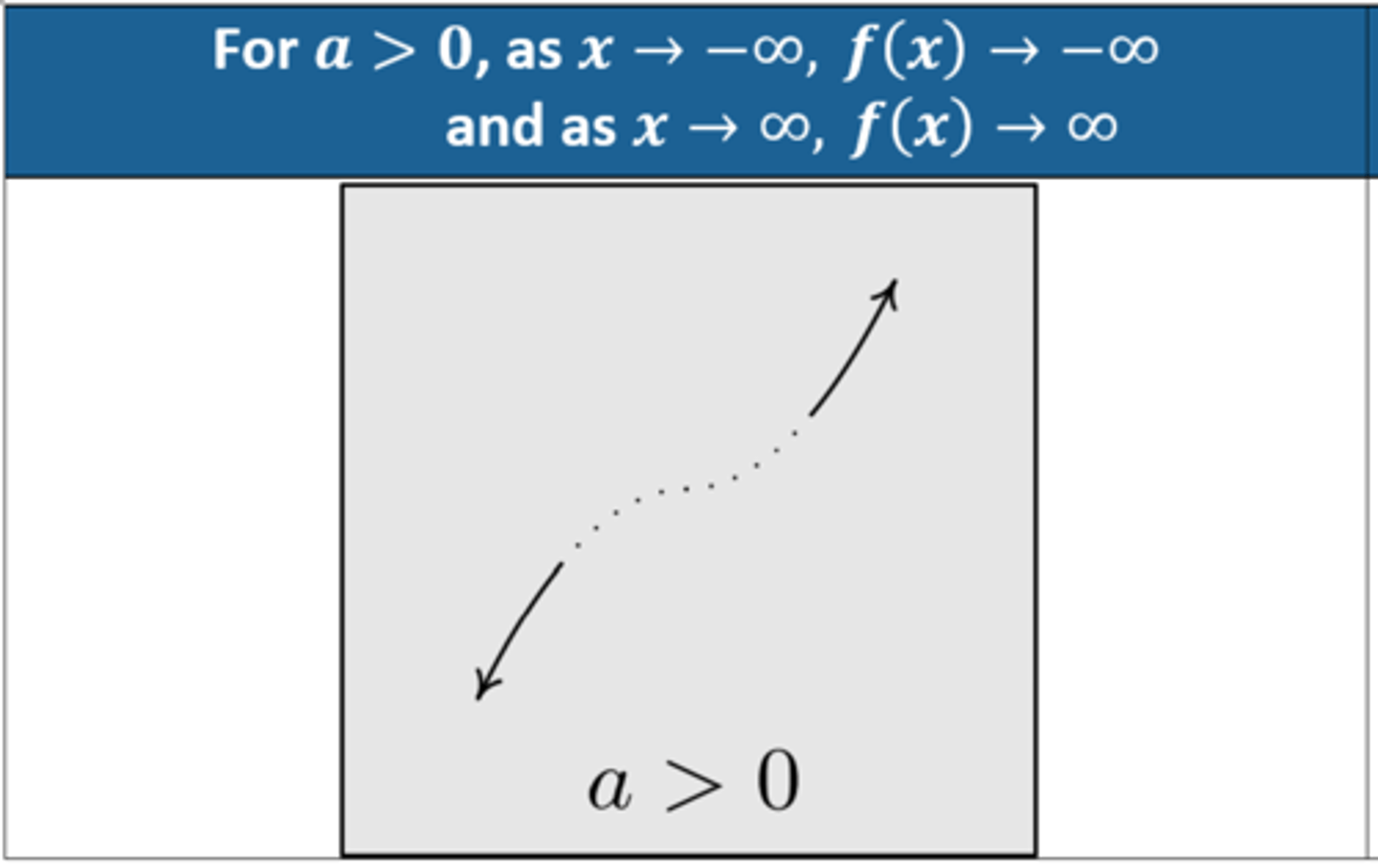
What is the end behavior for the function f(x)=axⁿ, when n is odd and a is negative?

As x→-∞, f(x)→∞ and

as x→∞, f(x)→-∞

The end behavior of a polynomial is completely determined by its ___________.

Leading Term

How do you find the x-intercepts for a polynomial?

Set y=0 and solve for x. Express your answers as points: (a, 0)

How do you find the y-intercept for a polynomial?

Set x=0 and solve for y. Express your answer as a point: (0, b)

What is the behavior of the graph of y=f(x) near a zero with even multiplicity?

The graph touches and rebounds from the x-axis

What is the behavior of the graph of y=f(x) near a zero with odd multiplicity?

The graph crosses through the x-axis

The Intermediate Value Theorem

The graph of a polynomial function (which is always continuous!) cannot be above the x-axis at one point and below the x-axis at another point without crossing the x-axis somewhere in between

How do we construct a sign diagram?

Sign diagrams are used to find where a polynomial function is positive and where it is negative. The steps to construct a sign diagram are:

1. Find the zeros of f and place them on the number line with the number 0 above them.

2. Choose a real number, called a test value, in each of the intervals determined in step 1.

3. Determine the sign of for each test value in step 2, and write that sign above the corresponding interval.

The Factor Theorem

1. If the real number c is a zero of the polynomial then (x-c) is a factor of the polynomial AND

2. If (x-c) is a factor of the polynomial, then c is a zero of the polynomial

Given a polynomial of degree n, the function has __________ distinct real-valued x-intercepts / zeros

at most n

Given a polynomial of degree n, the function has __________ local extrema /"turning points"

at most n-1

The Rational Zeros Theorem

Suppose f(x) is a polynomial with degree n>=1 and integer coefficients.

If r is a rational zero of f,

then r=±p/q where p is a factor of the constant term and q is a factor of the leading coefficient