Math2940 Prelim 2

What is a vector space?

A vector space is a set of vectors that is closed under vector addition and scalar multiplication. It must satisfy the following properties:

• Associativity of Vector Addition: For any vectors u, v, and w in the vector space, (u + v) + w = u + (v + w).

• Associativity of Scalar Multiplication: For any scalars a and b, and any vector u, a(bu) = (ab)u.

• Existence of Zero Vector: There exists a zero vector (0) such that for any vector u, u + 0 = u.

• Existence of Negatives: For each vector u, there exists a vector -u such that u + (-u) = 0.

• Distributivity: For any scalars a and b, and any vector u, a(u + v) = au + av.

• Identity for Scalar Multiplication: For any vector u, 1*u = u

Invertible matrix theorem

a. A is an invertible matrix.

b. A is row equivalent to the n×n identity matrix.

c. A has n pivot positions.

d. The equation Ax = 0 has only the trivial solution.

e. The columns of A form a linearly independent set.

f. The linear transformation x ↦ Ax is one-to-one.

g. The equation Ax = b has at least one solution for each b in ℝⁿ.

h. The columns of A span ℝⁿ.

i. The linear transformation x ↦ Ax maps ℝⁿ onto ℝⁿ.

j. There is an n×n matrix C such that CA = I.

k. There is an n×n matrix D such that AD = I.

l. Aᵀ is an invertible matrix.

Algorithm for finding A^-1

The row reduced form of [A I] is equivalent to [I A^-1 ]

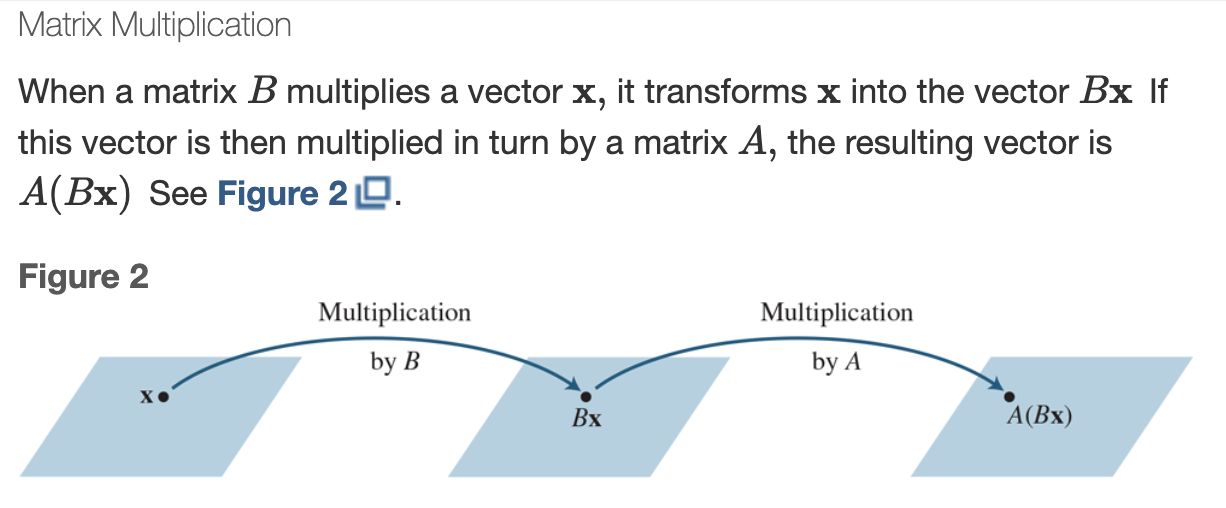
How to multiply matrices

Essentially, if A and B are both matrices then AB is [Ab₀ … Ab_n] where b_0…n is an element of the matrix B.

Rank & Invertible Matrix Theorem

Let A be an n x n matrix. Then the following statements are each equivalent to the statement that A is an invertible matrix:

• The columns of A form a basis of Rⁿ

• ColA = Rⁿ

• rankA = n

• dimNulA = 0

• NulA = {0}

Invertibility criteria in terms of determinants

A square matrix A is invertible iff det(A) ≠ 0

Properties of determinants

Row Operations

• If, in a matrix A, a multiple of one row is added to another row to produce the matrix B then det(A) = det(B)

• If two rows are interchanged in matrix A to produce matrix B, then det(A) = -det(B)

• If one row of A is multiplied by k to produce B then det(B) = k det(A)

if A and B are n by n matrices then: det(AB) = det(A)det(B)

What is a cofactor and what is the sign of a cofactor determined by?

Sign: (-1)^(i+j)

A cofactor is

Geometric interpretation of matrix multiplication & corresponding formula

isomorphism

isomorphisms preserve the relationships between structures, so the algebraic and arithmetic operations are the same and if a mapping is onto and/or one-to-one then it still one-to-one and

Ways of computing determinants

• Row reduction into echelon form: the product of the entries on the main diagonal is the determinant of the matrix, but with a sign change (-1)^r where r is the number of interchanges we did to get it in echelon form.

• Cofactor expansion: uses a recursive formula to compute the determinant by expanding along a row or column.

• Formulas for 2×2 and 3×3 cases:

  • ad-bc

  • For the 3×3 case, there is an attached image

a