1.3 New Functions from Old Fucntions

What would a graph of f(x) = x² look like

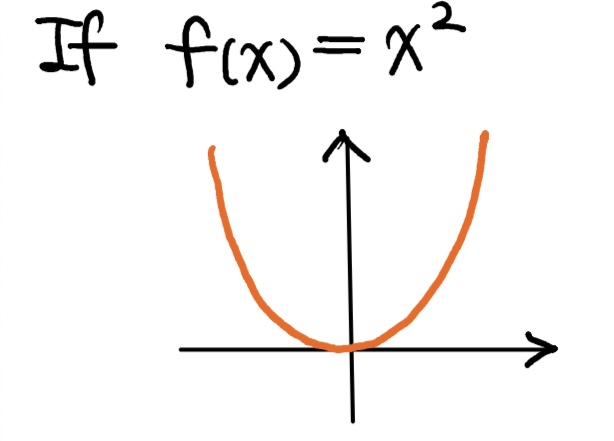
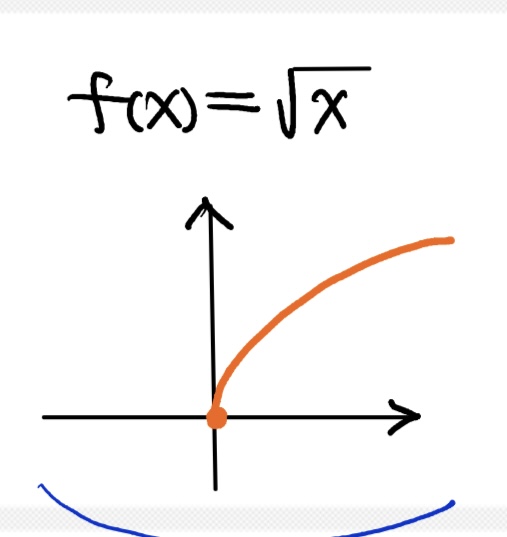
What would a graph of f(x) = √x

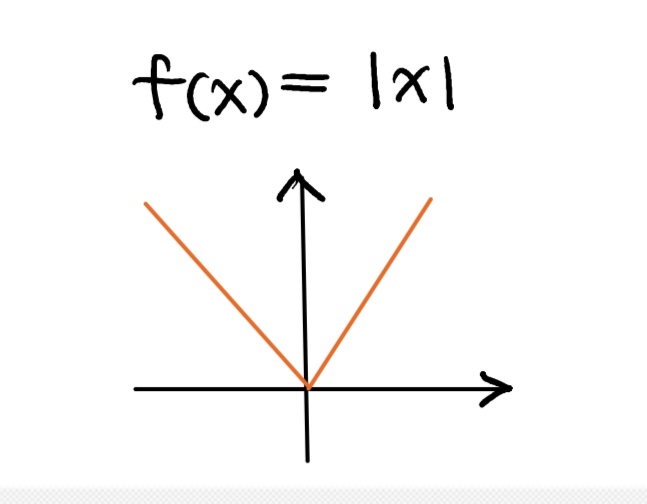
What would the graph of f(x) = | x |

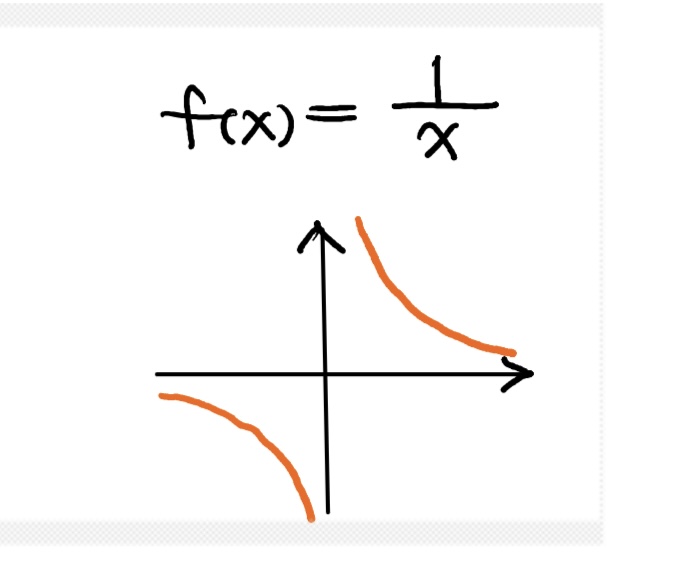
What would a graph of f(x) = 1/x look like

Vertical shifts in graphs

Y= f(x) + c, if c>0, it goes up, if c<0, it goes down

Horizontal shifts in graphs

Y= f(x + c), if c>0, it goes left, if c<0, it goes right

Reflecting

Y= -f(x) then it reflects about the x-axis, y=f(-x) then it reflects about the y-axis

Vertical Stretching

Y= a f(x), if a>1, it’s a vertical stretch —the graph gets taller, if a<1, it’s a vertical compression —the graph gets squashed vertically. To solve you do (x, a x f(x)) meaning the x-values stay the same but the y-value gets multiplied by a

Horizontal Stretching

Y= f(bx), if b>1, its compresses ( squeezes the graph inwards) , if b<1, its stretches (pulls the graph outwards). To solve do ( x/b , f(x))

Steps for sketching a function in the form y = af (bx+c) + d

1)Start with the parent function, 2) Complete Horizontal transformations ( scaling then shifting), 3) Complete Vertical transformations (scaling then shifting)